RBF神经网络案例——客户流失率预测

目录

背景介绍

1、径向基神经网络结构

 2、符号说明

3、计算网络输出

 4、计算能量函数

网络学习步骤

步骤1、先将能量函数E写成各参数的复合函数结构

步骤2、求E关于各参数的偏导

步骤3、求各参数的调整量

步骤4、计算各参数的调整量 

5、按照步骤1-步骤4编写RBF神经网络学习程序

6、网络拟合效果与各个参数的关系

6.1 拟合效果与学习次数的关系

 6.2 拟合效果与隐含层神经元个数的关系

 6.3 学习效率对训练效果的影响

7、添加动量因子的RBF神经网络学习 

---

背景介绍

某消费品女性顾客流失率

周数	流失率	周数	流失率
1	0.531731985	31	0.906074968
2	0.599828865	32	0.910126947
3	0.644564773	33	0.91328894
4	0.671027441	34	0.917005814
5	0.697281167	35	0.920081668
6	0.717013297	36	0.924666569
7	0.732752613	37	0.928067079
8	0.745040151	38	0.932732111
9	0.75565936	39	0.936609264
10	0.763524144	40	0.940518784
11	0.779177473	41	0.94417839
12	0.792189854	42	0.946870779
13	0.806571209	43	0.958960328
14	0.813644571	44	0.961151737
15	0.822233807	45	0.963206107
16	0.826976013	46	0.964973998
17	0.837737352	47	0.967341306
18	0.842773177	48	0.96778647
19	0.854878049	49	0.968232044
20	0.859771055	50	0.970466082
21	0.863536819	51	0.974362934
22	0.865907219	52	0.98011496
23	0.869966906	53	0.98424337
24	0.872734818	54	0.987633062
25	0.875641915	55	0.991046183
26	0.878079332	56	0.995581505
27	0.881514601	57	0.997785861
28	0.886842845	58	1
29	0.891857506	59	1
30	0.898078292	60	1

女性消费商品，品牌的黏性非常重要，但同时商品又是有生命周期的，所以客户群体也会有生命周期，老客户会逐渐流失，新客户不断加入进来，如此便形成了良性客户族新陈代谢。我们需要对客户流失概率进行研究，以便做出一些客户关怀和维系的动作，以减少客户流失，从而使得客户价值最大化。

上表的意义：某女装品牌，假设第一次购买的客户为新客户，则第一周有11865人，只买了第一次而后再未购买的客户为6309人。新增客户表示第一周购买之后在后面数周又购买第二次的人数，不重复计算。

各周损失率计算方法如下：
从未购买的人数/11865=0.531731
从未购买的人数/（11865-1347）=0.599838
…
请用神经网络分析客户任意时间长度没有回头购买的流失率。

1、径向基神经网络结构

径向基神经网络由输入层、隐含层和输出层构成三层前向网络，隐含层采用径向基函数为激励函数（一般是高斯函数）。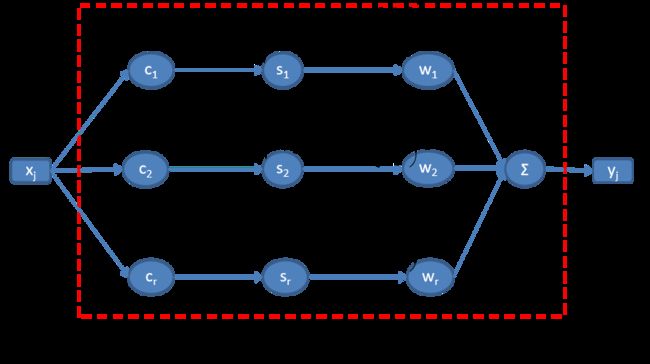

 2、符号说明

• 样本输入,容量为n;
• 样本输出；
• r   隐含层的神经元个数；
• 第i个神经元的中心和宽度;i=1,2,…,r；
• wi   第i个神经元的权值,i=1,2,…,r;

3、计算网络输出

 设神经网络输入和输出都是线性的，则整个隐含层的输入就是样本输入，隐含层的输出也是样本输出，因此(对第j个样本的)为j=1,2,…,n；

 4、计算能量函数

用最小二乘法，拟合参数ci,σi,wi的最佳值。

网络学习步骤

步骤1、先将能量函数E写成各参数的复合函数结构

步骤2、求E关于各参数的偏导

i=1,2,…,r 

步骤3、求各参数的调整量

为了计算方便，先规范样本输入和输出都是行向量(n)，权值、中心和宽度向量w,c,σ都是列向量(r)，则e=(yj-Oj)为n维行向量，dji=(xj-ci)为n×r矩阵,(pji)=p(xj,ci,σi)也是n×r矩阵。则各参数调整量（按负梯度方向进行）为

步骤4、计算各参数的调整量 

 i=1,2,…,r

其中lrw,lrc,lrσ表示相应参数的学习进度（速度）。

5、按照步骤1-步骤4编写RBF神经网络学习程序

function [o,eb,s1]=BRF(X,Y,lrw,lrc,lrs,sig,r,n)
x=mapminmax(X);
[y,s1]=mapminmax(Y);
m=length(y);
w=rand(r,1)+0.1;
c=rand(r,1);
s=rand(r,1)+0.2;
eb=[];
for k=1:n
    d1=dist(c,x);
    d2=d1.^2;
    ss=[];
    for i=1:r
        sr=ones(1,m)*s(i)^2;
        ss=[ss;sr];
    end
    p=exp(-d2./ss);
    o=[];
    for j=1:m
       for i=1:r
           wp(i)=w(i)*p(i,j);
       end
       o=[o,sum(wp)];
    end
    e=y-o;
    err=sum(e.^2)^0.5;
    if err

6、网络拟合效果与各个参数的关系

6.1 拟合效果与学习次数的关系

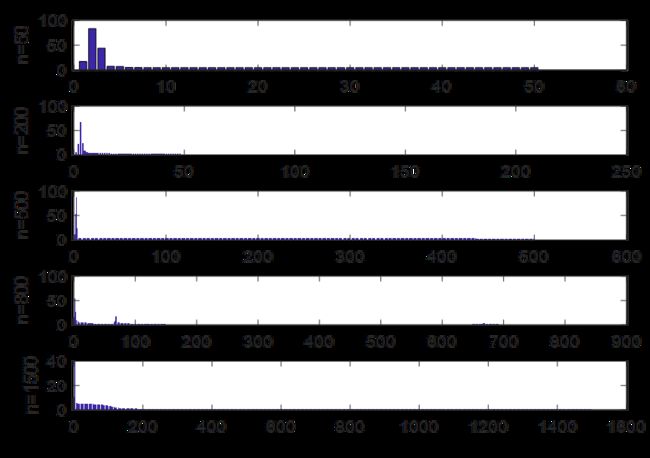
 取定权学习效率为lrw=0.035,中心权值学习lrc =0.01,宽度学习效率为lrs=0.01,神经元个数r=8，残差容量sig=0.001，分别对练习次数n=50，200，500，800，1500残差效果进行对比，结果如图，程序见下

clear
A=xlsread('d:\kehu.xlsx');
Y=A';
X=1:60;
t=1:length(X);
r=8;sig=0.001;lrw=0.035;lrc=0.01;lrs=0.01;
n=50;
[o,eb1,s1]=BRF(X,Y,lrw,lrc,lrs,sig,r,n);
subplot(5,1,1);
bar(eb1);
n=200;
[o,eb2,s1]=BRF(X,Y,lrw,lrc,lrs,sig,r,n);
subplot(5,1,2);
bar(eb2);
n=500;
[o,eb3,s1]=BRF(X,Y,lrw,lrc,lrs,sig,r,n);
subplot(5,1,3);
bar(eb3);
n=800;
[o,eb4,s1]=BRF(X,Y,lrw,lrc,lrs,sig,r,n);
subplot(5,1,4);
bar(eb4);
n=1500;
[o,eb5,s1]=BRF(X,Y,lrw,lrc,lrs,sig,r,n);
subplot(5,1,5);
bar(eb5);

clear
A=xlsread('d:\kehu.xlsx');
Y=A';
X=1:60;
t=1:length(X);arf=0.002;n=1500;
r=10;sig=0.003;lrw=0.0035;lrc=0.0035;lrs=0.0035;

 6.2 拟合效果与隐含层神经元个数的关系

取定权学习效率为lrw=0.035,中心学习lrc=0.01,宽度学习效率为lrs=0.01,残差容量sig=0.001，学习次数定为n=800，分别隐含层神经元数r=4,8,12,16效果进行对比，结果如图，程序见下

clear
A=xlsread('d:\kehu.xlsx');
Y=A';
X=1:60;n=600;
t=1:length(X);
sig=0.001;lrw=0.035;lrc=0.01;lrs=0.01;
[o,eb1,s1]=BRF(X,Y,lrw,lrc,lrs,sig,4,n);
[o2,eb2,s2]=BRF(X,Y,lrw,lrc,lrs,sig,8,n);
[o3,eb3,s3]=BRF(X,Y,lrw,lrc,lrs,sig,12,n);
[o4,eb4,s4]=BRF(X,Y,lrw,lrc,lrs,sig,14,n);
ebmax=max(eb1);
eb2=eb2(eb2<=ebmax);
eb3=eb3(eb3<=ebmax);
eb4=eb4(eb4<=ebmax);
subplot(2,2,1),bar(eb1);
subplot(2,2,2),bar(eb2);
subplot(2,2,3),bar(eb3);
subplot(2,2,4),bar(eb4);

                                                        学习效果与神经元数关系

 由图可以看出：

1、r较小时，残差震荡厉害，但误相对较小；

2、r较大时，残差震荡不大，但收敛慢。

 6.3 学习效率对训练效果的影响

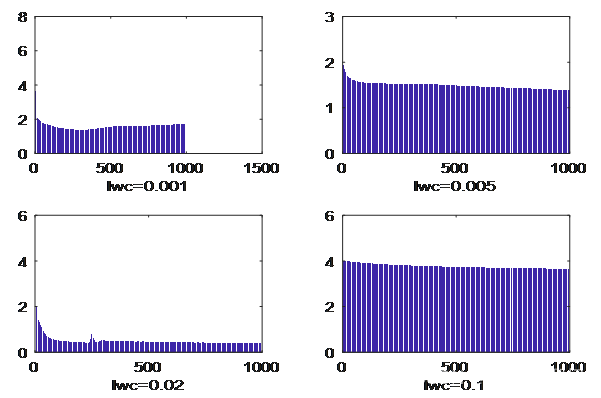
取定中心学习lrc=0.01,宽度学习效率为lrs=0.01,残差容量sig=0.001，学习次数定为n=1000，隐含层神经元数r=8。让权学习效率分别取lrw=0.001,0.005,0.02,0.08,将效果进行对如图.

clear
A=xlsread('d:\kehu.xlsx');
Y=A';
X=1:60;n=1000;
t=1:length(X);
sig=0.001;r=8;lrc=0.01;lrs=0.01;
[o1,eb1,s1]=BRF(X,Y,0.001,lrc,lrs,sig,r,n);
[o2,eb2,s2]=BRF(X,Y,0.005,lrc,lrs,sig,r,n);
[o3,eb3,s3]=BRF(X,Y,0.02,lrc,lrs,sig,r,n);
[o4,eb4,s4]=BRF(X,Y,0.1,lrc,lrs,sig,r,n);
ebmax=max(eb1);
eb2=eb2(eb2<=ebmax);
eb3=eb3(eb3<=ebmax);
eb4=eb4(eb4<=ebmax);
subplot(2,2,1),bar(eb1);
subplot(2,2,2),bar(eb2);
subplot(2,2,3),bar(eb3);
subplot(2,2,4),bar(eb4);

                                                不同权学习效率效果对比

由图可以看出，权值过于小和过于大，学习效果都不太理想，lrw=0.02学习效果最好。

取定权学习效率lrw=0.02,宽度学习效率为lrs=0.01,残差容量sig=0.001，学习次数定为n=1000，隐含层神经元数r=8。让中心学习效率分别取lrw=0.001,0.005,0.02,0.08,将效果进行对如图

clear
A=xlsread('d:\kehu.xlsx');
Y=A';
X=1:60;n=1000;
t=1:length(X);
sig=0.001;r=8;lrw=0.02;lrs=0.01;
[o1,eb1,s1]=BRF(X,Y,lrw,0.001,lrs,sig,r,n);
[o2,eb2,s2]=BRF(X,Y,lrw,0.005,lrs,sig,r,n);
[o3,eb3,s3]=BRF(X,Y,lrw,0.02,lrs,sig,r,n);
[o4,eb4,s4]=BRF(X,Y,lrw,0.1,lrs,sig,r,n);
ebmax=max(eb1);
eb2=eb2(eb2<=ebmax);
eb3=eb3(eb3<=ebmax);
eb4=eb4(eb4<=ebmax);
subplot(2,2,1),bar(eb1);
subplot(2,2,2),bar(eb2);
subplot(2,2,3),bar(eb3);
subplot(2,2,4),bar(eb4);

                                               中心学习效率与学习效果关系对比 

由图可以看出，当其他参数不变时，中心学习效率不能太小，也不能太大，给出的四个值中lrc=0.005时学习效果最佳。

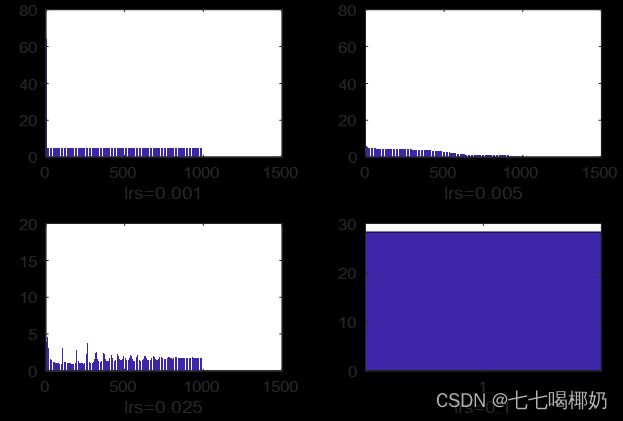
 取定权学习效率lrw=0.02,中心学习效率为lrc=0.005,残差容量sig=0.001，学习次数定为n=1000，隐含层神经元数r=8。让宽度学习效率分别取lrs=0.001,0.005,0.025,0.1,将效果进行对如图

clear
A=xlsread('d:\kehu.xlsx');
Y=A';
X=1:60;n=1000;
t=1:length(X);
sig=0.001;r=8;lrw=0.02;lrc=0.005;
[o1,eb1,s1]=BRF(X,Y,lrw,lrc,0.001,sig,r,n);
[o2,eb2,s2]=BRF(X,Y,lrw,lrc,0.005,sig,r,n);
[o3,eb3,s3]=BRF(X,Y,lrw,lrc,0.025,sig,r,n);
[o4,eb4,s4]=BRF(X,Y,lrw,lrc,0.1,sig,r,n);
ebmax=max(eb1);
eb2=eb2(eb2<=ebmax);
eb3=eb3(eb3<=ebmax);
eb4=eb4(eb4<=ebmax);
subplot(2,2,1),bar(eb1);
subplot(2,2,2),bar(eb2);
subplot(2,2,3),bar(eb3);
subplot(2,2,4),bar(eb4);

                                                宽度学习效率对残差影响

  由图(8)可以看出，不同宽度学习效率对残差影响较大，给出的四个值中，lrs=0.005的网络学习效果最好。

给定r=8,n=20000,lrw=0.02,lrc=0.005,lrs=0.005，sig=0.001，对网络进行深度训练，训练效果如图 

clear
A=xlsread('d:\kehu.xlsx');
Y=A';
X=1:60;n=20000;
t=1:length(X);
sig=0.001;r=8;lrw=0.02;lrc=0.005;lrs=0.005;
[o1,eb1,s1]=BRF(X,Y,lrw,lrc,lrs,sig,r,n);
t=1:length(Y);
y=mapminmax('reverse',o1,s1);
subplot(2,1,1);
plot(t,Y,'*',t,y,'+-');legend('ʵ¼ÊÖµ','Ô¤²âÖµ');
subplot(2,1,2);
eb1=eb1(eb1<10);
bar(eb1);

                                                        最佳学习效率的学习效果 

7、添加动量因子的RBF神经网络学习 

由前面的计算可知，当学习时间短，参数取得稍微不恰当，网络学习为出现两个严重问题：

（1） 残差震荡现象严重；

（2）收敛速度慢。

对于（2）可以增加学习时间，而对于（1），震荡现象不尽早消除，会陷入局部极值，普遍做法是在负梯度方向加入干扰因子，称为动量因子。新的参数公式如下i=1,2,…,r

其中，fw,fc,fσ分别为权、中心、宽度的动量因子系数，Δw-1是权的动量因子，-1的意思，把上一次的调整方向当作这次的动量方向。关于c和s的解释一样。

利用前面找到的个最佳参数，添加动量因子编制一个RBF神经网络学习程序

function [o,eb,s1]=BRFr(X,Y,lrw,lrc,lrs,fw,fc,fs,sig,r,n)
x=mapminmax(X);
[y,s1]=mapminmax(Y);
m=length(y);
w=rand(r,1);
c=2*rand(r,1)-1;
s=rand(r,1)+0.1;
eb=[];
wr=zeros(r,1);
cr=wr;
sr=wr;

for k=1:n
    d1=dist(c,x);
    d2=d1.^2;
    ss=[];
    for i=1:r
        sr1=ones(1,m)*s(i)^2;
        ss=[ss;sr1];
    end
    p=exp(-d2./ss);
    o=[];
    for j=1:m
       for i=1:r
           wp(i)=w(i)*p(i,j);
       end
       o=[o,sum(wp)];
    end
    e=y-o;
    err=sum(e.^2)^0.5;
    if err

利用前面找到的个最佳参数，添加动量因子编制一个RBF神经网络学习程序

clear
A=xlsread('d:\kehu.xlsx');
Y=A';
X=1:60;n=1000;
t=1:length(X);
sig=0.001;r=8;lrw=0.02;lrc=0.005;lrs=0.005;
fc=0.001;fw=0.01;fs=0.001;
[o1,eb1,s1]=BRFr(X,Y,lrw,lrc,lrs,fw,fc,fs,sig,r,n);
t=1:length(Y);
y=mapminmax('reverse',o1,s1);
subplot(2,1,1);
plot(t,Y,'*',t,y,'+-');legend('ʵ¼ÊÖµ','Ô¤²âÖµ');
subplot(2,1,2);
eb1=eb1(eb1<10);
bar(eb1);

                                加入动量因子的学习效果

由参数n=1000计算效果得出如下结论：

（1）学习时间短；

（2）残差震荡先现象不明显；

（3）收敛的一致性较好。