【C++】leetcode力扣 剑指 Offer 题解

力扣链接

剑指 Offer 03. 数组中重复的数字

法一：暴力解法
使用两层循环，超时

class Solution {
public:
    int findRepeatNumber(vector<int>& nums) {
        
        for(int i=0;i<nums.size();i++){
            for(int j=i+1;j<nums.size();j++){
                if(nums[j]==nums[i]){
                    return nums[i];
                }
            }
        }
    return 0;
    }
};

法二：使用unordered_map计数

class Solution {
public:
    int findRepeatNumber(vector<int>& nums) {
        unordered_map<int,int> m;

        for(int i=0;i<nums.size();i++){
            if(m.find(nums[i])!=m.end()){//如果存在说明出现重复的
                return nums[i];
            }
            m[nums[i]]++;//记录每个数字出现的次数
        }
        
    return -1;
    }
};

剑指 Offer 04. 二维数组中的查找

class Solution {
public:
    bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
        
        int max_x=matrix.size();//二维数组行数
        if(max_x==0) return false;//注意特殊情况的判断
        int max_y=matrix[0].size();//二维数组列数
        for(int i=0;i<max_x;i++){
            for(int j=0;j<max_y;j++){
                if(matrix[i][j]>target){//说明第j列之后的列（包括第j列）都大于target
                    max_y=j;//更新能到达的最大列
                }
                else if(matrix[i][j]==target){
                    return true;
                }
                else continue;//小于，继续遍历
            }
        }
        return false;
    }
};

剑指 Offer 05. 替换空格

法一：创建新字符串result存放

class Solution {
public:
    string replaceSpace(string s) {
        string result="";
        for(char c:s){
            if(c==' '){
                result+="%20";
            }
            else{
                result+=c;
            }
        }
        return result;
    }
};

法二：使用双指针原地操作

class Solution {
public:
    string replaceSpace(string s) {
        //双指针
        int cout=0;
        for(char c:s){
            if(c==' ') cout++;
        }
        int i=s.size()-1;
        s.resize(s.size()+2*cout);
        int j=s.size()-1;
        for(i,j;i>=0;i--){
            if(s[i]==' '){
                s[j]='0';
                s[j-1]='2';
                s[j-2]='%';
                j=j-3;
            }
            else{
                s[j--]=s[i];
            }
        }
        return s;
    }
};

剑指 Offer 06. 从尾到头打印链表

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> reversePrint(ListNode* head) {
        vector<int> result;
        while(head){
            result.push_back(head->val);
            head=head->next;
        }
        for(int i=0,j=result.size()-1;i<j;i++,j--){//使用双指针反转数组
            swap(result[i],result[j]);
        }
        return result;
    }
};

剑指 Offer 07. 重建二叉树

题目给了双向链表节点的结构体
采用递归思想来写代码，每次递归传入的前序遍历和中序遍历的数组都是去掉的head节点之后的左子树的前序遍历和中序遍历数组、右子树的前序遍历和中序遍历数组

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if(preorder.size()==0) return NULL;

        TreeNode* head=new TreeNode(preorder[0]);//前序遍历的第一个值就是根节点val值

        vector<int> left_inorder;//head节点的左子树的中序遍历结果
        vector<int> right_inorder;//head节点的右子树的中序遍历结果
        int i=0;
        for(;i<inorder.size();i++){
            if(inorder[i]==preorder[0]) break;
            left_inorder.push_back(inorder[i]);
        }
        i++;//记得加一跳过根节点，因为break不会执行i++
        for(;i<inorder.size();i++){
            right_inorder.push_back(inorder[i]);
        }

        vector<int> left_pre;//head节点的左子树的前序遍历结果
        vector<int> right_pre;//head节点的右子树的前序遍历结果
        int j=1;
        for(;j<1+left_inorder.size();j++){
            left_pre.push_back(preorder[j]);
        }
        for(;j<preorder.size();j++){
            right_pre.push_back(preorder[j]);
        }

        head->left=buildTree(left_pre,left_inorder);
        head->right=buildTree(right_pre,right_inorder);

        return head;
    }
};

剑指 Offer 09. 用两个栈实现队列

class CQueue {
public:
    stack<int> st;//存放和队列顺序一样的值
    stack<int> temp;//中转栈
    CQueue() {
        
    }
    
    void appendTail(int value) {//队列尾部插入整数
      
        while(!st.empty()){
            int val=st.top();
            st.pop();
            temp.push(val);
        }
        temp.push(value);
        while(!temp.empty()){
            int val=temp.top();
            temp.pop();
            st.push(val);
        }
    }
    
    int deleteHead() {//队列头部删除整数
        if(st.size()==0) return -1;
        int val=st.top();
        st.pop();
        return val;
    }
};


/**
 * Your CQueue object will be instantiated and called as such:
 * CQueue* obj = new CQueue();
 * obj->appendTail(value);
 * int param_2 = obj->deleteHead();
 */

剑指 Offer 10- I. 斐波那契数列

使用动态规划
注意在循环里面每一步的结果都应该取模后再进行赋值，而不应该最后return的时候再取模，会溢出

class Solution {
public:
    int fib(int n) {
        if(n==0) return 0;
        vector<int> dp(n+1,0);
        dp[0]=0;dp[1]=1;
        for(int i=2;i<dp.size();i++){
            dp[i]=(dp[i-1]+dp[i-2])%1000000007;
        }
        return dp[n];
    }
};

剑指 Offer 10- II. 青蛙跳台阶问题

class Solution {
public:
    int numWays(int n) {
        if(n==0) return 1;
        vector<int> dp(n+1,0);
        dp[0]=1;
        dp[1]=1;
        for(int i=2;i<dp.size();i++){
            dp[i]=(dp[i-1]+dp[i-2])%1000000007;
        }
        return dp[n];
    }
};

剑指 Offer 11. 旋转数组的最小数字

法一：
一开始想的是对数组进行排序，利用sort函数返回第一个元素,以为会超时，结果没有

class Solution {
public:
    int minArray(vector<int>& numbers) {
        sort(numbers.begin(),numbers.end());
        return numbers[0];
    }
};

法二：对法一优化一下，循环查找，直到找到第一个比前一个数小的就返回

class Solution {
public:
    int minArray(vector<int>& numbers) {
        int num=numbers[0];
        for(int i=1;i<numbers.size();i++){
            if(numbers[i]<numbers[i-1]){
                num=numbers[i];
                break;
            }
        }
        return num;
    }
};

剑指 Offer 12. 矩阵中的路径

第一遍写的代码是有问题的
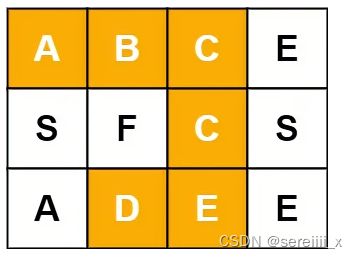
比如word="SEE"时
代码相当于只考虑了一种情况，S找到上面E后继续循环，然后返回false，这样是有问题的，其实下面的E完全没考虑到

class Solution {
public:
    bool is_true(vector<vector<char>>& board,string word,int index_i,int index_j){
        //i,j是word第一个字母在board中的位置
        int m=board.size();
        int n=board[0].size();
        vector<vector<bool>> is_used(m,vector<bool>(n,false));//判断某个位置是否已经使用过了，false代表没使用
        for(int i=1;i<word.size();i++){
            //判断上下左右的位置是否有符合要求的
            //上面
            if(index_i-1>=0&&is_used[index_i-1][index_j]==false&&board[index_i-1][index_j]==word[i]){//不能超限&&上方格子未使用
                    is_used[index_i-1][index_j]=true;
                    index_i--;
                    continue;
            }
            //下面
            if(index_i+1<m&&is_used[index_i+1][index_j]==false&&board[index_i+1][index_j]==word[i]){//不能超限&&下方格子未使用
                    is_used[index_i+1][index_j]=true;
                    index_i++;
                    
                    continue;
            } 
            //左边
            if(index_j-1>=0&&is_used[index_i][index_j-1]==false&&board[index_i][index_j-1]==word[i]){//不能超限&&左边格子未使用
                    index_j--;
                    is_used[index_i][index_j]=true;
                    continue;
            
            } 
            //右边
            if(index_j+1<n&&is_used[index_i][index_j+1]==false&&board[index_i][index_j+1]==word[i]){//不能超限&&右边格子未使用
      
                    index_j++;
                    is_used[index_i][index_j]=true;
                    continue;
            
            }
            return false;//四个格子都不符合
        
        }
        return true;
    }
    bool exist(vector<vector<char>>& board, string word) {
        for(int i=0;i<board.size();i++){
            for(int j=0;j<board[0].size();j++){
                if(board[i][j]==word[0]){
                    bool label=is_true(board,word,i,j);
                    if(label) return true;
                    else continue;
                }
            }
        }
        return false;
    }
};

改正后：使用递归进行改正
dfs经典例子

class Solution {
public:

    bool is_true(vector<vector<char>>& board,string word,int index,int index_i,int index_j,vector<vector<bool>> &is_used){
        //index_i,index_j是index-1位置的字母在board中的位置
        //index是word中本次要比较的下标
        if(index==word.size()) return true;//说明前面的字母都符合要求，返回true

        int m=board.size();
        int n=board[0].size();
        bool label1=false;
        bool label2=false;
        bool label3=false;
        bool label4=false;

        //搜索上下左右的位置是否有=word[index]的
        //上面
        if(index_i-1>=0&&is_used[index_i-1][index_j]==false&&board[index_i-1][index_j]==word[index]){//不能超限&&上方格子未使用
            is_used[index_i-1][index_j]=true;
            label1=is_true(board,word,index+1,index_i-1,index_j,is_used);
            is_used[index_i-1][index_j]=false;
                 
        }
        //下面
        if(index_i+1<m&&is_used[index_i+1][index_j]==false&&board[index_i+1][index_j]==word[index]){//不能超限&&下方格子未使用
            is_used[index_i+1][index_j]=true;
            label2=is_true(board,word,index+1,index_i+1,index_j,is_used);
            is_used[index_i+1][index_j]=false;    
                  
        } 
        //左边
        if(index_j-1>=0&&is_used[index_i][index_j-1]==false&&board[index_i][index_j-1]==word[index]){//不能超限&&左边格子未使用      
            is_used[index_i][index_j-1]=true;
            label3=is_true(board,word,index+1,index_i,index_j-1,is_used);
            is_used[index_i][index_j-1]=false;                      
        } 
        //右边
        if(index_j+1<n&&is_used[index_i][index_j+1]==false&&board[index_i][index_j+1]==word[index]){//不能超限&&右边格子未使用          
            is_used[index_i][index_j+1]=true;
            label4=is_true(board,word,index+1,index_i,index_j+1,is_used);
            is_used[index_i][index_j+1]=false;                        
        }
           
        bool label=label1||label2||label3||label4;//只要有一个方向找到了就可以
        return label;
    }
    bool exist(vector<vector<char>>& board, string word) {
        int m=board.size();
        int n=board[0].size();
        vector<vector<bool>> is_used(m,vector<bool>(n,false));//判断某个位置是否已经使用过了，false代表没使用
        for(int i=0;i<board.size();i++){
            for(int j=0;j<board[0].size();j++){
                if(board[i][j]==word[0]){
                    is_used[i][j]=true;
                    //根据is_true函数参数的定义，这里必须要先对word[0]进行判断后才可以调用这个递归函数
                    bool label=is_true(board,word,1,i,j,is_used);
                    is_used[i][j]=false;
                    if(label) return true;                    
                }

            }
        }
        return false;
    }
};

剑指 Offer 13. 机器人的运动范围

这道题如果这样思考就是错误的：直接两层for循环嵌套判断每个格子的数位之和是否大于k
其实有些格子数位之和大于k之后它就成了障碍物，比如m=16，n=8，k=4，期望输出是15，（10，0）数位之和小于4，看似符合要求，其实并不符合要求，因为前面某些行整行都是障碍物，根本没办法到达（10，0）这个点

正确做法如下：使用深度优先搜索dfs算法

class Solution {
public:
    int sum=1;//[0,0]位置肯定是符合的
    void dfs(int m, int n, int k,vector<vector<bool>> &is_used,int index_i,int index_j){
        //index_i,index_j是当前要搜索的位置
        //向上走
        if(index_i-1>=0&&is_used[index_i-1][index_j]==false){
            if((index_i-1)/10+(index_i-1)%10+index_j/10+index_j%10<=k){
                sum++;
                is_used[index_i-1][index_j]=true;
                dfs(m,n,k,is_used,index_i-1,index_j);

                //注意这道题并不需要回溯，因为能运行到这里都是符合要求的方格，需要计算出所有符合要求的方格
                // is_used[index_i-1][index_j]=false;
                // sum--;
            }
            
        }
        //向下走
        if(index_i+1<m&&is_used[index_i+1][index_j]==false){
            if((index_i+1)/10+(index_i+1)%10+index_j/10+index_j%10<=k){//说明下面的格子符合要求
                sum++;
                is_used[index_i+1][index_j]=true;
                dfs(m,n,k,is_used,index_i+1,index_j);

            }
            
        }
        //向左走
        if(index_j-1>=0&&is_used[index_i][index_j-1]==false){
            if(index_i/10+index_i%10+(index_j-1)/10+(index_j-1)%10<=k){
                sum++;
                is_used[index_i][index_j-1]=true;
                dfs(m,n,k,is_used,index_i,index_j-1);

            }
            
        }
        //向右走
        if(index_j+1<n&&is_used[index_i][index_j+1]==false){
            if(index_i/10+index_i%10+(index_j+1)/10+(index_j+1)%10<=k){
                sum++;
                is_used[index_i][index_j+1]=true;
                dfs(m,n,k,is_used,index_i,index_j+1);

            }
            
        }
    }
    int movingCount(int m, int n, int k) {

        vector<vector<bool>> is_used(m,vector<bool>(n,false));
        is_used[0][0]=true;
        dfs(m,n,k,is_used,0,0);
        return sum;
    }
};

剑指 Offer 14- I. 剪绳子

class Solution {
public:
    int cuttingRope(int n) {
        //dp[i]:拆分正整数i（至少分成两段），能得到的最大乘积
        //(i-j)*j相当于是把i分为两个数，而dp[i-j]*j相当于是把i拆分成三个数及以上，因为dp拆分个数>=2     
        vector<int> dp(n+1,1);
        for(int i=2;i<=n;i++){
            for(int j=i-1;j>=1;j--){
                dp[i]=max(j*(i-j),max(dp[i],dp[i-j]*j));
            }
            
        }
        return dp[n];

    }
};

剑指 Offer 15. 二进制中1的个数

class Solution {
public:
    int hammingWeight(uint32_t n) {
        int sum=0;
        while(n){
            if(n%2==1){//判断最末尾的数是否为1
                sum++;
            }
            n=n/2;//左移一位
        }
        return sum;
    }
};

剑指 Offer 16. 数值的整数次方

使用快速幂算法
快速幂算法介绍
代码如下：
核心思想：利用二进制来加快运算

class Solution {
public:
    double myPow(double x, int n) {
        //快速幂算法
        if( n == 0) return 1;
        if( x == 0.0) return 0;
        long  exp = n;//
        if(n < 0) {
            //int的取值范围：-2147483648～2147483647
            exp = n* (-1.0);
            //当n == INT_MIN时正数时大于INT_MAX的，所以要用一个大于 INT_MAX的类型来保存，同时在将他转正的时候， n*(-1)的结果依然是一个 int，此时的int是个隐藏类型，然后才将这个结果赋值给 exp，所以用来保存结果值的不应该是个int型，我们用double型的 -1 ,这样就可以将相乘的结果值保存为一个 double类型了，然后再进行赋值
        } 
        
        double res = 1.0;
        while(exp != 0){
            if( (exp &1) == 1 ){//指数为奇数，exp & 1这相当于exp % 2 == 1
            //如果二进制位是0的话相当于乘上1，可以不用管
                res *=x;
            }
            x *=x;//2^0,2^1,2^2,2^4....
            exp >>= 1;//右移一位，相当于除以2
            //一次的右移将舍弃一个位例如1011(2)一次左移后变成101(2)
        }

        return n<0 ? 1/res: res;
    }
};

剑指 Offer 17. 打印从1到最大的n位数

class Solution {
public:
    vector<int> printNumbers(int n) {
        
        int num=1;
        for(int i=0;i<n;i++){
            num*=10;//计算出最大的n位数+1的值
        }
        vector<int> result(num-1,0);
        for(int i=1;i<num;i++){
            result[i-1]=i;
        }
        return result;
    }
};

剑指 Offer 18. 删除链表的节点

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* deleteNode(ListNode* head, int val) {
        ListNode* virtul_head=new ListNode(0);
        virtul_head->next=head;//虚拟头节点
        ListNode* temp=head;
        ListNode* pre=virtul_head;//前一个节点
        while(temp){
            if(temp->val==val){
                pre->next=temp->next;
                break;
            }
            //更新前一个节点和当前节点
            pre=temp;
            temp=temp->next;
        }
        return virtul_head->next;
    }
};

剑指 Offer 20. 表示数值的字符串

感觉在做这道题的时候就是在面向用例编程，要考虑的情况很多

class Solution {
public:
    bool isNumber(string s) {
        //出现其他字母为false
        int j=0;
        while(s[j]==' '){
            j++;
        }

        //跳过小数和整数的符号位
        if(s[j]=='+'||s[j]=='-'){
            j++;
        }
        int i=j;

        if(i==s.size()) return false;

        //处理小数和整数，保证i指向小数或者整数的第一个数字的位置
        if(s[i]=='.'){
            if(i==s.size()-1) return false;
            //小数点前面是至少一位数字
            int index=i;
            while(i+1<s.size()&&s[i+1]<='9'&&s[i+1]>='0') i++;//跳到后面跟着的数字的位置
            if(index==i) return false;//后面跟着0个数字
        }
        else if(s[i]<='9'&&s[i]>='0'){
            if(i==s.size()-1) return true;
            while(i+1<s.size()&&s[i+1]<='9'&&s[i+1]>='0') i++;//跳到后面跟着的数字位置            
            if(i+1<s.size()&&s[i+1]=='.'){
                i++;
                i++;//跳到小数点后面的一位
                
            }
        }

        //跳过i位置开始的数字
        while((i<s.size()&&s[i]<='9'&&s[i]>='0')){
            i++;
        }
        if(i==s.size()) return true;//说明只有小数或整数
        if(i==j) return false;//说明没有小数或整数（必选）
        if(s[i]=='e'||s[i]=='E'){
            i++;
            if(i==s.size()) return false;
            if(s[i]=='+'||s[i]=='-'){
                i++;
                if(i==s.size()) return false;//说明符号位后面没有跟数字 
            }
            int temp=i;           
            while(i<s.size()&&s[i]<='9'&&s[i]>='0'){
                i++;
            }
            if(i==s.size()) return true;
           if(i==temp) return false;//说明后面没有数字
        }
        while(s[i]==' '){//后面跟着的空格
            i++;
        }
        if(i==s.size()) return true;//说明都是空格
        else return false;
        
    }
};

剑指 Offer 21. 调整数组顺序使奇数位于偶数前面

设计一个新数组和双指针来存放奇偶数

class Solution {
public:
    vector<int> exchange(vector<int>& nums) {
        if(nums.size()<=1) return nums;
        vector<int> result(nums.size(),0);
        int slow=0;
        int fast=nums.size()-1;
        for(int i=0;i<nums.size();i++){
            if(nums[i]%2==1){//奇数
                result[slow++]=nums[i];
            }
            else{
                result[fast--]=nums[i];
            }
        }
        return result;
    }
};

剑指 Offer 22. 链表中倒数第k个节点

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* getKthFromEnd(ListNode* head, int k) {
        int size=1;//节点个数
        ListNode* temp=head;
        while(temp->next){
            temp=temp->next;
            size++;
        }
        temp=head;
        int path=size-k;//需要走的步数
        while(path--){
            temp=temp->next;
        }
        return temp;
    }
};

剑指 Offer 24. 反转链表

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* pre=NULL;
        while(head){//两两交换
            ListNode* next=head->next;
            head->next=pre;
            pre=head;
            head=next;
        }
        return pre;
    }
};

剑指 Offer 25. 合并两个排序的链表

建立新链表，两两比较节点值

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        ListNode* virtual_head=new ListNode(0);
        ListNode* temp=virtual_head;
        while(l1&&l2){
            ListNode* node=new ListNode(0);
            if(l1->val<=l2->val){
                node->val=l1->val;
                l1=l1->next;
                
            }
            else{
                node->val=l2->val;
                l2=l2->next;

            }
            temp->next=node;
            temp=temp->next;
        }
        if(l1){
            temp->next=l1;
        }
        if(l2){
            temp->next=l2;
        }
        return virtual_head->next;
    }
};

剑指 Offer 26. 树的子结构

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool is_true(TreeNode* A, TreeNode* B){
        //使用递归判断树的结构是否相等
        if(B==NULL) return true;
        if(A==NULL) return false;
        if(A->val!=B->val) return false;
        bool left=false;
        bool right=false;
        left=is_true(A->left,B->left);
        right=is_true(A->right,B->right);
        return left&&right;//左右子树结构都相等才是true

    }
    bool isSubStructure(TreeNode* A, TreeNode* B) {
        //使用层次遍历法判断每一个节点的值是否和B的根节点的值相等
        //如果相等就执行判断函数
        if(A==NULL||B==NULL) return false;
        queue<TreeNode*> que;
        que.push(A);
        while(!que.empty()){
            int size=que.size();
            for(int i=0;i<size;i++){
                TreeNode* node=que.front();
                que.pop();
                if(node->val==B->val){
                    if(is_true(node,B)) return true;
                }
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
            
        }
        return false;
    }
};

剑指 Offer 27. 二叉树的镜像

使用层次遍历法进行镜像，交叉左右节点

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* mirrorTree(TreeNode* root) {
        if(root==NULL) return NULL;
        queue<TreeNode*> que;
        que.push(root);
        while(!que.empty()){
            int size=que.size();
            for(int i=0;i<size;i++){
                TreeNode* node=que.front();
                que.pop();
                TreeNode* temp=node->left;
                node->left=node->right;
                node->right=temp;
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
        }
        return root;
    }
};

剑指 Offer 28. 对称的二叉树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool is_syem(TreeNode* left,TreeNode* right){
        //使用递归进行判断
        if(left==NULL&&right==NULL) return true;
        if(left==NULL) return false;//只有左边为空
        if(right==NULL) return false;
        if(left->val!=right->val) return false;

        //左右节点的值都是相等的
        bool label1=is_syem(left->left,right->right);
        bool label2=is_syem(left->right,right->left);

        return label1&&label2;

    }
    bool isSymmetric(TreeNode* root) {
        if(root==NULL) return true;
        return is_syem(root->left,root->right);
    }
};

剑指 Offer 30. 包含min函数的栈

class MinStack {
public:
    /** initialize your data structure here. */
    stack<int> st;
    map<int,int> m;//map会自动排序，key是插入的数，value是这个数的个数
    MinStack() {

    }
    
    void push(int x) {
        st.push(x);
        m[x]++;
    }
    
    void pop() {
        int val=st.top();
        m[val]--;
        st.pop();
    }
    
    int top() {
        return st.top();
    }
    
    int min() {
        int min_num=0;
        for(auto it=m.begin();it!=m.end();it++){
            if(it->second>0){//第一个就是最小值
                min_num=it->first;
                break;
            }
        }
        return min_num;
    }
};

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack* obj = new MinStack();
 * obj->push(x);
 * obj->pop();
 * int param_3 = obj->top();
 * int param_4 = obj->min();
 */

剑指 Offer 31. 栈的压入、弹出序列

根据给定的数组模拟栈的压入、弹出过程

class Solution {
public:
    bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
        stack<int> st;
        int j=0;
        for(int i=0;i<pushed.size();i++){
            st.push(pushed[i]);
            while(!st.empty()&&popped[j]==st.top()){//如果要弹出
                st.pop();
                j++;
            }
        }
        if(st.empty()) return true;//如果最后所有元素都弹出去了，说明弹出顺序是正确的
        return false;
    }
};

剑指 Offer 32 - I. 从上到下打印二叉树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> levelOrder(TreeNode* root) {
        //层次遍历法
        vector<int> result;
        if(root==NULL) return result;
        queue<TreeNode*> que;
        que.push(root);
        while(!que.empty()){
            
            int size=que.size();
            for(int i=0;i<size;i++){
                TreeNode* node=que.front();
                result.push_back(node->val);
                que.pop();
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
        }
        return result;
    }
};

剑指 Offer 32 - II. 从上到下打印二叉树 II

层次遍历法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> result;
        if(root==NULL) return result;
        queue<TreeNode*> que;
        que.push(root);
        while(!que.empty()){
            int size=que.size();
            vector<int> temp;
            for(int i=0;i<size;i++){
                TreeNode* node=que.front();
                que.pop();
                temp.push_back(node->val);
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
            result.push_back(temp);
        }
        return result;
    }
};

剑指 Offer 32 - III. 从上到下打印二叉树 III

注意这道题是整个一行的顺序反过来，而不是只对一个节点的左右节点交换顺序
错误写法：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> result;
        if(root==NULL) return result;
        bool label=false;//true:从左到右的顺序打印  false:从右到左的顺序
        queue<TreeNode*> que;
        que.push(root);
        while(!que.empty()){
            int size=que.size();
            vector<int> temp;
            for(int i=0;i<size;i++){
                TreeNode* node=que.front();
                que.pop();
                temp.push_back(node->val);
                if(!label){
                    if(node->right) que.push(node->right);
                    if(node->left) que.push(node->left);
                }
                else{
                    if(node->left) que.push(node->left);
                    if(node->right) que.push(node->right);
                }
            }
            label=~label;
            result.push_back(temp);

        }
        return result;
    }
};

正确写法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> result;
        if(root==NULL) return result;
        bool label=true;//true:从左到右的顺序打印  false:从右到左的顺序
        queue<TreeNode*> que;
        que.push(root);
        while(!que.empty()){
            int size=que.size();
            vector<int> temp;
            for(int i=0;i<size;i++){
                TreeNode* node=que.front();
                que.pop();
                temp.push_back(node->val);
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
                
            }
            if(label==false) reverse(temp.begin(),temp.end());
            label=!label;
            result.push_back(temp);

        }
        return result;
    }
};

剑指 Offer 33. 二叉搜索树的后序遍历序列

class Solution {
public:
    bool trans(vector<int>& postorder,int start,int end){
        //[start,end]
        if(end-start<=1) return true;
        int root=postorder[end];//根节点的值
        int i=start;
        for(;i<end;i++){
            if(postorder[i]>root) break;
        }
        //i为右子树的起始位置
        for(int j=i;j<end;j++){
            if(postorder[j]<root) return false;

        }
        bool left=trans(postorder,start,i-1);
        bool right=trans(postorder,i,end-1);
        return left&&right;

    }
    bool verifyPostorder(vector<int>& postorder) {
        //后序遍历：左右中
        if(postorder.size()==0) return true;
        return trans(postorder,0,postorder.size()-1);

    }
};

剑指 Offer 34. 二叉树中和为某一值的路径

采用递归进行寻找，由于节点值可能为负，所以在判断返回条件的时候不能说当前target<0就返回

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> result;
    void look_target(TreeNode* node,int target,vector<int> &path){
        if(node->left==NULL&&node->right==NULL&&target==0){
            result.push_back(path);
            return;
        }
        if(node->left){
            int val=node->left->val;
            path.push_back(val);
            look_target(node->left,target-val,path);
            path.pop_back();
        }
        if(node->right){
            int val=node->right->val;
            path.push_back(val);
            look_target(node->right,target-val,path);
            path.pop_back();
        }
    }
    vector<vector<int>> pathSum(TreeNode* root, int target) {
        if(root==NULL) return result;
        vector<int> path;
        path.push_back(root->val);
        look_target(root,target-root->val,path);
        return result;
        
    }
};

剑指 Offer 35. 复杂链表的复制

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* next;
    Node* random;
    
    Node(int _val) {
        val = _val;
        next = NULL;
        random = NULL;
    }
};
*/
class Solution {
public:
    Node* copyRandomList(Node* head) {
        if(head==NULL) return NULL;
        Node* new_head=new Node(head->val);//因为是复制，所以必须new一个新地址充当复制链表的头结点
        Node* temp=new_head;
        Node* virtual_head=new Node(0);//原链表的虚拟头结点
        virtual_head->next=head;
        //先处理next节点的指向
        while(head->next){
            Node* next=new Node(head->next->val);//因为是复制，所以必须new一个新地址
            temp->next=next;
            head=head->next;
            temp=temp->next;
        }
        //处理random节点的指向
        head=virtual_head->next;//原链表中的处理节点
        temp=new_head;//复制链表中的处理节点
        while(head){
            if(head->random==NULL){
                head=head->next;
                temp=temp->next;
                continue;
            }
            //注意这里不能判断val值是否相等，因为多个节点中的val值可能相等，所以会导致random指针指向错误
            int gap=0;//头节点距离random节点有多远
            Node* node_gap=virtual_head->next;//这里不是head，head只是处理过程的一个节点
            while(node_gap!=head->random){//找到地址相同的
                node_gap=node_gap->next;
                gap++;
            }
            
            Node* node=new_head;
            while(gap--) node=node->next;
            temp->random=node;
            head=head->next;
            temp=temp->next;
        }
        return new_head;
    }
};

剑指 Offer 36. 二叉搜索树与双向链表

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;

    Node() {}

    Node(int _val) {
        val = _val;
        left = NULL;
        right = NULL;
    }

    Node(int _val, Node* _left, Node* _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};
*/
class Solution {
public:
    vector<Node*> vec;//存放中序遍历结果
    void mid_look(Node* node){
        //中序遍历的结果就是按照节点值从小到大的顺序
        if(node==NULL){
            return;
        }
        
        mid_look(node->left); 
        vec.push_back(node);
        mid_look(node->right);
        
    }
    Node* treeToDoublyList(Node* root) {
        if(root==NULL) return NULL;
        mid_look(root);
        for(int i=0;i<vec.size()-1;i++){
            Node* node=vec[i];
            Node* next=vec[i+1];
            node->right=next;
            next->left=node;
        }
        vec[vec.size()-1]->right=vec[0];
        vec[0]->left=vec[vec.size()-1];

        return vec[0];
    }
};

剑指 Offer 38. 字符串的排列

去重可以参考下面的讲解：
全排列去重

class Solution {
public:
    vector<string> result;
    void permu(string s,string path,vector<int> &used_char){
        if(path.size()==s.size()){
            result.push_back(path);
            return;
        }
        for(int i=0;i<s.size();i++){
            if(i>0&&s[i]==s[i-1]&&used_char[i-1]==0) continue;//同树层相同元素去重
            if(used_char[i]==0){//代表还没用过
               used_char[i]=1; 
               path+=s[i];
               permu(s,path,used_char);
               path.pop_back();
               used_char[i]=0;
            }

        }
    }
    vector<string> permutation(string s) {
        string path="";
        sort(s.begin(),s.end());
        vector<int> used_char(s.size(),0);
        permu(s,path,used_char);
        return result;
    }
};

剑指 Offer 40. 最小的k个数

法一：直接使用api
sort函数的排序方法类似于快排方法，时间复杂度为n*log2(n)

class Solution {
public:
    vector<int> getLeastNumbers(vector<int>& arr, int k) {
        vector<int> result(k,0);
        sort(arr.begin(),arr.end());
        for(int i=0;i<k;i++){
            result[i]=arr[i];
        }
        return result;
    }
};

法二：使用快排

class Solution {
public:
        // 快速排序 不稳定排序  时间复杂度O（n*log n），空间复杂度O(logn)(递归会使用栈）
        //1、选取第一个数为基准
        //2、将比基准小的数交换到前面，比基准大的数交换到后面
        //3、对左右区间重复第二步，直到各区间只有一个数
    void quickSort(vector<int>& vec,int index_start,int index_end){
        //使用递归 传入整个数组和需要处理的数据起始位置[index_start，index_end]
        if(index_end-index_start<=0) return;//区间内只有一个数
        int index=index_start;
        for(int i=index_start+1;i<=index_end;i++){
            if(vec[i]<vec[index]){
                //把vec[i]的值换到index前面去
                for(int j=i;j>index;j--){
                    swap(vec[j],vec[j-1]);
                }
                
                index++;//更新基准的位置
            }
        }
        quickSort(vec,index_start,index-1);
        quickSort(vec,index+1,index_end);
    }
    vector<int> getLeastNumbers(vector<int>& arr, int k) {
        vector<int> result(k,0);
        quickSort(arr,0,arr.size()-1);
        for(int i=0;i<k;i++){
            result[i]=arr[i];
        }
        return result;
    }
};

剑指 Offer 42. 连续子数组的最大和

使用前缀和的思想

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int max=nums[0];
        int result=0;
        for(int i=0;i<nums.size();i++){
            result+=nums[i];
            if(result>max){              
                max=result;               
            }
            if(result<0){
                result=0;
            }
        }
        return max;
    }
};

剑指 Offer 45. 把数组排成最小的数

class Solution {
public:
    bool static cmp(int a,int b){
        //按照a和b转换成string字符串结合起来的最小结果来决定a和b的前后位置
        string s1=to_string(a);
        string s2=to_string(b);
        return (s1+s2)<(s2+s1);
    }
    string minNumber(vector<int>& nums) {
        sort(nums.begin(),nums.end(),cmp);
        string result;
        for(auto num:nums){
            result+=to_string(num);
        }
        
        return result;
    }
};

剑指 Offer 46. 把数字翻译成字符串

使用动态规划
感觉这道题也可以用回溯里面的分割来做，每一层的节点值代表本次分割的情况，比如1223，第一层可以是1或者12

class Solution {
public:
    int translateNum(int num) {
        string str=to_string(num);
        int size=str.size();
        if(size<=1) return size;
        vector<int> dp(size+1,0);//dp[i]表示i个数字有多少种翻译方法
        dp[0]=1;
        dp[1]=1;
        for(int i=2;i<=size;i++){
            string s="";
            s+=str[i-2];
            s+=str[i-1];
  
            int k=stoi(s);
            if(k>=10&&k<=25){//两个条件都必须有，因为可能是06之类的
                dp[i]=dp[i-1]+dp[i-2];
            }
            else{
                dp[i]=dp[i-1];//第i位的数字和i-1位数字的分割方法进行组合
            }
        }
        return dp[size];
    }
};

剑指 Offer 47. 礼物的最大价值

class Solution {
public:
    int maxValue(vector<vector<int>>& grid) {
        int m=grid.size();
        int n=grid[0].size();
        vector<vector<int>> dp(m,vector<int>(n,0));//[i,j]位置的最大值
        for(int i=0;i<n;i++){
            if(i==0) dp[0][0]=grid[0][0];
            else{
                dp[0][i]=dp[0][i-1]+grid[0][i];
            }
        }
        for(int i=1;i<m;i++){
            dp[i][0]=dp[i-1][0]+grid[i][0];
        }
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                dp[i][j]=max(dp[i-1][j]+grid[i][j],dp[i][j-1]+grid[i][j]);
            }
        }
        return dp[m-1][n-1];
    }
};

剑指 Offer 48. 最长不含重复字符的子字符串

使用动态规划+哈希表完成

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        if(s.size()<=1) return s.size();
        unordered_map<char,int> m;//key记录最长子字符串的字符，value记录对应的字符在s中的下标位置
        vector<int> dp(s.size(),1);//dp[i]:字符串的最长子字符串以第i个字符结尾的
        m.insert(pair<char,int>(s[0],0));
        int start=0;//最长子字符串的长度的开始位置
        int max=0;//最长子字符串的长度
        for(int i=1;i<dp.size();i++){
            auto it=m.find(s[i]);
            if(it==m.end()){
                //说明不重复
                m.insert(pair<char,int>(s[i],i));
                dp[i]=dp[i-1]+1;
               
            }
            else{
                int index=it->second;//重复的下标位置
                for(int j=start;j<=index;j++){
                    m.erase(s[j]);//删掉哈希表重复位置之前的所有元素
                }
                m.insert(pair<char,int>(s[i],i));
                dp[i]=i-index;//从index后一位算起
                start=index+1;//更新开始位置
            }
            if(dp[i]>max) max=dp[i];
        }
        return max;

    }
};

剑指 Offer 49. 丑数

使用动态规划和三指针
这里需要注意下去重的问题，如果某次寻找丑数，找到了下一个丑数10，则pointer2和pointer5都需要加一，因为5乘2等于10， 5乘2也等于10，这样可以确保10只被数一次。

代码里面是用的三个并行的if操作，所以包含去重操作了

class Solution {
public:
    int nthUglyNumber(int n) {
        //丑数*质因子可以得到丑数
        vector<int> dp(n+1,1);
        int p1=1,p2=1,p3=1;//三个指针分别代表*2、*3、*5操作，如果某个操作被用过了，那么就将该指针+1
        for(int i=2;i<dp.size();i++){
            int val=min(min(2*dp[p1],3*dp[p2]),5*dp[p3]);
            if(val==2*dp[p1]) p1++;
            if(val==3*dp[p2]) p2++;
            if(val==5*dp[p3]) p3++;
            dp[i]=val;

        }
        return dp[n];
    }
};

剑指 Offer 50. 第一个只出现一次的字符

class Solution {
public:
    char firstUniqChar(string s) {
        if(s.size()==0) return ' ';
        unordered_map<char,int> m;
        
        for(int i=0;i<s.size();i++){
            m[s[i]]++;
        }
        for(int i=0;i<s.size();i++){
            if(m[s[i]]==1){
                return s[i];
            }
        }
        return ' ';
    }
};

剑指 Offer 52. 两个链表的第一个公共节点

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode* node1=headA;
        ListNode* node2=headB;
        int size_A=0;
        int size_B=0;
        //算出两个链表的长度
        while(node1){
            size_A++;
            node1=node1->next;
        }
        while(node2){
            size_B++;
            node2=node2->next;
        }
        //对两个链表进行尾对齐
        int path=abs(size_A-size_B);
        node1=headA;
        node2=headB;
        if(size_A>size_B){
            
            while(path--){
                node1=node1->next;
            }
            while(node1&&node2){
                if(node1==node2) return node1;
                node1=node1->next;
                node2=node2->next;
            }
        }
        else{
            while(path--){
                node2=node2->next;
            }
            while(node1&&node2){
                if(node1==node2) return node1;
                node1=node1->next;
                node2=node2->next;
            }                
            
        }

        return NULL;//没找到返回NULL
    }
};

剑指 Offer 53 - I. 在排序数组中查找数字 I

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int result=0;
        for(int i=0;i<nums.size();i++){
            if(nums[i]==target){
                result++;
            }
        }
        return result;
    }
};

剑指 Offer 53 - II. 0～n-1中缺失的数字

class Solution {
public:
    int missingNumber(vector<int>& nums) {
        int result=0;
        vector<int> vec(nums.size()+1,0);
        for(int i=0;i<nums.size();i++){
            vec[nums[i]]=1;
        }
        for(int i=0;i<vec.size();i++){
            if(vec[i]==0){
               result=i; 
               break;
            }
        }
        return result;
    }
};

剑指 Offer 54. 二叉搜索树的第k大节点

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;

    Node() {}

    Node(int _val) {
        val = _val;
        left = NULL;
        right = NULL;
    }

    Node(int _val, Node* _left, Node* _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};
*/
class Solution {
public:
    vector<Node*> vec;//存放中序遍历结果
    void mid_look(Node* node){
        //中序遍历的结果就是按照节点值从小到大的顺序
        if(node==NULL){
            return;
        }
        
        mid_look(node->left); 
        vec.push_back(node);
        mid_look(node->right);
        
    }
    Node* treeToDoublyList(Node* root) {
        if(root==NULL) return NULL;
        mid_look(root);
        for(int i=0;i<vec.size()-1;i++){
            Node* node=vec[i];
            Node* next=vec[i+1];
            node->right=next;
            next->left=node;
        }
        vec[vec.size()-1]->right=vec[0];
        vec[0]->left=vec[vec.size()-1];

        return vec[0];
    }
};

剑指 Offer 55 - I. 二叉树的深度

使用递归遍历搜所有达到根节点的路径的深度，再选出最大深度

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int result=0;
    void max_depth(TreeNode* root,int depth){
        if(root==NULL){
            if(depth>result) result=depth;
            return;
        }
        max_depth(root->left,depth+1);
        max_depth(root->right,depth+1);

    }
    int maxDepth(TreeNode* root) {
        max_depth(root,0);
        return result;
    }
};

剑指 Offer 55 - II. 平衡二叉树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int max_depth=0;
    void is_banlanced(TreeNode* root,int depth){
        //递归遍历计算树的深度
        if(root==NULL){
            if(max_depth<depth) max_depth=depth;
            return;
        }
        is_banlanced(root->left,depth+1);
        is_banlanced(root->right,depth+1);


    }

    bool isBalanced(TreeNode* root) {
        if(root==NULL) return true;
        bool label1=true;//左子树是否为平衡二叉树的标志位
        bool label2=true;//右子树是否为平衡二叉树的标志位
        if(root->left) label1=isBalanced(root->left);
        if(root->right) label2=isBalanced(root->right);
        
        max_depth=0;
        is_banlanced(root->right,0);
        int depth_right=max_depth;//右子树的深度

        max_depth=0;
        is_banlanced(root->left,0);
        int depth_left=max_depth;//左子树的深度

        //若当前节点左右子树的深度相差超过1
        if(abs(depth_left-depth_right)>1) return false;

        //只有当前节点、当前节点的左右子树都符合要求时才会返回true
        return label1&&label2;
    }
};

剑指 Offer 57. 和为s的两个数字

法一：暴力解法+判断。超时
两层for循环 O（n^2)

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
   
        vector<int> result;
        if(nums.size()<=1) return result;

        for(int i=0;i<nums.size();i++){
            if(nums[i]>target) break;
            for(int j=i+1;j<nums.size();j++){
                if(nums[i]+nums[j]>target) break;
                if(nums[i]+nums[j]==target){
                    result.push_back(nums[i]);
                    result.push_back(nums[j]);
                    return result;
                }
            }
        }
        return result;
    }
};

法二：
时间复杂度O（n)

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        vector<int> result;
        if(nums.size()<=1) return result;
        int i=0,j=nums.size()-1;//使用双指针从头尾开始逼近
        
        for(;i>=0&&j<nums.size()&&i<j;){
            int sum=nums[i]+nums[j];
            if(sum>target){
                j--;
                continue;
            }
            else if(sum<target){
                i++;
                continue;
            }
            else{
                result.push_back(nums[i]);
                result.push_back(nums[j]);
                break;
            }
        }
        return result;
    }
};

剑指 Offer 58 - I. 翻转单词顺序

这道题虽然是简单题，但是需要注意考虑全是空格的情况

class Solution {
public:
    string reverseWords(string s) {
        // if(s.size()==0) return s;//记得判断特殊情况
        string result="";
        vector<string> vec;
        reverse(s.begin(),s.end());
        //“去掉”前后空格
        int i=0;
        for(;i<s.size();i++){
            if(s[i]!=' '){
                break;
            }
        }
        if(i==s.size()) return "";//去除全是空格的情况
        int j=s.size()-1;
        while(s[j]==' '){
            j--;
        }

        string str="";
        for(int k=i;k<=j;){
            if(s[k]!=' '){
                str.push_back(s[k]);
                k++;
            }
            else{//遇到空格就放入单词
                reverse(str.begin(),str.end());
                vec.push_back(str);
                while(s[k]==' ') k++;
                str="";
            }
        }
        reverse(str.begin(),str.end());
        vec.push_back(str);
        for(int i=0;i<vec.size();i++){
            result+=vec[i];
            if(i!=vec.size()-1) result+=" ";
        }
        return result;
    }
};

剑指 Offer 59 - II. 队列的最大值

class MaxQueue {
public:
    queue<int> que;
    map<int,int,greater<int>> m;//按照key的值从大到小排序
    MaxQueue() {

    }
    
    int max_value() {
        if(que.size()==0) return -1;
        auto it=m.begin();
        int max_num=0;
        for(;it!=m.end();it++){
            if(it->second>0){
                max_num=it->first;
                break;
            }
        }
        return max_num;
    }
    
    void push_back(int value) {
        que.push(value);
        m[value]++;
    }
    
    int pop_front() {
        if(que.size()==0) return -1;
        m[que.front()]--;
        int val=que.front();
        que.pop();
        return val;
    }
};

/**
 * Your MaxQueue object will be instantiated and called as such:
 * MaxQueue* obj = new MaxQueue();
 * int param_1 = obj->max_value();
 * obj->push_back(value);
 * int param_3 = obj->pop_front();
 */

剑指 Offer 60. n个骰子的点数

剑指 Offer 61. 扑克牌中的顺子

class Solution {
public:
    bool isStraight(vector<int>& nums) {
        //0相当于是癞子
        int num_zero=0;
        sort(nums.begin(),nums.end());
        int i=0;
        for(;i<nums.size();i++){
            if(nums[i]==0) num_zero++;
            else{
                break;
            }
        }
        int gap=0;
        for(;i<nums.size()-1;i++){
            if(nums[i]==nums[i+1]) return false;
            if(nums[i+1]-nums[i]>1) gap+=(nums[i+1]-nums[i]-1);//其他数之间的空隙
        }
        if(num_zero>=gap) return true;
        return false;
    }
};

剑指 Offer 63. 股票的最大利润

如果一旦出现加上某天相比前一天卖出的利润小于0，那么就重新开始计算

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int result=0;
        int max=0;
        for(int i=1;i<prices.size();i++){
            result+=prices[i]-prices[i-1];
            if(result<0){
                result=0;
                
            }
            else{
                if(result>max) max=result;
            }
        }
        return max;
    }
};

剑指 Offer 64. 求1+2+…+n

这道题其实就是在提示用递归的方法做

class Solution {
public:
    int sum=0;
    void sum_num(int n){
        if(n==0) return;
        sum+=n;
        sum_num(n-1);
        
    }
    int sumNums(int n) {
        sum_num(n);
        return sum;
    }
};

剑指 Offer 67. 把字符串转换成整数

class Solution {
public:
    int strToInt(string str) {
        //分情况进行讨论
        int result=0;
        int i=0;
        for(;i<str.size();i++){
            if(str[i]!=' '){
                break;
            }
        }
        if(i==str.size()) return 0;//字符串为空
        int j=i;
        long int num=0;
        if(str[i]=='-'){
            int a=0;
            for(j=i+1;j<str.size();j++){
                if(isdigit(str[j])){

                    num=num*10+str[j]-'0';
                    if(-num<INT_MIN) return INT_MIN;
                }
                else break;
            }
            num=-num;
            if(num<INT_MIN){
                result=INT_MIN;
            }
            else result=num;
        }
        if(str[i]=='+'){
            int a=0;
            for(j=i+1;j<str.size();j++){
                if(str[j]>='0'&&str[j]<='9'){
                    a=str[j]-'0';
                    num=num*10+a;  
                    if(num>INT_MAX) return INT_MAX;                  
                }
                else break;
            }
          
           result=num;
        }
        if('0'<=str[i]<='9'){
        // if(str[i]<='9'&&str[i]>='0'){
            int a=0;
            for(j=i;j<str.size();j++){
                if(str[j]>='0'&&str[j]<='9'){
                    a=str[j]-'0';
                    num=num*10+a;   
                    if(num>INT_MAX) return INT_MAX;                  
                }
                else break;
            }
            result=num;
        }
        return result;

    }
};

剑指 Offer 68 - I. 二叉搜索树的最近公共祖先

利用好二叉搜索树的特性，先判断当前节点是否符合要求，再根据节点值一步步地向下进行搜索

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
       if(root==q||root==p||root==NULL||(root->val<p->val&&root->val>q->val)||(root->val>p->val&&root->val<q->val)){
           return root;
       }
       TreeNode* node;
       if(root->val<q->val&&root->val<p->val) node=lowestCommonAncestor(root->right,p,q);
       if(root->val>q->val&&root->val>p->val) node=lowestCommonAncestor(root->left,p,q);
       return node;
        
    }
};

剑指 Offer 68 - II. 二叉树的最近公共祖先

使用递归遍历，使用前序遍历进行搜寻，如果left和right只有一个为空，说明这两个节点再同一边，其中一个节点为公共祖先；如果两个都为空，说明没找到；如果两个都不为空，说明此时的节点就是最近公共祖先

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==p||root==q||root==NULL){
            return root;
        }

        TreeNode* left=lowestCommonAncestor(root->left,p,q);
        TreeNode* right=lowestCommonAncestor(root->right,p,q);

        if(left==NULL&&right==NULL) return NULL;
        else if(left==NULL) return right;
        else if(right==NULL) return left;
        else return root;
       

    }
};