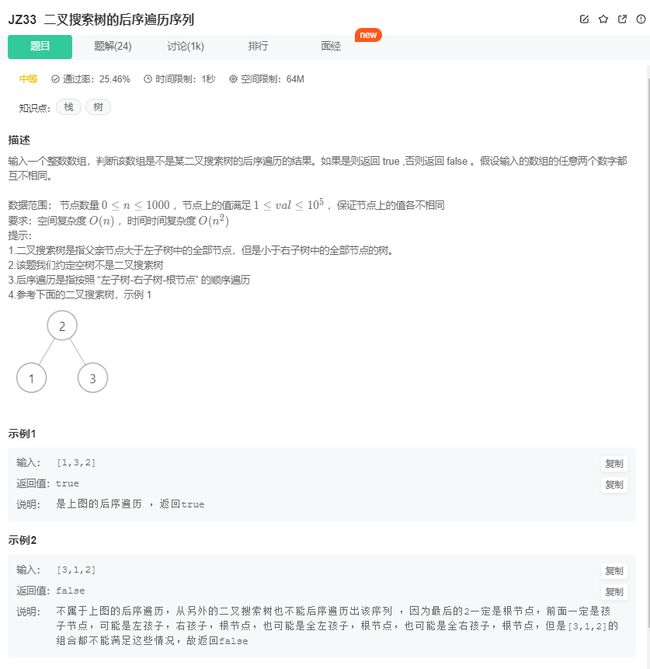
二叉搜索树的后序遍历序列验证
二叉搜索树的后续遍历序列验证
这道题有点抽象,主要是如果没有对二叉搜索树的遍历验证有了解会比较难想象,我也在这里卡了很久。
本质就是找到根节点,判断右子树的所有节点(根节点和所有子节点)都大于根节点,左子树都小于。
原题
二叉搜索树概念
二叉搜索树,又称二叉排序树,若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉搜索树
二叉搜索树的特性:
如下图,就是一颗二叉搜索树,有如下性质:
-
任意节点的左子树的所有子节点(非空)的数值都小于它的根节点,同理右子树的所有节点的数值(非空)都大于根节点。
-
任意节点的左右子树也是二叉搜索树
-
有序性,中序遍历的结果是升序的
下图的二叉查找树的中序遍历(左根右)为:[1,2,3,4,5,6,7,8,9,10], 可以看出是从小到大有序的
题目解法(java实现)
1. 递归
因为题目给的是后序遍历后的数组,同时我们知道了二叉搜索树的性质,可以知道这个数组是部分乱序的,后续遍历的顺序是左右根,所有二叉搜索树的根节点在数组的最后一个,我们先从这个入手,想要判断这个二叉搜索树是否合法,我们就要判断根节点的左子树的全部节点的值是否都小于根节点的值,右子树的全部节点的值是否都大于根节点;因此,我们先用一个for循环,找到左子树和右子树在数组里的分界线
如上图的例子后序遍历数组是:[1,3,2,5,6,4,8,10,9,7],左右子树分割为[ 1,3,2,5,6,4 | 8,10,9 | 7 ] ,可以发现左子树都比最后一个数组节点小,直到找到比根节点大的值,就能确定左右子树在数组的边界
然后再遍历右子树,判断是否都大于根节点,如果出现小于根节点的可以直接判定,这棵树不是二叉搜索树
/**
* @param: seq 后序遍历的数组
* @param: l-r 判断这颗树或子树在数组里面的范围
**/
private boolean isValid(int[] seq, int l, int r){
int root = seq[r]; // 根节点
int i; // 记录左右子树在数组的边界下标
// 找出左子树和右子树的边界下标
for(i = l; i < r; i++) {
if(seq[i] > root)
break;
}
// 直接判断右子树是否符合条件(都大于根节点)
for(int j = i; j < r; j++) {
if(seq[j] < root)
return false;
}
}
理解了上面的代码后,就可以上手递归了,不就是多次重复上面的操作,不断分割左右子树,传入不同的下标范围嘛
剩下一个问题就是递归的终止条件是啥?当我们传 isValid(int[] seq, int l, int r) 我们通过 i 来分割左右子树
return isValid(seq, l, i-1) && isValid(seq, i, r-1);
那么当分割到只剩下一个节点的时候,即 l = i-1或 i = r-1 时,下次递归我们得到结果就 l <= r ,并且中途没有检测出和二叉搜索树矛盾的地方(即右子树出现大于根节点的情况return false),我们就直接返回true,完整代码如下
public class Solution {
public boolean VerifySquenceOfBST(int [] sequence) {
if(sequence.length == 0) {
return false;
}
return isValid(sequence, 0, sequence.length-1);
}
private boolean isValid(int[] seq, int l, int r){
if(l >= r) // 递归出口
return true;
int root = seq[r];
int i;
// 找出左子树和右子树的边界下标
for(i = l; i < r; i++) {
if(seq[i] > root)
break;
}
// 直接判断右子树是否符合条件(都大于根节点)
for(int j = i; j < r; j++) {
if(seq[j] < root)
return false;
}
// 也可以倒过来,先遍历右子树,再根据左子树判断
return isValid(seq, l, i-1) && isValid(seq, i, r-1);
}
}
算法时间复杂度:O(n2) 空间复杂度:O(n)
2. 单调栈
单调栈会比递归更难理解一些,但是原理是有相似的,只不过使用了栈来辅助
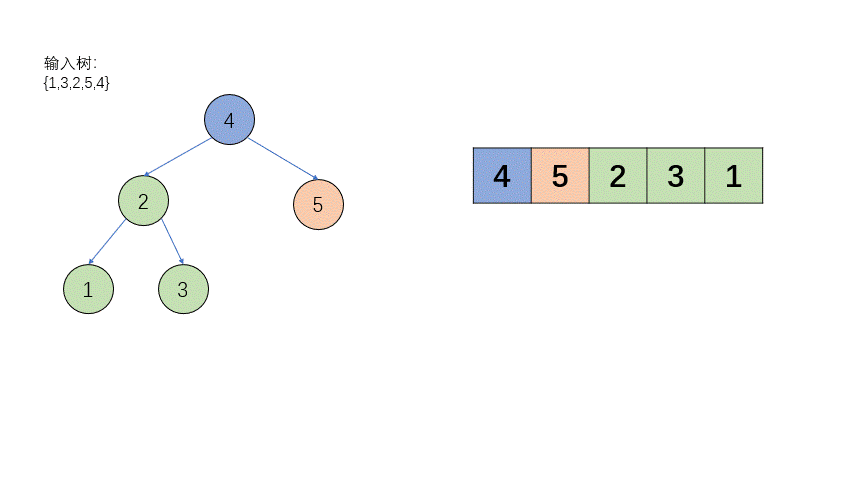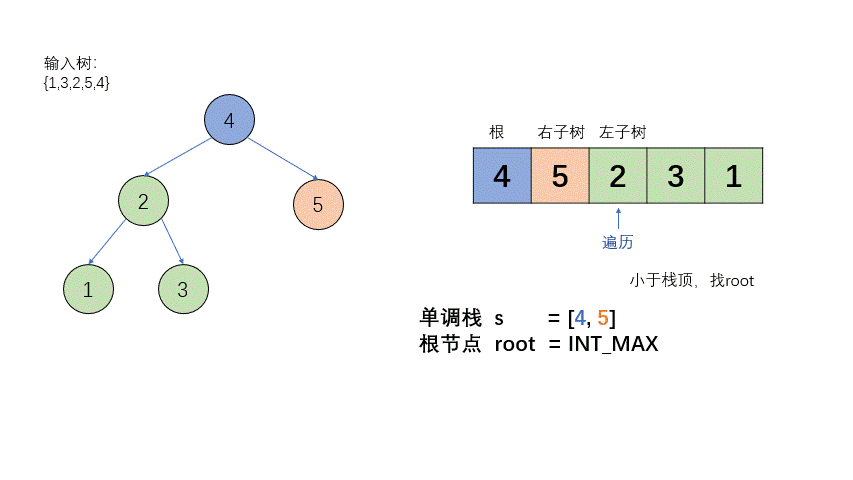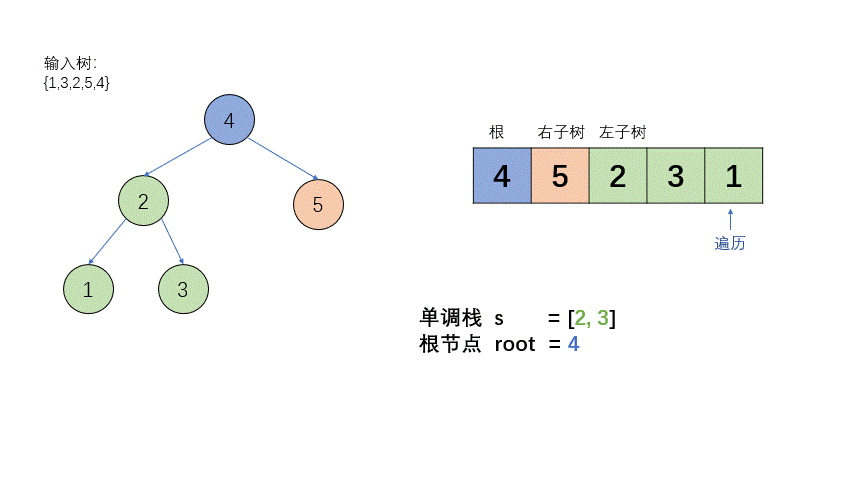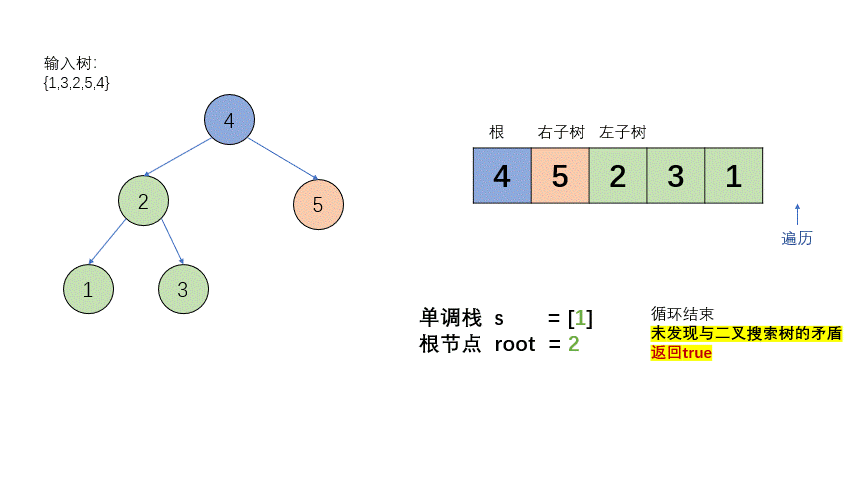
过程如上:乍一看肯定很懵,我们细细分析这个过程:
- 数组逆序遍历(即后序遍历的相反顺序:根右左),由于是单点栈,所以一旦出现逆序(即本来是从栈底到栈顶是升序,出现一个比栈顶小的数),就弹出栈的所有比要加入栈的节点的值大的节点,从而保证单调性,我们发现这个时候,如果这棵树是二叉搜索树的话,弹出的最后一个比要入栈的节点大的元素,就是这颗树或子树的根节点,将其记录
- 因为一旦出现逆序的现象,就说明后面的数都是当前这个根节点的左子树(右子树已经确定,因为前面大于根节点的值被判定为右子树),而二叉搜索树的左子树是小于根节点的,因此,判断不是二叉搜索树的条件就是,一旦根节点 小于 下面要遍历的左子树的节点,我们就
return false;
具体代码如下:
public class Solution {
public boolean VerifySquenceOfBST(int [] sequence) {
if(sequence.length == 0)
return false;
Stack<Integer> stack = new Stack<>();
int root = Integer.MAX_VALUE; // 保证第一次没有根节点的情况下,不会直接返回false
for(int i = sequence.length-1; i >= 0; i--) {
// 如果左子树中的节点出现大于根节点的,不符合要求,直接返回false
if(sequence[i] > root)
return false;
// 找到左子树的开始节点,pop弹出右子树,记录最后一个节点为根节点,方便后面判断左子树中的节点是否都小于根节点
while(!stack.isEmpty() && stack.peek() > sequence[i]) {
root = stack.pop();
}
stack.add(sequence[i]);
}
return true;
}
}
算法时间复杂度:O(n) 空间复杂度:O(n)
希望以上能帮助到你理解这道题