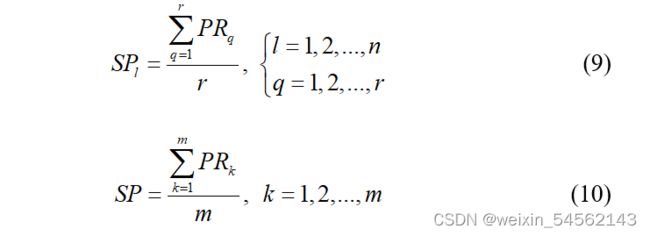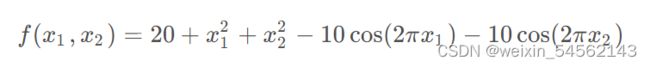多种智能优化算法性能对比(FHO,CO,SSA,PSO等)
1.方法介绍
1.1.火鹰优化算法(FHO)
FHO算法模拟了火鹰的觅食行为,是一个考虑放火、火势蔓延与捕捉猎物的过程,其算法流程如下图所示。
FHO数学模型描述如下:
Step 1: 首先,确定若干候选解X作为火鹰与猎物的位置向量,利用随机优化确定初始位置。表示如下:
 其中,N为候选解的总数,
其中,N为候选解的总数,![]() 表示第i个候选解的第j个决策变量,
表示第i个候选解的第j个决策变量,![]() 表示候选解的初始位置,
表示候选解的初始位置,![]() 表示第i个候选解的第j个决策变量候选解的最小最大边界,rand∈(0,1)。
表示第i个候选解的第j个决策变量候选解的最小最大边界,rand∈(0,1)。
Step 2: 其次,确定猎物与火鹰在搜索空间的位置,将候选解中的具有较好函数值的表示为火鹰的位置,其余的表示为猎物的位置;表示如下:
其中,![]() 表示搜索空间内m个猎物总数的第k个猎物,
表示搜索空间内m个猎物总数的第k个猎物,![]() 表示搜索空间内n个火鹰总数的第k个火鹰。
表示搜索空间内n个火鹰总数的第k个火鹰。
Step 3: 计算出火鹰与猎物之间的总距离;表示如下:
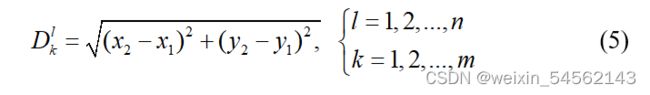 其中,
其中,![]() 表示第l只火鹰与第k只猎物之间的距离;
表示第l只火鹰与第k只猎物之间的距离;![]() 表示火鹰与猎物之间的距离。
表示火鹰与猎物之间的距离。
Step 4: 根据火鹰的两种不同的点火行为,进行位置更新,表示如下: 
![]() 表示第l只火鹰更新后的新位置,GB为全局最优解,表示主火;
表示第l只火鹰更新后的新位置,GB为全局最优解,表示主火;![]() 是搜索空间中的另一只火鹰,r1,r2∈(0,1)。
是搜索空间中的另一只火鹰,r1,r2∈(0,1)。
Step 5: 根据火鹰在领地内的移动行为进行位置的更新,表示如下:
 其中,
其中,![]() 表示第q只猎物更新后的新位置,
表示第q只猎物更新后的新位置,![]() 表示第l只火鹰属下的一个安全地点,r3,r4∈(0,1)。
表示第l只火鹰属下的一个安全地点,r3,r4∈(0,1)。
Step 6: 根据猎物的躲避行为,更新火鹰的位置, 表示如下:
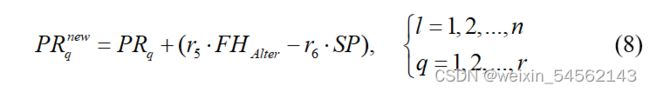 其中,
其中,![]() 表示搜索空间中的另一只火鹰,
表示搜索空间中的另一只火鹰,![]() 表示领地之外的安全地带,r5,r6∈(0,1)。
表示领地之外的安全地带,r5,r6∈(0,1)。
Step 7:以猎物聚集多的地方作为安全地带的选取,表示如下:
其中,![]() 表示被第l只火鹰包围的第q个猎物。
表示被第l只火鹰包围的第q个猎物。
1.2.猎豹优化算法(CO)
算法步骤如下:
Step1:根据猎豹在每个排列中的当前位置于任意步长更新每个排列中的位置,建议搜索策略;
Step2:为应对猎物直接暴露在猎豹视野的情况,建立坐等策略;
Step3:根据猎豹的速度于灵活度来制定攻击策略;
Step4:最后,算法不断根据不同状况更新相应的策略。
伪代码如下:
1.3.麻雀搜索算法(SSA)
Step1:对数据进行初始化
Step2:计算出适应度值,并进行排序;
Step3:不断更新发现者位置、加入者位置、防御者的位置,并计算出当前最佳适应度值并更新麻雀的位置。
Step4:通过判断是否满足条件,满足则退出,输出结果,否则,继续迭代。
具体模型参考【】;
算法流程图如下:
1.4.粒子群优化算法(PSO)
粒子群优化算法(PSO)是由Eberhart和Kennedy于1995年提出的,根据鸟群觅食行为所开发的一种仿生算法。
Step1:初始化粒子群,包括群体规模N,每个粒子的位置和速度。
Step2:计算粒子适应度。
Step3:比较并找出个体与全体最优值。
Step4:迭代更新粒子位置和速度。
Step5:判断算法终止条件是否满足:若是,则结束算法并输出优化结果;否则返回(2)
具体模型参考【】;
算法流程如下:
2.测试结果分析
2.1.选取测试函数
函数一:Griewank函数(检测算法跳出局部的能力)
函数二:Rosenbrock函数(检测算法寻得全局最优的能力)
函数三:Ackley函数(检测算法的全局收敛速度)
函数四:Rastrign函数(检测在解有规律的一种情况,算法的实用性)
2.2.结果呈现
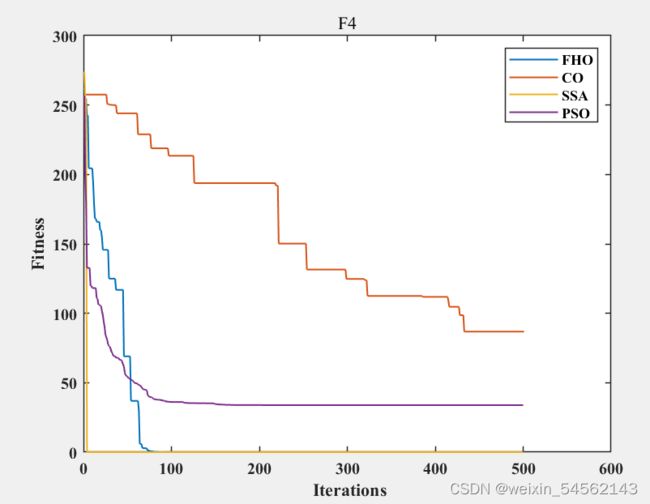
所有的算法测试时都选取了30个个体,迭代次数为500次。算法比较的结果如下:
2.2.1.迭代曲线
函数一:
其他参数对比(表中数据对应关系为:CO,FHO,PSO,SSA):
其他参数对比:
其他参数对比:
其他参数对比:
3.结论
尽管FHO与CO算法是这两年提出的新算法,但不见得要比先前提出的一些算法的效果要好。可以看出,这些算法中,SSA算法的收敛效果最好,且不会陷入局部最优。而并非一些新的算法有更好的性能,只是可能大概也许没有人对这些算法进行一个对比而已。(仅个人拙见,应该是还有很多不足之处,因为本人也是刚刚学习一些东西。这些其实是本人之前有学习和了解的一些智能算法,现在刚好在这个平台上记录一下自己的学习过程。还有许多算法未完全进行描述,等以后再补充,嘿嘿。)
参考文献
[1] Fire Hawk Optimizer: a novel metaheuristic algorithm | SpringerLink
[2] https://www.nature.com/articles/s41598-022-14338-z
[3] https://doi.org/10.1080/21642583.2019.1708830
[4] Kennedy, J., & Eberhart, R. (1995, November). Particle swarm optimization. In Proceedings of ICNN'95-international conference on neural networks (Vol. 4, pp. 1942-1948). IEEE.