Leetcode.689 三个无重叠子数组的最大和(滑动窗口)
难度:困难
给你一个整数数组 nums 和一个整数 k ,找出三个长度为 k 、互不重叠、且 3 * k 项的和最大的子数组,并返回这三个子数组。
以下标的数组形式返回结果,数组中的每一项分别指示每个子数组的起始位置(下标从 0 开始)。如果有多个结果,返回字典序最小的一个。
示例1:
输入:nums = [1,2,1,2,6,7,5,1], k = 2
输出:[0,3,5]
解释:子数组 [1, 2], [2, 6], [7, 5] 对应的起始下标为 [0, 3, 5]。
也可以取 [2, 1], 但是结果 [1, 3, 5] 在字典序上更大。
示例2:
输入:nums = [1,2,1,2,1,2,1,2,1], k = 2
输出:[0,2,4]
提示:
· 1 <= nums.length <= 2 * 104
· 1 <= nums[i] < 216
· 1 <= k <= floor(nums.length / 3)
举个例子,假设nums = {1, 2, 3, 1, 2, 4, 3, 2, 2, 4, 3, 1, 2},子序列长度k = 3。使用三个滑动窗口,每个窗口的长度为k = 3,每个窗口都用来框出一个子序列,要保证三个窗口不重叠。
定义sum1、sum2、sum3为三个串口内的元素之和,idx1、idx2、idx3为三个窗口的最后一个元素的位置(至于为什么是最后一个不是第一个,我在后面会解释)。下图示意一下三个窗口的含义。

题目中要求我们找到三个子序列元素之和最大的位置,我们用max_sum123表示最大值。这时我们需要思考两个主要问题:
- 一个窗口左右滑动时,我们如何快速求取这个窗口内的所有元素和sum?
- 如何通过滑动这三个窗口找到max_sum123?
下面逐个解决这两个问题。
1. 如何求窗口内的所有元素之和
如下图所示,窗口位于一个位置,我们计算得到它的元素之和sum。

我们将窗口向右滑动一下,计算新的sum值。我们并不需要将窗口内所有的元素累加起来,这样会做很多重复计算。我们只需要在前一次sum的基础上,减去左边离开窗口的元素的值,再加上右边新加入窗口的元素的值。这样,窗口的前后两个位置都包含的元素之和,就不需要再重复计算了。
注意,由于本例中由于k=3,将窗口内元素直接求和是做两次加减操作,向上文这样一减一加也是做两次加减操作。但如果k取一个较大的值,则求和要做k-1次加减,但一减一加依旧是两次加减,计算成本被大大降低。
然后我们探讨一下,窗口从最左端一直滑动到最右端的过程中,能使窗口内元素之和最大的窗口位置。用idx表示窗口的位置,则代码如下。
int sum = 0;
int max_sum = 0;
int max_idx;
for (int idx = 0; idx < nums.size(); idx++) {
sum += nums[idx];
if (idx >= k - 1) {
if (sum > max_sum) {
max_sum = sum;
max_idx = idx - k + 1;
}
sum -= nums[idx - k + 1];
}
}
2. 如何滑动窗口找到max_sum123
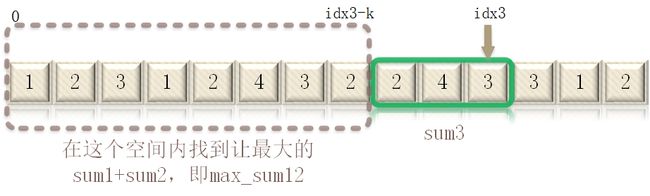
分解这个问题,我们先固定窗口3的位置,则sum3的值就是固定的了。如果我们想得到max_sum123,就要在序列3前面的空间内,找到sum1 + sum2的最大值,我们用max_sum12表示。因此,则有max_sum123 = max_sum12 + sum3。
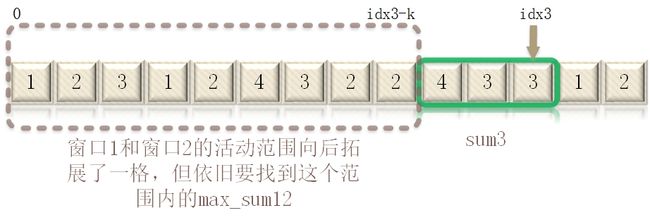
当然idx3不可能是固定的,让窗口3向后滑动一格,则窗口1和窗口2的可移动范围也变大了,但如果依旧想让max_sum123得到最大值,依旧是要找到窗口1和窗口2在活动范围内能得到的最大的max_sum12,并与当前的sum3相加。将计算结果与滑动前的max_sum123比较,如果更大则替换掉原先的max_sum123。
现在我们的问题被分解成了max_sum12。和之前一样,我们先固定窗口2的位置,则sum2的值就固定了,那么只有当窗口1的sum1在它的活动范围内取到最大值(记为max_sum1)时,两个窗口的元素和才能取到最大,即max_sum12 = max_sum1 + sum2。
窗口2向后滑动了也是同样的道理,这里就不再赘述了。
上面说了这么多,其实重点只是推导出下面这两个公式:
KaTeX parse error: No such environment: equation at position 7: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲max\_sum_{123}=…
3. 代码实现
最重要的两个问题解决了,下面继续分析题目。
首先确定三个窗口的初始状态。三个窗口都完全进入数组后的第一个状态是都位于最左端。计算三个窗口内的sum1、sum2、sum3,并于max_sum1、max_sum2、max_sum3进行比较。
第三个窗口向右滑动一格,则第二个窗口的活动范围就增大一格。让第二个窗口也向右滑动一格,则第一个窗口的活动范围也增大一格。第一个窗口向右滑动,计算此时的sum1,与max_sum1进行比较并更新max_sum1的值,并记录窗口的位置max_idx1。
根据前面推导出的关系式,继续计算max_sum12。比较max_sum1 + sum2与max_sum2的大小,如果max_sum1 + sum2大于max_sum2则替换max_sum2的值,并记录此时两个窗口的位置max_idx12_1和max_idx12_2。如果不大于,max_idx12_1和max_idx12_2的值均不改变。
注意,让前两个窗口内的元素之和最大的两窗口的位置,应该是max_idx_12和max_idx12_2——第一个窗口的位置是max_idx12_1而不能用max_idx1,这是因为在不满足max_sum1 + sum2大于max_sum2的情况下,有可能max_idx1记录的是已经向后滑动的位置,而max_idx12_2没有向后滑动,此时第一个窗口和第二个窗口就会有一个元素重合。因此我们多设立一个max_idx12_1,它能保留住上一次循环时第一个窗口的位置。在不满足max_sum1 + sum2大于max_sum2的情况下,max_idx12_1和max_idx12_2都保留上一次循环的值即可。
max_sum123的计算和位置记录同理,不再赘述。
三个窗口每次循环都向右滑动一格,知道第三个窗口达到数组最右端,循环结束。
代码如下。
//动态规划
class Solution {
public:
vector<int> maxSumOfThreeSubarrays(vector<int>& nums, int k)
{
int sum1 = 0, sum2 = 0, sum3 = 0;
int max_sum1 = 0, max_sum12 = 0, max_sum123 = 0;
int max_idx1 = 0, max_idx12_1 = 0, max_idx12_2 = 0;
int max_idx123_1 = 0, max_idx123_2 = 0, max_idx123_3 = 0;
for (int idx = k * 2; idx < nums.size(); idx++) {
sum1 += nums[idx - 2 * k];
sum2 += nums[idx - k];
sum3 += nums[idx];
if (idx >= 3 * k - 1) {
if (sum1 > max_sum1) {
max_sum1 = sum1;
max_idx1 = idx - 3 * k + 1;
}
if (max_sum1 + sum2 > max_sum12) {
max_sum12 = max_sum1 + sum2;
max_idx12_1 = max_idx1;
max_idx12_2 = idx - 2 * k + 1;
}
if (max_sum12 + sum3 > max_sum123) {
max_sum123 = max_sum12 + sum3;
max_idx123_1 = max_idx12_1;
max_idx123_2 = max_idx12_2;
max_idx123_3 = idx - k + 1;
}
sum1 -= nums[idx - 3 * k + 1];
sum2 -= nums[idx - 2 * k + 1];
sum3 -= nums[idx - k + 1];
}
}
return {max_idx123_1, max_idx123_2, max_idx123_3};
}
};
滑动窗口方法的时间复杂度为O(n),比动态规划算法要快许多。