DATASET CONDENSATION WITH GRADIENT MATCHING

ABSTRACT

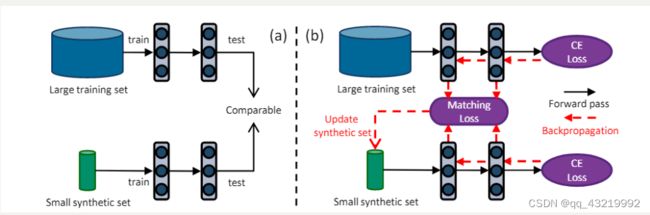
This paper proposes a training set synthesis technique for data-efficient learning, called Dataset Condensation, that learns to condense large dataset into a small set of informative synthetic samples for training deep neural networks from scratch.

本文提出了一种用于数据高效学习的训练集合成技术，称为数据集压缩，它学习将大型数据集压缩成一小组信息丰富的合成样本，用于从头开始训练深度神经网络.

1.INTRODUCTION

We formulate this goal as a minimization problem between two sets of gradients of the network parameters that are computed for a training loss over a large fixed training set and a learnable condensed set

我们将此目标表述为网络参数的两组梯度之间的最小化问题，这些梯度是针对大型固定训练集和可学习的浓缩集的训练损失计算的

2.METHOD

2.1 DATASET CONDENSATION

$$\begin{gathered} largedataset:\tau \\ \tau :(x_i,y_i){|}_i^{\tau } \\ deepneuralnetworkwith\theta :\varphi \end{gathered}$$

Our goal is to generate a small set of condensed synthetic samples with their labels: S
$$S:(x_i,y_i){|}_i^S$$

Discussion

​ pose the parameters θS as a function of the synthetic data S
$$S^{\ast }=\underset{S}{a}rgmin{\mathcal{L}}^{\tau }({\theta }^S(S))subjectto{\theta }^S(S)=\underset{\theta }{a}rgmain{\mathcal{L}}^S(\theta )$$
​ Issue:

​ requires a computationally expensive procedure and it does not scale to large models

---

2.2 DATASET CONDENSATION WITH PARAMETER MATCHING

​ we aim to learn S such that the model ${\varphi }_{{\theta }^S}$ trained on them achieves not only comparable generalization performance to ${\varphi }_{{\theta }^{\tau }}$ but also converges to a similar solution in the parameter space (i.e. ${\theta }^S={\theta }^{\tau }$ )

我们的目标是学习 S 使得在它们上训练的模型 ${\varphi }_{{\theta }^S}$ 不仅实现了与 ${\varphi }_{{\theta }^{\tau }}$相当的泛化性能，而且在参数空间（即 ${\theta }^S={\theta }^{\tau }$ ）中也收敛到类似的解决方案

​ Now we can formulate this goal as
$$\underset{S}{m}inD({\theta }^S,{\theta }^{\tau })subjectto{\theta }^S(s)=\underset{\theta }{a}rgmin{\mathcal{L}}^S(\theta )\text{\hspace{1em}(4)}$$
​ In a deep neural network,$ \theta^\tau$ typically depends on its initial values ${\theta }_0$. However, the optimization in $eq.$ (4) aims to obtain an optimum set of synthetic images only for one model ${\phi }_{{\theta }^{\tau }}$ with the initialization ${\theta }_0$, while our actual goal is to generate samples that can work with a distribution of random initializations ${\mathrm{P}}_{{\theta }_0}$,Thus we modify $eq.$(4) as follows

在深度神经网络中，${\theta }^{\tau }$ 通常取决于其初始值 ${\theta }_0$。但是，等式4中的优化旨在仅针对初始化 ${\theta }_0$ 的模型 ${\phi }_{{\theta }^{\tau }}$ 获得一组最佳合成图像，而我们的实际目标是生成可以使用随机初始化分布 ${\mathrm{P}}_{{\theta }_0}$的样本,所以我们对公式4进行修改

$$\underset{S}{m}in{\mathrm{E}}_{{\theta }_0\in {\mathrm{P}}_{{\theta }_0}}[D({\theta }^S({\theta }_0),{\theta }^{\tau }({\theta }_0))]subjectto{\theta }^S(S)=\underset{\theta }{a}rgmin{\mathcal{L}}^S(\theta ({\theta }_0))\text{\hspace{1em}(5)}$$

​ As the inner loop optimization ${\theta }^S(s)=\underset{\theta }{a}rgmin{\mathcal{L}}^S(\theta )$ can be computationally expensive,adopt the back-optimization approach which re-defines ${\theta }^S$ as the output of an incomplete optimization

由于内环优化${\theta }^S(s)=\underset{\theta }{a}rgmin{\mathcal{L}}^S(\theta )$的计算成本可能很高所以redefine ${\theta }^S$

$${\theta }^S(S)=opt-al{g}_{\theta }({\mathcal{L}}^S(\theta ),\zeta )$$

​ $opt-alg$ is a specific optimization procedure with a fixed number of steps (ς)

Discussion

​ ${\theta }^{\tau }$ for different initializations can be trained first in an offline stage and then used as the target parameter vector in $eq.$(5).

​ Issue:

• distance between ${\theta }^{\tau }$ and intermediate values of ${\theta }^S$ can be too big in the parameter space with multiple local minima traps along the path and thus it can be too challenging to reach

  ${\theta }^{\tau }$ 与 ${\theta }^S$ 的中间值之间的距离在沿路径具有多个局部最小值陷阱的参数空间上可能太大，因此到达可能太具有挑战性

• $opt-alg$ involves a limited number of optimization steps as a trade off between speed and accuracy which may not be sufficient to take enough steps for reaching the optimal solution.

  $opt-alg$ 涉及有限数量的优化步骤作为速度和准确性之间的权衡，这可能不足以采取足够的步骤来获得最优解

---

2.3 DATASET CONDENSATION WITH CURRICULUM GRADIENT MATCHING

​ we wish ${\theta }^S$ to be close to not only the final ${\theta }^{\tau }$ but also to follow a similar path to ${\theta }^{\tau }$ throughout the optimization. While this can restrict the optimization dynamics for θ, we argue that it also enables a more guided optimization and effective use of the incomplete optimizer

我们希望 ${\theta }^S$ 不仅接近最终的 ${\theta }^{\tau }$，而且在整个优化过程中也遵循与 ${\theta }^{\tau }$ 相似的路径。虽然这可以限制 θ 的优化动态，但我们认为它也可以更有效地优化和有效使用不完整的优化器

​ now decompose $eq.$ (5) into multiple subproblems:

​ where T is the number of iterations, ${\zeta }^S$ and ${\zeta }^{\tau }$ are the numbers of optimization steps for ${\theta }^S$ and${\theta }^{\tau }$ respectively.

​ In words, we wish to generate a set of condensed samples S such that the network parameters trained on them (${\theta }_t^S$ ) are similar to the ones trained on the original training set (${\theta }_t^{\tau }$ ) at each iteration t.

我们希望生成一组浓缩样本 S，使得在它们上训练的网络参数 (${\theta }_t^S$ ) 类似于每次迭代 t 的原始训练集 (${\theta }_t^{\tau }$ ) 上训练的网络参数。

​ update rule:

​ where ${\eta }_{\theta }$ is the learning rate. Based on our observation $D({\theta }_t^S,{\theta }_t^{\tau })$ ≈ 0), we simplify the formulation in $eq. $(7) by replacing ${\theta }_t^{\tau }$ with ${\theta }_t^S$ and use θ to denote ${\theta }^S$ in the rest of the paper.

用上式简化eq.7，得eq.9

​ We now have a single deep network with parameters θ trained on the synthetic set S which is optimized such that the distance between the gradients for the loss over the training samples ${\mathcal{L}}^{\tau }$ w.r.t. θ and the gradients for the loss over the condensed samples ${\mathcal{L}}^S$ w.r.t. θ is minimized. In words, our goal reduces to matching the gradients for the real and synthetic training loss w.r.t. θ via updating the condensed samples.

我们现在有一个深度网络，其参数 θ 在合成集 S 上进行训练，经过优化，使得训练样本 ${\mathcal{L}}^{\tau }$ w.r.t. θ 上的损失梯度与压缩样本 ${\mathcal{L}}^S$ w.r.t. θ 上的损失梯度之间的距离最小化。换句话说，我们的目标是通过更新压缩样本来减少真实和合成训练损失的梯度w.r.t. θ。

​ This approximation has the key advantage over $eq.5$that it does not require the expensive unrolling of the recursive computation graph over the previous parameters {${\theta }^0$, . . . , ${\theta }^{t-1}$}. The important consequence is that the optimization is significantly faster, memory efficient and thus scales up to the state-of-the-art deep neural networks (e.g. $ResNet$ ).

这种近似比 $eq.5$具有关键优势. 它不需要递归计算图相对于先前参数 {${\theta }^0$, . . . , ${\theta }^{t-1}$}。重要的结果是优化速度明显更快、内存效率更高，因此可以扩展到最先进的深度神经网络（例如 $ResNet$ ）。

Discussion

​ Issue:

​ in our experiments we learn to synthesize images for fixed labels, e.g. one synthetic image per class

in our experiments we learn to synthesize images for fixed labels, e.g. one synthetic image per class

Algorithm

Gradient matching loss

A,B两个网络计算distance的一种方法，详细见论文