过程参数仪表与检测课后作业&知识点总结

pdf背诵版本的下载地址: 过程参数仪表与检测课后作业&知识点总结（访问密码：3834）

若发现内容有误请在下方评论区留言

# 绪论

1. 流量测量系统由0.5级一次装置,0.25级差压变送器,1.6级开方器,0.5级显示器组成,求:

   1. 该系统的精度等级γ
   2. 流量测量范围300~1200t/h的允许误差$\delta y_u$
   3. 用户与供方仪表均相同,问流量值相差多少时,两套装置可能均合格

   解:

   1. $\gamma =\sqrt{{\gamma }_1^2+{\gamma }_2^2+{\gamma }_3^2+{\gamma }_4^2}=1.7671$
   2. $\delta y_u=\pm \gamma \%\times A=\pm 1.7671\%\times (1200-300)=\pm 15.9t/h$
   3. $|\delta {|}_{max}=2|\delta y_u|=31.8t/h$

第一章 温度测量

若发现内容有错误请在底部留言区留言,我看见了就修改. 也请关注下方留言区勘误,以防修改不及时

温标

1. 说明华氏温标内容,意义及存在的局限性

   • 内容: 华伦海特以水银为介质,以当地最低气温为0,以正常人的体温为96,将温度变化引起的水银柱高程变化分为96等分,每一份为一度.

   • 意义: 首次做出了可以粗略量化温度的器具,有了"一份"的概念

   • 局限性:

     1. 不准确: 因为每年的最低气温不一定相同,因此很不准确
     2. 依赖于物质,不科学,度的概念混乱
     3. 不能复现,例如:定义0°C时,每天的水银柱页面不一定在同一处

2. 说明摄压温标的内容,意义以及存在的局限性

   • 内容: 摄阿西斯规定1个大气压下, 水的凝固点为0度,沸点为100度,中间分为100等分,每分为1°C

   • 意义: 对0~100度重新定义,能复现温度的准确性

   • 局限性:

     1. 范围受物质相变点的限制,上限500°C(水银汽化点),下限水银凝固点
     2. 实际物质的膨胀不是线性的,不同温度的膨胀度不同

3. 不同温度标尺对比如图表所示,以定容氢气体温度计为参照,说明摄氏温标铂电阻温标,铂铑-铂电阻温标出现不同物理量的原因,从而进一步说明摄氏温标的局限性.

   定容氢气体温度计	铂电阻温度计	铂铑-铂热电偶	水银温度计
   0	0	0	0
   20	20.240	20.150	20.091
   40	40.360	40.293	40.111
   60	60.360	60.293	60.086
   80	80.240	80.147	80.041
   100	100	100	100

   1. 实际物体的膨胀并非是线性的,依赖于物质“度”的概念不能准确复现,不科字,不统一,不准确.
   2. 温标的扩展仍受物质限制,无法满足生产科研的需求.

4. 绝对温标/热力学温标的内容,局限性

   以热力学第二定律为基础的热力学温标,与物质的性质无关$T=\frac{Q}{Q_{100}-Q_0}\times 100\%$

   局限性: 卡诺热机理想状态下不存在,实际使用时仍需要一定的修正

5. 实用温标的内容,意义

   内容: 国际标准化组织给出规定了17种标准物度的相变点,温度,在固定点上分度的标准.内插仪器作为基础,固定点之间的温度,由内插公式确定.

   意义: 实用温标精准地复现了热力学温标.

若发现内容有错误请在底部留言区留言,我看见了就修改. 也请关注下方留言区勘误,以防修改不及时

接触式测温方法

热电偶温度计

热电现象

1. 热电偶回路: 把两种不同的导体两端接成闭合回路,两接点分别位于$T$,$T_0$温度下($T>T_0$).回路中产生的热电势由接触电势和温差电势两部分组成

   

2. 热电势

   • 接触电势: 由于两种不同导体的自由电子密度不同而在接触处形成的电动势.

     $$e_{AB}(T)=\frac{kT}{e}\ln \frac{N_A(T)}{N_B(T)}$$
     其中$k$表示玻尔兹曼常数,$e$表示电子电量

   • 温差电势

     $$e_A(T,T_0)=\frac{k}{e}{\int }_{T_0}^{T}d(N_{A}t)$$

   • 热电偶回路总电势

     $$E_{AB}(T,T_0)=e_{AB}(T)+e_B(T,T_0)-e_{AB}(T_0)-e_A(T,T_0)$$

热电偶测温的三个基本定律

1. 三个基本定律的内容: 均质导体定律,中间导体定律,中间温度定律

   1. 均质导体定律: 由一种均质导体组成的闭合回路,不论导体的截面和长度如何,不论其温度如何分布,都不可能产生热电势.

      其意义如下:

      1. 回答了何种材料才能作为热电偶的测温电极材料:热电偶必须由两种不同的金属组成,每一个称为热电极测温材料
      2. 构成热电偶的热电极材料必须为均质材料,否则会产生无法预知的附加误差
      3. 可以用来检测热电偶电极材料的均匀性(如何检测?加电流计,闭合回路,局部加热)

   2. 中间导体定律: 在热电偶中,只要中间导体两端温度相同,接入中间导体后,对热电偶回路中的总热电势没有影响.

      其意义如下:

      1. 为热电偶热电势的正确测量提供了理论依据
      2. 可以导出参比电极定律,使热电偶的选配工作大大简化
         (参比电极定律: 如果两种导体A,B对另一种参考导体C的热电势为已知,则这两种导体组成的热电偶的热电势是他们对参考导体热电势的代数$E_{AB}=E_{AC}+E_{CB}$)

   3. 中间温度定律(连接导体定律): 在热电偶回路中,如果热电极A和B分别与连接导线A’和B’相接,其接点温度为$T_1$,$T_n$和$T_0$,如图所示,则回路的总热电势等于热电偶的热电势$E_{AB}(T_1,T_n)$之代数和,这称为连接导体定律,即$E_{AB{B}^{\prime }{A}^{\prime }}(T_1,T_n,T_0)=E_{AB}(T,T_n)+E_{A^{\prime }{B}^{\prime }}(T_n,T_0)$.

      

      其意义如下:

      1. 为热电偶补偿导线的使用提供理论依据: 在1~100°C之间,$A^{\prime }$与$A$,$B^{\prime }$与$B$热点特性相同或相近,将$A^{\prime }$,$B^{\prime }$作为贵重材料$A$,$B$的延长线使用,将大大节省设备投资,$A^{\prime }$,$B^{\prime }$称为$A$,$B$的补偿导线.
      2. 热电偶参比端温度非0°C情况下提提供理论依据

2. 证明三个基本定律

   1. 证明均质导体定律

      • 热电偶的电势由接触电势和温差电势构成
        • 由于材料相同,没有接触电势
        • 而温差电势为大小相同,方向相反的两个电势,相互抵消
      • $E_{AA}(T,T_1,T_2,...,T_n)=\frac{k}{e}{\int }_{T_0}^T\ln \frac{N_A(T)}{N_A(T)}dt=0$

   2. 证明中间导体定律:
      $$\begin{array}{rl}{E}_{AB}(T,T_0)& =e_{AB}(T)+e_B(T,T_0)+e_{BC}(T)+e_C(T,T_0)-e_{AC}(T)-e_A(T,T_0)\\ & =[e_{AB}(T)+e_B(T,T_0)-e_{AB}(T0)-e_A(T,T_0)]+[e_{AB}(T_0)+e_{BC}(T_0)-e_{AC}(T_0)]\\ & =E_{AB}+\frac{kT}{e}\ln \frac{N_B(T)}{N_C(T)}\frac{N_A(T)}{N_B(T)}/\frac{N_A(T)}{N_C(T)}\\ & =E_{AB}\end{array}$$

   3. 证明连接导体定律或中间温度定律

      

3. 计算题

   图示热电偶,其材料如下:A-镍铬; B-镍硅; C-康铜; D-镍铬. 求回路热电势?

   

   解: AB组成K型热电偶,CD组成E型热电偶,计算过程如下
   $$\begin{array}{rl}{E}_{AB}(35.3,50)& =E_{AB}(35.3,0)-E_{AB}(50,0)\\ & =[1.203+\frac{35.2-30}{10}(1.612-1.203)]-2.023=-0.6032mV\\ E_{CD}(50,20)& =E_{CD}(50,0)-E_{CD}(20,0)\\ & =3.048-1.192=1.856mV\\ E_{ABCD}(35.3,20)& =E_{AB}(35.3,50)+E_{CD}(50,20)=1.2528mV\end{array}$$

标准化热电偶

1. 标准化热电偶的定义及其与非标准化热电偶的本质区别

   标准化热电偶是指工艺上比较成熟,能批量生产,性能稳定,应用广泛,具有统一分度表并已列入国际和国家标准文件的热电偶
   本质区别: 标准化热电偶可以互换,精度有一定保证,并有配套的显示,记录仪表

2. 工业用标准化热电偶:(千万要记得分度号)

   1. 铂铑10-铂热电偶(分度号S)
      • 测温范围: 长期使用可达1300°C 短期使用可达1600°C
      • 适用场合: 宜在氧化性和中性气氛中长期使用,可在真空中短期使用,不能在还原性气氛及含有金属或非金属蒸气中使用,除非套有合适的非金属保护套管
      • 特点: 精度高,热电势较小,灵敏度低,高温下机械强度下降,对污染敏感,材料昂贵.
   2. 铂铑13一铂热电偶(分度号R)
      • 综合性能与S型热电偶相当,但稳定性,复现性均好于S型热电阻
   3. 铂铑30一铂铑6热电偶(分度号B)
      • 测温范围: 长时间可达1600°C,短期可达1800°C
      • 适用场合: 适用于氧化性和情性气氛中,可短期用于真空,不可用于还原性气氛或含有金属或非金属蒸汽气氛中
      • 特点: 精度高,稳定性好,测温温区宽,寿命长,参比端无需冷端补偿,灵敏度低,高温下机械强度下降,抗污染能力差,昂贵
   4. 镍铬-镍硅热电偶(分度号K)
      • 测温范围: -200°C~1300°C
      • 适用场合: 能用于氧化性和情性气氛中,不能在高温下直接用于硫,还原性或还原氧化交替的气氛中,也不能用于真空
      • 特点: 线性度好,热电势较大,灵敏度高,稳定性和复现性好,抗氧化性强,价格便宜.
   5. 镍铬硅-镍镁热电偶(分度号N)
      • 测温范围: -200°C~1300°C
      • 适用场合: 高温下不能直接用于硫,还原性或还原氧化交替的气氛中,不能用于真空中.
      • 特点: 线性度好,灵敏度较高,稳定性和复现性好,抗氧化性强,便宜.综合性能优于K型热电偶,具有很大应用前景
   6. 镍铬-康铜热电偶(分度号E)
      • 测温范围: -200°C~900°C
      • 适用场合:可用于湿度较大的环境,不能在高温下用于硫,还原性气氛中
      • 特点: 灵敏度最高,稳定性好,抗氧化性高.宜制成热电堆来测量微小温度变化
   7. 铁-康铜热电偶(分度号J)
      • 测温范围: -40°C~750°C,常用于0°C~750°C
      • 适用场合: 可用于真空,氧化,还原和情性气氛中
      • 特点: 线性度好,灵敏度高,稳定性和复现性好,价格便宜.正极为铁,在高温下氧化较快,故测温上限受到限制
   8. 铜-康铜热电偶(分度号T)
      • 测温范围: -200°C~400 C
      • 适用场合: 测量低温-200°C-0°C
      • 特点: 线性度好,热电势大,灵敏度高,稳定性和复现性好,价格便宜

热电偶的冷端补偿问题

1. 为什么要进行热电偶的冷端补偿:

   由$E_{AB}(T,T_0)=\frac{k}{e}{\int }_{T_0}^{T}ln\frac{N_A(t)}{N_B(t)}dt=f(T)-f(T_0)$.可知: 热电偶的热电势的测量不但与热端温度有关,而且与冷端温度有关,通过测量回路热电势来确定测量端温度,必须使冷端温度固定或消除冷端温度变化对回路热电势造成的影响,这就是热电偶冷端补偿的问题

2. 热电偶冷端补偿的几种方法:

   1. 计算法:
      $U=E_{AB}(T,T_0)$,用其他温度表测出 $t_0$,查表得$E_{AB}(T,0)=E_{AB}(T,T_0)+E_{AB}(T_0,0)$,查表求得$T$.

   2. 冰点槽法:
      如果在测温时将热电偶冷端置于0°C下,就不需要进行冷端温度补偿,这时需要设置一个温度恒为0°C的冰点槽.

   3. 补偿电桥法:

      利用不平衡电桥产生的电压表来补偿热电偶冷端温度变化而引起的热电势变化.冷端温度补偿电桥是一个不平衡电桥,其线路如图所示:

      

      热电偶冷端温度由$T_0$上升到$T_0^{\prime }$,温度上升了$\Delta T=T_0^{\prime }-T_0$,热电偶测温回路所输出热电势由$U(T,T_0)=E_{AB}(T,T_0)$减少到$U^{\prime }(T,T_0^{\prime })=E_{AB}(T,T_0^{\prime })$,减少了$\Delta E=E_{AB}(T,T_0)-E_{AB}(T,T_0^{\prime })=E_{AB}(T_0^{\prime },T_0)$

      如果要使显示仪表的值保持不变,显示器仍为T,则,则需要在热电偶回路提供一个补偿电压,使回路热电势保持不变,加上的一个$\Delta E=E_{AB}(T_0^{\prime },T_0)$由补偿电桥提供.其中$R_1$,$R_3$,$R_4$为定值电阻,$R_{cu}$为铜电阻,有$R_{cu}(t)=R_{cu}(t_0)[1+\alpha (t-t_0)]$,其中$R_{cu}(t)$,$R_{cu}(t_0)$分别为所处温度为$t$,$t_0$时铜电阻的阻值.其中$\alpha$为铜电阻的温度系数($\alpha \approx 4.28\times 10^{-3}1{/}^{\circ }C$).

      电阻$R_S=\frac{\alpha (t_0^{\prime }-t_0)}{E_{AB}(t_0^{\prime },t_0)\times 10^{-3}}-1$

3. 计算题: 设计冷端补偿器,配J型热电偶,其平衡温度17°C,完全补偿温度23°C,问:

   1. $R_S$=?
   2. $t_o^{\prime }’$=30°C,求冷端补偿误差
   3. 显示仪表"0"点应设在多少温度值:

   解:

   1. $R_S=\frac{\alpha (t_0^{\prime }-t_0)}{E_{AB}(t_0^{\prime },t_0)\times 10^{-3}}-1=\frac{4.28\times 10^{-3}(23-17)}{(0.6703-0.9118)\times 10^{-3}}-1=105.335\Omega$

   2. 热电偶热电势改变$\Delta E=E_{AB}(20,17)=E_{AB}(20,0)+E_{AB}(17,0)=0.1197mV$
      电桥输出$U_{cd}$

      • $U_{ab}=E\times \frac{(R_4+R_3)\text{//}(R_1+R_2)}{R_s+(R_4+R_3)\text{//}(R_1+R_2)}$
      • $U_{cd}=U_{ab}\times [\frac{R_{cu}}{R_{cu}+R_1}-\frac{1}{2}]$

      将$E=4V$,$R_{cu}(t)=R_{cu}(t_0)[1+\alpha (t-t_0)]=10.128\Omega$代入得到$U_{cd}=0.1204mV$
      故$\Delta U=U_{cd}-E_{AB}(20,17)=0.0007mV$

   3. 17°C时标为0

热电偶的串并联

1. 热电偶正向串联: 总热电势等于多个热电偶电势之和$U=E_{AB}(t_1,t_0)+E_{AB}(t_2,t_0)+...+E_{AB}(t_1,t_0)$

   

   热电偶正向串联组成热电堆,可以提高测量装置的灵敏度,增大信号输出值

2. 热电偶反向串联: 总热电势等于两热电偶电势之差$U=E_{AB}(t_1-t_2)$

   

   热电偶反向串联可以测量两点间微小温差

   1. 思考题: 两个E型热电阻反向串联,输出$U=E_{AB}(t_1,t_2)=5.384mV$,求$\Delta t=t_1-t_2$?
      答: 不能求解,若要求解$\Delta t=t_1-t_2$,必须保证$t_1$,$t_2$其中之一可知.由$E_{AB}(t_1,t_2)=E_{AB}(t_1,0)-E_{AB}(t_2,0)$求得.
   2. 如何测量两点之间微小误差: 用热电偶测出$t_1$,$t_2$温度之一,再用反向串联的热电偶测得$E_{AB}(t_1,t_2)$的值代入公式$E_{AB}(t_1,t_2)=E_{AB}(t_1,0)-E_{AB}(t_2,0)$查表求得另一温度. 若$\Delta t$太小,则可用热电堆测$E_{AB}(t_1,t_2)$

3. 热电偶并联: 总热电势等于多个热电偶电势的平均值$U=\frac{1}{m}[E_{AB}(t_1,t_0)+E_{AB}(t_2,t_0)+...+E_{AB}(t_m,t_0)]$

   

   设置冗余,若某只热电偶损坏,不影响测温

热电阻温度计

电阻温度系数

1. 热电阻温度计原理: 所有导电材料,其电阻值均随所处温度变化而变化.电阻值R(t)与所处温度t有着一一对应的函数关系,称为热电阻的温度特性

2. 电阻温度系数$\alpha$: 定义电阻温度系数为温度每变化1°C,所引起电阻值的相对变化率$\alpha =\frac{1}{R_0}\frac{dR}{dt}$

   金属材料纯度越高,$\alpha$值越大越稳定,反之亦然.

标准化热电阻

1. $P_t$电阻:
   1. 分度号: $P_{t10}$,$P_{t100}$,即0°C时电阻分别为10Ω,100Ω
   2. 测温范围: 用于测量300°C以下温度,准确度高
   3. 测量场合: 测量锅炉给水温度(280°C),排烟温度(140°C),并在13.8033K~961.78°C做基准内插仪.
2. $C_u$电阻:
   1. 分度号: $C_{u50}$,$C_{u100}$,即0°C时电阻分别为50Ω,100Ω
   2. 测温范围: 用于测量0°C~150°C之间温度,线性度高
   3. 测量场合: 测量各种油温,推力瓦温.
3. $N_i$电阻:
   1. 分度号: $N_{i100}$,$N_{i300}$,$N_{i500}$,即0°C时电阻分别为100Ω,300Ω,500Ω
   2. 测温范围: 用于测量-60°C~180°C之间温度,灵敏度高
   3. 测量场合: 测量各种电机,定子线圈温度

热电偶测温与热电阻测温的区别

1. 热电偶输出的是mV级电压信号,最大上百mV级.
   热电阻输出的是Ω级电阻信号,范围几Ω~几百Ω
2. 热电偶的体积质量可以制作得很小,动态响应性能好.可以测量点温或变化较快的介质温度(动态测温)
   热电阻体积质量较大,所测得温度为所处空间平均温度
3. 热电偶测温上限1800°C,非标准化热电偶测温上限>2000°C
   热电阻测温范围13.8033K~961.78°C,工业上用来测量500°以下温度
4. 热电阻精度可达到最高水平,可以用作基准内插仪
5. 热电偶反向串联,可测点温差
   热电阻构成差动桥路,可测区间温差
6. 热电偶测温要进行冷端补偿
   热电阻测温要考虑连接导线电阻随所处环境变化而变化

若发现内容有错误请在底部留言区留言,我看见了就修改. 也请关注下方留言区勘误,以防修改不及时

非接触式测温方法

接触式测温方法的讨论

1. 什么是接触式测温方法
   将测温元件插入♂被测介质,当传感器与被测介质达到热力学平衡时,传感器的温度(或测温的温度)t作为被测介质温度t_g的测量值.

2. 非接触式测温方法
   传感器不必与被测介质达到热力学平衡,即可获取被测介质(物体)的温度.可以进行遥测或实时测量温度变化剧烈的被测对象动态温度测量.

3. 接触式测温方法的讨论:

   1. 传感器与被测介质达到热力学平衡,传感器温度作为被测介质的温度测量值,测温上限即为传感器材料的耐温限值.
   2. 由于冷壁的存在,使高温烟气的测量值t永远小于实际值t_g,使测温失效
   3. 动态测温误差存在,测温管对温度的响应需要时间,达到热力学平衡,传感器质量越大,所需响应时间越长.

4. 非接触式测温方法的物理学基础: 黑体辐射的普朗克定律

   凡高于0K的物体,都会向四面八方发出辐射,设辐射温度为T的黑体在波长为$\lambda$附近单位面积上发出的辐射记为$E_{b\lambda }(T)$,由维恩公式:
   $$E_{b\lambda }(T)=C_1{\lambda }^{-5}{\left(e^{\frac{C_2}{\lambda T}-1}\right)}^{-1}$$
   若将$E_{b\lambda }(T)$测出,固定$\lambda$值,此时$T=f\left[B_{b\lambda }(T)\right]$,可得$T$值.

5. 物体表面光谱发射率${\epsilon }_{\lambda }$

   ${\epsilon }_{\lambda }=\frac{E_{\lambda }}{E_{b\lambda }}$,即实际物体的光谱辐射率与黑体的光谱辐射率之比.

   黑体: 能吸收外来全部电磁辐射的物体${\epsilon }_{\lambda }=\epsilon =1$
   灰体: 对热辐射只能吸收一部分而反射其余部分的物体${\epsilon }_{\lambda }=\epsilon =C<1$
   选择性辐射体: 其光谱发射率随波长而变化,且${\epsilon }_{\lambda }<1$

6. 非接触式测温方法的种类

   非接触式测温方法	温度计
   亮度平衡测温方法	光学温度计,光电高温计
   全辐射测温方法	全辐射温度计
   比色测温方法	比色温度计

7. 比较三种非接触测温方法的优缺点,分析其测温结果的精度

   1. 亮度平衡测温法
      • 优点: 结构简单,灵敏度高,准确度高,响应快
      • 缺点: 测量结果易受到物体光谱发射率变化及中间介质吸收的影响
   2. 全辐射测温方法
      • 优点: 自动测温,输出量为电量
      • 缺点: 灵敏度低,测量结果更易受物体发射率变化及中间介质吸收的影响
   3. 比色测温方法.
      • 优点: 灵敏度高,在中高温范围内效果好,测温结果受物体发射率及中间介质吸收的影响小
      • 缺点: 结构较复杂,价格昂贵.

亮度平衡测温方法

1. 亮度平衡测温方法: 比较被测物体与标准参考辐射源在同一波长下的光谱亮度,并使二者的亮度相等,从而确定被测物体温度的一种方法

2. 亮度温度: 温度为T的被测物体在波长为$\lambda$时的光谱亮度$B_{\lambda }$与温度为$T_0$的黑体在同一波长下的光谱亮度$E_{b\lambda }$相等时,黑体温度$T_0$就被称为被测物体的亮度温度,是一种光学条件温度.

3. 亮度平衡测温方法的理论基础,解决方案,技术路线

   1. 原理: 黑体辐射的普朗克定律$E_{b\lambda }(T)=C_1{\lambda }^{-5}{\left(e^{\frac{C_2}{\lambda T}-1}\right)}^{-1}$,亮度与温度之间存在一一对应的关系.

   2. 解决方案:

      1. $B_{b\lambda }(T)$,$B_{\lambda }(T)$如何测量?
         物体的光谱辐射亮度难以测量,可以用一个温度已知,亮度可调的”标准参考辐射源"与被测物体光谱辐射亮度相比较,使二者亮度相等.以标准参考辐射源的亮度作为被测物体的光谱辐射亮度

      2. 实际物体不存在单色光,$\lambda$单位波长间隔如何获取?
         以红外滤光法或干涉滤光法来获取被测物体在该波长范围较窄的光谱段,$\lambda$在0.66~0.67$\mu m$代替单色光

      3. 被测物体多样且无法选择,只考虑被测物体是黑体的情况,实际物体获得其光谱发射率${\epsilon }_{\lambda T}$后进行修正
         $$\frac{1}{T}-\frac{1}{T_b}=\frac{\lambda }{C_2}\ln {\epsilon }_{\lambda T}$$

4. 测量步骤

   

   1. 将测温装置(光学温度计)对准被测物体

   2. 调目镜,看清灯丝

   3. 调物镜,使物体在灯丝所在的平面成清晰的像

   4. 将"K”打在"测量"挡位,调可变电阻R₂的阻值,改变灯丝的亮度,使灯丝完全消失在背景中(此时灯丝亮度$B_{b\lambda }(T_0)$与$B_{b\lambda }(T)$相等)

   5. 读二次仪表温度示值,加上灰色吸收玻璃量程值,得到物体的亮度温度T₁

   6. 待得知${\epsilon }_T$后,由$\frac{1}{T}-\frac{1}{T_1}=\frac{\lambda }{c}\ln {\epsilon }_{\lambda T}$

5. 检测的方框图

   

6. 特点:

   1. 灵敏度高: 1000K~1400K,温度增加了0.4倍,亮度增加了500倍
   2. 原理先进: 是一种闭环式仪表,测量精度是目前人类掌握的超过961.78°C以上的测温最准确的仪表,可作为基准内插仪使用
   3. 灰色吸收玻璃精度影响温度测量的精度
   4. 工作光谱段是可见光谱,一般用在超过900°C的测温对象
   5. 仪表镜头至物体之间的介质影响测温精度(烟气,蒸汽,粉尘等)
   6. 传感器不必同被测对象达到热力学平衡,即灯丝温度不必同被测物体温度相等,理论上不存在测温上限,但由于灯丝熔点限制,一般测温上限为3000°C

全辐射测温方法

1. 全辐射测温方法: 通过比较被测物体与黑体发出的全辐射能,使二者相等,从而获得被测物温度的方法.

2. 全辐射温度: 温度为$T$的物体所发出的全辐射能$E_{\lambda T}={\int }_0^{\infty }{E}_{\lambda }(T)d\lambda$与$T_0$的黑体所发出的全辐射能$E_b(T)={\int }_0^{\infty }{E}_{b\lambda }(T)d\lambda$相等时,黑体的温度$T_0$称为被测物体的全辐射温度

3. 全辐射温度计是如何分度的?
   按黑体温度$T=T_P\sqrt[4]{\frac{1}{{\epsilon }_T}}$,$T_p$即为被测物体的辐射温度

4. 画出全辐射温度计的热电堆原理图,说明其工作原理

   

比色测温方法

1. 比色测温方法和比色温度
   当温度为$T$的实际物体在两个波段${\lambda }_1$${\lambda }_2$下的辐射强度之比与温度为$T_{CS}$的黑体在相同波段${\lambda }_1$,${\lambda }_2$下的辐射强度之比相等时,黑体的温度$T_{CS}$即为物体的比色温度

2. 如何分度比色温度计,给出分度方法及步骤

   

红外温度计

1. 红外温度计属于哪种测量方法,适用场合
   非接触测温方法,当工作波长在红外67~1000$\mu m$时用红外温度计.

第二章 显示仪表

若发现内容有错误请在底部留言区留言,我看见了就修改. 也请关注下方留言区勘误,以防修改不及时

动圈表

1. 特征: 悬置在永磁场中的可动线圈

2. 工作原理: 处在永磁场的线圈中有电流,会产生电磁力矩$M=nBIA$,在$M$作用下线圈转动,张丝产生反力矩$M_n=k\phi$,当电磁力矩和反力矩相等时,线圈达到稳定状态圈静止,有$k\phi =nBIA$,则$I=\frac{k}{nBA}\phi$. 将电流转化成转角,完成了对未知电流的测量.

   硅铁形成的柱体的作用: 使气隙中线圈所在平面无论转动到何位置,磁力线都与线圈所在平面平行.

   

3. 动圈表不可替代性: 是作为检测计使用,可以发现回路中微弱电流随时间的变化.(复射式检流计)

若发现内容有错误请在底部留言区留言,我看见了就修改. 也请关注下方留言区勘误,以防修改不及时

电位差计

1. 偏差测量法与零差测量法
   1. 偏差测量法: 传感器或仪表在输入被测物理量的作用下,从初始位置发生位移,终位置与初始位置的偏差表征被测物理量
   2. 零差测量法: 用与被测物理量同性质的,准确已知,连续可调的标准量与输入的被测物理量相比较,当两者差值为0时,已知的标准量作为被测物理量的测量值
2. 电平衡原理
   用准确已知,连续可调的标准电压与输入的被测电压相比较,当两者的差值为0时,用已知的标准电压作为输入电压的测量值

手动电位差计

1. 画出手动电位差计的工作原理图,说明测量原理及过程,画出测量框图

   测量原理: 电平衡原理

   测量过程:

   

   1. K置"标准"档位,调$R_S$使检流计示零,此时有$I_1{R}_N=E_N$,$I_1=\frac{E_N}{R_N}=I_N$,工作电流标准化
   2. K置"测量"档位,调精密滑线电阻$R_{\overline{ABC}}$滑动触电B的位置,使电位计G示零.$I_N=\frac{E_N}{R_N}=\frac{E_X}{R_{\overline{AB}}}$,$E_X=\frac{E_N}{R_N}{R}_{\overline{AB}}=\frac{E_N}{R_N}\alpha \overline{AB}=\phi \overline{AB}$
   3. $\overline{AB}$按电压分度,实现了对$E_X$的测量

2. 手动电位差计测量方框图

   

电子电位差计

1. 画出电子电位差计原理图,说明测量原理及过程,画出测量框图

   

   • 测量过程: A点在$R_p$上滑动改变桥路输出的电压,用$U_{AB}$连续可调准确已知来表征$E_X$,$\Delta U=U_{AB}-E_X$进入伺服放大器,极性与$\Delta U$相同放大进入伺服电机,经机械传动装置改变A的位置,直到$U_{AB}$变至$\Delta U=U_{AB}-E_X=0$为止,此时$U_{AB}=E_X=k\overline{OA}$,可用$\overline{OA}$表征$E_X$

   • 测量方框图

     

2. 电子电位差计$R_M$,$R_B$,$R_P$,$R_P^{\prime }$的作用:

   1. $R_M$: 提高测量量程
   2. $R_B$: 使$R_P\text{//}{R}_B=90\Omega$,提高合格率,降低成本
   3. $R_P$: 精密滑线电阻,A在$R_P$上滑动改变桥路输出电压
   4. $R_P^{\prime }$: 与$R_P$完全相同的精密滑线电阻,为了消除滑点与划线间的寄生电势

3. 为什么采用双滑线结构:

   

   $R_P$,$R_P^{\prime }$为滑动触点(银球)提供了一个滑动轨道,产生的接触电势$e$,$e^{\prime }$等大,反向,消除了触点A与$R_P$,$R_P^{\prime }$的接触电势

4. 冷端补偿如何解决:

   铜电阻$R_{cu}$置于冷端温度$t_0$中,
   $$R_{cu}(t_0)=R_{cu}(0)\left[1+\alpha (t_0-0)\right]$$
   其中$R_{cu}(0)$为$R_{cu}$冷端补偿电阻阻值.

若发现内容有错误请在底部留言区留言,我看见了就修改. 也请关注下方留言区勘误,以防修改不及时

平衡电桥

1. “三线制”接法的连接导线电阻$R_{w3}$变化造成了什么影响?
   $R_{w3}$的变化只影响检流计的灵敏度,其影响可忽略

2. 画三线制“手动平衡电桥的测温原理图

   

3. 图示说明”二线制”手动平衡电桥工作原理及局限性

   • 原理:

     1. 调$R_S$,使A示定值,$I_1=6mA$直流电流

     2. 调$R$,滑动触点$P$,改变$R_{\overline{OP}}$值,使G示“0”.此时电桥平衡

        

   • 局限性

     连接导线$R_{w1}$,$R_{w2}$的阻值随环境温度的变化而变化,易产生附加误差

4. 热电阻测温为什么要用‘三线制接法”?画出电路图说明

   
   

若发现内容有错误请在底部留言区留言,我看见了就修改. 也请关注下方留言区勘误,以防修改不及时

模数转换器(ADC)

1. 某测温系统测温范围300°C~600°C,要求分辨率为0.25°C,应该选用多少位的ADC?
   解:
   $$\frac{600-300}{2^N}\le 0.25$$

   $$N\le 11$$

   工业用ADC有4,8,10,12,16位,故应选12位ADC.

积分式ADC

1. 图示说明双积分式ADC工作原理

   

   工作分为三个周期:

   1. 准备期: $S_1$,$S_2$,$S_3$断开,$S_4$闭合,$C$(积分电容)中的电荷通过$R_1$放掉,此时积分器输出$V_c=0$,输出$V_0=0$.

   2. 采样期: $S_2$,$S_3$,$S_4$断开,$S_1$闭合,将被测的模拟电压$V_i$接到积分器输入端,积分器即对$+V_i$进行积分,$t_1$时刻开始到$t_2$时刻结束,积分时间$T_1=t_2-t_1$,$t_2$时刻积分器输出
      $$V_c=-\frac{1}{RC}{\int }_{t_1}^{t_2}{V}_{i}dt=-\frac{T_1}{RC}\overline{V_i}$$
      其中$\overline{V_i}=\frac{1}{T_1}{\int }_{t_1}^{t_2}{V}_{i}dt$,为被测模拟量在$T_1$期间的平均值

   3. 比较期: 从$t_2$时刻起,$S_1$,$S_2$,$S_4$断开,$S_3$闭合,将与被测模拟电压$V_i$极性相反的标准电压$-E_r$接入积分器,输入端($V_i$为"-”,则$S_2$闭合,其余断开),反向积分直到积分回到0时
      $$0=V_c-\frac{1}{RC}{\int }_{t_2}^{t_3}(-E_r)dt=-\frac{T_1}{RC}\overline{V_i}+\frac{T_2}{RC}\overline{E_r}$$

      $$T_2=T_1\frac{\overline{V_i}}{E_r}$$

      $T_2$表征被测电压$V_i$,完成了对$V_i$的测量

2. 如何理解积分式ADC对已知频率的干扰信号有无穷的抑制力?图示说明

   

   交流干扰$U_x$与被测信号$Vx$同频率串联,称为串模干扰

   在采样周期内,对$U=V_x+U_x$积分,积分时间设定为$U_x$周期的整数倍
   $${\int }_{\square }={\int }_0^{n{T}_0}[V_x(t)+U_x(t)]=\overline{V_X}\cdot T$$
   这样就消除了$U_x$对测量的影响

3. 分析双积分式ADC的局限性
   解: 工频干扰以$f=50Hz$为基波,因此积分时间$T=n\frac{1}{f}=n\cdot 20ms$.可见双积分式ADC响应慢,响应时间为ms级

阶梯波比较式ADC

第三章 压力仪表

1. 1mm水柱,1mmHg柱所形成的压力各自是多少
   解:
   $$\begin{gathered} P_{水}={\rho }_{水}gH=1.0\times 10^3\cdot 9.8\cdot 1\times 10^{-3}=9.8Pa \\ {P}_{Hg}={\rho }_{Hg}gH=13.6\times 10^3\cdot 9.8\cdot 1\times 10^{-3}=133.28Pa \end{gathered}$$

2. 简述大气压力,全压力(绝对压力),表压力,真空压力

   大气压力: 地球表面大气柱形成的压力随时间,地点有所变化
   绝对压力: 作用在物体表面上的全部压力(包括大气压力),其零点为绝对真空.绝对压力=大气压+表压
表压力/相对压力: 以大气压力作为基准所表示的压力.
   真空压力=绝对压力-大气压力
表压力: 高于大气压力时的绝对压力与大气压力之差

   真空度(负压)是绝对压力与低于大气压力时的绝对压力差

   

若发现内容有错误请在底部留言区留言,我看见了就修改. 也请关注下方留言区勘误,以防修改不及时

压力测量方法

1. 弹性元件输入,输出关系如图,为什么要求弹性元件工作在弹性形变区?

   

   弹性形变区,压力与弹性基本呈现线性关系,而塑性形变区线性度差,不便测量

2. 压力的测量方法有哪些?

   1. 弹性力平衡法:
      弹性元件受到压力而产生变形,弹性力与被测压力相平衡,测出其变形的位移就可测出弹性力.例如弹簧管压力计,波纹管压力计,膜式压力计.
   2. 重力平衡法:
      活塞式压力计: 将压力转化成砝码质量来进行测量
      液柱式压力计: 将压力转化为液柱高度进行测量
   3. 机械力平衡法: 将被测压力变换为一个集中力,用外力与之平衡来测压
   4. 物性测量方法: 基于有压力作用下,测压元件的某些物理特性发生变化的原理,如电气压力计,振频式压力计,光纤压力计,集成式压力计

3. 常用的压力敏感元件有哪些?画出上述元件输入-输出特性曲线

   
   平膜片,波纹膜片,弹簧管,波纹管膜盒

若发现内容有错误请在底部留言区留言,我看见了就修改. 也请关注下方留言区勘误,以防修改不及时

压力传感器与变送器

电容式压力传感器

1. DPHP1151电容式压力传感器变送器的工作原理
   感压膜片受$\Delta P=P_H-P_L$作用,产生位移$\Delta d$,位移的变化改变了电容式传感器的电容输出,将电容变化的信号进行处理,可得到4~ 20mA直流电流输出,输出电流值表征被测压力.

2. DP HP电容式压力(差压)变送器选择处理的信号是什么信号?为何选取该信号进行处理?

   处理的信号是$\frac{C_L-C_H}{C_L+C_H}=\frac{\Delta d}{d_0}=k\cdot \Delta P$

   原因:

   1. $\frac{C_L-C_H}{C_L+C_H}=k\cdot \Delta P$,与输入压差成正比,不存在非线性误差
   2. 不存在${\epsilon }_r$,${\epsilon }_0$项,消除了传感器充液介电常数随温度变化对测量造成的影响
   3. 正负压差完全对称,消除了静压误差

扩散硅压力传感器

1. 讨论金属材料和半导体材料作为压力传感器的优势和局限性
   金属材料: 材料易得,结构简单; 但体积大,需要与弹性膜片粘贴受温度影响
   半导体材料:灵敏度高; 但受温度影响,工艺要求高

2. 扩散硅压力传感器与变送器工作原理
   答:感压元件硅膜片受被测压力P的作用,产生应变$\epsilon$,$\epsilon$与P存在固定函数关系$P=f(\epsilon )$.在感压硅膜片(掺杂半导体)扩散的电阻与感压膜片属性相反,产生应变,扩散电阻根据所在位置应变的属性,阻值增(减),将扩散电阻接成差动桥路/恒流激励输出电压信号,经变送器电路处理转化为4~20mADC或1~5VDC输出

3. 作业3:扩散硅压力传感器输出电阻应如何连接?
   答:差动桥路

   

4. 作业4:为消除温度变化对测压的影响,如何连接扩散电阻
   答:同上图,可消除温度变化的影响

5. 作业5:扩散硅压力传感器的感压元件是什么?
   答:感压硅膜片,掺杂有半导体

6. 如何布置扩散电阻

   • $R$在0.635$r_0$之内,感受拉应力,阻值变大
   • $R$在0.635$r_0$之外,感受压应力,阻值变小

   为消除温度变化对压力测量的影响,获得高测量灵敏度,将$R_2$,$R_3$布置在0.635$r_0$之内,感受拉应力,阻值变大;将$R_1$,$R_4$布置在0.635$r_0$之外,感受压应力,阻值变小,将$R_1$,$R_2$,$R_3$,$R_4$接成差动桥路,达到上述目的.

   

若发现内容有错误请在底部留言区留言,我看见了就修改. 也请关注下方留言区勘误,以防修改不及时

压力测量仪表注意事项

1. 如何选择压力表的量程:

   1. 若被测压力稳定,则测量上限值为量程的$\frac{2}{3}$

      $\frac{2}{3}\times 量程=最大测量压力$

   2. 若被测压力变化大,则测量上限值为量程的$\frac{1}{2}$

      $\frac{2}{3}\times 量程=最大测量压力$

2. 压力计的零点迁移方法:
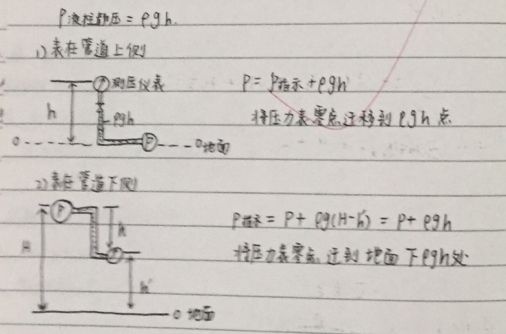
   测量的目的是测压仪表显示管路内流体压力值$P$,当取压口位置与测压仪表(传感器)不在同一平面上,需要消除关内流体形成的静压力$P_{液柱静压}=\rho gh$

   

   1. 表在管道上侧:
      $P_{真实压力}=P_{指示}+\rho gh$
      将压力表零点迁移到$\rho gh$点
   2. 表在管道下侧
      $P_{指示}=P_{真实压力}+\rho g(H-h^{\prime })=P_{真实压力}+\rho gh$
      将压力表零点迁移到$-\rho gh$点

3. 取压口位置选择:

   1. 被测介质为液体: 取压口选在侧下方,防止气塞或取压管道进入固体杂质

      

   2. 被测介质为气体: 取压口选在侧上方,防止液塞或取压管道进入固体杂质

      

   3. 被测介质为水蒸气: 取压口轴线垂直于工艺管道侧壁,内壁光滑无毛刺

      

第四章 流量测量

1. 流量的定义,体积流量,质量流量
   流量的定义: 单位时间内,通过固定截面的流体的质量
   体积流量: $q_v=\frac{dv}{dt}$
   质量流量:$q_m=\frac{dm}{dt}$
2. 流量的测量方式:
   1. 容积式: 椭圆齿轮流量计,腰轮流量计,气体钟罩
   2. 速度式: 通过测量管道截面上流体的平均流速$\overline{v}$,得到$q_v=\overline{v}A$
   3. 质量式: 直接质量式,基于科里奥利力的质量流量计,热式质量流量计,托马斯气体流量计

若发现内容有错误请在底部留言区留言,我看见了就修改. 也请关注下方留言区勘误,以防修改不及时

容积式流量计

1. 腰轮流量计工作原理

   

   两个紧密啮合的腰轮在流体的推动下,绕各自的固定轴转动,各带一个齿轮$O_1$,$O_2$与腰轮同轴,其中$O_1$,$O_2$交替提供力矩,使齿轮转动,每转动$2\pi$向下游排除4份空腔内流体体积.作用在$O_1$上的综合力矩
   $$M_{O1}=(P_{+}\cdot \frac{S}{4}-P_{+}\cdot \frac{S}{4})l+(P_{-}\cdot \frac{S}{4}-P_{-}\cdot \frac{S}{4})l=0$$
   作用在$O_2$上的综合力矩
   $$M_{O2}=(P_{+}\cdot \frac{S}{4}-P\cdot \frac{S}{4})l+(P_{-}\cdot \frac{S}{4}-P\cdot \frac{S}{4})l=(P_{+}-P_{-})\cdot \frac{S}{4}l\ne 0$$

   此时$O_2$带动$O_1$转动,$\frac{\pi }{2}$后,$O_1$带动$O_2$转动,每隔$\frac{\pi }{2}$后,$O_1$,$O_2$相互转换,相互提供转动力矩.
   只需对腰轮转数计数,计数值即可表征流体总体积流量.

若发现内容有错误请在底部留言区留言,我看见了就修改. 也请关注下方留言区勘误,以防修改不及时

速度式流量计

1. 截面上的平均流速,直径上的平均流速,弦上的平均流速的概念

   • 截面上的平均流速: 流线顶端抛物线围成的体积与同截面圆柱体积相等时,圆柱体的高度可看成截面上的平均流速$\overline{v}$,如图所示:
     
     需要补充
   • 直径上的平均流速: 在以直径为底的纵切面上,流线顶端抛物线围成的面积与同底矩形面积相等时,矩形的高度可看成直径上的平均流速$\overline{v_D}$,即$v_D\cdot D={\int }_0^{D}v(r)dr$
   • 弦上的平均流速: 在以弦为底的纵切面上,流线顶端抛物线围成的面积与同底矩形面积相等时,矩形的高度可看成弦上的平均流速$\overline{v_L}$,即$v_L\cdot L={\int }_0^{L}v(r)dr$
     

涡轮流量计

1. 涡轮流量计的工作原理,特点
   • 工作原理: 安装在被测管道中零功率输出的涡轮机,流体流动与涡轮叶片相互作用,驱动涡轮转动,涡轮转速$n$正比于流体流速$v_0$,测出$n$可得$v_0$,进而得$q_v=A\cdot \overline{v}$
   • 适用流体: 单相流体,气体,液体,水蒸气; 可用于脉动流
   • 特点
     1. 适用流体:单相,清洁
     2. 速度式,对直管段要求前15D,后5D
     3. 受流体粘度变化影响大
     4. 流体温度一般不超过300℃(铁磁材料的居里温度)
     5. 轴承的寿命决定仪表的寿命
     6. 数字式输出,信号处理方便
2. 由仪表数$\xi$随流量变化曲线给出涡轮流量计的范围度
   答:$\xi -q_v$曲线中只有前20%近似线性,因此范围度Sc=5:1
   
3. 分析$\xi$不是一条水平线的原因(从流体流速变化及与涡轮转动阻力关系出发进行分析)
   答:流速的变化与涡轮转动阻力有关,层流到紊流的过渡区的流动阻力最小.小流量时,各种阻力对叶轮转速影响大,故$\xi$值较小;过渡区$\xi$出现先增大再减小,大流量时,各种阻力影响又相对增大,$\xi$值减小
4. 涡轮流量计测得的是何种流速
   答:速度式流速

涡街流量计

1. 涡街流量计工作原理: 卡曼涡街现象
   流体在与流速垂直的方向(横向)上产生振动
   需要补充
   
   $R_{el}>60$时,出现涡街,$R_{el}>10^7$时,涡街稳定
   单侧涡街产生的频率$f=S_t\frac{v}{L}$
   涡街稳定条件: $S_h\frac{\pi h}{L}=1$,$\frac{h}{L}=0.281$
   测出涡街频率$f$,即可求得流速$v$,从而得到流量
2. 单侧漩涡频率检测方法
   1. 检测热线法:
      流体横向振动,冲刷流体检测线,$R_t$温度比流体高10~20°C,$R_t$阻值呈现规律性变化,频率即为单侧漩涡产生的频率.
      总能量守恒$\frac{1}{2} \rho (v-u)^2 + p_{j上} = \frac{1}{2} \rho (v-u)^2 + p_{j下} $
      
   2. 压电晶体法
      
3. 涡街流量计的特点:
   1. 数字量输出
   2. 流量测量不受流体温度,压力,密度,粘度的影响
   3. 测量范围宽
   4. 管道内径大
   5. 压力损失小
   6. 适用于单相工质
   7. 直管段要求: 上游20D,下游$\ge$ 0.5D

电磁流量计

1. 电磁流量计工作原理: 法拉第电磁感应定律
   
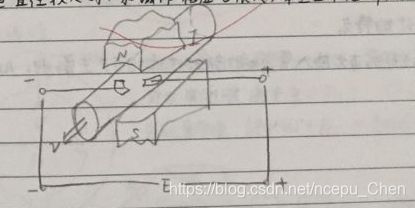
   导体的流体在管道内流动切割磁力线,在于流体流速垂直的方向上,产生感应电动势$E$,与流体速度$v$成正比,测出$E$可求$v$,进而求得$q_v=A\cdot v$,完成对管内流体的实时测量.
   适用流体: 导电液体
2. 为什么采用交变磁场
   直流磁场产生的$E$方向固定,正负离子吸附负正电极,导致$E$下降,在极板上发生电化学反应,腐蚀金属电极板.
3. 什么是电磁流量计的正交干扰,如何消除?
   • 正交干扰: 采用交变磁场时,$\dot{B}=B_m\sin 2\pi ft$,当$\overline{v}=0$时,感生电动势测量回路所围面积$A\ne 0$,$B\perp A$,则$E$回路产生$\dot{E_t}=-k\frac{d\varphi }{dt}=-k2\pi f{B}_m\sin (2\pi ft+\frac{\pi }{2})$,$\dot{E_t}$与$\dot{E}$串联,产生串模干扰,$|\dot{E_t}|>|\dot{E}|$,由于频率相同,无法滤波消除,相位差$\frac{\pi }{2}$,故称$\dot{E_t}$为正交干扰.
   • 消除电路:
     
     调节滑动电阻$l_1$,$l_2$,使得当$\overline{v}=0$时,$\dot{E}=0$.即$l_1\cdot E_{t{\varphi }_1}+l_2\cdot E_{t{\varphi }_2}=0$,消除了正交干扰
4. 电磁流量计的特点:
   • 无任何可动部件,亦无插入管道内的部分,对流场不产生影响,几乎不存在压力损失.
   • 直管段要求前5~10D的直管段

超声波流量计

1. 超声波的发生与接收
   超声波传感器由压电材料制成

   • 逆压电效应将电振动转换成机械振动超声波,作为发射探头
   • 正压电效应将超声波转化成电信号,作接收探头

2. 超声波流量计工作原理
   用流速法,利用超声波在介质中传播的物理学现象,测出超声波通道上流体的流速,由此(估)计算截面上的平均流速进而获得流量信号

3. 超声波的测速时间差法,频率差法,多普勒法原理及局限性?为什么时间差法频率差法无法准确测速的原因?

   1. 时间差法

      • 原理
        顺流时,A发B收,所需时间$T_1=\frac{L}{c+v}$
        逆流时,B发A收,所需时间$T_2=\frac{L}{c-v}$
        时间差$\Delta T=T_1-T_2=\frac{2vL}{c^2-v^2}$,由于$c\gg v$,$\Delta T\approx \frac{2vL}{c^2}$,故而可以通过测量T测得v.
      • 局限性:
        1. 温度的变化对波速$C$的影响大,温度越高,$C$越大
        2. 激励信号和响应信号在时序上无法准确找到对应的时间点,故时间差无法确定.即由于$T_1$,$T_2$无法准确得出,故而从原理上无法准确测速

   2. 频率差法

      • 原理: 将$T_1$,$T_2$取倒数,$\Delta f=f_1-f_2=\frac{1}{T_1}-\frac{1}{T_2}=\frac{2v}{L}$得到$v=\frac{1}{2}L\cdot \Delta f$
      • 局限性: 由于$\Delta f$是由$T_1$,$T_2$得来,此法与时间差法同样无法准确测速

   3. 多普勒法:

      • 原理:
        顺流时,A发B收,接收到的超声波频率$f_{顺}$,$\lambda f_{顺}=c+v$
        逆流时,B发A收,接收到的超声波频率$f_{逆}$,$\lambda f_{逆}=c-v$
        初始时,A法B收,在B接收到A发出的超声波后采样,信号处理得到$f_{顺}$;之后AB切换工作状态,改为B发A收,A收到超声波后采样,信号处理得到$f_{逆}$;求频率差$\Delta f=f_{顺}-f_{逆}$. 得到$v=\frac{1}{2}\lambda \Delta f$.
        $v$测量的是超声波通道上的平均流速,不是截面上的平均流速.

4. 超声波流量计特点,适用流体?

   1. 无任何阻流件,压力损失小
   2. 无任何机械可动作件,可靠性高
   3. 数字式输出($\Delta f$),易于处理
   4. 所测流速是超声波通道上介质的平均流速,而非截面上的平均流速,两者间无必然联系
   5. 范围度很大,100:1 ~ 200:1
   6. 适用液体流体
   7. 流速测量不受温度,压力,粘度密度变化的影响
   8. 要求前15D,后5D的直管段
   9. 精度可达$\pm 1\%$
   10. 一般不用于高温介质(超过居里温度,压电晶体的压电效应就没了)

动压式流量测量方法及仪表

动压式流量测量仪表的理论基础: 流体流动的能量守恒方程-伯努利方程

1. 皮托管

   1. 理论基础: 流体流量的能量守恒方程
      $$流线上的流体能量=压力头P+高度头\rho gh+速度头\frac{1}{2}\rho v^2=常数$$

   2. 工作原理:
      如图,测出A点流速,以压差形式表征.将流速转化为差压,$v=\sqrt{\frac{2}{\rho }\Delta P}$
      
      输入信号: 流线上A点的流速$v_A$
      输入信号: 差压$\Delta P=P_Z-P_J$
      灵敏度: $S=\frac{\Delta Y}{\Delta X}=\frac{d\Delta P}{dv}=\rho v$

   3. 皮托管的局限性

      1. 测得的是点流速,而非平均流速
      2. 灵敏度低
      3. 开口需正对来流

2. 动压平均管

   • 工作原理: 设想可测得管内流体某一固定截面上的平均动压进而求得$v=\sqrt{\frac{2}{\rho }\Delta P}$
     
   • 优点: 设想可以得到$\overline{v}$
   • 局限性:
     1. 与皮托管相比,灵敏度并无改善
     2. 开口仍需正对来流

3. 翼形动压管的工作原理,与皮托管,阿牛巴管相比的优点和局限性

   • 工作原理:
     
     $P_A=P_1+\frac{1}{2}\rho v_1^2(1-4{\sin }^2\theta )$
     $P_B=P_1-\frac{3}{2}\rho v^2$
     $\Delta P=P_A-P_B=2\rho v_1^2$
   • 优点: 相比皮托管,阿牛巴管,其灵敏度提高3倍
   • 缺点: 流速升高,灵敏度提高,但压力损失也增大

差压流量计

1. 差压式流量测量装置的测量原理
   在流管内装入一次装置后,在其上游侧与下游侧(或咽喉部)之间前后产生一个静压力差,对于一定形状的一次装置,一定的测压位置和前后直管段情况,一定参数的流体和其它条件下,此静压力差随流量而改变,两者之间存在确定的函数关系,实现了从流量到差压的转换,可通过测差压来确定流量.

2. 标准节流装置的组成: 标准节流件,符合标准的取压装置,节流件前后直管段

3. 标准节流装置

   1. 角接取压标准孔板
   2. 法兰取压标准孔板
   3. $D$和$\frac{1}{2}D$取压标准孔板
   4. 角接取压标准喷嘴
   5. $D$和 1 2 D \frac{1}{2}D