LambertW函数的求解方法,相关性质以及绘图Matlab代码
1 Lambert W函数简述
1.1 前言
以一个具体例子作为引子,对于 2 x = x {2^x} = x 2x=x之类的超越方程,我们通常采用郎柏 W W W函数作为工具进行求解。尽管这种超越方程可以用软件进行求解,可这种基本的基于郎柏 W W W函数的求解方法还是很值得学习的。接下来,我将依次介绍这个方程的详细解答过程,郎柏 W W W函数的相关知识以及郎柏W函数相关 m a t l a b matlab matlab代码。
话不多说,上手此方程的解答过程(先说明没有实数解)。
1.2 解答过程
首先,我们需要利用 W W W函数的基本的性质(这个会在后面讲到),凑出 x e x x{e^x} xex 的形式,对应于这个方程,我们需要通过移项,得到这个式子:
2 x = x ⇒ ( − x ) ⋅ 2 − x = − 1 ⇒ ( − x ⋅ ln 2 ) ⋅ e − x ⋅ ln 2 = − ln 2 \begin{array}{l} {2^ x} = x\\ \Rightarrow \left( { - x} \right) \cdot {2^ { - x}} = - 1\\ \Rightarrow \left( { - x \cdot \ln 2} \right) \cdot {e^{ - x \cdot \ln 2}} = - \ln 2 \end{array}\\ 2x=x⇒(−x)⋅2−x=−1⇒(−x⋅ln2)⋅e−x⋅ln2=−ln2
两边分别进行郎柏 W W W 化,得到:
W [ ( − x ⋅ ln 2 ) ⋅ e − x ⋅ ln 2 ] = W ( − ln 2 ) W\left[ {\left( { - x \cdot \ln 2} \right) \cdot {e^{ - x \cdot \ln 2}}} \right] = W\left( { - \ln 2} \right)\\ W[(−x⋅ln2)⋅e−x⋅ln2]=W(−ln2)
由于 W W W 函数是 f ( x ) = x ⋅ e x f\left( x \right) = x \cdot {e^x} f(x)=x⋅ex的反函数,则这个式子可化为:
( − x ⋅ ln 2 ) = W ( − ln 2 ) ⇒ x = − W ( − ln 2 ) ln 2 \begin{array}{l} \left( { - x \cdot \ln 2} \right) = W\left( { - \ln 2} \right)\\ \Rightarrow x = - \frac{{W\left( { - \ln 2} \right)}}{{\ln 2}} \end{array}\\ (−x⋅ln2)=W(−ln2)⇒x=−ln2W(−ln2)
W W W 函数有很多分支,在这里我们取主分支 W 0 ( x ) {W_0}\left( x \right) W0(x) ,用matlab求解具体数值得:
x = 0.8247 − 1.5674 i x = 0.8247 - 1.5674i\\ x=0.8247−1.5674i
取负一分支 W − 1 ( x ) {W_{ - 1}}\left( x \right) W−1(x) 得:
x = 0.8247 + 1.5674 i x=0.8247+1.5674i x=0.8247+1.5674i
可能你会疑惑,bro,这些都是个啥?
接下来你听到的,就是保姆级郎柏 W 函数的教程,包括基本知识,拓展题和郎柏 W 函数相关matlab代码。
2 朗柏W函数的具体概念
朗柏 W W W函数是数学上的一个特殊函数,它主要用于解决以下形式的方程:
z e z = W z{e^z} = W\\ zez=W
这里, e e e是自然对数的底, z z z 是复数。给定 W W W ,我们要求解 z z z 。
而为了求解 z z z ,我们可以对其求反函数。于是,作为 f ( z ) = z e z f\left( z \right) = z{e^z} f(z)=zez 的反函数,郎柏 W W W 函数定义为 z = W ( z ) e W ( z ) z = W\left( z \right){e^{W\left( z \right)}} z=W(z)eW(z) 。(反函数的性质: y ( x ) ⋅ x ( y ) = x y\left( x \right) \cdot x\left( y \right) = x y(x)⋅x(y)=x )
为何关心这样的方程?因为它在许多数学、物理和工程问题中都有出现。特别是在解复合指数函数时,这种方程出现得很自然。
2.1 郎柏 W 函数的分支
由于 z z z 为复数,故函数 f f f 不是单映射,因此函数 W W W 是多值的。考虑该方程在某些区域有多个解,因此 W W W 函数实际上有多个分支。最常用的是主分支和负一分支。
具体而言,由于 z z z 是一个复数,为了简化,当我们把 z z z 限制为实数,且要求 W W W 是实数时,函数就只在 z ∈ ( − 1 e , + ∞ ) z \in \left( { - \frac{1}{e}, + \infty } \right) z∈(−e1,+∞)区间上有意义。这说明我们定义的分支里有意义的区域都是落在这个区间里的。
所以什么是主分支呢?
2.1.1 主分支
当我们进一步加上 W ≥ − 1 W \ge - 1 W≥−1 的限制后,就形成了一个单值函数,即 W 0 ( z ) {W_0}\left( z \right) W0(z) 。对于 z > 0 z>0 z>0 ,该函数的值始终为正。
2.1.2 负一分支
对于负一分支,定义就简单多了。在共同有意义的区间内的 w ≤ − 1 w \le - 1 w≤−1 的分支,就是负一分支。 这是主分支左侧的分支,适用于 − 1 e ≤ z < 0 - \frac{1}{e} \le z < 0 −e1≤z<0 ,在这个范围里的 x x x 值,函数的值始终为负。
2.1.3 matlab绘图
通过 m a t l a b matlab matlab画了 W 0 ( z ) {W_0}\left( z \right) W0(z) 和 W − 1 ( z ) {W_{-1}}\left( z \right) W−1(z) 的图。我们可以从图像中看到,对于主分支, W 0 ( 0 ) = 0 {W_0}\left( 0 \right) = 0 W0(0)=0 , W 0 ( − 1 e ) = − 1 {W_0}\left( { - \frac{1}{e}} \right) = - 1 W0(−e1)=−1;而对于负一分支, W W W函数从 W − 1 ( − 1 e ) = − 1 {W_{ - 1}}\left( { - \frac{1}{e}} \right) = - 1 W−1(−e1)=−1,递减为 W − 1 ( 0 − ) = ∞ {W_{ - 1}}\left( {{0^ - }} \right) = \infty W−1(0−)=∞ 。
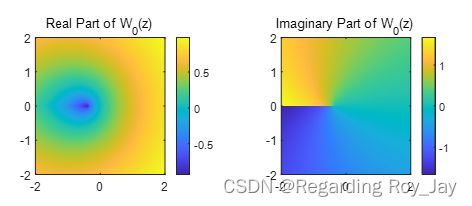
这张图是 W 0 ( z ) {W_0}\left( z \right) W0(z)在复平面上实轴与虚轴的图。

这张图是 W − 1 ( z ) {W_{-1}}\left( z \right) W−1(z)实轴与虚轴的复平面图。
这张图就是 W W W函数在 x y xy xy坐标系下的图了,可以很好地看 W 0 ( z ) {W_0}\left( z \right) W0(z)和 W − 1 ( z ) {W_{-1}}\left( z \right) W−1(z)的图像趋势和特殊值。
2.2 郎柏W函数的数理表达形式
所以, W W W 函数能用数理公式表示吗?
我们通常用以下公式表示郎柏 W W W 函数的积分形式和微分形式。
2.2.1 积分形式
W ( x ) = x π ∫ 0 π ( 1 − v cot v ) 2 + v 2 x + v csc v ⋅ e − v cot v d v , ∣ arg ( x ) < π ∣ W\left( x \right) = \frac{x}{\pi }\int_0^\pi {\frac{{{{\left( {1 - v\cot v} \right)}^2} + {v^2}}}{{x + v\csc v \cdot {e^{ - v\cot v}}}}dv,\left| {\arg \left( x \right) < \pi } \right|} \\ W(x)=πx∫0πx+vcscv⋅e−vcotv(1−vcotv)2+v2dv,∣arg(x)<π∣
W ( x ) = ∫ − ∞ − 1 e − 1 π ℑ [ d d x W ( x ) ] ln ( 1 − z x ) d x W\left( x \right) = \int_{ - \infty }^{ - \frac{1}{e}} { - \frac{1}{\pi }\Im \left[ {\frac{{\rm{d}}}{{{\rm{d}}x}}W(x)} \right]\ln \left( {1 - \frac{z}{x}} \right)dx} \\ W(x)=∫−∞−e1−π1ℑ[dxdW(x)]ln(1−xz)dx
若 x ∈ ( − 1 e , 0 ) , k = 1 , ± 2 , ± 3 , … x \in \left( { - \frac{1}{e},0} \right),k = 1, \pm 2, \pm 3, \ldots x∈(−e1,0),k=1,±2,±3,…,则:
W k ( x ) = 1 + ( ln x − 1 + 2 k π i ) e i 2 π ∫ 0 ∞ ln t − ln t + ln x + ( 2 k + 1 ) π i t − ln t + ln x + ( 2 k − 1 ) π i ⋅ d t t + 1 = 1 + ( ln x − 1 + 2 k π i ) e i 2 π ∫ 0 ∞ ln ( t − ln t + ln x ) 2 + ( 4 k 2 − 1 ) π 2 + 2 π ( t − ln t + ln x ) i ( t − ln t + ln x ) 2 + ( 2 k π − π ) 2 ⋅ d t t + 1 \begin{aligned} {W_k}\left( x \right) &= 1 + \left( {\ln x - 1 + 2k\pi i} \right){e^{\frac{i}{{2\pi }}\int_0^\infty {\ln \frac{{t - \ln t + \ln x + \left( {2k + 1} \right)\pi i}}{{t - \ln t + \ln x + \left( {2k - 1} \right)\pi i}} \cdot \frac{{dt}}{{t + 1}}} }}\\ &= 1 + \left( {\ln x - 1 + 2k\pi i} \right){e^{\frac{i}{{2\pi }}\int_0^\infty {\ln \frac{{{{\left( {t - \ln t + \ln x} \right)}^2} + \left( {4{k^2} - 1} \right){\pi ^2} + 2\pi \left( {t - \ln t + \ln x} \right)i}}{{{{\left( {t - \ln t + \ln x} \right)}^2} + {{\left( {2k\pi - \pi } \right)}^2}}} \cdot \frac{{dt}}{{t + 1}}} }} \end{aligned}\\ Wk(x)=1+(lnx−1+2kπi)e2πi∫0∞lnt−lnt+lnx+(2k−1)πit−lnt+lnx+(2k+1)πi⋅t+1dt=1+(lnx−1+2kπi)e2πi∫0∞ln(t−lnt+lnx)2+(2kπ−π)2(t−lnt+lnx)2+(4k2−1)π2+2π(t−lnt+lnx)i⋅t+1dt
通过将 W k ( x ) {W_k}\left( x \right) Wk(x)的实部和虚部展开,并用换元法化简后,得到:
W 0 ( x ) = 1 + ( ln x − 1 ) e − 1 π ∫ 0 ∞ arg ( t − ln t + ln x + π i ) d t t + 1 , x > 0 {W_0}\left( x \right) = 1 + \left( {\ln x - 1} \right){e^{ - \frac{1}{\pi }\int_0^\infty {\arg \left( {t - \ln t + \ln x + \pi i} \right)\frac{{dt}}{{t + 1}}} }},x > 0\\ W0(x)=1+(lnx−1)e−π1∫0∞arg(t−lnt+lnx+πi)t+1dt,x>0
2.2.2 微分形式
由隐函数的求导法则,(即, d x d y = 1 f ′ y , d 2 x d y 2 = d d x d y d x ⋅ d x d y = − f ′ ′ y ( f ′ y ) 3 \frac{{dx}}{{dy}} = \frac{1}{{{{f'}_y}}},\frac{{{d^2}x}}{{d{y^2}}} = \frac{{d\frac{{dx}}{{dy}}}}{{dx}} \cdot \frac{{dx}}{{dy}} = - \frac{{{{f''}_y}}}{{{{\left( {{{f'}_y}} \right)}^3}}} dydx=f′y1,dy2d2x=dxddydx⋅dydx=−(f′y)3f′′y )
郎柏 W W W 函数的微分方程为:
z [ 1 + W ( z ) ] d d z W ( z ) = W ( z ) z\left[ {1 + W\left( z \right)} \right]\frac{d}{{dz}}W\left( z \right) = W\left( z \right)\\ z[1+W(z)]dzdW(z)=W(z)
因此,
d d z W ( z ) = W ( z ) z [ 1 + W ( z ) ] , z ≠ − 1 e \frac{d}{{dz}}W\left( z \right) = \frac{{W\left( z \right)}}{{z\left[ {1 + W\left( z \right)} \right]}},z \ne - \frac{1}{e}\\ dzdW(z)=z[1+W(z)]W(z),z=−e1
而对 W W W 函数进行积分后的形式为:
∫ W ( x ) d x = x ⋅ [ W ( x ) − 1 + 1 W ( x ) ] + C \int {W\left( x \right)dx = x \cdot \left[ {W\left( x \right) - 1 + \frac{1}{{W\left( x \right)}}} \right]} + C\\ ∫W(x)dx=x⋅[W(x)−1+W(x)1]+C
在 [ 0 , 1 ] \left[ {0,1} \right] [0,1]上积分则为
∫ 0 1 W ( x ) d x = Ω + 1 Ω − 2 ≈ 0.3304 \int_0^1 {W\left( x \right)dx} = \Omega + \frac{1}{\Omega } - 2 \approx 0.3304\\ ∫01W(x)dx=Ω+Ω1−2≈0.3304
其中 Ω Ω Ω 为欧米加常数,它的值大约为 0.5671432904097838729999686622 0.5671432904097838729999686622 0.5671432904097838729999686622 ( O E I S OEIS OEIS数列 A 030178 A030178 A030178),我们可以用迭代的方法来计算 Ω Ω Ω ,即以下递推数列:
Ω n + 1 = e − Ω n {\Omega _{n + 1}} = {e^{ - \Omega n}}\\ Ωn+1=e−Ωn
其中, lim n → ∞ ∑ Ω n = Ω \mathop {\lim }\limits_{n \to \infty } \sum {{\Omega _n}} = \Omega n→∞lim∑Ωn=Ω。即,此级数的极限收敛于欧米伽常数 Ω \Omega Ω。
2.2.3 小结
相信第一眼看到 W ( z ) W\left( z \right) W(z) 的这么复杂的微分积分的表达式,尤其是它的积分性质,可能你已经 “一个字绝了” “一个字绝了” “一个字绝了”。但我们平时用它来解方程的时候用不上这些,用的都是它的性质。
2.3 郎柏W函数的性质
2.3.1 一般性质
在进行求解这种超越方程时,主要应用的性质是如下这种 ( k > 0 ) \left( {k > 0} \right) (k>0):
W ( k ln k ) = ln k W\left( {k\ln k} \right) = \ln k\\ W(klnk)=lnk
W ( − ln k k ) = − ln k W\left( { - \frac{{\ln k}}{k}} \right) = - \ln k\\ W(−klnk)=−lnk
第二个性质也是第一个的变式,因为 − ln k = ln ( 1 k ) - \ln k = \ln \left( {\frac{1}{k}} \right) −lnk=ln(k1)( p . s . p.s. p.s.一段痛苦的回忆~)
这些性质都是利用的 W ( x ) W\left( x \right) W(x) 的定义,解方程时就需要将方程看成一个一个的 W ( x e x ) = x W\left( {x{e^x}} \right) = x W(xex)=x ——因为 f ( x ) = x e x f\left( x \right) = x{e^x} f(x)=xex 的反函数就是 W ( x ) W\left( x \right) W(x) 。具体说来, W ( k ln k ) = W ( ln k ⋅ e ln k ) = ln k W\left( {k\ln k} \right) = W\left( {\ln k \cdot {e^{\ln k}}} \right) = \ln k W(klnk)=W(lnk⋅elnk)=lnk。这种变换同样也是解方程时应用的技巧。
其实,纵观一些数理知识某些难题所用的解法,大多都来自于所应用的知识点的公式推导过程的变形。
话题拉回来,上面两个基本形式的变形就是如下这些等式:
W [ − ln ( x + 1 ) x ( x + 1 ) 1 x ] = − x + 1 x ln ( x + 1 ) , x ∈ ( − 1 , 0 ) W\left[ { - \frac{{\ln \left( {x + 1} \right)}}{{x{{\left( {x + 1} \right)}^{\frac{1}{x}}}}}} \right] = - \frac{{x + 1}}{x}\ln \left( {x + 1} \right),x \in \left( { - 1,0} \right)\\ W[−x(x+1)x1ln(x+1)]=−xx+1ln(x+1),x∈(−1,0)
W ( i π ) = − i π W\left( {i\pi } \right) = - i\pi \\ W(iπ)=−iπ
W ( − i π ) = i π W\left( { - i\pi } \right) = i\pi \\ W(−iπ)=iπ
上面的式子巧妙地应用了欧拉公式,即
e i π = cos π + i sin π = − 1 {e^{i\pi }} = \cos \pi + i\sin \pi = - 1\\ eiπ=cosπ+isinπ=−1
故,
W ( − i π ) = W ( e i π ⋅ i π ) = i π W\left( { - i\pi } \right) = W\left( {{e^{i\pi }} \cdot i\pi } \right) = i\pi \\ W(−iπ)=W(eiπ⋅iπ)=iπ
v i s e v e r s a vise \quad versa viseversa~
于是便诞生了一些相关的特殊值,如
W ( − ln 2 2 ) = − ln 2 W\left( { - \frac{{\ln 2}}{2}} \right) = - \ln 2\\ W(−2ln2)=−ln2
W ( − 1 e ) = − 1 W\left( { - \frac{1}{e}} \right) = - 1\\ W(−e1)=−1
W ( e ) = W ( e 1 ⋅ 1 ) = 1 W\left( e \right) = W\left( {{e^1} \cdot 1} \right) = 1\\ W(e)=W(e1⋅1)=1
W ( e e + 1 ) = W ( e e ⋅ e ) = e W\left( {{e^{e + 1}}} \right) = W\left( {{e^e} \cdot e} \right) = e\\ W(ee+1)=W(ee⋅e)=e
W ( − π 2 ) = π 2 i W\left( { - \frac{\pi }{2}} \right) = \frac{\pi }{2}i\\ W(−2π)=2πi
(注:这个公式也用到了欧拉公式,和上面的推导一样)
它还有其他一些有趣的性质,比如:
z z z z z . . . = lim n → ∞ ( z ↑ ↑ n ) = − W ( − ln z ) ln z {z^{{z^{{z^{{z^{{z{...} }}}}}}}}} = \mathop {\lim }\limits_{n \to \infty } \left( {z \uparrow \uparrow n} \right) = - \frac{{W\left( { - \ln z} \right)}}{{\ln z}}\\ zzzzz...=n→∞lim(z↑↑n)=−lnzW(−lnz)
其中 ↑ ↑ \uparrow \uparrow ↑↑ 是高德纳箭号表示法。(是否和开头的例子的结果类似?)
如果 z > 0 z>0 z>0 ,还有 ln W ( z ) = ln z − W ( z ) \ln W\left( z \right) = \ln z - W\left( z \right) lnW(z)=lnz−W(z) 。
2.3.2 泰勒级数
既然它是一个函数,那它会不会有泰勒级数呢?
还真有, W 0 {W_0} W0 在 x = 0 x=0 x=0 展开的泰勒级数为:
W 0 ( x ) = ∑ n = 1 ∞ ( − 1 ) n − 1 n n − 1 n ! x n = x − x 2 + 3 2 x 3 − 8 3 x 4 + 125 24 x 5 − ⋯ {W_0}\left( x \right) = \sum\limits_{n = 1}^\infty {{{\left( { - 1} \right)}^{n - 1}}\frac{{{n^{n - 1}}}}{{n!}}} {x^n} = x - {x^2} + \frac{3}{2}{x^3} - \frac{8}{3}{x^4} + \frac{{125}}{{24}}{x^5} - \cdots \\ W0(x)=n=1∑∞(−1)n−1n!nn−1xn=x−x2+23x3−38x4+24125x5−⋯
收敛半径为 1 e \frac{1}{e} e1。
那既然有收敛半径,总得有收敛区间吧?
有同学就想当然得想到收敛区间可能是 x ∈ ( − 1 e , 1 e ) x \in \left( { - \frac{1}{e},\frac{1}{e}} \right) x∈(−e1,e1) ,
但是 ∣ x ∣ = 1 e \left| x \right| = \frac{1}{e} ∣x∣=e1 时的情况需要讨论。
就拿 x = − 1 e x = - \frac{1}{e} x=−e1 时来说,此时,
u n = ( − 1 ) 2 n − 1 n n − 1 n ! ⋅ ( 1 e ) n = − n n − 1 n ! ⋅ ( 1 e ) n \begin{aligned} {u_n} &= {\left( { - 1} \right)^{2n - 1}}\frac{{{n^{n - 1}}}}{{n!}} \cdot {\left( {\frac{1}{e}} \right)^n}\\ &= - \frac{{{n^{n - 1}}}}{{n!}} \cdot {\left( {\frac{1}{e}} \right)^n} \end{aligned}\\ un=(−1)2n−1n!nn−1⋅(e1)n=−n!nn−1⋅(e1)n
我们可以对 u n {u_n} un 加绝对值(注:后面发现不用这样做,这里当是复习一下考研数学吧),由绝对值不等式,得 u n ≤ ∣ u n ∣ {u_n} \le \left| {{u_n}} \right| un≤∣un∣,
故,由比较审敛法得,当级数 { ∣ u n ∣ } \left\{ {\left| {{u_n}} \right|} \right\} {∣un∣} 收敛时, { u n } \left\{ {{u_n}} \right\} {un}必收敛(大的收敛,小的必收敛;小的发散,大的必发散)
所以接下来,将用比值审敛法讨论 { ∣ u n ∣ } \left\{ {\left| {{u_n}} \right|} \right\} {∣un∣}的收敛情况。
这里先不取极限,原因一会儿就知道了。
于是:
u n + 1 u n = ( n + 1 ) n n ! ( n + 1 ) ! n n − 1 e n e n + 1 = 1 e ⋅ ( n + 1 ) n − 1 ( n ) n − 1 = ( 1 + 1 n ) n − 1 e \begin{aligned} \frac{{{u_{n + 1}}}}{{{u_n}}} &= \frac{{{{\left( {n + 1} \right)}^n}n!}}{{\left( {n + 1} \right)!{n^{n - 1}}}}\frac{{{e^n}}}{{{e^{n + 1}}}}\\ &= \frac{1}{e} \cdot \frac{{{{\left( {n + 1} \right)}^{n - 1}}}}{{{{\left( n \right)}^{n - 1}}}}\\ &= \frac{{{{\left( {1 + \frac{1}{n}} \right)}^{n - 1}}}}{e} \end{aligned}\\ unun+1=(n+1)!nn−1(n+1)nn!en+1en=e1⋅(n)n−1(n+1)n−1=e(1+n1)n−1
所以,你就可以看到,如果对其求极限,会发现极限为 1 1 1,根据比值审敛法,当极限为 1 1 1时,审敛法就失效了。
在审敛法失效的情况下,考研张宇的方法就显得十分绝妙了。
回归定义,令 f ( x ) = ( 1 + 1 x ) x − 1 f\left( x \right) = {\left( {1 + \frac{1}{x}} \right)^{x - 1}} f(x)=(1+x1)x−1 ,我们对其进行求导,(当然是两边取对数求导啦,你也可以变成 e x p exp exp函数,由于这种求导是基本功,所以就不展示了)发现在 x > 0 x>0 x>0 时它是从 0 0 0开始增加,且单调递增的,然后我们对它取极限,发现它是趋向于 e e e 的。就是说,
( 1 + 1 n ) n − 1 < e {\left( {1 + \frac{1}{n}} \right)^{n - 1}} < e\\ (1+n1)n−1<e
则:
( 1 + 1 n ) n − 1 e < 1 ⇒ u n + 1 u n < 1 \begin{array}{l} \frac{{{{\left( {1 + \frac{1}{n}} \right)}^{n - 1}}}}{e} < 1\\ \Rightarrow \frac{{{u_{n + 1}}}}{{{u_n}}} < 1 \end{array}\\ e(1+n1)n−1<1⇒unun+1<1
所以 { u n } \left\{ {{u_n}} \right\} {un} 是收敛的,故 x x x可以取到 − 1 e - \frac{1}{e} −e1 。
当 x = 1 e x = \frac{1}{e} x=e1 时, { u n } \left\{ {{u_n}} \right\} {un}是交错级数。由于前面证明了 x = − 1 e x = - \frac{1}{e} x=−e1 ,即 { u n } \left\{ {{u_n}} \right\} {un}没有 ( − 1 ) n − 1 {\left( { - 1} \right)^{n - 1}} (−1)n−1时,(就是类似于加了绝对值的情况)是收敛的,说明此交错级数就是绝对收敛的。所以 x x x 同样可以取到 − 1 e - \frac{1}{e} −e1 。
因此, W 0 ( x ) {W_0}\left( x \right) W0(x) 的收敛区间为 x ∈ [ − 1 e , 1 e ] x \in \left[ { - \frac{1}{e},\frac{1}{e}} \right] x∈[−e1,e1] 。
2.3.3 其余性质
最后再补充 W W W 函数的一些性质收个尾
加法定理:
W ( x ) + W ( y ) = W [ x y W ( x ) + x y W ( y ) ] , x > 0 , y > 0 W\left( x \right) + W\left( y \right) = W\left[ {\frac{{xy}}{{W\left( x \right)}} + \frac{{xy}}{{W\left( y \right)}}} \right],x > 0,y > 0\\ W(x)+W(y)=W[W(x)xy+W(y)xy],x>0,y>0
3 应用与实操
在学习了以上知识后,来看这道题。
[ 例题 ] [例题] [例题]
用数理方法解出以下超越方程:
2 x + x − 3 = 0 {2^x} + x - 3 = 0\\ 2x+x−3=0
对于这道题,主要思路就是要利用 W W W 函数的性质,即 W ( x e x ) = x W\left( {x{e^x}} \right) = x W(xex)=x 来进行方程的求解。
首先,我们得移项:
2 x = − ( x − 3 ) {2^x} = - \left( {x - 3} \right)\\ 2x=−(x−3)
然后利用幂的性质,两边乘以 2 − 3 = 8 {2^{ - 3}}=8 2−3=8 ,使方程两边都凑出 ( x − 3 ) \left( {x - 3} \right) (x−3) 项,即
2 x − 3 = − x − 3 8 8 = − ( x − 3 ) ⋅ 2 − ( x − 3 ) = − ( x − 3 ) ⋅ e − ( x − 3 ) ⋅ ln 2 8 ln 2 = [ − ( x − 3 ) ⋅ ln 2 ] ⋅ e [ − ( x − 3 ) ⋅ ln 2 ] \begin{aligned} {2^{x - 3}} &= - \frac{{x - 3}}{8}\\ 8 &= - \left( {x - 3} \right) \cdot {2^{ - \left( {x - 3} \right)}}\\ & = - \left( {x - 3} \right) \cdot {e^{ - \left( {x - 3} \right) \cdot \ln 2}}\\ 8\ln 2 &= \left[ { - \left( {x - 3} \right) \cdot \ln 2} \right] \cdot {e^{\left[ { - \left( {x - 3} \right) \cdot \ln 2} \right]}} \end{aligned}\\ 2x−388ln2=−8x−3=−(x−3)⋅2−(x−3)=−(x−3)⋅e−(x−3)⋅ln2=[−(x−3)⋅ln2]⋅e[−(x−3)⋅ln2]
然后,将等式两边 W W W 函数一下,得:
( x − 3 ) ln 2 = W ( 8 ln 2 ) \left( {x - 3} \right)\ln 2 = W\left( {8\ln 2} \right)\\ (x−3)ln2=W(8ln2)
这时候,如果取主分支 W 0 ( z ) {W_0}\left( z \right) W0(z),精彩的事就发生了:
8 ln 2 8\ln 2 8ln2 可以写成 2 2 ln 2 2 {2^2}\ln {2^2} 22ln22, 就可以消掉 W W W 函数的形式,故:
− ( x − 3 ) ln 2 = ln 4 3 − x = ln 4 ln 2 x = 1 \begin{aligned} - \left( {x - 3} \right)\ln 2 &= \ln 4\\ 3 - x &= \frac{{\ln 4}}{{\ln 2}}\\ x &= 1 \end{aligned}\\ −(x−3)ln23−xx=ln4=ln2ln4=1
可能有人会觉得这种方法多此一举,但这只是个举例,为了方便巩固以上所学知识及其附加的计算能力,但不能因为这个例子局限了 W W W 函数的神通广大。( b u s h i bushi bushi)
4 代码
有同学说,光听你说这 W W W 函数那 W W W 函数,我想要自己画个 W W W 函数的图像方便自己研究该怎么办。。。
不要慌,这就给各位同学呈上基于 W W W 函数的 x O y xOy xOy 坐标和复数域的图像的 m a t l a b matlab matlab代码。
废话几句,首先你得有 m a t l a b matlab matlab软件,然后,你的 m a t l a b matlab matlab得有 L a m b e r t w Lambertw Lambertw工具箱。
如果没有预先安装,你可以从MATLAB的文件交换中心下载 Lambert W函数的工具包。
代码来咯~:
Lambertw_main.m
clc,clear
% 绘制实数轴上的Lambert W函数
x_real = linspace(-0.3517,2,1000); % -1/e约等于-0.3517是Lambert W函数的定义域下界
y_real_0 = lambertw(0,x_real); % 主分支
y_real_1 = lambertw(-1,x_real); % -1分支,仅在[-1/e, 0]有定义
figure;
plot(x_real,y_real_0,'color','#D95319','LineWidth',1.5);
hold on;
plot(x_real, y_real_1,'color', '#0072BD','LineWidth',1.5);
legend('Main branch (W_0)','Secondary branch (W_{-1})');
xlabel('$x$','interpreter','latex','FontWeight','bold');
ylabel('$W\left(x\right)$','interpreter','latex','FontWeight','bold');
title('Lambert W function on real axis');
grid on;
% 绘制Lambert W函数在复平面上的行为
[x, y] = meshgrid(linspace(-2,2,400),linspace(-2,2,400));
z = x + 1i*y;
w0 = lambertw(0, z);
w1 = lambertw(-1,z);
figure;
subplot(2,2,1);
imagesc(linspace(-2,2,400),linspace(-2,2,400),real(w0));
axis xy; colorbar;
title('Real Part of W_0(z)');
subplot(2,2,2);
imagesc(linspace(-2,2,400), linspace(-2,2,400),imag(w0));
axis xy; colorbar;
title('Imaginary Part of W_0(z)');
subplot(2,2,3);
imagesc(linspace(-2,2,400),linspace(-2,2,400),real(w1));
axis xy; colorbar;
title('Real Part of W_{-1}(z)');
subplot(2,2,4);
imagesc(linspace(-2,2,400),linspace(-2,2,400),imag(w1));
axis xy; colorbar;
title('Imaginary Part of W_{-1}(z)');
对于关键代码已进行了注释,一条龙服务。[傲娇.jpg]
你说 d i s p l a y display display的结果是啥?前面的图就是的。
尾声
朗柏 W W W函数在许多数学和物理问题中都有应用。例如:
- 解决某些微分方程。
- 在复杂网络的理论中描述网络的增长。
- 在统计物理中描述某些系统的行为。
- 在经济学中,描述某些增长模型。
总的来说,朗柏 W W W函数是解决具有复合指数形式方程的关键工具。
尾声过于简短了,但祝学有所成,功不唐捐!
参考文献:
-
^T.C. Scott and R.B. Mann, General Relativity and Quantum
Mechanics: Towards a Generalization of the Lambert W Function, AAECC
(Applicable Algebra in Engineering, Communication and Computing),
vol. 17, no. 1,(April 2006),pp.41-47. -
^ P.S. Farrugia, R.B. Mann, and T.C. Scott, N-body Gravity and the Schrodinger Equation, Class. Quantum Grav. vol. 24, (2007),
pp.4647-4659. -
^ Aude Maignan, T.C. Scott, “Fleshing out the Generalized Lambert W Function”, SIGSAM, vol. 50, no.2, (June 2016),pp. 45-60.
-
^ Michon, G. P. “Final Answers: Numerical Constants.”
http://www.numericana.com/answer/constants.htm#omega. -
.^ Moll, V. H. “Some Questions in the Evaluation of Definite
Integrals.” MAA Short Course, San Antonio, TX. Jan. 2006.https://web.archive.org/web/20080402045620/http://crd.lbl.gov/~dhbaiey/expmath/maa-course/Moll-MAA.pdf. -
^张宇高等数学18讲/张宇主编. -北京:北京理工大学出版社,2022.1(2023.1重印). ISBN
978-7-5763-0851-8.
