题目大意:有n个点(x,y<=10^9,n<=1500),求出这n个点组成的三角形是直角三角形的方案数。
【做法1】
暴力枚举直角三角形的三个点,再用勾股定理判断是否是直角。时间复杂度O(n^3)。
【做法2】
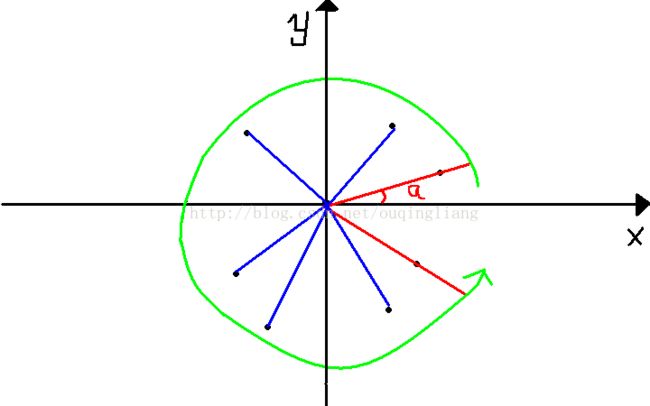
假设原点也是点,则可以按照x轴正半轴旋转到每个点所需的角度排序,然后用单调队列扫描一遍。
如下图所示:
那么我们可以枚举每个点A作为直角三角形斜边对应的点,也就是直角点,那么其他点B的坐标就要变成——(B.x-A.x,B.y-A.y),然后按上面的方法算就可以了。
则时间复杂度O(n^2logn),编程复杂度高,容易错。
【做法3】
考虑到直角是90度,那么,将直角边上的一点旋转90度,便与另一条线重合。于是我们可以把每个点都记住它原始的象限,再每次旋转90度,旋转到第一象限内。然后按照其斜率排序,找出其斜率相同的点,则这些点都在同一直线上。统计每个象限内的点的个数,又因为1,2象限,2,3象限,3,4象限和4,1象限是相邻的。根据乘法原理和加法原理,将每个象限内的点的个数按上面的方法计算即可。具体看程序:
#include
#include
#include
#include
#include
using namespace std;
#define Maxn 1510
typedef long long LL;
struct Point{
int x,y;
int p;
double k;
void turn(){ x=-x; swap(x,y); }//将点“逆”时针旋转90度
void calc_k()//计算斜率
{
if(x==0) k = 1000000001;
else k = (0.0+y)/(0.0+x);
}
};
bool cmp(Point x,Point y){return x.ky) return 0;
if(y>x) return 0;
return 1;
}
LL f[10],ans;
Point a[Maxn],b[Maxn];
int n;
int main()
{
scanf("%d",&n);
int x,y;
for(int i=1;i<=n;i++) scanf("%d%d",&a[i].x,&a[i].y);
for(int t=1;t<=n;t++)//枚举直角点,以这点建立平面直角坐标系
{
swap(a[n],a[t]);//则a[n]为直角点
memset(b,0,sizeof(b));
for(int i=1;i=0 && y<0)
{
b[i].turn(); b[i].turn(); b[i].turn();
b[i].p = 4;
}
else if(x<0 && y<=0)
{
b[i].turn(); b[i].turn();
b[i].p = 3;
}
else if(x<=0 && y>0)
{
b[i].turn();
b[i].p = 2;
}
else b[i].p = 1;
b[i].calc_k();
}
sort(b+1,b+n,cmp);//排序
int i,j;
for(i=1;i