数据结构 树的直径

学习的最大理由是想摆脱平庸，早一天就多一份人生的精彩；迟一天就多一天平庸的困扰。

学习日记

目录

学习日记

一、定义

二、两次DFS

定理：

反证法证明：

1、若y在d(t,s)上

 2、若y不在d(s,t)上，且d(y,z)与d(s.t)存在重合路径:

3、 若y不在d(s,t)上，且d(y,z)与d(s,t)不存在重合路径：​编辑

三、树形DP

状态表示 

---

一、定义

        树的直径，又称树的最长链。我们将一棵树 T = {V, E} 的直径定义为max(u,v), 也就是说，树中所有最短路径距离的最大值即为树的直径。

        显然，一棵树可以有多条直径，他们的长度相等。 可以用两次 DFS 或者树形 DP 的方法在

O(n) 时间求出树的直径。

二、两次DFS

        首先从任意节点x开始进行第一次 DFS，到达距离其最远的节点，记为y，然后再从y开始做第二次 DFS，到达距离y最远的节点，记为，则即d(y,z)为树的直径。 显然，如果第一次 DFS 到达的节点y是直径的一端，那么第二次 DFS 到达的节点 一定是直径的一端。我 们只需证明在任意情况下， 必为直径的一端。

定理：

在一棵树上，从任意节点开始进行一次 DFS，到达的距离其最远的节点必为直径的一端。

反证法证明：

        记出发点记出发节点为y。设真实的直径是d(s,t)，而从y进行的第一次 DFS 到达的距离其 最远的节点z不为t或x。共分三种情况：

1、若y在d(t,s)上

有d(y,z)>d(s,t)，则d(x,z)>d(x,t)，得d(s,z)>d(s,t),与 d(s,t) 为树的直径矛盾。

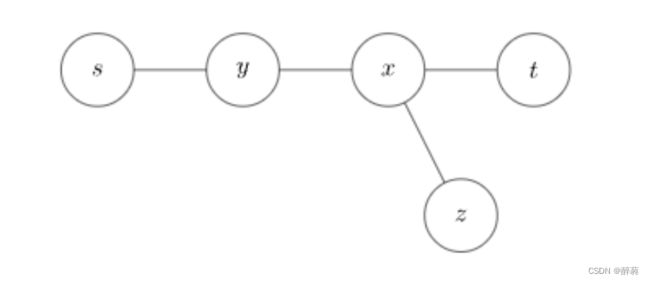
 2、若y不在d(s,t)上，且d(y,z)与d(s.t)存在重合路径:

 有d(y,z)>d(s,t)，则d(x,z)>d(x,t)，得d(s,z)>d(s,t),与d(s,t)为树的直径矛盾。

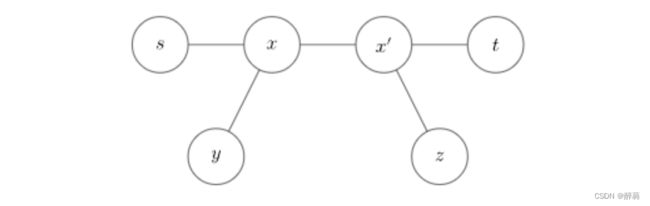
3、 若y不在d(s,t)上，且d(y,z)与d(s,t)不存在重合路径：

有d(y,z)>d(s,t)，则d(x',z)>d(x',t)，d(x,z)>d(x,t),得d(s,z)>d(s,t),与d(s,t)为树的直径矛盾。

        综上，三种情况下假设均会产生矛盾，故原定理得证。上述证明过程建立在所有路径均不为负的前提下。如树上存在负权边，则上述证明不成立。故如果存在负权边，则无法使用两次 DFS 的方式求解直径。

int maxdis,maxu; 
void dfs(int u,int fa,int dis) 
{ 
    if(maxdis < dis) maxdis = dis , maxu = u; 
    for(int i = h[u] ; ~i ; i = ne[i]) 
    { 
        int j = e[i]; 
        if(j == fa) continue;
        dfs(j,u,dis+w[i]); 
    } 
}
dfs(1,-1,0); dfs(maxu,-1,0);

三、树形DP

        记录当1为树的根时，每个节点作为子树的根向下，所能延伸的最远距离d1，和次远距离d2 ，那么直径就是所有d1+d2的最大值。树形 DP 可以在存在负权边的情况下求解出树的直径。

状态表示 

f1[i]表示以i为根的子树中，i到叶子结点距离的最大值。

f2[i]表示以i为根的子树中，i到叶子结点距离的次大值。

int f1[N],f2[N]; 
int ans;
void dfs(int u,int fa) 
{ 
    f1[u] = f2[u] = 0;
    for(int i = h[u] ; ~i ; i = ne[i]) 
    { 
        int j = e[i];
        if(j == fa) continue;
        dfs(j,u); if(f1[j]+w[i] > f1[u]) f2[u] = f1[u] , f1[u] = f1[j]+w[i]; 
        else if(f1[j] + w[i] > f2[u]) f2[u] = f1[j] + w[i]; 
    }
    ans = max(ans,f1[u]+f2[u]); 
}
dfs(1,-1);