第四章 递归、回溯与分治

一、递归（& 循环）

（1）含义
当需要重复地多次计算相同的问题，通常可以采用递归或循环。递归是在一个函数内部调用这个函数自身。
递归的本质是把一个问题分解成两个或多个小问题。（注：当多个小问题存在相互重叠的部分，就存在重复的计算）
（2）基本格式
递归一定包括两部分：（1）递归关系（2）递归出口
递归代码先写递归出口，再写递归关系。
（3）适用题型

• 递归调用的本质便是入、出栈的过程。栈中每个元素存储一种现场状态。（可以通过画系统栈分析递归数据的变化）
• 可利用高等数学中的递归函数求解，可参考如下模板：
  递归关系：f(n)与f(n-1)（f(n-2)、f(n-3)…）间的关系
  递归出口：f(0)的取值（初始值）
  等号：return
• 任何循环都能写成递归形式，但是递归不一定能用循环表示

（4）基本案例
例1：求数组最大值arr[]={7,4,8,6,3,2,9,11}
递归关系：max(arr,n)=max(arr,n-1)>arr[n]?max(arr,n-1):arr[n];
递归出口：max(arr,0)=arr[0];

int max(int[] arr,int n){
  if(n==0){
    return arr[0];
}else{
    return max(arr,n-1)>arr[n]?max(arr,n-1):arr[n];
}
}

例2：将head指针指向的节点的数据域val，push到vec中

void add_to_vector(ListNode *head,vector<int> &vec){
	if(!head)return;//如果head为空则结束递归
	vec.push_back(head.val);//将当前遍历的节点值push进入vec
	add_to_vector(head.next,vec);//继续递归后续链表
}

剑指Offer

例1：Fibonacci数列

题目描述
大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项（从0开始，第0项为0）。n<=39
解题思路
（1）递归关系

f(n)=f(n-1)+f(n-2)

（2）递归出口

f(1)=1
f(2)=1

程序代码

	public int Fibonacci(int n) {
		//题目条件
		if(n==0)return 0;
		//递归出口
		if(n==1)return 1;
		else if(n==2)return 1;
		//递归关系
		else return Fibonacci(n-1)+Fibonacci(n-2);
    }

例2：跳台阶

题目描述
一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法（先后次序不同算不同的结果）。
解题思路
（1）递归关系
青蛙跳n级台阶时，要么是从n-2级台阶跳，要么是从n-1级台阶跳，因此：
跳n级台阶的跳法 = 跳n-1级台阶的跳法 + 跳n-2级台阶的跳法

f(n) = f(n-1)+f(n-2)

（2）递归出口
由递归关系可以看出，递归出口有2个，分析：
青蛙跳1级台阶有1种跳法，跳2级台阶有2种跳法（1+1、2）

f(1)=1
f(2)=2

程序代码

    public int JumpFloor(int target) {
    		//实际情况：跳0级台阶，0种跳法
    		if(target == 0)return 0;
    	
    		//递归出口:跳1级台阶只有1种跳法，2级台阶时有2种跳法
    		if(target == 1)return 1;
    		else if(target == 2)return 2;
    		//递归关系:跳n级台阶时有f(n-1)+f(n-2)种跳法
    		else return JumpFloor(target-1)+JumpFloor(target-2);
    }

例3：变态跳台阶

题目描述
一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
解题思路
因为青蛙跳n级台阶时，可以从第n-1、n-2、n-3……1级台阶开始跳，再加上1（表示跳n级）。
可以列出递归函数式

f(n) = f(n-1) + f(n-2) + f(n-3) + ... +f(1) + 1
f(n-1) = f(n-2) + f(n-3) + f(n-4) + ... + f(1) + 1
...
f(1) = 1

利用高等数学的递归关系进行化简

1. f(n) = f(n-1) + f(n-2) + f(n-3) + ... +f(1) + 1
2. f(n) = 2*f(n-2) + 2*f(n-3) + ... +2*f(1) + 2
3. f(n) = 4*f(n-3) + ... +4*f(1) + 4
...
4. f(n) = 2^(n-2)*f(n-(n-1)) + 2^(n-2)
5. f(n) = 2^(n-1)

程序代码

    public int JumpFloorII(int target) {
        //实际情况：跳0级台阶，0种跳法
    		if(target == 0)return 0;
    		//通过高等数学中的递归计算，可以得到递归关系表达式f(n) = 2^(n-2)f(1) + 2^(n-2),f(1)=1,
    		//得出最终表达式：f(n) = 2^(n-1)
    		//Java的幂指数运算：Math.pow(double a,double b)，返回的结果是a的b次方。
    		return (int)Math.pow(2,target-1);
    }

例4：矩形覆盖

题目描述
我们可以用2 * 1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2 * 1的小矩形无重叠地覆盖一个2 * n的大矩形，总共有多少种方法？
解题思路

1. target <= 0 大矩形为<= 2 * 0,直接return 1；
2. target = 1大矩形为2 * 1，只有一种摆放方法，return1；
3. target = 2 大矩形为2 * 2，有两种摆放方法，return2；
4. target = n 分为两步考虑：

第一次摆放一块2 * 1的小矩阵，则摆放方法总共为f(target - 1)

√
√

第一次摆放一块1 * 2的小矩阵，则摆放方法总共为f(target-2)
因为，摆放了一块1 * 2的小矩阵（用√√表示），对应下方的1 * 2（用××表示）摆放方法就确定了，所以为f(targte-2)

√	√
×	×

程序代码

    public int RectCover(int target) {
    		//实际情况：矩形宽度为0，则没有覆盖方法
    		if(target == 0)return 0;
    		
    		//初始摆放有2种，若第一次竖放，则有f(n-1)种放法，如第一次横放，则第二次必须横放，共有f(n-2)种放法
    		if(target == 1)return 1;
    		else if(target == 2)return 2;
    		else return RectCover(target-1)+RectCover(target-2);
    }

二、回溯法

（1）含义
回溯法（"回溯"字面意思为回到溯源/根部）实际上是一个类似枚举（包含"剪枝"功能的穷举）的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当探索到某一步时，发现原先选择达不到目标，就退回一步重新选择，尝试别的路径，这种走不通就退回再走的技术称为回溯法。回溯法可理解为使用了递归思想的一种算法。
回溯法常用于解决走路径问题（所走路径是否满足要求）如走迷宫等。

回溯法是一个既带有系统性又带有跳跃性的的搜索算法。它在包含问题的所有解的解空间树中，按照深度优先的策略，从根结点出发搜索解空间树。算法搜索至解空间树的任一结点时，总是先判断该结点是否肯定不包含问题的解。如果肯定不包含，则跳过对以该结点为根的子树的系统搜索，逐层向其祖先结点回溯。否则，进入该子树，继续按深度优先的策略进行搜索。回溯法在用来求问题的所有解时，要回溯到根，且根结点的所有子树都已被搜索遍才结束。而回溯法在用来求问题的任一解时，只要搜索到问题的一个解就可以结束。这种以深度优先的方式系统地搜索问题的解的算法称为回溯法，它适用于解一些组合数较大的问题。
也可理解成一系列入栈操作，再进行一系列出栈操作直到栈为空，再进行一系列入栈、出栈……且出栈后要保证当前元素的状态一致。

（2）基本格式

List<> answer;//存放一个解
List<List<>> result;//返回值，存放所有解的结集

void backtrack(int i,int n,List<> answer,other parameters)
{
//i代表解空间的第i个位置，往往从0开始，而n则代表解空间的大小，一次递归表示对解空间第i个位置进行处理
  if( i == n)
{
 //处理解空间第n个位置，表示处理完解空间所有位置，为一个解。将解存入结果集。
result.add(new ArrayList(answer));
return;
}
//搜索解空间第i个位置上的所有解
for(next ans in position i of solution space)
{
//求解空间第i个位置上的下一个解
  doSomething(answer,i);//修改解的位置i
  backtrack(i+1,n,other parameters);//递归对解空间i+1位置进行处理
  RevertSomething(answer,i);//恢复解的位置i
}
}

根据下图理解递归中系统栈的变化：

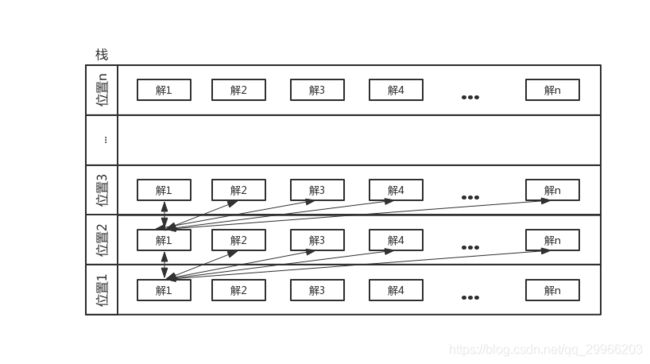
（3）理解
回溯法是一种系统搜索问题解空间的方法。为了实现回溯，需要给问题定义一个解空间。它是一种在解空间进行搜索的算法。因此，关键在于
1、解空间：解空间为形如数组的一个向量[a1,a2,…,an]。这个向量的每个元素都是问题的部分解。只有数组中每一个元素都填满（得到全部解）时，才表明问题得到了解答。
2、搜索：分别对向量中n个位置求解

for(求a1位置上的解)
   for(求a2位置上的解)
      for(求a3位置上的解)
       ......
       ......
       for(求an位置上的解)

解决回溯问题的步骤：

1. 定义问题的解空间，使得能用回溯法方便地搜索整个解空间（难点）
2. 利用深度优先的方式搜索解空间，并且在搜索过程中用剪枝函数避免无效的搜索。
   每一次的backtrack(i,n,other)调用,代表求解空间第i个位置上的解，当i=n时，代表解空间上的所有位置的解都已经求出

（4）基本案例
例1：求全排列（leetCode46）
给定一个没有重复数字的序列，返回其所有可能的全排列。
算法思路：
求一个数组的全排列，就是把这个数组中的每个位置的元素分别放在数组头部,然后求剩余元素的全排列.
递归边界是剩余元素数量为1，也就是说当数组中只剩一个元素的时候，它的全排列就是它本身。

    // 46.全排列
    //给定一个没有重复数字的序列，返回其所有可能的全排列。
    // 理解全排列：找由根出发的所有路径
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();//存储全排列的所有结果
        List<Integer> answer = new ArrayList<Integer>();	// 存储全排列一个结果
		int[] visit = new int[nums.length];	// 访问数组
		for(int i=0;i<nums.length;i++) {
			visit[i] = 0;
		}
        
		generatePermute(nums,visit,0,nums.length,answer,result);
        
        return result;
    }
    
    void generatePermute(int[] nums,int[] visit,int i,int size,List<Integer> answer,List<List<Integer>> result) {
		// 全排列集合中放置第 i 个位置元素
    		answer = new ArrayList<>(answer);
    		if(i==size) {
    			result.add(answer);//深度复制，为全排列的一个结果，存储一个对象而非引用（否则所有结果都指向同一地址，结果相同）
    			return;
    		}
    		// 遍历所有元素，若该元素未加入当前路径，则加入，并对下一个位置放置元素
    		// 回溯思想：结束该位置所有路径访问时，弹出元素，并恢复加入元素前状态（remove + visit[j]=0）
    		for(int j=0;j<size;j++)
    			if(visit[j] == 0) {
    				answer.add(nums[j]);
    				visit[j] = 1;
    	    			generatePermute(nums,visit,i+1,size,answer,result);
    	    			answer.remove(answer.size()-1);
    	    			visit[j] = 0;
    			}
    }

leetcode

例1：求子集1（原数组不包含重复元素）

题目描述
给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。
说明：解集不能包含重复的子集。
解题思路
利用回溯法生成子集，即对于每个元素，都有试探放入或不放入集合的两个选择：
选择放入该元素，递归的进行后续元素的选择，完成放入该元素后续所有元素的试探；
之后将该元素拿出，即再进行一次不放入该元素，递归的进行后续元素的选择，完成不放入该元素后续所有元素的试探。（这里"拿出"的思想即回溯法）
解空间：解空间nums第i个位置为：是否放入第i个元素的子集。
例如：元素数组：nums={1,2,3,4…}，子集生成数组item=[]
对于元素1，选择放入item=[1]，继续递归处理后续[2,3,4,5]，子集item=[1…]
选择不放入item=[]，继续递归处理后续[2,3,4,5],子集item=[…]
程序代码

	public List<List<Integer>> subsets2(int[] nums) {
		
		List<List<Integer>> result = new ArrayList<>();//存储各个子集的结果数组
		//集合化
		List<Integer> numsList = new ArrayList<Integer>(nums.length);
		for(int i=0;i<nums.length;i++)numsList.add(nums[i]);
		//表示一个子集
		List<Integer> subList = new ArrayList<Integer>();
		result.add(subList);//先加入空集
		
		generateSubsets(result,subList,numsList,0);
		
		return result;
	}
	
	public void generateSubsets(List<List<Integer>>result,List<Integer> subList,List<Integer> numsList,int idx) {
		//求nums的子集，idx表示对放入和不放入numsList[idx]的子集分别进行讨论
		if(idx == numsList.size())return;
		
		for(int i=idx;i<numsList.size();i++) {
			subList.add(numsList.get(i));//子集放入numsList.get(idx)元素
			result.add(new ArrayList<>(subList));//假如结果集
			generateSubsets(result,subList,numsList,i+1);//对后续元素继续处理
			subList.remove(subList.size()-1);//子集拿出numsList.get(idx)元素
		}
	}

例2：求子集2（原数组包含重复元素）

题目描述
给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。
说明：解集不能包含重复的子集。
解题思路
解法与【求子集1】类似。解空间为一次递归表示放入|不放入第idx元素时的子集序列。先放入idx元素，表示包含idx元素的子集情况，再对后续元素处理；再拿出idx元素，表示不包含idx元素的子集情况，再对后续元素处理。
因为原数组包含重复元素，所以需要防止重复：不同位置，相同元素组成的集合为同一子集，因为集合中元素是无序的。解决方案是先对原nums进行排序，再使用set去重。
程序代码

    public List<List<Integer>> subsetsWithDup(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();//结果数组，存储所有的子集序列
        List<Integer> subset = new ArrayList<>();//子集，为某个子集数组

        //防止重复：不同位置，相同元素组成的集合为同一子集。因为集合中的元素是无序的。
        //解决方法：先对原nums数组排序，再使用set去重
        Arrays.sort(nums);
        List<Integer> numsList = new ArrayList<>();//集合化
        for(int i=0;i<nums.length;i++)
        		numsList.add(nums[i]);
     
        generateSubsetsWithDup(result,subset,numsList,0);
        
        result.add(subset);//需要加入空集
        return result;
    }
    
    public void generateSubsetsWithDup(List<List<Integer>> result,List<Integer> subset,List<Integer> numsList,int idx) {
    		//表示放入|不放入第idx元素时的子集序列
    		//先放入idx元素，再对后续元素(idx+1,...)进行处理；
    		//再拿出idx元素，并对后续元素(idx+1,...)进行处理;
    		if(idx==numsList.size())//处理完所有元素
    			return;	
    		subset.add(numsList.get(idx));//放入idx元素
    		//剪枝：
    		//如果结果集中包含该子集，由于原数组是排好序的，所以之后所有的子集均为重复，不需继续执行
    		//对于没有意义的搜索，可采取剪枝。可大幅度提升搜索效率。
    		if(!result.contains(subset)) {
        		result.add(new ArrayList<>(subset));
        		generateSubsetsWithDup(result,subset,numsList,idx+1);//在放入第idx元素的基础上，对后续数组进行处理
    		}
    
    		subset.remove(subset.size()-1);//移除idx元素
    		generateSubsetsWithDup(result,subset,numsList,idx+1);//在不放入第idx元素的基础上，对后续数组进行处理
    }

例3：括号生成

题目描述
给出 n 代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。
解题思路
生成所有的括号组合：n组括号，括号字符串长度为2n，字符串中每个字符有2种选择可能，"(“或”)"，故有2 * 2n种可能。
递归限制条件：
（1）左括号与右括号的数量，最多放置n个
（2）若左括号的数量<=右括号的数量，不可进行放置右括号的递归
则对于长度为2n的括号生成字符串，一次递归表示在第i个位置生成相应的括号。当填满所有位置（i==2 * n）时，则为一个可行的括号生成字符串。
程序代码

    public List<String> generateParenthesis(int n) {
        List<String> result = new ArrayList<String>();//结果集，存储括号生成字符串集合
        List pare = new ArrayList<>();//每个括号生成字符串
        
        generatePare2(0,0,0,n,pare,result);
        
        return result;
    }
    
    public void generatePare(int i,int left,int right,int n,List pare, List<String> result) {
    		//生成括号字符串有2*n个位置，一次递归表示在解空间第i个位置生成相应括号（第left个左括号或第right个右括号）
    		if(i==n*2) {
    			//填充满所有位置（2*n），括号生成完毕，加入结果集
    			String pareStr = "";
    			for(int j=0;j<pare.size();j++)pareStr+=pare.get(j);
    			result.add(pareStr);
    			return;
    		}
    		
    		if(left<n) {
    			//如果左括号数目
    			pare.add("(");//第i个位置加入左括号
    			generatePare(i+1,left+1,right,n,pare,result);//对第i+1个位置生成相应的括号
    			pare.remove(pare.size()-1);//第i个位置取出左括号
    		}
    		
    		if(right<n && left>right) {
    			//如果右括号数目右括号数目，则可加入右括号
    			pare.add(")");//第i个位置加入右括号
    			generatePare(i+1,left,right+1,n,pare,result);//对第i+1个位置生成相应的括号
    			pare.remove(pare.size()-1);//第i个位置取出右括号
    		}
    }

例4：N皇后

题目描述
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

上图为 8 皇后问题的一种解法。
给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。
每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

示例:

输入: 4
输出: [
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]

解释: 4 皇后问题存在两个不同的解法。
解题思路
对于N*N的棋盘，每行都要放置一个且只能放置一个皇后。利用递归对棋盘每一行放置皇后，放置时按列顺序寻找可放置皇后的列。若可放置皇后则将皇后放置该位置，并更新mark标记数组，递归进行下一行皇后放置。当该次递归结束后，恢复mark数组，并尝试下一个可能放置皇后的列。当递归完成N行的N个皇后放置，则将结果保存并返回。
一次递归完成对第i行皇后的放置。
程序代码

    public List<List<String>> solveNQueens2(int n) {
    		List<List<String>> result = new ArrayList<>();//结果数组，存储所有N皇后摆放结果的集合
    		List<List> nQueens = new ArrayList<>();//存放某种N皇后摆放的结果
    		int[][] mark = new int[n][n];//标记棋盘，标记位置是否能拜访皇后的二维数组
    		
    		//初始化
    		for(int i=0;i<n;i++) {
    			List nQueensRow = new ArrayList<>();
    			for(int j=0;j<n;j++) {
    				nQueensRow.add(".");
    				mark[i][j] = 0;
    			}
    			nQueens.add(nQueensRow);
    		}
    		
    		generateNQueens(0,n,nQueens,mark,result);
    		
    		return result;
    }

   public void generateNQueens(int i,int n,List<List> nQueens,int[][] mark,List<List<String>> result){
    		//表示在第i行放置皇后
    		if(i==n) {
    			//将皇后填充完毕（n行皇后均摆放完毕），将N皇后摆放结果加入结果集
    			List<String> nQueensStr = new ArrayList<>();
    			for(int j=0;j<nQueens.size();j++) {
    				List nQueensRow = nQueens.get(j);
    				String nQueensRowStr = "";
    				for(int r=0;r<nQueensRow.size();r++)
    					nQueensRowStr += nQueensRow.get(r);
    				nQueensStr.add(nQueensRowStr);
    			}
    			result.add(nQueensStr);
    			return;
    		}
    		
    		for(int j=0;j<n;j++) {
    			//标记棋盘第i行若有可放置皇后的位置（mark[i][j]==0），在该位置放置皇后
    			if(mark[i][j]==0) {
    				//记录当前的标记棋盘的镜像，用于回溯时恢复之前状态
    				//采用深复制，保存标记棋盘的数据而非引用（浅复制：保存标记棋盘的引用，同时发生改变）
    				int[][] tmp_mark = new int[n][n];
    				for(int r=0;r<n;r++)
    					for(int s=0;s<n;s++)
    						tmp_mark[r][s] = mark[r][s];
    				
    				put_down_the_queen(i,j,mark);//改变标记棋盘
    				//记录第i行皇后放置位置
    				List nQueensRow = nQueens.get(i);
    				nQueensRow.set(j, "Q");
    				nQueens.set(i, nQueensRow);
    				
    				generateNQueens(i+1,n,nQueens,mark,result);//在第i+1行放皇后
    				//回溯，将皇后拿出
    				mark = tmp_mark;//恢复标记棋盘
    				//恢复第i行皇后放置位置
    				nQueensRow.set(j, ".");
    				nQueens.set(i, nQueensRow);
    			}
    		}
    }

    public void put_down_the_queen(int x,int y,int[][] mark) {
    		final int dx[] = {-1,1,0,0,-1,-1,1,1};//纵轴方向数组
    		final int dy[] = {0,0,-1,1,-1,1,-1,1};//横轴方向数组
    		mark[x][y] = 1;//（x,y）放置皇后，进行标记
    		
    		//新的位置向8个方向延伸，每个方向向外延伸1到N-1
    		for(int i=1;i<mark.length;i++) {
    			for(int j=0;j<8;j++) {
    				int new_x = x + i*dx[j];
    				int new_y = y + i*dy[j];
    				
    				if(new_x >= 0 && new_x < mark.length && new_y >= 0 && new_y < mark.length) {
    					//检查新位置是否在棋盘内
    					mark[new_x][new_y] = 1;
    				}
    			}
    		}
    }

例5：火柴棍摆正方形（473）

题目描述
还记得童话《卖火柴的小女孩》吗？现在，你知道小女孩有多少根火柴，请找出一种能使用所有火柴拼成一个正方形的方法。不能折断火柴，可以把火柴连接起来，并且每根火柴都要用到。

输入为小女孩拥有火柴的数目，每根火柴用其长度表示。输出即为是否能用所有的火柴拼成正方形。

示例 1:

输入: [1,1,2,2,2]
输出: true

解释: 能拼成一个边长为2的正方形，每边两根火柴。
示例 2:

输入: [3,3,3,3,4]
输出: false

解释: 不能用所有火柴拼成一个正方形。

算法思路
（1）回溯算法
想象正方形的4条边即为4个桶，将每个火柴杆回溯的放置在每个桶中，在放完n个火柴杆后，检查4个桶中的火柴杆长度和是否相同，相同返回真，否则返回假；在回溯过程中，如果当前所有可能向后的回溯，都无法满足条件，即递归函数最终返回假。
（2）回溯算法中优化/剪枝——超时限制
优化1：n个火柴杆的总和对4取余需要为0，否则返回假。
优化2：火柴杆按照从大到小的顺序排序，先尝试大的减少回溯可能。
优化3：每次放置时，每条边上不可放置超过总和的1/4长度的火柴杆
程序代码

   public boolean makesquare(int[] nums) {
    		int[] square = {0,0,0,0}; // square存储各边的所摆火柴棍长度,并初始化正方形四条边所在桶均为0
    		if(nums == null || sum(nums)==0 || sum(nums)%4!=0)return false;	// 数组长度为0 或者 火柴棍无法成为一个正方形
    		Integer squareLength = sum(nums)/4;
    		Arrays.sort(nums);
    		reverse(nums);	// 降序排序
    		boolean result = generateSquare(0,squareLength,nums,square);
        return result;
    }
    
    public boolean generateSquare(int i, int squareLength, int[] nums, int[] square) {
    		// 将第i个火柴棍连接
    		if(i == nums.length)  // 已将所有火柴棍摆完，若所有边均满足正方形长度，则可摆成一个正方形
    			return square[0] == squareLength && square[1] == squareLength && square[2] == squareLength && square[3] == squareLength;
    		
    		for(int j=0;j<4;j++) { // 将火柴棍逐个加到各个边上
    			if(square[j] + nums[i] <= squareLength) {
    				square[j] += nums[i];	// 若长度不够，则将火柴棍添加到该边上
    				if(generateSquare(i+1, squareLength, nums, square))return true; // 连接第 i+1 个火柴棍
    				square[j] -= nums[i];	// 回溯，将该火柴棍放在其他边上
    			}
    		}
    		return false;	// 该火柴棍没法放在任一一条边上，则返回false，表示该放置方式（路径）错误
    }
    
    public int sum(int[] nums) {
    		int sum = 0;
    		for(int i=0;i

剑指Offer

例1：矩阵中的路径（64）

题目描述
请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向左，向右，向上，向下移动一个格子。如果一条路径经过了矩阵中的某一个格子，则之后不能再次进入这个格子。 例如 a b c e s f c s a d e e 这样的3 X 4 矩阵中包含一条字符串"bcced"的路径，但是矩阵中不包含"abcb"路径，因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后，路径不能再次进入该格子。
解题思路
对于字符串中第i个字符，在矩阵中进行寻找。除了第一个元素外（解空间为整个矩阵），其余每个字符在上一个字符的基础上有上、下、左、右四种选择（解空间为上一个位置上、下、左、右）。如果找到字符，则将字符加入路径，并进行第i+1个字符的查找。如果找不到则回溯，重新选择第i个字符。
程序代码
法1

    //上下左右方向数组
    final int[] to_x = {-1,1,0,0};
    final int[] to_y = {0,0,-1,1};
    
    public boolean hasPath(char[] matrix, int rows, int cols, char[] str)
    {
    		int[][] mark = new int[rows][cols];//标记矩阵，标记包含字符串的路径，1表示路径包含该位置，0表示不包含
    		char[][] _matrix = new char[rows][cols];//将矩阵字符串转换为二维数组形式
    		//初始化
    		for(int i=0,k=0;i<rows;i++)
    			for(int j=0;j<cols;j++)
    			{
    				mark[i][j] = 0;
    				_matrix[i][j] = matrix[k];
    				k++;
    			}
    		List result = new ArrayList<>();//结果数组，存储标记矩阵/存储所有路径
    		
    		//初始化，先找第一个元素(第一个元素在整个矩阵空间上进行搜索),其余元素则在上、下、左、右四个方向进行搜索
    		for(int i=0;i<rows;i++)
    			for(int j=0;j<cols;j++) {
    				if(_matrix[i][j] == str[0]) {
    					mark[i][j] = 1;//标记矩阵记录第一个元素位置
    					backTraceHasPath(_matrix,mark,str,result,rows,cols,i,j,1);
    					mark[i][j] = 0;//恢复标记矩阵
    				}
    			}
    		
    		if(result.size()!=0)
    			return true;//结果集存在对应字符串路径
    		else return false;
    }
    
    public void backTraceHasPath(char[][] matrix,int[][] mark,char[] str,List result,int rows,int cols,int x,int y,int i) {
    		//判断在当前矩阵上下左右移动是否能继续寻找到包含字符串str中第i个元素的路径，如果可以则记录该路径；如果不可以则回溯重新选择
    		if(i==str.length) {
    			//寻找到了包含字符串str中所有元素的一条路径
    			//深复制路径的标记数组
    			int[][] path_mark = new int[rows][cols];
    			for(int r=0;r<rows;r++)
    				for(int s=0;s<cols;s++)
    					path_mark[r][s] = mark[r][s];
    			
    			result.add(path_mark);//将路径的标记数组记录下来
    			return;
    		}
    		
    		//判断向上下左右四个方向移动是否能寻找到字符串str中第i个元素
    		for(int j=0;j<4;j++) {
    			int new_x = x+to_x[j];
    			int new_y = y+to_y[j];
    			if(new_x>=0 && new_x<rows && new_y>=0 && new_y<cols) {
    				//在矩阵范围内移动
    				if(matrix[new_x][new_y] == str[i] && mark[new_x][new_y]==0) {
    					//找到字符串第i个元素 且 第一次进入该格子
    					mark[new_x][new_y]=1;//标记数组标记新的路径
    					backTraceHasPath(matrix,mark,str,result,rows,cols,new_x,new_y,i+1);//记录新位置，进行对第i+1个元素路径的搜索
    					mark[new_x][new_y]=0;//回溯，标记数组恢复原来路径
    				}
    			}
    		}
    }

法2

	// 64.矩阵中的路径
	// 请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。
	// 路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向左，向右，向上，向下移动一个格子。
	// 如果一条路径经过了矩阵中的某一个格子，则该路径不能再进入该格子。
	// 例如 a b c e s f c s a d e e 矩阵中包含一条字符串"bcced"的路径，
	// 但是矩阵中不包含"abcb"路径，因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后，路径不能再次进入该格子。
    int[][] visited;			// 访问数组，判断是否访问
    char[][] realMaxtrix;	// 矩阵的二维数组表示
    int[] dx = {-1,1,0,0};	// 位移数组，依次对应上下左右
    int[] dy = {0,0,-1,1};
    char[] buildPath;			// 通过遍历矩阵构造的字符串
    int idx = 0;					// 填充字符串第idx位置字符
	public boolean hasPath2(char[] matrix, int rows, int cols, char[] str)
    {
		buildPath = new char[str.length];
		visited = new int[rows][cols];
		realMaxtrix = new char[rows][cols];
		int charIdx = 0;
		for(int i=0;i<rows;i++)
			for(int j=0;j<cols;j++)
				{
					visited[i][j] = 0;
					realMaxtrix[i][j] = matrix[charIdx++];
				}
		// 找到符合条件的首字符位置，开始遍历矩阵观察是否能构造出对应的路径
		for(int i=0;i<rows;i++)
			for(int j=0;j<cols;j++)
				if(str[0] ==realMaxtrix[i][j] && buildPathByVisitingMatrix2(i,j,realMaxtrix,rows,cols,str))
			return true;
		
		return false;
    }
	
	public boolean buildPathByVisitingMatrix2(int i,int j,char[][] matrix, int rows, int cols, char[] str) {
		// 采用回溯法访问matrix[i,j]是否 包含在路径中
		// 只有同时满足一下条件才能够继续遍历矩阵：
		// 1. 遍历位置[i,j]位于矩阵内部
		// 2. 当前遍历的节点值满足字符串当前遍历的值
		// 3. 当前节点未访问
		if(i>=0 && j>=0 && i<rows && j<cols && matrix[i][j] == str[idx] && visited[i][j]==0) {
			buildPath[idx] = str[idx];
			visited[i][j] = 1;
			idx++;
			if(idx == str.length)return true;	// 如果此时已遍历完字符串所有字符，则存在路径
			for(int k=0;k<4;k++) {				// 否则从四个方向继续访问matrix[i,j]是否 包含在路径中，若该方向继续遍历可以找到对应路径，则返回true
				if(buildPathByVisitingMatrix2(i+dx[k],j+dy[k],matrix,rows,cols,str))return true;	
			}
			// 回溯时将当前状态恢复
			idx--;
			visited[i][j] = 0;        
		}
		return false;
	}

例2：机器人的运动范围（65）

题目描述
地上有一个m行和n列的方格。一个机器人从坐标0,0的格子开始移动，每一次只能向左，右，上，下四个方向移动一格，但是不能进入行坐标和列坐标的数位之和大于k的格子。 例如，当k为18时，机器人能够进入方格（35,37），因为3+5+3+7 = 18。但是，它不能进入方格（35,38），因为3+5+3+8 = 19。请问该机器人能够达到多少个格子？
解题思路
基础的路径问题，采用回溯法解决。对于每个位置，均有四个方向移动。从坐标（0,0）开始移动，因此共有2个选择：向下移动（x+1）或向右移动（y+1）。
若移动后仍位于矩阵内部且满足行坐标与列坐标数位和不大于threshold且该位置是第一次访问，则进行移动并记录坐标位置。并进行下一个位置的选择。
程序代码

    public int movingCount(int threshold, int rows, int cols)
    {
    		//根据题设实际要求，若阈值<0，则机器人无法到达任何格子
    		if(threshold<0)return 0;
    		//初始化
        int[][] result = new int[rows][cols];//标记数组，记录机器人所能到达的所有格子
        int sum = 0;
        for(int i=0;i<rows;i++)
        		for(int j=0;j<cols;j++)
        			result[i][j] = 0;
        result[0][0] = 1;
        
        backTraceMovingCount(0,0,result,rows,cols,threshold);//从坐标（0，0）开始移动
        
        for(int i=0;i<rows;i++)
    			for(int j=0;j<cols;j++)
    				if(result[i][j]==1)sum++;
        
        return sum;
    }
    
    public void backTraceMovingCount(int x,int y,int[][] result,int rows,int cols,int threshold) 
    {
    			//从当前坐标(x,y)开始移动，只有2种选择，要么向下移动（y+1）要么向右移动（x+1）
    			int new_x = x + 1;
    			int new_y = y + 1;
    			//如果移动后的新位置
    			//1.位于矩阵内部
    			//2.没有走过
    			//3.数位和
    			//则进行移动，并记录。之后进行下一位置的选择
    			if(new_x>=0 && new_x<rows && result[new_x][y]==0 && sum_bit(new_x,y)<=threshold) {
    				//向下移动
    				result[new_x][y] = 1;
    				backTraceMovingCount(new_x,y,result,rows,cols,threshold);//从新坐标(new_x,y)开始移动
    			}
    			
    			if(new_y>=0 && new_y<cols && result[x][new_y]==0 && sum_bit(x,new_y)<=threshold) {
    				//向右移动
    				result[x][new_y] = 1;
    				backTraceMovingCount(x,new_y,result,rows,cols,threshold);//从新坐标(x,new_y)开始移动
    			}
    }
    
    public int sum_bit(int x,int y) {
    		//返回x,y各个位的值的和
    		int sum = 0;
    		int _x = x;
    		int _y = y;
    		
    		while(_x!=0) {
    			sum += _x%10;
    			_x = _x/10;
    		}
    		
    		while(_y!=0) {
    			sum += _y%10;
    			_y = _y/10;
    		}
    		return sum;
    }

法2

  int[] dx = {1,0};
	int[] dy = {0,1};		// 位移的偏移值，只能向右和向下移动
	int[][] visited;			// 二维数组表示，visited[i][j]=0表示未访问，1标识已访问,防止重复访问
	int count = 0;			// 能到达的格子总数
	public int movingCount(int threshold, int rows, int cols)
    {
     解法2：贪心+剪枝
     1. 从（0，0）结点开始，每次只向右向下访问
     2. 若该结点的横纵坐标满足位数和<threshold，则将该结点加入结果集，并继续遍历
    	 3. 不满足条件的不继续遍历（因为每次向下向右只能增大数位和）
		if(threshold<0)return 0;
        visited = new int[rows][cols];
        for(int i=0;i<rows;i++)
        		for(int j=0;j<cols;j++)
        			visited[i][j] = 0;
        countMoving(0,0,threshold,rows,cols);
        return count;
    }
	
	public void countMoving(int i,int j,int threshold,int rows,int cols) {
		// 求可以到达visited[i][j]的格子数目                  
		if(i>=0 && j>=0 && i<rows && j<cols && isPositionSatisfyThreshold(i,j,threshold)) {
			System.out.println("x = "+i +",y = "+j);
			if(visited[i][j]==0){
				count++;
				visited[i][j] = 1;
				for(int k=0;k<2;k++) // 分别向右下两个方向继续访问
					countMoving(i+dx[k],j+dy[k],threshold,rows,cols);
			}
		}
	}
	
	public boolean isPositionSatisfyThreshold(int i,int j, int threshold) {
		int bitSum = 0;
		while(i>0) {
			bitSum += i%10;
			i = i/10;
		}
		while(j>0) {
			bitSum += j%10;
			j = j/10;
		}
		if(bitSum > threshold)return false;
		else return true;
	}

例3：把数组排成最小的数（32）

题目描述
输入一个正整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。例如输入数组{3，32，321}，则打印出这三个数字能排成的最小数字为321323。
程序代码

    // 32.把数组排成最小的数
    // 输入一个正整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。
    // 例如输入数组{3，32，321}，则打印出这三个数字能排成的最小数字为321323。
	List<Long> numbers_array = new ArrayList<Long>();		//存储全排列结果
    public String PrintMinNumber(int [] numbers) {
    	// 1.通过回溯法获取所有数组的全排列结果
    	// 2.比较全排列结果，取最小值
    	// 3.因为是字符串排列所以用Long类型存储（Integer范围）
    		if(numbers == null || numbers.length == 0)return null;
    		Long minValue = Long.MAX_VALUE;
    		boolean[] visited = new boolean[numbers.length];
    		for(int i=0;i<numbers.length;i++)visited[i] = false;
    		
    		List<Integer> number_array = new ArrayList<Integer>(); 
    		getMinValueOfArray(0,numbers,visited,number_array);
    		for(int i=0;i<numbers_array.size();i++) 
    			if(numbers_array.get(i)<minValue)minValue = numbers_array.get(i);
    		return minValue.toString();
    }
    
    public void getMinValueOfArray(int i, int[] arrays, boolean[] visited, List<Integer> number_array) {
    	// 向全排列数组中加入第i个位置的数字
    		if(i == arrays.length) {
    			// 此时已经填完所有数组，构成一个字符串，加入结果数组
    			StringBuilder sb = new StringBuilder();
    			for(int j=0;j<number_array.size();j++)sb.append(number_array.get(j));
    			numbers_array.add(Long.parseLong(sb.toString()));
    		}else {
    			for(int j=0;j<arrays.length;j++) {
    				if(!visited[j]) {
    					number_array.add(arrays[j]);
    					visited[j] = true;
    					getMinValueOfArray(i+1,arrays,visited,number_array);
    					visited[j] = false;
    					number_array.remove(number_array.size()-1);
    				}
    			}
    		}
    		
    }

例4：字符串的排列（27）

题目描述
输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。
输入描述:
输入一个字符串,长度不超过9(可能有字符重复),字符只包括大小写字母。
程序代码
法1：

	// 27. 字符串排列
	// 输入一个字符串,按字典序打印出该字符串中字符的所有排列。
	// 例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。
	Set result = null; 					// 结果数组，存储全排列字符串结果，采用Set存储，防止出现重复的全排列字符串
	List permutation = null;			// 全局字符串（记录某个全排列字符串）
	boolean[] visited = null;					// 访问数组，记录某个字符是否访问
    public ArrayList Permutation(String str) {
    		if(str == null || str.length() == 0)return new ArrayList();
    		
    			result = new HashSet();	
    			visited = new boolean[str.length()];
    			permutation = new ArrayList();
    			for(int i=0;i result_arr = new ArrayList(result);
    		Collections.sort(result_arr);
    		
    		return result_arr;
    }
    
    public void concretPermutation(int i,String str) {
    		// 填充构造字符串第i个位置
    		// 若当前处理的位置i == 原字符串长度（说明当前已经构造出一个全排列字符串）
    		// 将该字符串加入结果集
    		// 否则遍历原字符串中每一个字符
    		// 若该字符未加入构造字符串，则加入构造字符串，并且标记访问数组，并继续填充下一位置i+1
    		// 处理结束后恢复现场：将当前位置字符取出，访问数组恢复标记
    		if(i == str.length()) {
    			String permu = "";
    			for(int idx=0;idx

法2：

	public ArrayList Permutation(String str) {
	    //输入一个字符串,按字典序打印出该字符串中字符的所有排列。
		//例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。

			       List resultList = new ArrayList<>();
			        if(str.length() == 0)
			            return (ArrayList)resultList;
			        //递归的初始值为（str数组，空的list，初始下标0）
			        fun(str.toCharArray(),resultList,0);
			        Collections.sort(resultList);
			        return (ArrayList)resultList;
			    }
			     
			    private void fun(char[] ch,List list,int i){
			        //这是递归的终止条件，就是i下标已经移到char数组的末尾的时候，考虑添加这一组字符串进入结果集中
			        if(i == ch.length-1){
			            //判断一下是否重复
			            if(!list.contains(new String(ch))){
			                list.add(new String(ch));
			                return;
			            }
			        }else{
			            //这一段就是回溯法，这里以"abc"为例
			             
			            //递归的思想与栈的入栈和出栈是一样的,某一个状态遇到return结束了之后，会回到被调用的地方继续执行
			             
			            //1.第一次进到这里是ch=['a','b','c'],list=[],i=0，我称为 状态A ，即初始状态
			            //那么j=0，swap(ch,0,0)，就是['a','b','c']，进入递归，自己调自己，只是i为1，交换(0,0)位置之后的状态我称为 状态B 
			            //i不等于2，来到这里，j=1，执行第一个swap(ch,1,1)，这个状态我称为 状态C1 ,再进入fun函数，此时标记为T1，i为2，那么这时就进入上一个if，将"abc"放进list中
			            /-------》此时结果集为["abc"]
			             
			            //2.执行完list.add之后，遇到return，回退到T1处，接下来执行第二个swap(ch,1,1)，状态C1又恢复为状态B
			            //恢复完之后，继续执行for循环，此时j=2,那么swap(ch,1,2),得到"acb"，这个状态我称为C2,然后执行fun，此时标记为T2,发现i+1=2,所以也被添加进结果集，此时return回退到T2处往下执行
			            /-------》此时结果集为["abc","acb"]
			            //然后执行第二个swap(ch,1,2)，状态C2回归状态B,然后状态B的for循环退出回到状态A
			             
			            //             a|b|c(状态A)
			            //               |
			            //               |swap(0,0)
			            //               |
			            //             a|b|c(状态B)
			            //             /  \
			            //   swap(1,1)/    \swap(1,2)  (状态C1和状态C2)
			            //           /      \
			            //         a|b|c   a|c|b
			             
			            //3.回到状态A之后，继续for循环，j=1,即swap(ch,0,1)，即"bac",这个状态可以再次叫做状态A,下面的步骤同上
			            /-------》此时结果集为["abc","acb","bac","bca"]
			             
			            //             a|b|c(状态A)
			            //               |
			            //               |swap(0,1)
			            //               |
			            //             b|a|c(状态B)
			            //             /  \
			            //   swap(1,1)/    \swap(1,2)  (状态C1和状态C2)
			            //           /      \
			            //         b|a|c   b|c|a
			             
			            //4.再继续for循环，j=2,即swap(ch,0,2)，即"cab",这个状态可以再次叫做状态A，下面的步骤同上
			            /-------》此时结果集为["abc","acb","bac","bca","cab","cba"]
			             
			            //             a|b|c(状态A)
			            //               |
			            //               |swap(0,2)
			            //               |
			            //             c|b|a(状态B)
			            //             /  \
			            //   swap(1,1)/    \swap(1,2)  (状态C1和状态C2)
			            //           /      \
			            //         c|b|a   c|a|b
			             
			            //5.最后退出for循环，结束。
			             
			            for(int j=i;j

三、分治法

（1）含义
在计算机科学中，分治法是一种很重要的算法。字面上的解释是“分而治之”，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础，如排序算法(快速排序，归并排序)，傅立叶变换(快速傅立叶变换)……
分治法的基本设计思想是：将一个规模为N的大问题，分割成一些规模为K的规模较小的子问题，这些子问题相互独立且与原问题形式相同。递归求出子问题的解后进行合并，就可以得到原问题的解。
分治法也是一种基于递归思想的算法。
（2）基本格式
分治法在每一层递归上有三个步骤：

• step1 分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题。
• step2 求解：若子问题划分得规模较小且容易被解决时则直接解决，否则递归求解各个子问题。
• step3 合并：将各个子问题的解合并为原问题的解。

（3）理解
实际上就是类似于数学归纳法，找到解决本问题的求解方程公式，然后根据方程公式设计递归程序。

1. 一定是先找到最小问题规模时的求解方法；
2. 然后考虑随着问题规模增大时的求解方法（子问题的解可合并为原问题的解）；
3. 找到求解的递归函数式后（各种规模或因子），设计递归程序即可。

（4）基本格式

public void divide(int[] arr,int start,int end){
	if(start >= end)return;
	// 获得分割点
	int dividePoint = getDividePoint(start,end);
	divide(arr,start,dividePoint);	// 递归分割前半部分
	divide(arr,dividePoint+1,end);	// 递归分割后半部分

	merge(arr,start,dividePoint,end);	// 合并前半部分后半部分
}

（5）基本案例
例1：归并排序
归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

    //归并排序的分治---分
    private void divide(int[] arr,int start,int end){
        //递归的终止条件
        if(start >= end)
            return;
        //计算中间值，注意溢出
        int mid = start + (end - start)/2;
 
        //递归分
        divide(arr,start,mid);
        divide(arr,mid+1,end);
 
        //治
        merge(arr,start,mid,end);
    }
 
    private void merge(int[] arr,int start,int mid,int end){
        int[] temp = new int[end-start+1];
 
        //存一下变量
        int i=start,j=mid+1,k=0;
        //下面就开始两两进行比较
        while(i<=mid && j<=end){
            if(arr[i] <= arr[j]){
                temp[k++] = arr[i++];
            }else{
                temp[k++] = arr[j++];
            }
        }
        //各自还有剩余的没比完，直接赋值即可
        while(i<=mid)
            temp[k++] = arr[i++];
        while(j<=end)
            temp[k++] = arr[j++];
        //覆盖原数组
        for (k = 0; k < temp.length; k++)
            arr[start + k] = temp[k];
    }
}

例2：快速排序
快速排序是指通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
一趟快速排序的算法是：

1. 设置两个变量i、j，排序开始的时候：i=0，j=N-1；
2. 以第一个数组元素作为关键数据，赋值给key，即key=A[0]；
3. 从j开始向前搜索，即由后开始向前搜索(j–)，找到第一个小于key的值A[j]，将A[j]和A[i]的值交换；
4. 从i开始向后搜索，即由前开始向后搜索(i++)，找到第一个大于key的A[i]，将A[i]和A[j]的值交换；
5. 重复第3、4步，直到i=j； (3,4步中，没找到符合条件的值，即3中A[j]不小于key,4中A[i]不大于key的时候改变j、i的值，使得j=j-1，i=i+1，直至找到为止。找到符合条件的值，进行交换的时候i， j指针位置不变。另外，i==j这一过程一定正好是i+或j-完成的时候，此时令循环结束）。

   public int[] sortArray(int[] nums) {
    		//对nums进行快排
        quickSort(0,nums.length-1,nums);
        return nums;
    }
    
    public void quickSort(int start,int end,int[] nums) {
    		//对数组nums[left..right]进行快排
    		//left指针为数组初始位置的遍历指针，right为数组末端位置的遍历指针
    		if(start >= end)return;
    		
    		int key = nums[start];//基准
    		int left = start;	 //起始结点
    		int right = end;		 //末端结点
    		
    		while(left<right) {
    			//从末端指针向前遍历，直到遇到第一个小于基准的值，此时将nums[left]与nums[right]交换
    			while(nums[right] >= key && left<right)right--;
    			swapAandB(left,right,nums);
    			//从首端指针向后遍历，直到遇到第一个大于基准的值，此时将nums[left]与nums[right]交换
    			while(nums[left] <= key && left<right)left++;
    			swapAandB(left,right,nums);
    		}
    		
    		//一次遍历结束idx(left=right)左边的元素均idx。此时对idx左右的元素分别进行快排
    		quickSort(start,left-1,nums);
    		quickSort(left+1,end,nums);
    }
    
    public void swapAandB(int a,int b,int[] nums) {
    		//将nums[a]与nums[b]交换
    		int tmp = nums[a];
    		nums[a] = nums[b];
    		nums[b] = tmp;
    }

剑指Offer

例1：数组中的逆序对

题目描述
在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007
输入描述:
题目保证输入的数组中没有的相同的数字

示例1

输入
1,2,3,4,5,6,7,0
输出
7

解题思路
利用归并排序的思想求逆序数个数。
进行归并排序时，当前一个数组第i个元素>后一个数组第j个元素时，插入后一个数组第j个元素。此时前一个数组的第i个元素之后的所有元素均大于第j个元素，故对应逆序数对有mid-i+1个。
程序代码

    int count = 0;//逆序对总数
    public int InversePairs(int [] array) {
    		if(array.length <= 0 || array == null)
    			return 0;
    		//通过对数组进行归并排序计算数组中的逆序数对
    		merge_sort(array,0,array.length-1);
        return count;
    }
    
    public void merge_sort(int[] nums,int left,int right) {
    		//对数组nums[left..right]进行归并排序
    		if(right<=left)return;//数据规模足够小
    		
    		int mid = (left + right)/2;//取中间值
    		
    		merge_sort(nums,left,mid);//对子数组nums[left..mid]进行归并排序
    		merge_sort(nums,mid+1,right);//对子数组nums[mid+1...right]进行归并排序
    		
    		merge_two_list(nums,left,mid,right);
    }
    
    public void merge_two_list(int[] nums,int left,int mid,int right) {
    		//将两个已排序的数组进行顺序合并nums[left,...,mid][mid+1,...,right]
    		//逆序数求解算法思路：
    		//进行归并排序时，插入后一个数组的第j个元素时，该元素相关的逆序数有mid-i+1个（前一个数组第i个元素后的元素均大于第j个元素）
    		int[] nums_tmp = new int[right-left+1];
    		
    		int i = left;
    		int j = mid+1;
    		int k = 0;
    		
    		//对数组A和数组B进行遍历，若数组A中元素i<=数组B中元素j，则将元素i加入辅助数组中；若数组A中元素i>数组B中元素j，则将元素j加入辅助数组中。
    		//此时辅助数组为排好序的数组，用辅助数组覆盖原数组。
    		while(i<=mid && j<=right) {
    			if(nums[i]<=nums[j]) {
    				nums_tmp[k++] = nums[i++];
    			}else {
    				nums_tmp[k++] = nums[j++];
    				//此时两个数组都是已经由小到大排好序了的，所以如果数组A中元素a大于数组B元素b，那么a元素后面的所有元素都大于b，就有mid-i+1个逆序对
    				count = (count+mid-i+1)%1000000007;
    			}
    		}

    		while(i<=mid) {
    			nums_tmp[k++] = nums[i++];//将数组A中未遍历完的元素加入辅助数组中
    		}
    		while(j<=right) {
    			nums_tmp[k++] = nums[j++];//将数组B中未遍历完的元素加入辅助数组中，此时数组A中所有元素均遍历完，均小于数组B中未遍历元素。故没有逆序对
    		}
    		//用辅助数组覆盖原数组
    		for(i=left;i<=right;i++)
    			nums[i] = nums_tmp[i-left];
    }

leetcode

例1：计算右侧小于当前元素的个数

题目描述
给定一个整数数组 nums，按要求返回一个新数组 counts。数组 counts 有该性质： counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。

示例:
输入: [5,2,6,1]
输出: [2,1,1,0]
解释:
5 的右侧有 2 个更小的元素 (2 和 1).
2 的右侧仅有 1 个更小的元素 (1).
6 的右侧有 1 个更小的元素 (1).
1 的右侧有 0 个更小的元素.

解题思路
利用索引数组+归并排序解决。
对于归并排序的每一次归并过程中，当数组1中的元素p1大于数组2中的元素p2时候，则数组1中p1到mid中所有的元素均大于数组2中的元素p2，则这些元素的逆序数均+1。
程序代码

    public List<Integer> countSmaller2(int[] nums) {
		List<RPair> numsList = new ArrayList<>();//原数组对应索引数组
		List<Integer> count = new ArrayList<>();	//结果数组，存储每个元素对应右侧小于当前元素的个数
		//初始化
		for(int i=0;i<nums.length;i++)
		{
			numsList.add(new RPair(nums[i],i));
			count.add(0);
		}
		
		generateCountArrays(0,nums.length-1,numsList,count);
		
		return count;
    }

    public void generateCountArrays(int left,int right,List<RPair> numsList,List count) {
		//对数组numsList[left..right]进行归并排序
		if(left>=right)return;//数组足够小则直接返回
		int mid = (left+right)/2;
		
		generateCountArrays(left,mid,numsList,count);//对左数组归并排序
		generateCountArrays(mid+1,right,numsList,count);//对右数组归并排序
		
		mergeTwoOrderedArrays(left,mid,right,numsList,count);//合并左右数组
	}

	public void mergeTwoOrderedArrays(int left,int mid,int right,List<RPair> numsList,List<Integer> count) {
		//将两个已排序的数组nums[left..mid]，nums[mid+1..right]进行归并
		//进行归并排序时，如果数组2中p2元素小于数组1中p1元素，则也均小于数组1中p1及之后的元素，这些元素的逆序数+1，记录在count数组，并且对原数组重排序
		List<RPair> tempList = new ArrayList<RPair>();//辅助数组
		Integer p1 = left;	//数组1的下标指针
		Integer p2 = mid+1;	//数组2的下标指针
		
		while(p1<=mid && p2<=right) {
			if(numsList.get(p1).value <= numsList.get(p2).value) {
				//数组1的元素p1<=数组2的元素p2，将较小值p1记录于辅助数组
				//存储对象，采用深复制，否则复制的是引用
				tempList.add(new RPair(numsList.get(p1).value,numsList.get(p1).idx));
				p1++;
			}else {
				//数组1的元素p1>数组2的元素p2，将较小值p2记录于辅助数组，并将逆序数个数记录于count数组
				//则对于numsList[p1..mid]中所有元素，均大于p2这个数，它们的逆序数个数+1
				tempList.add(new RPair(numsList.get(p2).value,numsList.get(p2).idx));
				
				for(int i=p1;i<=mid;i++) {
					count.set(numsList.get(i).idx, count.get(numsList.get(i).idx) + 1);
				}
				p2++;
			}
		}
		//对剩余元素进行添加
		while(p1<=mid) {tempList.add(new RPair(numsList.get(p1).value,numsList.get(p1).idx));p1++;}
		//数组1中元素遍历结束，此时数组2中元素均大于数组1中元素，不存在逆序数
		while(p2<=right) {tempList.add(new RPair(numsList.get(p2).value,numsList.get(p2).idx));p2++;}
		//排序后的辅助数组覆盖原数组，进行归并排序
		for(int i=left;i<=right;i++) {
			numsList.set(i, tempList.get(i-left));
		}
	}

	protected class RPair{
	//对应原数组的索引数组，记录下标和值
		Integer value;//值
		Integer idx;//下标
		
		RPair(Integer value,Integer idx) {
			this.value = value;
			this.idx = idx;
		}
	}