c++算法总结

DFS

检索特定路径，应想到DFS。补充一点，数据结构图中，节点的度是指其邻接的变数，有向图中，节点又有入度和出度之分，分表表示被指向和指向的变数。

79单词搜索

检索特定路径，从二维字符里检索特定单词，使用dfs算法，当深度达标后，检索终止。-为了提升速度，要把false的情况，写在前面，及时返回。又是cout也会导致超时。
递归实现的dfs：

int dfs(vector<vector<char>>& board, string word, int i, int j, int depth){
    //cout<
    if(i < 0 || i >= board.size() || j < 0 || j >= board[0].size())
        return false;
    if(board[i][j] != word[depth])//先把false写前面，防止超时
        return false;
    if(depth >= word.size() - 1)
        return true;
    
    //cout<<"7 line"<
    board[i][j] ='!';
    bool res = dfs(board, word, i-1, j, depth+1) || dfs(board, word, i+1, j, depth+1) ||dfs(board, word, i, j-1, depth+1)\
    ||dfs(board, word, i, j+1, depth+1);
    board[i][j] = word[depth];
    return res;
}
class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {
        for(int i = 0; i < board.size(); i++){
            for(int j = 0; j < board[0].size(); j++){
                
                    //board[i][j] = '!';
                if(dfs(board, word, i, j, 0))
                    return true;
                    //board[i][j] = word[0];             
            }
        }
        return false;

    }
};

237 二叉树的最近公共祖先

题目属于二叉树，同时使用了DFS求解，自己的思路，使用DFS记录了查找特定节点的路径，然后判断两个节点的的重合路径，找出最近公共祖先。第一次提交超时没过，原因是从上至下添加节点，做了一些无用功，修改后，从下至上记录路径，当找到目标后才会添加进去，记录下这个特定路径

class Solution {
public:
    int dfsTree(TreeNode* root, TreeNode* p, vector<TreeNode*>& path){
        if(root == p){
            path.push_back(root);
            return 0;
        }
        if(root == NULL)
            return -1;

        if(!dfsTree(root->left, p, path) || !dfsTree(root->right, p, path)){
            path.push_back(root);
            return 0;
        }
        return -1;
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        vector<TreeNode*> pPath, qPath;
        dfsTree(root, p, pPath);
        dfsTree(root, q, qPath);

        TreeNode* resNode = pPath[0];
        int qLen = qPath.size();
        int pLen = pPath.size();
        for(int i = 0; i < min(qLen, pLen); i++){
            if(pPath[pLen -1 -i]->val == qPath[qLen - 1 -i]->val)
                resNode = pPath[pLen -1 -i];
            else
                break;
        }
        return resNode;        
    }
};

207课程表

437 路径综合Ⅲ

求二叉树中和为N的路径总数，路径可以从任意节点开始，路径从上到下且连续。因为路径不是必须包含根节点，可以是其他节点开始，所以增加了一层难度，所以本题目用dfs实现，但是用了两层递归。

class Solution {
public:
    int pathSum(TreeNode* root, int sum) {
         if(root == NULL) return 0;
         return dfs(root, sum) + pathSum(root->left, sum) + pathSum(root->right, sum);
     }
    int dfs(TreeNode* root, int sum){  //该节点开始的和为sum的路径
         int res = 0;
         if(root == NULL) return res;
         if(sum == root->val)
             res++;
         res+=dfs(root->left,sum - root->val);
         res+=dfs(root->right,sum - root->val);
         return res;
     }
 };

494 目标和

在数组中添加正负号，使所有数的和加起来等于目标值，一共有多少组这样的正负号情况，首先想到的是DFS，到最底层递归的和满足目标值即可，自己想的思路，时间复杂度较高。

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        return dfs(nums, target, 0);
    }
    int dfs (vector<int>& nums, int target, int depth){
        int res = 0;
        if(depth == nums.size()){
            if(0 == target)
                return 1;
            else
                return 0;
        }
        //递归当前位置是正号和负号的情况
        res = dfs(nums, target - nums[depth], depth + 1) + dfs(nums, target + nums[depth], depth + 1);
        return res;
    }
};

541 二叉树的直径

其实就是求二叉树左右节点的深度和，并求出最大值。用递归DFS实现即可

class Solution {
public:
    int diameterOfBinaryTree(TreeNode* root) {
        int maxPath = 0;
        countPath(root, maxPath);
        return maxPath;
    }

    int countPath(TreeNode* root, int& maxPath){
        if(root == NULL)
            return 0;
        int leftDepth = countPath(root->left, maxPath);
        int rightDetph = countPath(root->right, maxPath);
        int tempPath = leftDepth + rightDetph;  //当前节点直径
        maxPath = max(maxPath, tempPath);   //是否更新最大直径
        return max(leftDepth, rightDetph) + 1;  //返回当前节点深度
    }
};

399 除法求值

题意比较复杂，建议参考原题。使用邻接表构建有向图，然后dfs特定起始点路径的权重和，还使用列stl的pair，思路没想到，一旦知道了思路，就比较直观的实现就行了

class Solution {
public:
    vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
        map<string, vector <pair<string, double>>> neibourTable;
        //构建邻接表
        for(int i = 0; i < equations.size(); i++){
            neibourTable[equations[i][0]].push_back(make_pair(equations[i][1], values[i]));
            neibourTable[equations[i][1]].push_back(make_pair(equations[i][0], 1 / values[i]));
        }

        vector<double> res(queries.size());
        map<string, bool> used;
        for(int i = 0; i < queries.size(); i++){
            //图中不存在的节点
            if(!neibourTable.count(queries[i][0]) || !neibourTable.count(queries[i][1])){
                res[i] = -1.0;
            }
            else{
                res[i] = dfsWeight(neibourTable, queries[i][0], queries[i][1], used);
                if(abs(res[i]) < 1e-6) //没有这个路径，要填-1
                    res[i] = -1.0;
            }
        }
        return res;
    }

    double dfsWeight(map<string, vector <pair<string, double>>> neibourTable, string& current, string& target, map<string, bool>& used){
        if(current == target)
            return 1.0;
        for(auto weightPair: neibourTable[current]){
            if(used.count(weightPair.first) != 0 && used[weightPair.first] == true) //被访问过
                continue;
            used[weightPair.first] = true; //visited
            double res = dfsWeight(neibourTable, weightPair.first, target, used);
            used[weightPair.first] = false; //no visited
            if(abs(res) > 1e-6)  //正确的路径
                return res * weightPair.second;   
        }
        return 0.0;
        
    }

};

129求根节点到叶节点数字之和

二叉树所有节点都是个位数，求所有路径组成的数字之和，比如两条路径（1 2; 1 3），和就是12+13=25，用递归dfs实现，当是叶子节点的时候就进行处理

class Solution {
public:
    void dfsSum(TreeNode* root, int nums, int& sum){
        if(!root)
            return;
        nums = nums * 10 + root->val;
        if(root->left == NULL && root->right == NULL){
            sum += nums;
            return;
        }
        if(root->left) //递归穿参节点非空
            dfsSum(root->left, nums, sum);
        if(root->right)
            dfsSum(root->right, nums, sum);
    }
    int sumNumbers(TreeNode* root) {
        int nums = 0, sums = 0;
        dfsSum(root, nums, sums);
        return sums;
    }
};

BFS

优先从宽度或层的维度进行搜索。只要是找到什么的最短距离一般就应想到BFS，层序遍历也是比较经典的应用（参考下文的102题）

542矩阵

01组成的矩阵，找出每个位置离0的最短距离。直观想法是对每个位置进行BFS，找出到0的最短距离，自己实现了，逻辑是对的，但是某些大的用例超时了。

class Solution {
public:
    int minDepthBfs(vector<vector<int>>& mat, int i, int j){
        if(mat[i][j] == 0)
            return 0;
        int depth = 0;
        vector<vector<int>> used = mat;
        queue<vector<int>> q;
        vector<int> coordinate;
        q.push({i, j});
        while(!q.empty()){
            int len = q.size();
            for(int i = 0; i < len; i++){
                coordinate = q.front();
                q.pop();
                int x = coordinate[0];
                int y = coordinate[1];
                
                if(x < 0 || y < 0 || x >= mat.size() || y >= mat[0].size() || used[x][y] == -1)
                    continue;
                used[x][y] = -1;
                if(mat[x][y] == 0){
                    return depth;
                }

                q.push({x - 1, y});
                q.push({x + 1, y});
                q.push({x, y - 1});
                q.push({x, y + 1});
            }
            depth++;
        }
        return depth;
    }
    vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
        vector<vector<int>> res = mat;
        for(int i = 0; i < mat.size(); i++){
            for(int j = 0; j < mat[0].size(); j++){
                res[i][j] = minDepthBfs(mat, i, j);
            }
        }
        return res;
    }
};

上面的程序不对，按照这个思路重新调试一下，逻辑应该没问题了，部分用力超时。本质上是最短路径长度，最简单的bfs。bfs的实现关键是一个队列，一个while，一个for循环，wile控制遍历所有节点，for控制深度，一次for循环走完，遍历完这个深度的所有节点。
注意：
for循环反范围是0–目前队列长度，但是q.size()不能直接写到for循环里，因为for循环里面会改变队列长度！
used矩阵控制哪些已经被遍历了，最好是入队时改变状态标明已被遍历，而不要出队时再改变
注意边界 >=0，

class Solution {
public:
    int bfsDepth(vector<vector<int>>& mat, int i, int j){
        int depth = 0;
        if(mat[i][j] == 0)
            return 0;
        vector<vector<int>> used = mat;
        vector<int> cor;
        queue<vector<int>> q;
        q.push({i,j});
        used[i][j] = 2;        
        while(!q.empty()) {           
            int len = q.size();
            for(int k = 0; k < len; k++){                
                cor = q.front();
                q.pop();
                
                if(mat[cor[0]][cor[1]] == 0)
                    return depth;

                // used[cor[0]][cor[1]] = 2;
                if(cor[0]+1 < mat.size() && used[cor[0]+1][cor[1]] != 2){
                    q.push({cor[0]+1, cor[1]}); 
                    used[cor[0]+1][cor[1]] = 2;
                }
                if(cor[0]-1 >= 0 && used[cor[0]-1][cor[1]] != 2) {       
                    q.push({cor[0]-1, cor[1]});
                    used[cor[0]-1][cor[1]] = 2;
                }
                if(cor[1]+1 < mat[0].size() && used[cor[0]][cor[1]+1] != 2){
                    q.push({cor[0], cor[1]+1});
                    used[cor[0]][cor[1]+1] = 2;
                }
                if(cor[1]-1 >= 0 && used[cor[0]][cor[1]-1] != 2){
                    q.push({cor[0], cor[1]-1});  
                    used[cor[0]][cor[1]-1] = 2;  
                }
            }            
            depth++; //这里加深度！
        }
        return depth;
    }
    vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
        vector<vector<int>> res = mat;
        for(int i = 0; i < mat.size(); i++){
            for(int j = 0; j < mat[0].size(); j++){
                res[i][j] = bfsDepth(mat, i, j);
            }
        }
        return res;
    }
};

207课程表

题意实际就是：给一个图，判断一个图中是否存在环。看别人的思路通过图的拓扑排序来完成，可以通过BFS或DFS实现，下面是别人的代码，我会自己再实现一遍。另外，邻接表和邻接矩阵也了解下，下面的程序使用了入度数组和邻接表构建图

class Solution {
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        //验证是否为DAG，每次验证指向的是否已经存在于当前图中
        
        //建图
        vector<int> indegree(numCourses,0);//入度
        vector<vector<int>> graph(numCourses,vector(0,0));//邻接表

        for(int i=0;i<prerequisites.size();i++){
            indegree[prerequisites[i][1]]++;
            graph[prerequisites[i][0]].push_back(prerequisites[i][1]);
        }
        //显示图
        showgraph(graph,numCourses);
        //BFS
        queue<int> q;
        for(int i=0;i<numCourses;i++){
            if(indegree[i]==0){
                q.push(i);
            }
        }
        //将入度为0的点且未访问过的进入set，然后将其后继的入度全部减一，循环执行
        int cnt=0;
        while(!q.empty()){
            int front=q.front();
            q.pop();
            cnt++;

            for(int j=0;j<graph[front].size();j++){
                int v=graph[front][j];
                indegree[v]--;
                if(indegree[v]==0){  //度为0的节点，送入队列
                    q.push(v);
                }
            }
        }
        return cnt==numCourses;//当有环时，总有一些点入度不能减到0，因此不能完全bfs遍历
    }
private:
    void showgraph(vector<vector<int>>& graph,int numCourses){
        for(int i=0;i<numCourses;i++){
            for(int j=0;j<graph[i].size();j++){
                cout<<graph[i][j]<<",";
            }
            cout<<endl;
        }
    }
};

112路径总和

给一个二叉树和整数，如果存在跟节点到叶子节点这样的路径，路径之和等于该整数，则返回true。这个题比较简单，用dfs/bfs都行，这里使用bfs实现的，dfs实现更简单

struct TreeVal {
    TreeNode* node;
    int value;
    TreeVal(TreeNode* n, int x) : node(n), value(x) {} 
};

class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root == NULL)
            return false;
        queue<TreeVal*> q;
        TreeVal* temp = new TreeVal(root, targetSum);
        q.push(temp);
        while(!q.empty()) {
            int len = q.size();
            for(int i = 0; i < len; i++) {
                TreeVal* cur = q.front();
                q.pop();
                if(cur->node == NULL){
                    continue;
                }
                //满足条件，且当前节点是叶子节点
                if(cur->value == cur->node->val && !cur->node->left && !cur->node->right)
                    return true;

                TreeVal* tLeft = new TreeVal(cur->node->left, cur->value - cur->node->val);
                q.push(tLeft);
                TreeVal* tRitht = new TreeVal(cur->node->right, cur->value - cur->node->val);
                q.push(tRitht);
            }
        }
        return false;
    }
};

动态规划

转移方程比较难想，经典的背包问题应该掌握
dp[i][j]表示将前i种物品装进限重为j的背包可以获得的最大价值, 0<=i<=N, 0<=j<=W
01背包：dp[i][j] = max(dp[i−1][j], dp[i−1][j−w[i]]+v[i]) // j >= w[i]
完全背包：dp[i][j] = max(dp[i−1][j], dp[i][j−w[i]]+v[i]) // j >= w[i]
完全背包与01背包的唯一不同就是max第二项不是dp[i-1]而是dp[i]，此外还有多重背包，即区别于完全背包，每样物品的个数不是无限的，是有特定个数。
动态规划思路比较难想，要有维度扩充的观念，背包问题是扩充了dp维度，还有一些问题需要扩充时间维度，不能简单的由上一个状态，直接推出下一个状态，状态的推进有时需要遍历实现，如332，遍历钱币数组。

139单词分解

输入: s = “leetcode”, wordDict = [“leet”, “code”]
输出: true
解释: 返回 true 因为 “leetcode” 可以被拆分成 “leet code”
判断句子是否可以被这些单词分解，返回true或false，直观的想法是建立一个以首字母为key的单词哈希表，然后遍历句子s，根据首字母到hash表查找对应单词，找到后继续往下找，找不到返回false，这种方法直观，但是复杂的用例过不去，因为并没有完备地尝试所有的可能。

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        map<char, vector<string>> key_word;
        for(auto word:wordDict){
            if(key_word.count(word[0]))
                key_word[word[0]].push_back(word);
            else{
                vector<string> temp_vec = {word};
                key_word[word[0]] = temp_vec;
            }            
        }

        int index = 0;
        while(index < s.length()){
            if(key_word.count(s[index])){
                int flag = 0;
                for(auto word:key_word[s[index]]){
                    if(s.length()-index >= word.length() && word.compare(0, word.length(), s, index, word.length()) == 0){
                        index += word.length();
                        flag = 1;
                        break;
                    }
                }
                cout<<index<<flag<<endl;
                if(flag == 0)
                    return false;
            }
            else
                return false;
        }
        if(index >= s.length())
            return true;
        else
            return false;
    }
};

参考别人的思路，比较常见的是用动态规划解决，定义了一个数组，存储句子s第前i个位置能否被合成。两层for循环，逻辑就是如果前j个位置可以合成，字典中有单词和j到i的位置匹配，那么前i个位置也可以合成
参考别人结题思路

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        int l = s.length();
        //bool isWordBreak[1000] = {false};
        vector<bool> isWordBreak(l + 1, false);
        isWordBreak[0] = true;

        set<string> wordSet;
        for(auto word:wordDict){
            wordSet.insert(word);
        }

        for(int i = 0; i < l + 1; i++){
            for(int j = 0; j < i; j++){
                if(!isWordBreak[j]) ///假设j不是已知的断点，不用继续判断
                    continue;
                if(wordSet.find(s.substr(j, i-j)) != wordSet.end()){
                    isWordBreak[i] = true;
                    break;
                }
            }
        }
        return isWordBreak[l];   
    }
};

279 完全平方数

给定一个数，找到若干个完全平方数（比如 1, 4, 9, 16, …）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。一看可能就是dp，但是想不出来转移方程。看了别人的思路，dp[n] = min(dp[n-j*j] + 1, dp[n])，思路很简单，比如给定100，我们可以计算我们可以由100-1或100-4或100-9等的结果得到

class Solution {
public:
    int numSquares(int n) {
        vector<int> dp(n + 1, 10000);  //dp初始化一个比较大的数，确保转移方程正确
        dp[0] = 0;
        for(int i = 1; i <=n; i++){
            int squareRoot = sqrt(i);
            for(int j = 1; j <= squareRoot; j++){
                dp[i] = min(dp[i], dp[i - j * j] + 1);
            }
        }
        return dp[n];
    }
};

300 最长递增子序列

求数组的最长递增子序列，子序列可以不连续。看到这个题目感觉是要用动态规划，转移方程想不出。参考别人思路，定义dp[i]，表示以第i个数结尾的最长子序列，注意并不是前i个数的最长子序列！求dp[i]的时候，逐个对前面的数进行遍历，dp[i] = max(dp[i], dp[j] + 1);

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        vector<int> dp(nums.size(), 1);
        for(int i = 1; i < nums.size(); i++){
            for(int j = 0; j < i; j++){
                if(nums[j] < nums[i])
                    dp[i] = max(dp[i], dp[j] + 1);
            }
        }
        //vector的最大值，dp不是前i个数的最长子序列
        return *max_element(std::begin(dp), std::end(dp)); 
    }
};

309 最佳买卖股票时机 含冷冻期

给一个价格数组，求买卖股票时机获取最大利润，股票卖出后，至少隔一天才可以再买。动态规划，定义两个数组变量own notown，分别表示今天有股票盈利的钱，以及今天没有股票盈利的钱。转移方程详见代码。
思路参考链接

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int len = prices.size();
        if(len < 2)
            return 0;
        vector<int> own(len, 0);
        vector<int> notOwn(len, 0);
        own[0] = -prices[0];
        own[1] = max(-prices[0], -prices[1]);

        for(int i = 1; i < len; i++){
            if(i > 1)
                own[i] = max(own[i-1], notOwn[i-2] - prices[i]);//至少前天卖出后，今天才能买
            notOwn[i] = max(notOwn[i-1], own[i-1] + prices[i]);
        }
        return max(own[len-1], notOwn[len-1]);
    }
};

332 零钱兑款

给定钱币面值数组，以及总钱数，给出所需最少钱币数量。第一次使用自己设计出了动态规划算法，定义dp数组，表示最少钱币数量，对所有面值进行遍历，dp[i] = min(dp[i], dp[i-coin] + 1)，求出dp[i]的最优解

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        if(amount == 0)
            return 0;
        vector<int> dp(amount + 1, -1);
        dp[0] = 0;
        for(int i = 0; i <= amount; i++){
            for(auto coin: coins){
                if(i < coin || dp[i-coin] == -1)
                    continue;
                if(dp[i] == -1)
                    dp[i] = dp[i-coin] + 1;
                else
                    dp[i] = min(dp[i], dp[i-coin] + 1);
            }
        }
        return dp[amount];
    }
};

337 打家劫舍Ⅲ

二叉树结构，连接的两个节点只能打劫一个，求最大值。属于二叉树的题目，用了一点动态规划的思想，如果打劫这个节点，那么子节点就不能要，反之如果不要这个节点，子节点可要可不要，取二者的最大值即可。递归实现的状态方程转移。

class Solution {
public:
    vector<int> robRec(TreeNode* root){ //vec0 is rob,veb1 not rob
        vector<int> robValue(2, 0);
        if(root == NULL)
            return robValue;
        
        vector<int> leftValue = robRec(root->left);
        vector<int> rightValue = robRec(root->right);
		//打劫当前节点
        robValue[0] = root->val + leftValue[1] + rightValue[1];
        //不打劫当前节点
        robValue[1] = max(leftValue[0], leftValue[1]) + max(rightValue[0], rightValue[1]);
        return robValue;
    }
    int rob(TreeNode* root) {
        vector<int> resValue = robRec(root);
        return max(resValue[0], resValue[1]);
    }
};

647 回文字符串

给一个字符串，返回其包含的子回文串的数量。动态规划思路，分三种情况：长度为1；长度为2且两字符相等;长度大于2，首尾字符相等，且除去首尾的字串也是回文串

class Solution {
public:
    int countSubstrings(string s) {
        int res = 0;
        int len = s.size();
        vector<vector<int>> dp(len, vector<int>(len, 0));
        for(int i = 0; i < s.size(); i++){
            for(int j = 0; j <= i; j++){
                if(i == j){ //长度为1
                    dp[i][j] = 1;
                    res++;
                }
                else if(i - j == 1 && s[i] == s[j]){ //长度为2,且字符相等
                    dp[i][j] = 1;
                    res++;
                }
                //长度大于2,字符相等，且j+1 至 i-1也是回文串
                else if(i - j > 1 && s[i] == s[j] && dp[i-1][j+1]){ 
                    dp[i][j] = 1;
                    res++;
                }
                else
                    continue;                

            }
        }
        return res;
    }
};

221最大正方形

给定一个二维01矩阵，求最大正方形的面积。自己想的思路，使用动态规划，求每个点为右下角的最大正方形，可以根据其左上角的点的情况确定。

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        int width = matrix[0].size();
        int height = matrix.size();

        //当前位置结束的宽边长度，高边长度，及正方形边长
        vector<vector<int>> widthLen(height, vector<int>(width, 0)); 
        vector<vector<int>> heightLen(height, vector<int>(width, 0));
        vector<vector<int>> dp(height, vector<int>(width, 0));
        int maxLen = 0;

        if(matrix[0][0] == '1'){
            widthLen[0][0] = heightLen[0][0] = dp[0][0] = 1;
            maxLen = 1;
        }
        for(int i = 1; i < width; i++){
            if(matrix[0][i] == '1'){
                widthLen[0][i] = widthLen[0][i-1] + 1;
                heightLen[0][i] = 1;
                dp[0][i] = 1;
                maxLen = 1;
            }
        }
        for(int i = 1; i < height; i++){
            if(matrix[i][0] == '1'){
                widthLen[i][0] = 1;
                heightLen[i][0] = heightLen[i-1][0] + 1;
                dp[i][0] = 1;
                maxLen = 1;
            }
        }
        for(int i = 1; i < height; i++){
            for(int j = 1; j < width; j++){
                if(matrix[i][j] == '0')
                    continue;
                widthLen[i][j] = widthLen[i][j-1] + 1;
                heightLen[i][j] = heightLen[i-1][j] + 1;
                int len = min(widthLen[i][j],  heightLen[i][j]);
                cout<<widthLen[i][j]<<heightLen[i][j]<<endl;
                //当前点为右下顶点的最大正方形边长，转移方程
                dp[i][j] = min(dp[i-1][j-1] + 1, len);
                maxLen = max(maxLen, dp[i][j]);
            }
        }
        return maxLen * maxLen;

    }
};

回溯、贪心

回溯算法是一种寻找解空间的搜索算法，而bfs、dfs等实在图或树结构的搜索算法，是一种穷举或枚举的算法。什么是解空间，比如求数组的全排列，可以用for循环实现，但是当如数很长的时候，需要使用很多层for循环，回溯算法是一种更合理的实现方法。回溯算法一般用递归dfs实现。

void backtrack(int i,int n,other parameters){
	if( i == n){
    	//get one answer
    	record answer;
		return;
	}
	//下面的意思是求解空间第i个位置上的下一个解
	for(next ans in position i of solution space){
		backtrack(i+1,n,other parameters);
	}
}

回溯通俗解释
回溯为什么用dfs实现呢，回溯的本质就是自己构建一个图，然后使用dfs遍历，还是以全排列为例，abc三个字母，长度未2排列情况，构建的图如下图所示，遍历的起始点就是第一行，列数就是长度2。如果再有其他要求，比如递增等，就是在dfs中对路径进行剪枝。

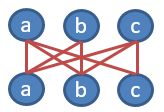
贪心算法是一种寻找局部最优解的思路，不一定是全局最优，因为是局部最优的非穷举方法，所以并非所有的问题都适用。例如最优支付问题，假如钱币面额为{200 100 20 10 5 1}，给定钱数，如何选择可以让支付钱币数量最少。贪心思路是尽量使用面额较大的钱币，如支付687，则需3张200，4张20，1张5，2张1，可以使得钱币数量最少。该题目中贪心算法好使的关键是，较大面额是较小面额的倍数关系，1张较大面额肯定可以被多张较小面额替代。假设增加7元面额呢，如我们要支付14元，显然贪心算法得不到最优解，这种情况，可能需要动态规划或回溯来解决了。

47 全排列

给一个vector数组，给出全排列情况，数组中有重复元素，全排列不能含重复项。全排列是回溯典型使用场景，相比最简单的全排列，这里出现列重复元素，因此要剪支回退。

class Solution {
public:
    vector<vector<int>> res;
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        vector<bool> used(nums.size(), false);
        vector<int> path;
        sort(nums.begin(), nums.end());
        backTrack(0, nums, used, path);
        return res;
    }
    //DFS实现的回溯
    void backTrack(int index, vector<int>& nums, vector<bool>& used, vector<int>& path) {
        if(index == nums.size()){
            res.push_back(path);
            return;
        }

        for(int i = 0; i < nums.size(); i++) {
            if(used[i] == true)
                continue;
            //剪支条件，如果和上一个数相同，并且上一个数被回退过。保证同一层级该数出现只出现一次
            //另一种解释：如aaa连续a的情况，如果第一个a没有被用过，先去用第一个a，针对这三个a，没有全排列
            if(i > 0 && nums[i] == nums[i-1] && used[i-1] == false)
                continue;
            used[i] = true;
            path.push_back(nums[i]);
            backTrack(index+1, nums, used, path);
            used[i] = false;
            path.pop_back();  //删除队尾元素
        }
    }
};

39 组合总和

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合
输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
牵涉到组合，想到用回溯。这个题目中元素可以重复使用，因此无需定义used数组，需要注意的是，for循环中，仍需要剪枝
if(path.size() > 0 && num < path[path.size()-1])，如果当前数小于path的最后一个跳过，防止已经有了【2，2，3】答案后，dfs又出现【2 3 2】或【3，2，2】的答案。自己实现的代码。

class Solution {
public:
    void backtrace(vector<int>& candidates, int target, vector<vector<int>>& res, vector<int>& path, int sumNum) {
        if(sumNum == target){
            res.push_back(path);
        }
        else if(sumNum > target)
            return;
        else {
            for(auto num:candidates){
                if(path.size() > 0 && num < path[path.size()-1])
                    continue;
                vector<int> temp = path;
                temp.push_back(num);
                backtrace(candidates, target, res, temp, sumNum + num);
            }
        }
    }
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector<vector<int>> res;
        int sumNum = 0;
        vector<int> path;
        backtrace(candidates, target, res, path, sumNum);
        return res;
    }
};

大礼包

买东西的最少价格，有需要各类物品总数，单价，还有大礼包价格。回溯类型的题目，自己想的思路，对大礼包进行回溯的全排列，超出商品数目就退出，不足的用单个补齐，提交后超时了，逻辑是对的。
输入：price = [2,5], special = [[3,0,5],[1,2,10]], needs = [3,2]
输出：14
解释：有 A 和 B 两种物品，价格分别为 ¥2 和 ¥5 。
大礼包 1 ，你可以以 ¥5 的价格购买 3A 和 0B 。
大礼包 2 ，你可以以 ¥10 的价格购买 1A 和 2B 。
需要购买 3 个 A 和 2 个 B ， 所以付 ¥10 购买 1A 和 2B（大礼包 2），以及 ¥4 购买 2A 。

class Solution {
public:
    int minPrice = -1;
    void backTrace(vector<int>& price, vector<vector<int>>& special, vector<int>& needs, int allPrice) {        
        int leftPrice = 0;
        for(int i = 0; i < needs.size(); i++) {
            if(needs[i] < 0)
                return;
            leftPrice += needs[i] * price[i];
            //leftNeeds += needs[i];
        }
        int temp_all = allPrice + leftPrice;
        if(minPrice == -1 || minPrice > temp_all)
         minPrice = temp_all;
         //cout<
        
        for(int i = 0; i < special.size(); i++) {
            vector<int> tempNeeds = needs;
            for(int j = 0; j < special[i].size() - 1; j ++) {
                tempNeeds[j] -= special[i][j];
                
            }
            backTrace(price, special, tempNeeds, allPrice + special[i][special[i].size() - 1]);
        }
    }
    int shoppingOffers(vector<int>& price, vector<vector<int>>& special, vector<int>& needs) {
        int allPrice = 0;
        backTrace(price, special, needs, 0);
        int ret = minPrice;
        return ret;

    }
};

二叉树

94数的中序遍历

前序、中序或后续其实就是那三句话的顺序，此处使用递归实现的遍历

class Solution {
public:
    void traversalTree(TreeNode* root, vector<int>& res){
        if(root == NULL){
            return;
        }
        traversalTree(root->left, res);
        res.push_back(root->val);
        traversalTree(root->right, res);
    }
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        traversalTree(root, res);
        return res;
    }
};

114二叉树展开为链表

程序只有一个TreeNode*参数，将普通的二叉树，按照前序遍历的顺序放到链表中，这里的链表用了TreeNode节点的right分支实现。
这个程序是自己实现调试完成的，总体思路是递归实现的前序遍历框架，递归函数加了一个链表指针参数，链表当前状态指针（最后一个节点），这个参数用了指针的引用形式，有助于理解下指针和引用的应用。另外下面程序里有句注释还是要理解下！

class Solution {
public:
    void qianxubianli(TreeNode* root, TreeNode* &tempNode){
        if(root == NULL){
            return;
        }
        //cout<val<
        tempNode->right = root;
        tempNode->left = NULL;
        tempNode = root;
        
        //为什么加这一句，此时tempNode=root，传到左分支递归调用时，会被改变
        TreeNode* r_temp = root->right;
        qianxubianli(root->left, tempNode);
        qianxubianli(r_temp, tempNode);
    }
    void flatten(TreeNode* root) {
        TreeNode *first = new TreeNode;
        qianxubianli(root, first);
        
    }
};

102二叉树的层序遍历

要求将结果存储到一个二维vector中返回，我自己是按照前序遍历实现的，将结果push到vector特定位置，应该还有更好的办法，待更新。。。。。。

class Solution {
public:
    void qianxubianli(TreeNode* root, vector<vector<int>>& res, int depth){
        if(root == NULL){
            return;
        }
        if(res.size() < depth + 1){
            vector<int> temp;
            res.push_back(temp);
        }
        res[depth].push_back(root->val);
        qianxubianli(root->left, res, depth+1);
        qianxubianli(root->right, res, depth+1);
    }
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> res;
        qianxubianli(root, res, 0);
        return res;      

    }
};

层序遍历正常都应该想到BFS，这里不同于正常的层遍历，要把他们放到指定的vector中，一种思路把深度和节点作为一个元组一起送入queue，另一种思路参考别人的，比较巧妙，控制从queue中取出的次数，一次取出一个层的数据，看注释处！

class Solution {
public:   
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> res;
        if(!root)
            return res;
        queue<TreeNode*> q;
        q.push(root);
        while(!q.empty()){
            int len = q.size();
            vector<int> currentLayer;
            //不同于普通bfs，这里加了一层循环，每次取出一层的数据
            for(int i = 0; i < len; i++){
                TreeNode* current = q.front();
                q.pop();
                currentLayer.push_back(current->val);
                if(current->left){
                    q.push(current->left);
                }
                if(current->right){
                    q.push(current->right);
                }                
            }
            res.push_back(currentLayer);            
        }
        return res;  
    }
};

105从前序与中序遍历序列构造二叉树

给了一个二叉树的前序序列和中序遍历的序列，要求构造出完整二叉树。思路是要用递归实现，前序遍历的第一个数就是root节点，在中序遍历序列中找到这个数，那么在在中序序列中，该数左边就是左分支，右边就是右分支。以此思路递归，关键的是如何确定前序序列的左右分支，是根据中序序列的长度确定的，前序root节点后，index个数是左分支，再之后是右分支
参考解体思路

class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if(preorder.empty() && inorder.empty())
            return NULL;
        TreeNode* root = new TreeNode;
        root->val = preorder[0];

        vector<int>::iterator iter = find(inorder.begin(), inorder.end(), preorder[0]);
        int index = distance(inorder.begin(), iter);
    
        vector<int> inorder_l(inorder.begin(), inorder.begin() + index);
        vector<int> inorder_r(inorder.begin() + index + 1, inorder.end());
        vector<int> preorder_l(preorder.begin() + 1, preorder.begin() + 1 + index);
        vector<int> preorder_r(preorder.begin() + 1 + index, preorder.end());

        root->left = buildTree(preorder_l, inorder_l);
        root->right = buildTree(preorder_r, inorder_r);
        return root;
    }
};

226反转二叉树

题目简单，完全自己实现的，递归思路，由上至下的反转，试了下由下至上也是可以的，调换下语句顺序即可。

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(root == NULL){
            return root;
        }
        swap(root->left, root->right);
        root->left = invertTree(root->left);
        root->right = invertTree(root->right);        
        return root;
    }
};

96不同的二叉搜索树

给定一个整数 n，求以 1 … n 为节点组成的二叉搜索树有多少种。用动态规划比较容易
参考的别人的方法实现的

class Solution {
    public int numTrees(int n) {
        //dp[i]表示有i个结点时二叉树有多少种可能
        int[] dp = new int[n + 1];
        //初始化
        dp[0] = 1;
        dp[1] = 1;
        
        //因为计算dp[n]需要知道dp[0]--->dp[n-1]。所以第一层循环是为了求dp[i]
        for (int i = 2; i <= n; i++) {
            //当有i个结点时，左子树的节点个数可以为0-->i-1个。剩下的是右子树。
            for (int j = 0; j < i; j++) {
                dp[i] += dp[j] * dp[i - j - 1];
            }
        }
        return dp[n];//n个数，就返回dp[n],非n-1
    }
}

98验证二叉搜索树

给定一个二叉树，判断其是否是一个有效的二叉搜索树。
一开始，使用简单的递归，比较当前节点和左右分支的大小关系实现的，结果只有部分用例通过，原因是没有搞清楚二叉搜索树的概念，当前节点不是比右节点大就可以，并且要大于右节点的所有子节点！

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        if(root == NULL){
            return true;
        }
        if(root->left){
            if(root->val <= root->left->val){
                return false;
            }
            if(!isValidBST(root->left)){
                return false;
            }
        }

        if(root->right){
            if(root->val >= root->right->val){
                return false;
            }
            if(!isValidBST(root->right)){
                return false;
            }
        }
        
    return true;
    }
};

于是，换了一种思路，用中序遍历实现，放到一个vector里，比较当前插入的数字，比上一个数字大就行了

class Solution {
public:
    bool zhongxubianli(TreeNode* root, vector<int>& vec){
        if(root == NULL){
            return true;
        }
        if(!zhongxubianli(root->left, vec))
            return false;    //一定要返回false，不能只递归调用而不使用其返回值！
        vec.push_back(root->val);
        cout<<root->val<<endl;
        int len = vec.size();
        if(len > 1 && vec[len-1] <= vec[len-2]){
            return false;
        }
        if(!zhongxubianli(root->right, vec))
            return false;
        return true;
    }
    bool isValidBST(TreeNode* root) {
        vector<int> vec;
        return zhongxubianli(root, vec);
    }
};

538 把二叉搜索树转换为累加树

右节点加父节点，当前节点再加右节点，左节点再加当前节点，可以用二叉树的中序遍历实现，右中左的顺序

class Solution {
public:
    TreeNode* convertBST(TreeNode* root) {
        midOrder(root, 0);
        return root;        
    }
    int midOrder(TreeNode* root, int fartherVal){
        if(root == NULL)
            return fartherVal;
        int rightSum = midOrder(root->right, fartherVal);
        root->val = root->val + rightSum;
        int leftSum = midOrder(root->left, root->val);
        return leftSum;
    }    
};

617 合并二叉树

合并两个二叉树，相同位置的数字相加，一个没有的取另一个。遍历二叉树即可，比较简单（为了不额为申请内存，改变并返回了root1）

class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if(root1 == NULL)
            return root2;
        if(root2 == NULL)
            return root1;
        root1->val += root2->val;
        root1->left = mergeTrees(root1->left, root2->left);
        root1->right = mergeTrees(root1->right, root2->right);
        return root1;
    }
};

108 将有序数组转换为二叉搜索树

要求二叉搜索数是平衡的，因此需要将数组的中位数作为跟节点，以此向下递归

class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        int len = nums.size();
        if(0 == len)
            return NULL;
        int mid = len / 2;
        TreeNode* node = new TreeNode(nums[mid]);
        
        //vector 截取
        vector<int>::iterator first1 = nums.begin();
        vector<int>::iterator last1 = nums.begin() + mid;
        vector<int> leftNums(first1, last1);
        node->left = sortedArrayToBST(leftNums);
        

        vector<int>::iterator first2 = nums.begin() + mid + 1;
        vector<int>::iterator last2 = nums.end();
        vector<int> rightNums(first2, last2);
        node->right = sortedArrayToBST(rightNums);

        return node;
    }
};

链表

c++中链表

141环形链表

判断链表是否有环，快慢指针，自己实现的

class Solution {
public:
    bool hasCycle(ListNode *head) {
        if(head == NULL || head->next == NULL)
            return false;
        ListNode* p = head;
        ListNode* n = head;
        while(n && n->next){ //前面的n要加上，遍历过程中n或n->net都有可能先为NULL
            n = n->next->next;
            p = p->next;
            if(p == n)
                return true;
        }
        return false;        
    }
};

142环形链表Ⅱ

判断链表是否有环，并返回第一个入环的节点，否则返回null。思路首先想到的还是利用快慢指针判断是否有环，怎么找到第一个入环的节点呢，简单的办法是把节点地址存入哈希，重复的可以比较出来，另一种比较简单的思路参考别人的，快慢指针同时到达某个节点后，这个节点正好存在一个路程的2被关系，详见下面的注释

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if(head == NULL || head->next == NULL)
            return NULL;
        ListNode* p = head;
        ListNode* n = head;
        while(n && n->next){ //前面的n要加上，遍历过程中n或n->net都有可能先为NULL
            n = n->next->next;
            p = p->next;
            if(p == n){
                //如果顺次走，第二次到达p的路程是第一次到达p路程的两倍
                //如果分别从head和p出发，那么下次还会同时达到p，也会同时到达第一个入环节点
                while(head != p){
                    p = p->next;
                    head = head->next;
                }
                return p;
            }                
        }
        return NULL;          
    }
};

234回文链表

判断一个链表是否会问链表，要求时间复杂度O(N)，空间复杂度O(1)，借鉴别人的思路，快慢指针，找到中间位置，然后对中间位置后的链表进行逆序，最后逐个对比，自己写的代码

class Solution {
public:
    bool isPalindrome(ListNode* head) {
        if(head == NULL || head ->next == NULL)
            return true;
        ListNode *slow = head, *fast = head;
        while(fast && fast->next){
            slow = slow->next;
            fast = fast->next->next;
        }
        //从slow开始逆序
        ListNode * p = NULL, * n;
        while(slow){
            n = slow->next;
            slow->next = p;
            p = slow;
            slow = n;
        }
        //逐个比较，可不用考虑奇偶情况，p是逆序后的链表头
        while(p){
            if(p->val != head->val)
                return false;
            p = p->next;
            head = head->next;
        }
        return true;
    }
};

160相交链表

判断两个链表是否存在交点，存在返回交点地址，否则返回NULL。直观思路遍历一个链表，将地址存入哈希，遍历第二个链表，逐个判断是否存在地址相同节点。但是，题目要求空间复杂度O(1)，即存储空间不能和链表长度相关。
参考别人的思路，简单分两步
1、各遍历一次链表，求两者的长度差；
2、长的链表先走差值个节点，然后两个链表同步next并校验next是否相同，相同即表示找到了交点，否则最终为null；
代码待补充！！

栈

先进先出的数据结构，处理括号问题是典型应用

394 字符串解码

给定s = “3[a]2[bc]” 中括号里的a被重复3词，解码后返回"aaabcbc"。因为有括号操作，一般使用栈。参考别人思路，使用了两个栈，分别存储数字和字符串，细节部分有点抽象，结合注释好好理解，自己想不出来。

class Solution {
public:
    string decodeString(string s) {
        string resStr;
        stack<int> nums;
        stack<string> chars;
        int num = 0;
        string subStr = "";
        for(auto c: s){
            if((c>='a' && c <='z')||(c>='A' && c <='Z'))
                subStr += c;
            else if(c >= '0' && c <= '9')
                num = num * 10 + c - '0'; //处理连续数字
            else if('[' == c){
                nums.push(num);
                num = 0;
                chars.push(subStr);//前面出现的字符先推入栈
                subStr = "";
            }
            else {
                int k = nums.top();
                nums.pop();
                for(int i = 0; i < k; i++)
                    chars.top() += subStr; //实际就是重复k此后，又加上了栈顶元素
                subStr = chars.top(); //subStr等于栈顶的元素加上重复序列
                chars.pop();
            }
        }
        return subStr;
    }
};

739 每日温度

给定每日温度列表，返回温度升高的天数，即后面低几天会比今天温度高，输入输出如下。暴力方法简单，O（N×N)超时。看别人的思路，可以维护一个存储下标的单调栈，从栈底到栈顶的下标对应的温度列表中的温度依次递减。如果一个下标在单调栈里，则表示尚未找到下一次温度更高的下标
用最小栈方法，所谓最小栈，就是栈顶元素最小，向下递增，如果要插入的新元素，比栈顶大，不能直接插入，要把小于当前值的数统统处理掉。思路还是有点难的。
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]

class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& temperatures) {
        int len = temperatures.size();
        vector<int> riseDays(len, 0);
        stack<int> s;
        for(int i = 0; i < len; i++){
            //把栈顶小于当前值的处理掉
            while(!s.empty() && temperatures[i] > temperatures[s.top()]){
                int t = s.top();
                s.pop();
                riseDays[t] = i - t; //i就是升温的那一天，计算差值即可
            }
            s.push(i); //推入当前值
        }
        return riseDays;
    }
};

排序或查找算法

常见的排序算法包括冒泡、快排、归并排序、栈排序等，详细可参考我的另一篇博客《排序算法介绍》

148排序链表（排序+链表）

将一个无序链表进行排序，一开始想到的思路是顺次插入，插入的时候按照顺序找到特定位置，程序调通了，但是最终超时，要求是O(nlogn)，我的可能是O(nn)

class Solution {
public:
    ListNode* insertList(ListNode* head, ListNode* p){
        if(p->val <= head->val){
            p->next = head;
            return p;
        }
        else{
            ListNode* temp = head;
            while(temp != NULL){
                if(temp->next == NULL){
                    temp->next = p;
                    p->next = NULL;
                    break;
                }
                else{
                    if(temp->val <= p->val && p->val <= temp->next->val){
                        p->next = temp->next;
                        temp->next = p;
                        break;
                    }
                }
                temp = temp->next;
            }
            return head;
        }
    }
    ListNode* sortList(ListNode* head) {
        if(head == NULL || head->next == NULL)
            return head;
        ListNode* p = head->next;
        head->next = NULL;  //子链表
        ListNode* temp;
        while(p){
            temp = p->next;//p不会被改变，但是p-next可能会被改变
            head = insertList(head, p);
            p = temp;
        }
        return head;
    }
};

参考别人的思路，使用归并排序或快排，自己按照归并排序的思路，最终调通。递归实现，递归思路参考上述博客中的递归排序套路，花了一下午时间才调通，值得好好对比研究

class Solution {
public:
    ListNode* mergeList(ListNode* p1, ListNode* p2){
        if(p1 == NULL)
            return p2;
        if(p2 == NULL)
            return p1;
        ListNode* head, *p;
        if(p1->val < p2->val){
            head = p1;
            p1 = p1->next;
        }
        else{
            head = p2;
            p2 = p2->next;
        }
        p = head;
        while(p1 && p2){
            if(p1->val < p2->val){
                p->next = p1;
                p1 = p1->next;
            }
            else{
                p->next = p2;
                p2 = p2->next;
            }
            p = p->next;
        }
        //p->next = NULL; //链表end
        if(p1)
            p->next = p1;
        if(p2)
            p->next = p2;
        return head;
    }
    ListNode* sortList(ListNode* head) {
        if(head == NULL || head->next == NULL)
            return head;
        ListNode* slow = head, *fast = head, *middle;
        while(fast && fast->next){
            middle = slow;
            slow = slow->next;
            fast = fast->next->next;
        }
        middle->next = NULL;
        ListNode* p1 = sortList(head);
        ListNode* p2 = sortList(slow);
        head = mergeList(p1, p2);
        return head;
    }
};

215数组中的第K个最大元素

返回数组中第K个最大元素，使用快排思路（参考我的”排序算法介绍“博客）。快排使用分治思想，不断切分数组，切分函数返回的index就是数组中第index个大或小的树，利用这一思想，假设K落在index的右边，接下来只对，右边的子数组进行递归就行，代码如下（相对快排，只修改了quickSort函数，partition没变）

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        quickSort(nums, 0, nums.size() - 1, k);
        return nums[nums.size() - k];
    }
private:
    int partition(vector<int> &num, int low, int high)
    {
        int point = num[low]; //第一个数作为基准值
        while (low < high)
        {

            while (low < high && num[high] >= point) // 右侧大于等于point不处理
            {
                high--;
            }
            swap(num[low], num[high]); // 将右侧边界的小于point的点与左侧边界交换
            while (low < high && num[low] <= point)
            {
                low++;
            }
            swap(num[low], num[high]);
        }
        return low;
    }

    void quickSort(vector<int> &num, int low, int high, int k)
    {

        if (low >= high)
            return;
        int index = partition(num, low, high);
        if(index == num.size() - k){
            return;
        }
        else if(index < num.size() - k){
            quickSort(num, index + 1, high, k);
        }
        else{
            quickSort(num, low, index - 1, k);
        }        
    }
};

240搜索二维矩阵Ⅱ

在有序二维矩阵中查找特定数字，不是排序算法。矩阵的规律有点特别，参考了别人的思路，思路难，实现容易。从右上角开始遍历，所有比当前数小的数字都在当前位置左边，所有比当前数大的都在当前位置下面，所以以此规律进行向左或向下的查找。

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int w = matrix[0].size();
        int h = matrix.size();

        int i = 0, j = w -1;
        while(i < h && j >= 0){
            if(matrix[i][j] < target)
                i++;
            else if(matrix[i][j] > target)
                j--;
            else
                return true;
        }
        return false;        
    }
};

287寻找重复数

寻找一个数组中重复的数字，只有一个重复的，且数字大小在1和数组长度之间。除了排序，没想出好的思路。参考别人的思路，二分查找和链表找环法。二分查找实现的，遍历数组，找介于left到mid之间的数字，如果数字个数大于left-mid，说明重复的数字介于他们之间，不断二分查找

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int l = 1, r = nums.size() - 1;
        int cnt = 0, mid;

        while(l < r){
            mid = (l + r) >> 1;

            for(int i = 0; i < nums.size(); i++){
                if(nums[i] >= l && nums[i] <= mid)
                    cnt++;
            }
            if(cnt > mid - l + 1) //重复的数在前半段
                r = mid;
            else
                l = mid + 1;
            cnt = 0;
        }
        return r;
    }
};

参考思路

哈希算法

c++中hash算法一般使用stl库的map实现，map和python的dick非常相似。

128最长连续序列

输入：nums = [100,4,200,1,3,2]
输出：4
解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

题目如上，比较容易理解。要求算法复杂度是log(n)，因此不能用排序。思路是使用哈希实现，粗暴实现比较简单，把所有数字插入到hash中，重复的不必重复插入，遍历统计以该数字为起始点的最长连续序列，找出最大length即可。
暴力方法显然超时，比较简单的方法是，比如我们有一个连续序列1 2 3，我们只要保证两端长度正确即可，即map[1] map[3]的长度都是3，map[2]有数就行，可以不准。这样当我们插入4的时候，先看看3和5的情况，3已有，并且长度为3，那么我们可以更新map[1] map[4]的数字

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        int max_len = 0;
        map<int ,int> len_hash;
        for(auto num:nums){
            if(len_hash.count(num)) continue;
            int left = len_hash.count(num - 1)? len_hash[num-1]:0;
            int right = len_hash.count(num + 1)? len_hash[num+1]:0;
            int len = left + right + 1;
            max_len = max(len, max_len);
            len_hash[num] = len;
            len_hash[num - left] = len;
            len_hash[num + right] = len;
        }
        return max_len;
    }
};

347 前K个高频元素

统计数组出现次数前K多的元素，自己想的普通思路，哈希统计每个元素出现的次数，再把哈希倒过来出现次数为n的元素，把n组成数组，然后排序，找对对那个的前K个元素。里面用到了sort函数，可以对vector或数组进行排序，另外当类的成员函数当作函数指针时，需设置为static成员函数，程序注释说明了原因

class Solution {
public:
    vector<int> topKFrequent(vector<int>& nums, int k) {
        map<int, int> hashFrequence;
        for(auto num: nums){
            if(hashFrequence.count(num))
                hashFrequence[num] += 1;
            else
                hashFrequence[num] = 1;
        }

        map<int, vector<int>> freqNum;
        vector<int> freqs;
        for(map<int, int>::iterator iter = hashFrequence.begin(); iter != hashFrequence.end(); iter++){
            if(freqNum.count(iter->second)){
                freqNum[iter->second].push_back(iter->first);
            }
            else{
                vector<int> tempNums(1, iter->first);
                freqNum[iter->second] = tempNums;
                freqs.push_back(iter->second);  //频次只插入一次
            }                
        }

        sort(freqs.begin(), freqs.end(), cmp);
        vector<int> topKFreq;

        int index = 0;
        for(auto i: freqs){
            for(auto j: freqNum[i]){
                topKFreq.push_back(j);
                index++;
                if(index == k)
                    return topKFreq;
            }
        
        }
        return topKFreq;

    }
private:
/*问题的原因其实就是函数参数不匹配的问题。因为我们普通的成员函数都有一个隐含的this指针，表面上看我们的谓词函数com（）只有两个参数，但实际上它有三个参数，
而我们调用sort（）排序函数的时候只需要用到两个参数进行比较，所以就出现了形参与实参不匹配的情况（函数有三个形参，但是只输入了两个实参）
*/
    static bool cmp(int x, int y){
        return x > y;
    }
};

36 有效的数独

给一个9×9的方格，每个格子可能填列0-9的数字，没填的用’.'表示，要求每行每列或者每个临近3×3的大格子不能有重复的数字，明显使用哈西，实现也比较简单直观

class Solution {
public:
    bool isValidSudoku(vector<vector<char>>& board) {
        map<char, int> rowMap[9], colMap[9], gridMap[9];
        for(int i = 0; i < 9; i++){
            for(int j = 0; j < 9; j++){
                if('.' == board[i][j]) //未填写数字的就直接跳过
                    continue;
                if(1 == rowMap[i].count(board[i][j]))
                    return false;
                else
                    rowMap[i][board[i][j]] = 1;

                if(1 == colMap[j].count(board[i][j]))
                    return false;
                else
                    colMap[j][board[i][j]] = 1;

                int gridIndex = i/3*3 + j/3;
                if(1 == gridMap[gridIndex].count(board[i][j]))
                    return false;
                else
                    gridMap[gridIndex][board[i][j]] = 1;

            }
        }
        return true;
    }
};
 

双指针

快慢指针和左右指针都属于双指针，判断链表是否有环用快慢指针，左右指针简单点解释，比如给定一个有序数组，以及一个target数值，返回数组中加起来等于target的两个数的索引值，使用左右双指针比较容易解决，只要数组有序，就应该想到双指针技巧

1 两数之和

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
例如：
输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1]
思路：暴力算法或双指针，排序后从两侧向内移动，找到两个相加为target的数。也可以用哈希，一次for循环解决
双指针代码（别人的）
以该题为例，为什么双指针法奏效呢，假设两个目标索引是m和n（m小 n大），m和任何大于n的索引，和一定是大于目标的，n和任何小于m的索引，和一定是小于目标的，因此双指针发一定不会错过答案

class Solution {
public:
    vector<int> twoSum(vector<int>& numbers, int target) {
        vector<int> a(2,-1);
        int i=0,j=numbers.size()-1;
        while(i<j)
        {
            if(numbers[i]+numbers[j]==target)
            {
                a[0]=i+1;
                a[1]=j+1;
                return a;
            }
            else if(numbers[i]+numbers[j]>target)
            {
                j--;
            }
            else
            {
                i++;
            }
        }
        return a;
    }       
};

哈希实现代码（别人的）

class Solution {
public:
    vector<int> twoSum(vector<int>& numbers, int target) {
        map<int,int> a;
        vector<int> result(2,-1);
        for(int i=0;i<numbers.size();i++)
        {
            if(a.count(target-numbers[i])>0)
            {
                result[0]=i+1;
                result[1]=a[target-numbers[i]]+1;
                break;
            }
            a[numbers[i]]=i;
        }
        sort(result.begin(),result.end());
        return result;
    }
};

15 三数之和

待补充，在两数之和的基础上，固定第一个数，后两个数双指针移动

4寻找两个正序数组的中位数

两个数组均是有序数组，寻找他们合并数组的中位数。有序数组应该想到用双指针，根据两数组长度之和，计算中位数的index，然后使用双指针，在两个数组中移动寻找。思路比较明确，但是有些细节需要注意，比如长度的奇偶情况，以及双指针的一个移动到数组末尾后等，自己实现的程序如下，可能代码有些冗余，时间复杂度还可以

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int len = nums1.size() + nums2.size();
        if(len == 1)
            return nums1.size()?nums1[0]:nums2[0];
        int index = 0, i = 0, j = 0;
        vector<int> result;
        while(index <= (len + 1) / 2){  //这里len+1，循环里len-1，巧妙处理奇偶情况
            if(i >= nums1.size()){  //其中一个数组移动到末尾
                if(index >= (len-1) / 2)
                    result.push_back(nums2[j]);
                j++;
                index++;
                continue;
            }
            if(j >= nums2.size()){
                if(index >= (len-1) / 2)
                    result.push_back(nums1[i]);
                i++;
                index++;
                continue;
            }

             if(nums1[i] < nums2[j]){
                if(index >= (len-1) / 2)
                    result.push_back(nums1[i]);
                i++;
            }                
            else{
                if(index >= (len-1) / 2)
                    result.push_back(nums2[j]);
                j++;
            }          
            index++;
        }
        for(auto i: result){
            cout<<"res"<<i<<endl;
        }
     
        if(len % 2)
            return result[0];
        else
            return double(result[0]+result[1])/2;          
    }
};

并查集

一种集合合并的算法，如求多少联通区域等问题。代码参考下面的130题目。
原理介绍

130 被围绕的区域

给一个二维矩阵，由‘x’和‘0’组成，如果一个0的联通区域被x所包围，那么该区域的0全部改写称x，并返回新的矩阵。关于联通区域的问题，想到并查集（该题目bfs或dfs也可以），将所有的0区域放入并查集找联通区域，合并后可以分成两种，一种是临近边界的，一种是内部的，如果不边界的，那么都是被包围的，置为x就可以了

class DisjSet
{
private:
    vector<int> parent;    //父节点
    vector<int> rank;    //树的高度

public:
    DisjSet(int max_size) : parent(vector<int>(max_size)), rank(vector<int>(max_size))
    {
        // 初始化每一个元素的根节点都为自身
        for (int i = 0; i < max_size; ++i) {
            parent[i] = i;     //每个结点的上级都是自己
            rank[i] = 1;    //每个结点构成的树的高度为1
        }
    }
    /*
    int find_parent(int x)     //查找结点x的根结点
    {
        if(parent[x] == x){        //递归出口：x的上级为x本身，即x为根结点
            return x;      
        }
        return find_parent(parent[x]);    //递归查找
    }
    */
    //改进查找算法：完成路径压缩，将x的上级直接变为根结点，那么树的高度就会大大降低
    int find_parent(int x)     //查找结点x的根结点
    {
        if(parent[x] == x){        //递归出口：x的上级为x本身，即x为根结点
            return x;      
        }
        return parent[x] = find_parent(parent[x]);   //递归查找  此代码相当于 先找到根结点rootx，然后parent[x]=rootx
    }
    
    
    bool is_same(int x, int y)      //判断两个结点是否连通
    {
        return find_parent(x) == find_parent(y);  //判断两个结点的根结点（亦称代表元）是否相同
    }
    
    void unite(int x,int y)
    {
        int rootx, rooty;
        rootx = find_parent(x);
        rooty = find_parent(y);
        if(rootx == rooty){
            return ;
        }
        if(rank[rootx] > rank[rooty]){
            parent[rooty] = rootx;         //令y的根结点的上级为rootx
        }
        else{
            if(rank[rootx] == rank[rooty]){
                rank[rooty]++;
            }
            parent[rootx] = rooty;
        }
    }
};

class Solution {
public:
    void solve(vector<vector<char>>& board) {
        int row = board.size();
        int col = board[0].size();
        vector<vector<int>> nieghborCor = {{-1,0}, {1,0}, {0,-1}, {0,1}};
        DisjSet disjset(row * col + 1);    //+1,多初始化一个存储边界联通区的o
        for(int i = 0; i < row; i++) {
            for(int j = 0; j < col; j++) {
                if(board[i][j] != 'O')
                    continue;
                if(i == 0 || i == row - 1 || j == 0 || j == col - 1)  //边界区域的o
                    disjset.unite(i * col + j, row * col);
                else {
                    for(int k = 0; k < nieghborCor.size(); k++) {  //相邻坐标的o连接到一起
                        int x = i + nieghborCor[k][0];
                        int y = j + nieghborCor[k][1];
                        if(board[x][y] == 'O')
                            disjset.unite(i * col + j, x * col + y);                    
                    } 
                }                  
            }
        }

        for(int i = 0; i < row; i++) {
            for(int j = 0; j < col; j++) {
                if(board[i][j]  == 'O' && !disjset.is_same(i * col + j, row * col))
                    board[i][j] = 'X';
            }
        }

    }
};

其他

数组操作、。。。。

121买卖股票的最佳时机

输入：[7,1,5,3,6,4]
输出：5 获得最大利润是5，价格是1的时候买，6的时候卖掉
直观思路，使用类似冒泡的操作，求每天买入能够获得的最大收益即可
更好的办法，是一次循环完成，更新最小价格，和最大利润，为什么是最小价格而不是最大价格，这是由于必须是当前的大数减去之前小的数，才是股票收益！

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if(prices.size() == 0)
            return 0;
        int max_profit = 0;
        int min_price = prices[0];
        for(auto i:prices){
            if(min_price > i)
                min_price = i;
            max_profit = max(max_profit, i - min_price);
        }
        return max_profit;
    }
};

152乘积最大的子数组

给你一个整数数组 nums ，请你找出数组中乘积最大的连续子数组，返回该乘积。看到这道题没有很好的思路，暴力方法运算量太大肯定不可取。可能可以用动态规划实现，但是不知道怎么解。看到别人的思路O(n)的复杂度，循环一次，记录局部最大乘积，最小乘积，当遇到负数的时候，局部最大和最小交换

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int max_p = 1, min_p = 1, result = nums[0];
        for(auto num:nums){
            //遇到负数时，局部最小值和局部最大值交换
            if(num < 0){
                int temp = min_p;
                min_p = max_p;
                max_p = temp;
            }
            max_p = max(max_p*num, num);
            min_p = min(min_p*num, num);
            result = max(result, max_p);

        }
        return result;
    }
};

238除自身以外数组的乘积

一般思路都是计算总乘积，除以当前数字即可，题目不允许用除法。那么就分别计算每个数左右两边数的乘积，计算这两个值，可以复用前面的结果

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int len = nums.size();
        vector<int> leftProduct(len, 1);
        vector<int> rightProduct(len, 1);
        vector<int> product(len, 1);

        for(int i = 1; i < len; i++){
            leftProduct[i] = leftProduct[i-1] * nums[i-1];
        }
        for(int i = len-2; i >= 0; i--){
            rightProduct[i] = rightProduct[i+1] * nums[i+1];
        }

        for(int i = 0; i < len; i++){
            product[i] = leftProduct[i] * rightProduct[i];
        }
        return product;
    }
};

338 比特位计数

给定一个数N，计算从0到N的所有数的二进制1的个数，返回数组。粗暴的方法是分别移位统计计算，看别人的思路，有一定规律如前8个数【0 1 1 2 1 2 3 4】，resBits[i] = resBits[i-t] + 1，当然t的长度是变化的。

class Solution {
public:
    vector<int> countBits(int n) {
        vector<int> resBits(n + 1);
        resBits[0] = 0;
        int t = 1;

        for(int i = 1; i <= n; i++){
            if(i == 2 * t)//到2 4 8 16数字时，t乘2
                t *= 2;
            resBits[i] = resBits[i-t] + 1;     
        }
        return resBits;
    }
};

29两数相除

计算两个数的商，不能用乘除以及取模运算，参考别人的思路，使用移位的办法，任何一个数，包括商，都可以表示为2的31次方+2的30次方……+2的0次方，非常巧妙

class Solution {
public:
    int divide(int dividend, int divisor) {
        if(dividend == INT_MIN && divisor == -1)
            return INT_MAX;
        int sign = dividend ^ divisor;
        long dvd = abs(dividend);
        long dvs = abs(divisor);
        long ans = 0;
        //累加结果，2的31次方，2的30次方……
        for(int i = 31; i >= 0; i--) {
            if((dvd>>i) >= dvs){
                dvd -= dvs<<i;
                ans += 1<<i;
            }
        }
        if(sign < 0)
            ans = -ans;
        return ans;
    }
};

136只出现一次的数字（位运算）

返回数组中只出现一次的数字，只有一个，其他数字均出现两次或两次以上。要求一次循环，不额外使用空间，所以哈希不能用了。使用异或实现的！

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int result = nums[0];
        for(vector<int>::iterator iter = nums.begin() + 1; iter != nums.end(); iter++){
            result ^= *iter;
        }
        return result;
    }
};

283移动零

把数组的所有零移动到最后，其他数字相对位置不变。题目很简单，自己想的思路，遍历一次，记录当前非零插入位置，最后补零。

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int indexPos = 0;
        for(int i = 0; i < nums.size(); i++){
            if(nums[i] == 0)
                continue;
            if(i == indexPos)
                indexPos++;
            else{
                nums[indexPos] = nums[i];
                indexPos++;
            }
        }

        for(int i = indexPos; i < nums.size(); i++)
            nums[i] = 0;
    }
};

461 汉明距离

求两个int数的汉明距离，比较简单，自己实现的，位操作

class Solution {
public:
    int hammingDistance(int x, int y) {
        int count = 0;
        int z = x ^ y;
        while(z){
            if(z & 1)
                count++;
            z = z >> 1;
        }
        return count;
    }
};

448 找到所有数组中消失的数字

给一个长度为N的数组，找出数组在1到N之间没有出现的数字。nums = [4,3,2,7,8,2,3,1]，输出：[5,6]。要求时间复杂度为o（N），不适用额外空间。看别人的思路，通过遍历和交换，让所有数字归位，即数组中第一个位置是1，第二个位置是2……，再次遍历，不在其位的数字返回即可

class Solution {
public:
    vector<int> findDisappearedNumbers(vector<int>& nums) {
        vector<int> res;
        for(int i = 0; i < nums.size(); i++){
            if(nums[i] != nums[nums[i] - 1]){
                swap(nums[i], nums[nums[i] - 1]);
                i--;  //非常重要！画龙点睛的一行
            }              
        }

        for(int i = 0; i < nums.size(); i++){
            if(nums[i] != i + 1)
                res.push_back(i+1);
        }  
        return res;      

    }
};

581 最短无序连续子数组

找到一个数组的连续子数组，对这个子数组重新排序后，整个数组也有序。如果用排序，再比较不同，很简单，可以忽略此题

class Solution {
public:
    int findUnsortedSubarray(vector<int>& nums) {
        vector<int> sortNums = nums;
        sort(sortNums.begin(), sortNums.end());

        int leftIndex = -1, rightIndex = -2;  //为了匹配0的情况
        for(int i = 0 ; i < nums.size(); i ++){
            if(nums[i] != sortNums[i]){
                leftIndex = i;
                break;
            }
        }
        for(int i = nums.size() - 1; i >= 0; i--){
            if(nums[i] != sortNums[i]){
                rightIndex = i;
                break;
            }
        }
        return rightIndex - leftIndex + 1;
    }
};

26 删除有序数组中的重复项

删除有序数组vector里重复的元素，比较简单，vector删除元素使用erase()，迭代器位置注意下

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int len = nums.size();
        if(len <= 1)
            return len;
        int flag = nums[0];
        for(vector<int>::iterator iter = nums.begin() + 1; iter != nums.end(); iter++) {
            if(*iter == flag){
                nums.erase(iter);
                iter--; //删除该位置后，迭代器自动指向下一个位置列，这里要再减1 ！！
            }
            else{
                flag = *iter;
            }
        }
        return nums.size();

    }
};

66 加1

vector数组存放0-9的数字，相当于整个vector存放一个完整的整数，计算整数+1，返回新的vector，唯一注意的是如果是999样式，结果vector长读加一位，简单，可以不看

class Solution {
public:
    vector<int> plusOne(vector<int>& digits) {
        int len = digits.size();
        vector<int> resSum(len + 1, 0);
        int carry = 1;
        
        for(int i = len; i > 0; i--){
            resSum[i] = digits[i-1] + carry;
            if(resSum[i] == 10){
                resSum[i] = 0;
            }
            else{
                carry = 0;
            }
        }

        if(0 == carry){
            vector<int>::iterator iter = resSum.begin();
            resSum.erase(iter);
        }
        else{
            resSum[0] = 1;
        }
        return resSum;

    }
};

其他-面试相关

题目内容不便写出来，参考相关文档

验证图书出版码是否有效

#include

class Solution {
  public:
  string isRecognitionCode(string recgCode) {
      int recgNum = 0, weight = 1;
      string resOk = "right";
      string resUpdate(recgCode.substr(0, 12));
      for(int i = 0; i < recgCode.size(); i++){
          if(i == 1 || i == 5 || i > 10)
            continue;
          recgNum += (recgCode[i] - '0') * weight++;
      }
      recgNum = recgNum % 11;
      char lastChar;
      if(recgNum == 10)
        lastChar = 'x';
      else
        lastChar = '0' + recgNum;
      
      if(recgCode[12] == lastChar)
        return resOk;
      stringstream stream;
      stream << lastChar;
      resUpdate.append(stream.str());
      return resUpdate;
  }  
};

数字金字塔最大路径和

class Solution {
    public:
        int findMaxPath(vector<vector<int>>& nums) {
            if(nums.size() == 0)
                return 0;
            return dfsMaxPath(nums, 0, 0);

        }

        int dfsMaxPath(vector<vector<int>>& nums, int x, int y) {
            if(y == nums.size() - 1)
                return nums[y][x];
            int leftChild = dfsMaxPath(nums, x, y + 1);
            int rightChild = dfsMaxPath(nums, x + 1, y + 1);
            return nums[y][x] + (leftChild > rightChild? leftChild: rightChild);
        }
};

合并果子

题意可搜索，数组插入时要保证有序，这时就用到了优先队列

#include 
using namespace std;

int main()
{
    int n;
    cin>>n;
    //定义优先队列 
    priority_queue<int ,vector<int>,greater<int> >q;
    long long x;
    long long  sum=0;
    for(int i=1;i<=n;i=i+1)
    {
        cin>>x;
        //插入元素 
        q.push(x);
    }
    //当队列不为空 
    while(!q.empty())
    {
        long long a1=q.top();//取首元素 
        q.pop();//删除队列头元素 
        if(q.empty())
        {
            break;
        }
        long long a2=q.top();
        long long a3=a1+a2;
        sum=sum+a3;
        q.push(a3);
        q.pop();
    }
    cout<<sum;
}

两个数互为质数，互质判断

bool isrp(int a, int b){
	if(a==1||b==1)     // 两个正整数中，只有其中一个数值为1，两个正整数为互质数
		return true;
	while(1){          // 求出两个正整数的最大公约数
		int t = a%b;
		if(t == 0) break;
		else{
			a = b;
			b = t;
		}
	}
	if(b>1)	return false;// 如果最大公约数大于1，表示两个正整数不互质
	else return true;	// 如果最大公约数等于1,表示两个正整数互质