队列以及队列的应用
队列
队列的定义
生活中可能有很多种需要排队的场景,比如中午去食堂打饭,需要排队,排在队头的同学肯定是先去的,所以先打上饭。计算机中也有很多这样的场景,比如作业调度系统,如果同时来几个任务都需要用到输入输出系统,但是输入输出设备只有一套,谁先用呢,也是谁先来谁用,也需要排队。再比如我们的锁机制,如果出现多线程竞争同一把锁,那么同时只有一个线程获得了锁资源,剩下的线程怎么办呢,那如果是公平锁,肯定也是排队,等锁被释放了,那个最先来的线程优先获得锁资源。
那么根据上面的说法我们也大概了解了什么是队列。把他从生活中抽象成一个书本上的概念就是,允许在表的一端插入,另一端删除,插入的一端叫做队头,删除的一端叫做队尾。这就是队列的概念了。他的一大特性就是先进先出(FIFO),这是和栈的区别,栈是后进先出。
在进一步,我们可以用代码抽象出队列的接口。
public interface Queue<E> {
/**
* 队列中元素的个数
*
* @return size
*/
int getSize();
/**
* 队列是否为空
*
* @return e
*/
boolean isEmpty();
/**
* 入队
*
* @param e e
*/
void enqueue(E e);
/**
* 出队
*
* @return e
*/
E dequeue();
/**
* 查看对头元素
*
* @return e
*/
E getFront();
}
队列作为线性表的一种,那么他和栈一样,也是可以通过数组和链表实现的,下面我们分享一下代码,部分代码来自慕课网玩转数据结构。
数组实现队列
基本实现
public class ArrayQueue<E> implements Queue<E> {
Array<E> array;
public ArrayQueue(int capacity) {
array = new Array<>(capacity);
}
public ArrayQueue() {
array = new Array<>();
}
@Override
public int getSize() {
return array.getSize();
}
@Override
public boolean isEmpty() {
return array.isEmpty();
}
@Override
public void enqueue(E e) {
array.addLast(e);
}
@Override
public E dequeue() {
return array.removeFirst();
}
@Override
public E getFront() {
return array.get(0);
}
}
优化后的循环队列
数组实现队列的问题(假溢出)
假如现在有一个空队列,一次入队A B C三个元素,接着A B出对,然后D E F入队,此时看整个队列,如果限定了该队列长度为6,那么这个时候在想插入新元素就会发生溢出,因为已经到队尾了啊。但是其实这是一种假溢出,因为实际上A B出队后,他们的位置还空着,就像图中那两个灰色的位置。因此原来那种结构就有了一定的局限性,容易造成空间的浪费。
为了避免这种情况,把A B的位置充分利用起来,我们可以把数组的两头连接起来,在逻辑上把这个队列看成一个环,构造出一个循环队列,这样当G入队时候,我们就可以将G放到原来A的位置。
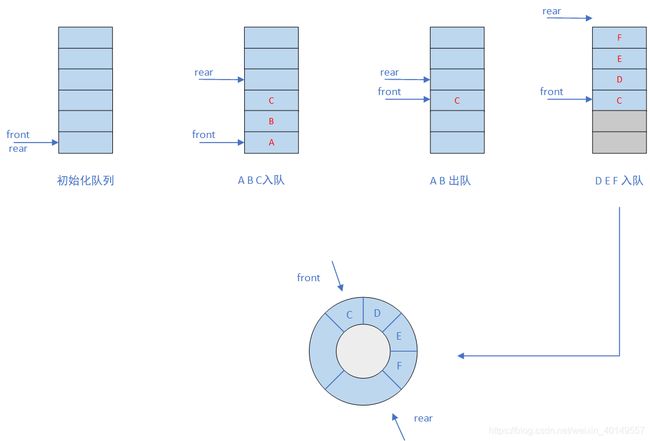
循环队列的入队出队操作
那接着上一节引出循环队列,我们在详细讨论一下循环队列具体的出队入队过程和一些细节。
我们用下图来表示一个循环队列,他的初始化状态是一个空队列,没有一个元素,这个时候队头和队尾都指向我们的0号位置(front == rear,用来标志队列空)。接着A入队,这个时候rear顺时针移动到1号位置。front不变。继续让B C D E F G入队,最终rear移动到了7号位置。这个时候我们的队列还是有空位置的,那么假设在来一个H元素,可以让他入队吗,假设可以,那么rear在顺时针移动一个位置,到了0号位置,这个时候front == rear。前面我们说过用front == rear来标志队列空的啊,现在队列满也成这样了,怎么办呢?因此呢,肯定这个时候不能让H入队的,当rear到7号位置的时候,就应该已经标志队列是满的。因此假设队列的最大容量是maxSize,那么这一步就可以得出如何区别队列空和队列满的条件:队列空(front == rear),队列满((rear + 1) % maxSize == front)。
然后继续让A出队,这个时候front顺时针移动一个位置,0位置就空出来了,队头就成1号位置了。然后再来H入队,这个时候H是可以入队的,H放到7号位置,rear移动到0号位置,那么这个0是怎么算来的呢,是不是可以用求余数的方式算呢,(7 + 1) % 8 = 0。那么当未来某一天队列一直出队,front来到这里的时候,他的位置是不是也可以用同样的位置计算呢。因此又得出两个公式。当front和rear指针到达size - 1位置后,在前进一个一个位置,就又开始回到原点循环了,他们的位置可以这样表示:front = (front + 1) % maxSize,rear = (rear + 1) % maxSize。

代码实现
public class LoopQueue<E> implements Queue<E> {
private E[] data;
private int front;
private int rear;
private int size;
public LoopQueue(int capacity) {
// 因为用了front = size - 1判断队列满,
// 所以实际初始化capacity的队列只能放capacity - 1个元素
data = (E[]) new Object[capacity + 1];
front = 0;
rear = 0;
size = 0;
}
public LoopQueue() {
this(10);
}
@Override
public int getSize() {
return size;
}
@Override
public boolean isEmpty() {
return rear == front;
}
@Override
public void enqueue(E e) {
if (isFull()) {
throw new ArrayIndexOutOfBoundsException("queue is full");
}
data[rear] = e;
rear = (rear + 1) % data.length;
size++;
}
@Override
public E dequeue() {
if (isEmpty()) {
throw new IllegalArgumentException("queue is empty");
}
E result = data[front];
data[front] = null;
front = (front + 1) % data.length;
size--;
return result;
}
@Override
public E getFront() {
if (isEmpty()) {
throw new IllegalArgumentException("queue is empty");
}
return data[front];
}
// 队列是否满
private boolean isFull() {
if (size == 0) {
return false;
}
return (rear + 1) % data.length == front;
}
}
链表实现队列
用链表实现队列也是很简单的,链表的第一个节点作为队头,最后一个节点作为队尾。入队就在链表尾加一个节点,出队就删除链表头。这些都可以参考链表那一节。并且链表不会有溢出的问题,因为链表是真正的线性表里能动态扩容的数据结构。
public class LinkedListQueue<E> implements Queue<E> {
private class Node{
public E e;
public Node next;
public Node(E e, Node next){
this.e = e;
this.next = next;
}
public Node(E e){
this(e, null);
}
public Node(){
this(null, null);
}
@Override
public String toString(){
return e.toString();
}
}
private Node head, tail;
private int size;
public LinkedListQueue() {
this.tail = null;
this.head = null;
size = 0;
}
@Override
public int getSize() {
return size;
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public void enqueue(E e) {
if (tail == null) {
tail = new Node(e);
head = tail;
} else {
tail.next = new Node(e);
tail = tail.next;
}
size++;
}
@Override
public E dequeue() {
if (isEmpty()) {
throw new IllegalArgumentException("queue is empty");
}
Node node = head;
head = head.next;
node.next = null;
if (head == null) {
tail = null;
}
size--;
return node.e;
}
@Override
public E getFront() {
if (isEmpty()) {
throw new IllegalArgumentException("queue is empty");
}
return head.e;
}
}
优先队列
优先队列完了在堆那一节详细讨论。
队列的应用
线程池中的应用
在java的线程池TreadPoolExecutor中就用到了队列这种数据结构。线程池主要用来管理线程,提高线程的利用率,防止频繁的创建销毁线程带来的性能消耗。他的主要原理分为以下几步:
- 当有任务提交到线程池,线程池首先会根据核心线程数创建线程来处理这些任务
- 如果核心线程处理不过来,就放到一个阻塞队列等待,这里就用到了队列这种数据结构
- 如果任务在继续来,阻塞队列放不下了,就会创建一些临时线程来处理
- 如果临时线程也用完了,就开启拒绝策略。

AQS中的应用
J.U.C包下的抽象队列同步器作为并发包下锁的一个基础框架,就用到了队列这种数据结构。我们知道多个线程竞争锁资源的时候,同时肯定只能又一个线程获得锁,那么剩下的线程怎么办呢?AQS为我们提供了一个基于双向链表实现的同步队列,剩下没有获得锁的线程就让他到这个同步队列中去等待。等当前线程释放锁以后,如果是公平锁,就从队列头取出一个线程,让他去拿锁资源。
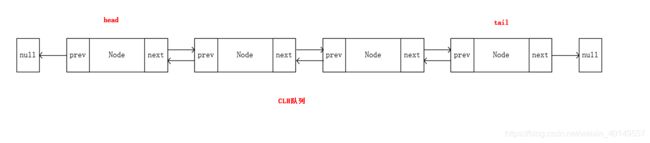
消息队列中的应用
消息队列顾名思义就可以看出是基于队列实现的。Kafka等不太了解,在RocketMQ中,就大量使用了队列这种数据结构,比如每个broker启动后,会为每一个topic默认创建四个消息队列,用来存储消息生产者生产的消息。并且在事务消息中,也是用了队列来存储半事务消息。
具体代码参见github
