01背包(一) 01背包(二)动态规划
01背包(一) 二维数组
题目
背包最大重量为4。
物品为:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
问背包能背的物品最大价值是多少?
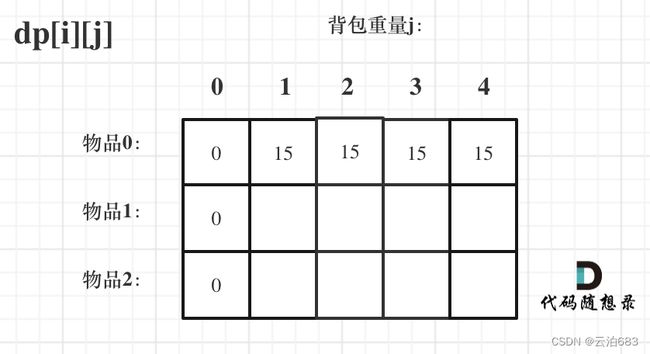
创建二维数组,dp[i][j]的含义是任意放入前 i 个物品放进在背包重量为j的时候的最大价值
递推公式
dp[i][j] = max( dp[i - 1][j] , dp[i - 1][j - weight[i]] + value[i] );dp[i][j](任意放入前 i 个物品 放进 j容量背包的最大价值) 可以由 dp[i - 1][j](任意放入前 i -1个物品但不放物品 i 的最大价值)和
dp[i - 1][j - weight[i]] + value[i] (任意放入前 i-1 个物品 同时 放物品 i 的最大价值)推出
初始化
初始化 dp[i][0](任意放入前 i 个物品,同时背包容量为 0 的最大价值),也就是价值 “0” 的那一列。
容量为0,放不了物品,价值为0
初始化 dp[0][j](放入物品0,背包容量为 j 的最大价值),也就是 价值“15”的那四个格子。
//初始化 dp[i][0](放入物品i,背包容量为 0 的最大价值)
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
//初始化 dp[0][j](放入物品0,背包容量为 j 的最大价值)
for (int j = 0 ; j < weight[0]; j++) {
dp[0][j] = 0;
}
后面变成,先全赋值为0,省去背包容量为0的初始赋值,然后赋放入物品0的值
// 初始化 dp
vector> dp(weight.size(), vector(bagweight + 1, 0));
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
} 总代码
先遍历物品再遍历背包容量
void test_2_wei_bag_problem1() {
vector weight = {1, 3, 4};
vector value = {15, 20, 30};
int bagweight = 4;
// 二维数组
vector> dp(weight.size(), vector(bagweight + 1, 0));
// 初始化
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
// weight数组的大小 就是物品个数
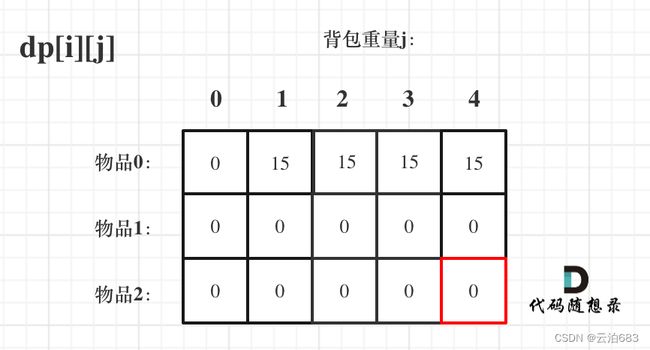
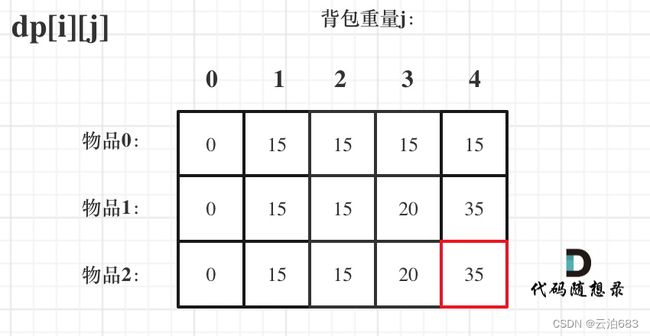
for(int i = 1; i < weight.size(); i++) { // 遍历物品
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j];//如果背包容量不够-不加
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
//如果容量够,看看加上价值大还是不加上价值大,因为背包是有容量的
}
}
//这个就是右下角,遍历完成的最大价值,因为有0占格子所以-1
cout << dp[weight.size() - 1][bagweight] << endl;
}
int main() {
test_2_wei_bag_problem1();
}
想法:这也是遍历了每一种 背包容量 和 物品和不放物品 的所有情况了吧,每一种情况都判断出最大价值,由上一次的最大价值推出下一次的最大价值,末尾得出答案。
02背包(二) 一维数组
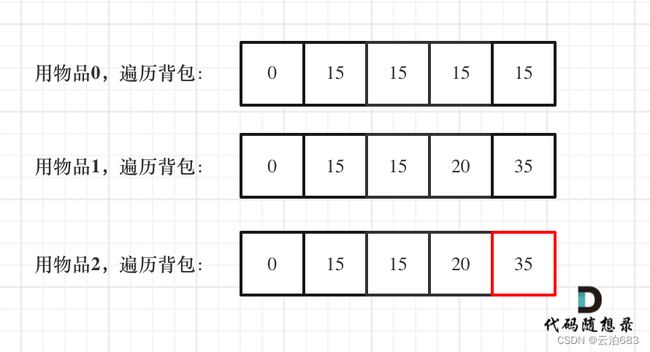
可以从二维简化为一维的数组,理由是可以第一行初始化了以后,后面的行可以重复覆盖第一行来得到最后的结果,dp[i][j]只依靠他的左边和正上方推出,变成一维数组不断覆盖后也不影响最终结果的推导(原来二维数组的最右下角是结果)
题目同(一)
递推公式
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);dp[j] 等于 没放入i的最大价值,dp[j - weight[i]] + value[i] 等于 放入i的最大价值
怎么得出的?
原来二维数组的递推公式 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i],在递推过程中(左到右上到下),遍历物品1的时候,会用物品1其上方,遍历物品0的值,来计算遍历到的这个格子的值。
如果采取覆盖的方式,把二维数组变成一维数组,利用正上方的值变成利用本格的值,利用完后再替换成计算出的结果,就可以只用一行完成多行的计算了。
比如dp[i - 1]变成dp[i]就是这个意思,dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]
然后可以再去除i,只留下这样的话就去掉了 i 的维度了,但是还是用到i的,我的理解这是一种简化的写法。然后变成
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
初始化
vector dp(bagWeight + 1, 0);
遍历顺序
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);从后往前计算 为什么?
正序遍历
dp[1] = dp[1 - weight[0]] + value[0] = 15(这个时候dp[1]=15)
dp[2] = dp[2 - weight[0]] + value[0] = 30
此时dp[2]就已经是30了,意味着物品0,被放入了两次,所以不能正序遍历。
为什么倒序遍历,就可以保证物品只放入一次呢?
倒序就是先算dp[2]
倒序遍历
dp[2] = dp[2 - weight[0]] + value[0] = 15 (数组已经都初始化为0,就是意思这个时候dp[1]=0)
dp[1] = dp[1 - weight[0]] + value[0] = 15
我的理解就是,一维正序遍历中,正在遍历的值会使用前面的值,比如dp[2]使用dp[1]的,一个dp[1]=15,一个等于0,因为是一个是后序初始化为0还没有计算成15,一个是正序先计算了成15了,但不就是要使用前面的值吗?为什么不使用?
原因是正序计算出的15,覆盖后的值而不是覆盖前的值,而dp[2]需要的dp[1]是覆盖前的值。
换成二维数组和他的递归公式dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i],就是,覆盖前的值才是上一列前面的值,覆盖后就是下一列前面的值了。
这也是为啥二维数组正序倒序都可以,而一维数组只能倒序的原因。
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
总代码
void test_1_wei_bag_problem() {
vector weight = {1, 3, 4};
vector value = {15, 20, 30};
int bagWeight = 4;
// 初始化
vector dp(bagWeight + 1, 0);
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
cout << dp[bagWeight] << endl;
}
int main() {
test_1_wei_bag_problem();
} 着实是有些抽象的。。