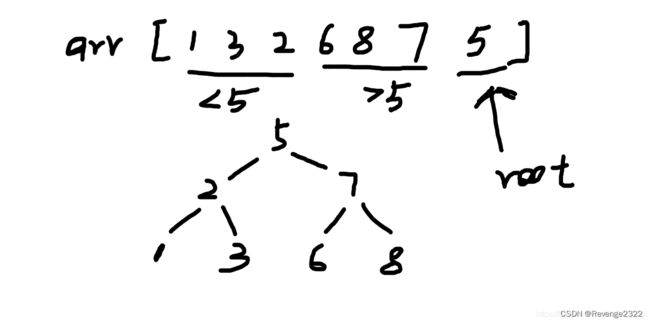构建二叉树模板大全
目录
前言:
从中序与后序遍历序列构造二叉树
从前序与中序遍历序列构造二叉树
根据前序和后序遍历构造二叉树
构造二叉搜索树
一.概念
中序遍历数组构造二叉树
后续遍历数组构造二叉搜索树
前序遍历数组构造二叉搜索树
总结:
前言:
有许多关于构建二叉树的题目,并且这些题目有固定的模板,我将对这类题目将进行分类总结。本篇致力于让读者能够融会贯通,抓住要领,建立模板化思维,看见一题想到一类。
从中序与后序遍历序列构造二叉树
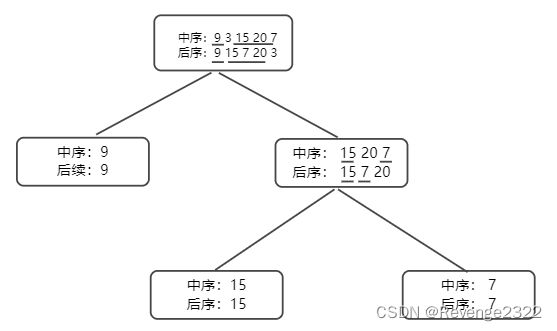
题目:106. 从中序与后序遍历序列构造二叉树
根据题目来进行分析,我们拿到的条件是
后序数组: 我们知道后序数组的最后一位就是当前二叉树的根节点。
中序数组: 我们得知根据根节点可以将数组分为两部分,左边用来构造左子树,右边用来构造右子树。
综合分析:后序数组用来确定根节点,中序数组用来不断的划分左子树,右子树。
过程: 我们将两个数组并排放置,我们从后序数组中取出当前根节点,让后从中序数组中找到该根节点,以此为中心分别划分出来左区间,和右区间。再递归构造左子树和右子树。
递归:
1.确定函数返回类型:根据题目可以知道,需要返回的是TreeNode* 。
2.确定终止条件:如果数组的长度为零的时候,返回NULL。如果数组长度为1的时候返回新创建的节点。
(有人会问:为什么这里终止条件有两个?一个是长度为零,一个是长度为一,按照做题经验来说一般不是直接拿空节点作为终止条件么?)
解答:这个问题确实思考的比较深入。终止条件怎么能写两个捏???很多讲递归的老师都会模棱两可的说因为就剩一个节点了,所以要返回。 那你把这当终止条件你要我空节点干嘛??
小伙伴们不要着急,请看如下
其实如果不加第二个终止条件效率会变很低,但仍然可以解出来。假如我发现长度为一的数组后,我就没必要再判断NULL节点了。所以其实是用来提高效率的。
3.最后一层递归条件:找到后序数组最后一个元素在中序数组的位置,作为切割点切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组切割后序数组)切成后序左数组和后序右数组递归处理左区间和右区间。
代码如下:
确定终止条件
if(postorder.size()==0) return nullptr;
TreeNode* element=new TreeNode(postorder[postorder.size()-1]);
if(postorder.size()==1) return element;这里先判断数组长度是不是为零,让后再创建新节点,最后再附加一条判断数组长度是不是一。
分割数组
int i=0;
for(;i in_ord_first(inorder.begin(),inorder.begin()+i);
vector in_ord_second(inorder.begin()+i+1,inorder.end());
postorder.resize(postorder.size()-1);
vector pos_ord_first(postorder.begin(),postorder.begin()+in_ord_first.size());
vector pos_ord_second(postorder.begin()+in_ord_first.size(),postorder.end()); 分割中序数组,先在中序数组中找到根节点。定位到根节点的下标以后,将数组进行分割,创建新的数组vector
让后思考,后序数组如何分割??第一步先除去根元素 postorder.resize(postorder.size()-1);
然后通过并排对比发现,此时有一个很重的点,就是中序数组大小一定是和后序数组的大小相同的(这是必然)中序数组我们都切成了左中序数组和右中序数组了,那么后序数组就可以按照左中序数组的大小来切割,切成左后序数组和右后序数组。
vector pos_ord_first(postorder.begin(),postorder.begin()+in_ord_first.size());
vector pos_ord_second(postorder.begin()+in_ord_first.size(),postorder.end()); 最后一层递归条件:我们最后只需要把已经构建好的左子树,和已经构建好的右子树返回给element节点即可,然后返回element 根节点。
element->left=buildTree(in_ord_first,pos_ord_first);
element->right=buildTree(in_ord_second,pos_ord_second);
return element;(ps:递归如果看的不太懂,看我博客递归统一化模板)
整体代码如下:
class Solution {
public:
TreeNode* buildTree(vector& inorder, vector& postorder) {
if(postorder.size()==0) return nullptr;
TreeNode* element=new TreeNode(postorder[postorder.size()-1]);
if(postorder.size()==1) return element;
int i=0;
for(;i in_ord_first(inorder.begin(),inorder.begin()+i);
vector in_ord_second(inorder.begin()+i+1,inorder.end());
postorder.resize(postorder.size()-1);
vector pos_ord_first(postorder.begin(),postorder.begin()+in_ord_first.size());
vector pos_ord_second(postorder.begin()+in_ord_first.size(),postorder.end());
element->left=buildTree(in_ord_first,pos_ord_first);
element->right=buildTree(in_ord_second,pos_ord_second);
return element;
}
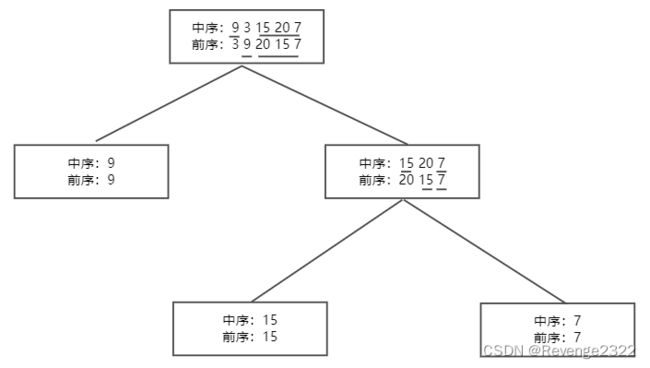
}; 从前序与中序遍历序列构造二叉树
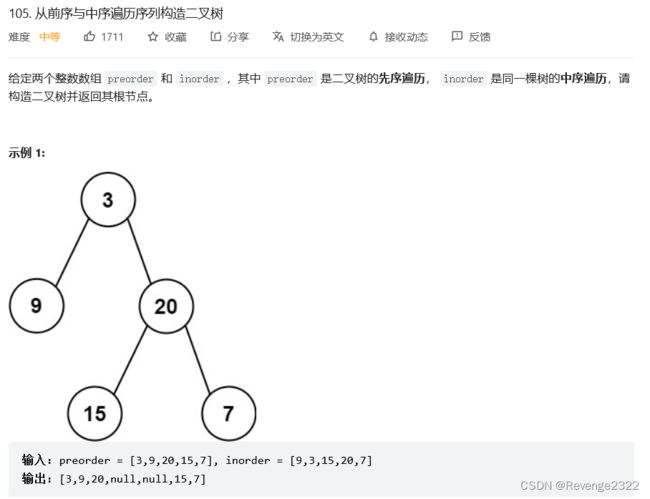
题目:105. 从前序与中序遍历序列构造二叉树
根据题目来进行分析,我们拿到的条件是
前序数组: 我们知道前序数组的第一位就是当前二叉树的根节点。
中序数组: 我们得知根据根节点可以将数组分为两部分,左边用来构造左子树,右边用来构造右子树。
综合分析:后序数组用来确定根节点,中序数组用来不断的划分左子树,右子树。
过程: 我们将两个数组并排放置,我们从后序数组中取出当前根节点,让后从中序数组中找到该根节点,以此为中心分别划分出来左区间,和右区间。再递归构造左子树和右子树。
递归:
1.确定函数返回类型:根据题目可以知道,需要返回的是TreeNode* 。
2.确定终止条件:如果数组的长度为零的时候,返回NULL。如果数组长度为1的时候返回新创建的节点。
3.最后一层递归条件:找到前序数组第一个元素在中序数组的位置,作为切割点切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组切割前序数组)切成前序左数组和前序右数组递归处理左区间和右区间。
整体代码如下:
class Solution {
public:
TreeNode* buildTree(vector& preorder, vector& inorder) {
if(preorder.size()==0) return nullptr;
TreeNode* element=new TreeNode(preorder[0]);
if(preorder.size()==1) return element;
int i=0;
for(;i in_ord_first(inorder.begin(),inorder.begin()+i);
vector in_ord_second(inorder.begin()+i+1,inorder.end());
vector new_preorder(preorder.begin()+1,preorder.end());
vector pre_ord_first(new_preorder.begin(),new_preorder.begin()+in_ord_first.size());
vector pre_ord_second(new_preorder.begin()+in_ord_first.size(),new_preorder.end());
element->left=buildTree(pre_ord_first,in_ord_first);
element->right=buildTree(pre_ord_second,in_ord_second);
return element;
}
}; 根据前序和后序遍历构造二叉树
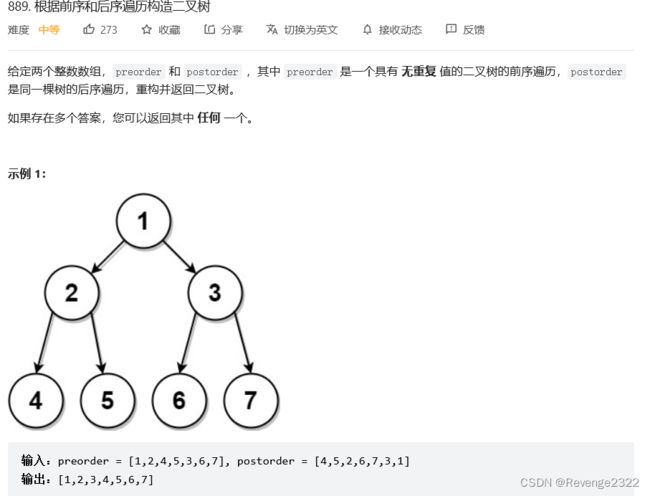
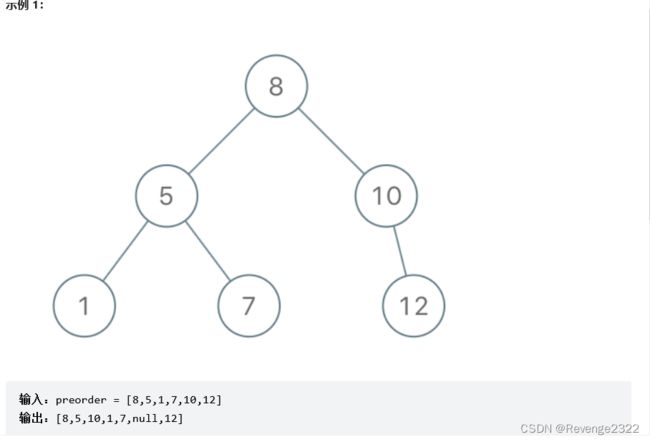
题目:889. 根据前序和后序遍历构造二叉树
思路
前序遍历为:
(根结点) (前序遍历左分支) (前序遍历右分支)
而后序遍历为:
(后序遍历左分支) (后序遍历右分支) (根结点)
例如,如果最终的二叉树可以被序列化的表述为 [1, 2, 3, 4, 5, 6, 7],那么其前序遍历为 [1] + [2, 4, 5] + [3, 6, 7],而后序遍历为 [4, 5, 2] + [6, 7, 3] + [1].
如果我们知道左分支有多少个结点,我们就可以对这些数组进行分组,并用递归生成树的每个分
这道题跟前两个思路大同小异。
递归:
1.确定函数返回类型:根据题目可以知道,需要返回的是TreeNode* 。
2.确定终止条件:如果数组的长度为零的时候,返回NULL。如果数组长度为1的时候返回新创建的节点。
3.最后一层递归条件:找到前序数组第二个元素在后序数组的位置,作为切割点切割后序数组,切成后序左数组和中序右数组 (顺序别搞反了,一定是先切后序数组切割前序数组)切成后序左数组和后序右数组递归处理左区间和右区间。
代码如下:
class Solution {
public:
TreeNode* constructFromPrePost(vector& preorder, vector& postorder) {
if(preorder.size()==0) return nullptr;
TreeNode* element=new TreeNode(preorder[0]);
if(preorder.size()==1) return element;
postorder.resize(postorder.size()-1);
int i=0;
for(;i pos_ord_first(postorder.begin(),postorder.begin()+i+1);
vector pos_ord_second(postorder.begin()+i+1,postorder.end());
vector new_preorder(preorder.begin()+1,preorder.end());
vector pre_ord_first(new_preorder.begin(),new_preorder.begin()+pos_ord_first.size());
vector pre_ord_second(new_preorder.begin()+pos_ord_first.size(),new_preorder.end());
element->left=constructFromPrePost(pre_ord_first,pos_ord_first);
element->right=constructFromPrePost(pre_ord_second,pos_ord_second);
return element;
}
}; 构造二叉搜索树
一.概念
二叉搜索树又称二叉排序树,具有以下性质:
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树
请牢牢的记住这句话:中序遍历二叉搜索树等于遍历有序数组。
中序遍历数组构造二叉树
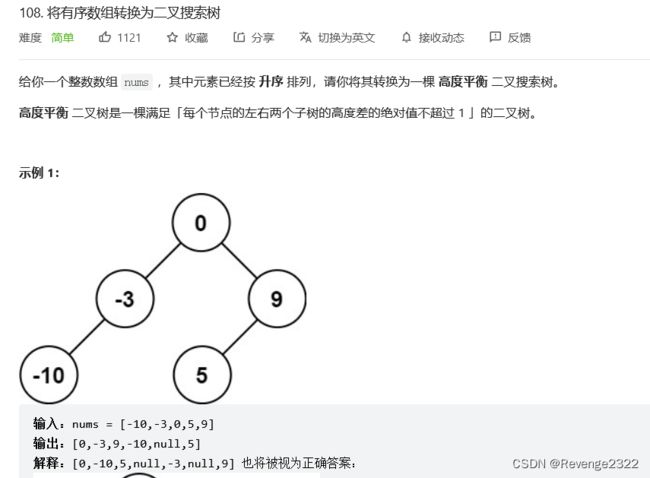
题目:108. 将有序数组转换为二叉搜索树
当我们遍历有序数组时候,他的中间值就是根节点。所以我们每次都取数组的中间值当根节点,同时该数组一分为二变为左数组,右数组,不断重复该过程,直到数组的大小为零即构建完成。
class Solution {
private:
TreeNode* traversal(vector& nums, int left, int right) {
if (left > right) return nullptr;
int mid = left + ((right - left) / 2);
TreeNode* root = new TreeNode(nums[mid]);
root->left = traversal(nums, left, mid - 1);
root->right = traversal(nums, mid + 1, right);
return root;
}
public:
TreeNode* sortedArrayToBST(vector& nums) {
TreeNode* root = traversal(nums, 0, nums.size() - 1);
return root;
}
}; 因为每一个过程都是相同的,所以符合递归性质。
left 和 right 用于控制每个新数组的大小,当left>right 时代表数组的大小为0递归结束。
所以终止条件是left>right.
操作过程: 创建新的节点 new TreeNode (nums[mid])。
最后一层递归条件:root 左子树结果返回给根节点。 root->left = traversal(nums, left, mid - 1);
root 右子树结果返回给根节点。 root->right = traversal(nums, mid+1,right);
这里着重强调一下边界条件:
因为traveral(nums,left,right) 是【 left ,right 】 是左闭右闭。所以每次划分得抛去mid 。
不清楚递归的可以看我的这篇博客 递归统一化模板_Revenge2322的博客-CSDN博客 。
后续遍历数组构造二叉搜索树
后续遍历数组特点:最后一个节点是root根节点
然后我们需要找到分界点mid ,分界点mid其实是从后往前找第一个小于5的数的下标。
将剩下的划分为左数组,和右数组,左边数组接在root->left上
右边数组接在root->right上。
TreeNode* traversal(vector& nums,int left ,int right) {
if(left>right) return nullptr;
TreeNode* root=new TreeNode(nums[right]);
int mid=right;
for(int i=left;ileft=traversal(nums,left,mid-1);
root->right=traversal(nums,mid,right-1);
return root;
}
前序遍历数组构造二叉搜索树
题目:1008. 前序遍历构造二叉搜索树
TreeNode* traversal(vector& nums,int left ,int right) {
if(left>right) return nullptr;
TreeNode* root=new TreeNode(nums[left]);
int mid=left;
for(int i=right;i>left;i--)
{
if(nums[i]<=nums[left])
{
mid=i;
break;
}
}
root->left=traversal(nums,left+1,mid);
root->right=traversal(nums,mid+1,right);
return root;
}
这个跟后序数组构造二叉搜索树思路一样,不再重复。
总结:
构造二叉树一般分为构造普通的二叉树,和构造二叉搜索树。 构造二叉树我们学会一种思想,就是第一步先找当前根节点看哪一个数组能够明确确定根节点。第二步划分左区间,右区间。这里需要考察的是对vector的掌握,明确左开右闭,并且如何拷贝,如何resize。
二叉搜索树的构建,也是先寻找当前根节点。只不过这里是对一个vector进行操作,反而更加简单了,但是同样要注意区间开闭,这里没有对vector进行修改,而是用下标left,right代替划分区间,所以是左闭右闭。
更为震撼的是二叉搜索树的构建,以后将有更大的作用。欢迎看续集
二叉搜索树统一化解题模板_Revenge2322的博客-CSDN博客