蓝桥杯2016-Java B组省赛真题

前言

本文章只包含题目+答案，没有详细的分析过程（仅为了个人的归纳复盘使用）

题目以及讲解是看B站的视频：2016-Java-B题1煤球数目-1(C)_哔哩哔哩_bilibili

2016-Java省赛第一题——煤球数目

//煤球数目
public class Main0 {

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int pre = 1;//每一层
        int plus = 2;//增量
        long sum = 1;
        for (int k = 2; k <=100; k++) {
            sum += pre+plus;
            pre = pre + plus;
            plus++;
        }
        System.out.println(sum);
    }

}

答案：171700

关于这题的tips：

热身题，找规律，+2+3+4+......

2016-Java省赛第二题——生日蜡烛

//生日蜡烛
public class Main {

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        for (int i = 1; i < 100; i++) {
            for (int j = i; j < 100; j++) {
                if((i+j)*(j-i+1)/2==236){
                    System.out.println(i);
                }
            }
        }
    }

}

答案：26

关于这题的tips：

等差数列求和公式

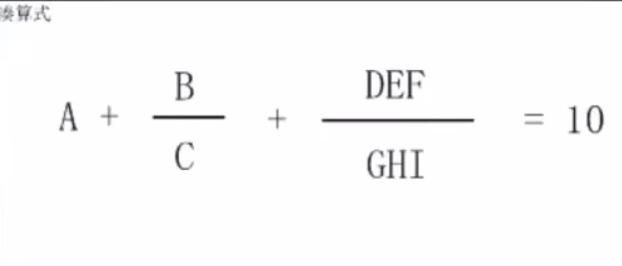
2016-Java省赛第三题——凑算式

//凑算式_全排列
public class Main {
    static int a[] = {1,2,3,4,5,6,7,8,9};
    static int ans;
    
    static boolean check(){
        int x = a[3]*100+a[4]*10+a[5];
        int y = a[6]*100+a[7]*10+a[8];
        if((a[1]*y+a[2]*x)%(y*a[2])==0 && a[0]+(a[1]*y+a[2]*x)/(y*a[2])==10)
            return true;
        return false;
    }
    
    /*递归回溯生成全排列，适用于无重复元素的情况
     * 考虑第k位，前面已经排定
     */
    static void f(int k){
        if(k==9){//一种排列已产生
            if(check())
                ans++;
        }
        
        //从k往后的每个数字都可以放在k位
        for(int i=k;i<9;i++){
            int t = a[i];
            a[i] = a[k];
            a[k] = t;
            
            f(k+1);
            
            t = a[i];
            a[i] = a[k];
            a[k] = t;
        }
    }
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        f(0);
        System.out.println(ans);
    }

}

答案：29

关于这题的tips:

用全排列的模板就能做出来，在我关于蓝桥杯2013年JavaB组真题的博客中就有相应的模板

2016-Java省赛第四题——分小组

//分小组
public class Main {
    //remain(剩余)
     public static String remain(int[] a){
         String s = "";
         for (int i = 0; i < a.length; i++) {
            if(a[i]==0) s+=(char)(i+'A');
        }
         return s;
     }
     static int cnt;
     
     public static void f(String s,int[] a){
         for (int i = 0; i < a.length; i++) {
            if(a[i]==1) continue;
            a[i] = 1;
            for (int j = i+1; j < a.length; j++) {
                if(a[j]==1) continue;
                a[j] = 1;
                for (int k = j+1; k < a.length; k++) {
                    if(a[k]==1) continue;
                    a[k] = 1;
                    System.out.println(s+" "+(char)(i+'A') + (char)(j+'A')+(char)(k+'A')+" "+remain(a));//填空
                    cnt++;
                    a[k] = 0;
                }
                a[j] = 0;
            }
            a[i] = 0;
        }
     }
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int[] a = new int[9];
        a[0] = 1;
        for (int b = 1; b < a.length; b++) {
            a[b] = 1;
            for (int c = b+1; c < a.length; c++) {
                a[c] = 1;
                String s = "A" + (char)(b+'A') + (char)(c+'A');
                f(s,a);
                a[c] = 0;
            }
            a[b] = 0;
        }
        System.out.println(cnt);
    }

}

答案：s+" "+(char)(i+'A') + (char)(j+'A')+(char)(k+'A')+" "+remain(a)

关于本题的tips：

逻辑推理，可以先注释掉需要填空的地方，然后再debug一下一步一步凑

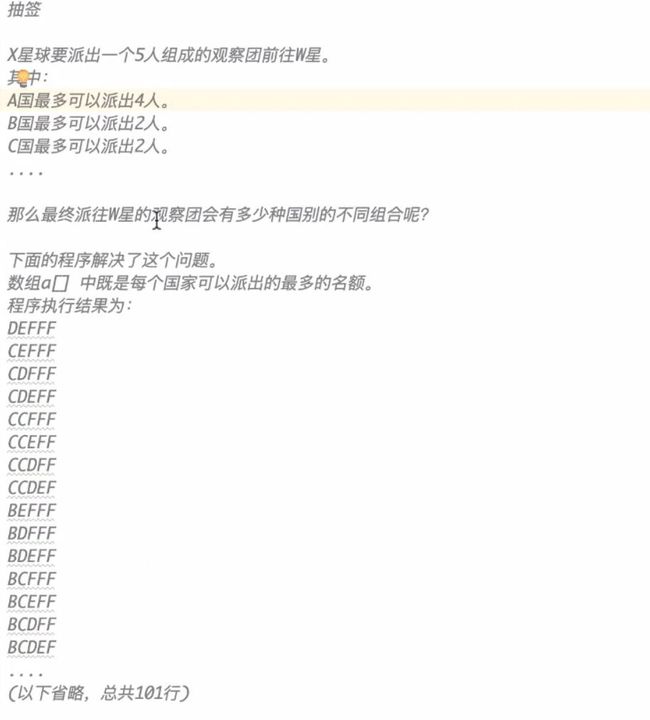
2016-Java省赛第五题——抽签

//抽签_递归
public class Main {
     
    public static void f(int[] a,int k,int n,String s) {
        if(k==a.length){
            if(n==0) System.out.println(s);
            return;
        }
        String s2 = s;
        for (int i = 0; i <= a[k]; i++) {
            f(a,k+1,n-i,s2);
            s2+= (char)(k+'A');
        }
    }
    
    
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int[] a = {4,2,2,1,1,3};
        
        f(a,0,5,"");
    }

}

答案：f(a,k+1,n-i,s2);

关于这题的tips：

需要搞清楚参数的含义和参数的变化方向

2016-Java省赛第六题——方格填数

//方格填数_全排列
public class Main {
    static int[] a = {0,1,2,3,4,5,6,7,8,9};
    static int ans;
    
    static boolean check(){
        //0和1不能相邻，和3不能相邻......
        if(Math.abs(a[0]-a[1])==1||
           Math.abs(a[0]-a[3])==1||
           Math.abs(a[0]-a[4])==1||
           Math.abs(a[0]-a[5])==1||
           
           Math.abs(a[1]-a[2])==1||
           Math.abs(a[1]-a[4])==1||
           Math.abs(a[1]-a[5])==1||
           Math.abs(a[1]-a[6])==1||
           
           Math.abs(a[2]-a[5])==1||
           Math.abs(a[2]-a[6])==1||
           
           Math.abs(a[3]-a[4])==1||
           Math.abs(a[3]-a[7])==1||
           Math.abs(a[3]-a[8])==1||
           
           Math.abs(a[4]-a[5])==1||
           Math.abs(a[4]-a[7])==1||
           Math.abs(a[4]-a[8])==1||
           Math.abs(a[4]-a[9])==1||
           
           Math.abs(a[5]-a[6])==1||
           Math.abs(a[5]-a[8])==1||
           Math.abs(a[5]-a[9])==1||
           
           Math.abs(a[6]-a[9])==1||
           
           Math.abs(a[7]-a[8])==1||
           
           Math.abs(a[8]-a[9])==1)
            return false;
        return true;
    }
    
    /*考虑第k个位置，一般从0开始*/
    static void f(int k){
        //出口
        if(k==10){
            boolean b = check();
            if(b)
                ans++;
            return;
        }
        
        for(int i=k;i<10;i++){
            //尝试将位置i与位置k交换，以此确定k位的值
            int t = a[i];
            a[i] = a[k];
            a[k] = t;
            
            f(k+1);
            
            //回溯
            t = a[i];
            a[i] = a[k];
            a[k] = t;
        }
    }
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        f(0);
        System.out.println(ans);
    }

}

答案：1580

关于这题的tips：

这题就是考全排列，每次考到全排列都是同一个模板，就是把check()方法重写一下就好

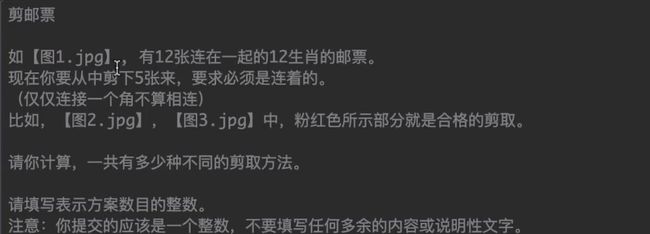
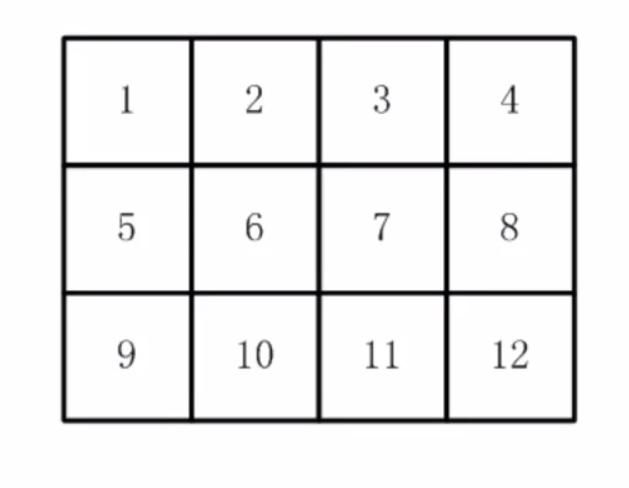
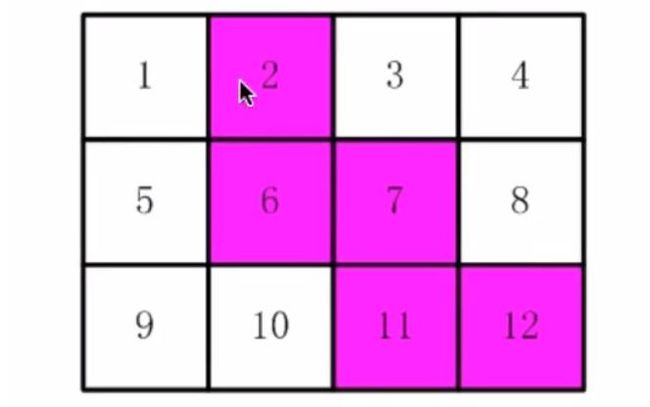
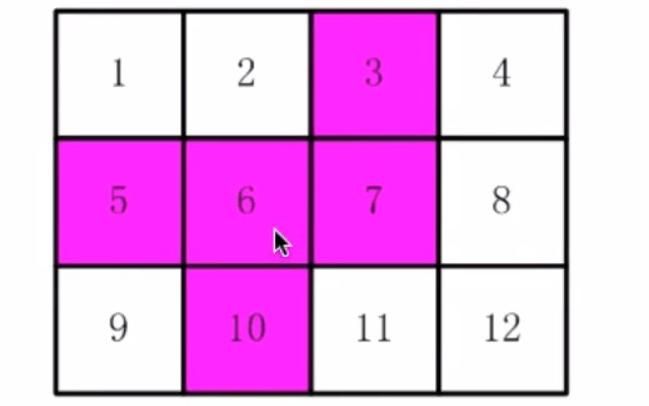
2016-Java省赛第七题——剪邮票

//剪邮票_深搜dfs_全排列
/*枚举所有的5张牌的组合
 * 检查他们是不是一个连通块
 */
public class Main {
    static int[] a = {0,0,0,0,0,0,0,1,1,1,1,1};//它的每个排列代表着12选5的一个方案
    static int ans;
    
    //dfs做连通性检查
    static void dfs(int g[][],int i,int j){
        g[i][j] = 0;
        if(i-1>=0 && g[i-1][j]==1) dfs(g,i-1,j);
        if(i+1<=2 && g[i+1][j]==1) dfs(g,i+1,j);
        if(j-1>=0 && g[i][j-1]==1) dfs(g,i,j-1);
        if(j+1<=3 && g[i][j+1]==1) dfs(g,i,j+1);
    }
    
    static boolean check(int path[]){
        int g[][] = new int[3][4];
        //将某个排列映射到二维矩阵上
        for (int i = 0; i < 3; i++) {
            for (int j = 0; j < 4; j++) {
                if(path[i*4+j]==1) g[i][j]=1;
                else g[i][j] = 0;
            }
        }
        int cnt = 0;//连通块的数目
        //g上面就有5个格子被标记为1，现在才用dfs做连通性检查，要求只有一个连通块
        for (int i = 0; i < 3; i++) {
            for (int j = 0; j < 4; j++) {
                if(g[i][j]==1){
                    dfs(g,i,j);
                    cnt++;
                   }
                }
            }
        return cnt == 1;
        
    } 
    
    static boolean vis[] = new boolean[12];
    static void f(int k,int path[]){
        if(k==12){
            if(check(path)){
                ans++;
            }
        }
        for (int i = 0; i < 12; i++) {
            if(i>0 && a[i]==a[i-1] && !vis[i-1]) continue;//现在准备选取的元素和上一个元素相同，但是上一个元素还没有被使用
            if(!vis[i]){//没有被用过的元素可以抓到path中
                vis[i] = true;//标记为已访问
                path[k] = a[i];//将a[i]填入到path[k]中
                f(k+1,path);//递归
                vis[i] = false;//回溯
                
            }
        }
    }
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int path[] = new int[12];
        f(0,path);
        System.out.println(ans);
    }

}

答案：116

关于这题的tips：

1. 先用生成全排列（不会有重复方法的全排列）

2. 用vis[]数组去标记每一块是否有被访问过

3. 将排列映射到二维矩阵上，进行连通性检测

2016-Java省赛第八题——四平方和

import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;

//四平方和_暴力枚举_枚举的优化
public class Main {
    
    static int N;
    static Map cache = new HashMap();
    
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        Scanner sc = new Scanner(System.in);
        N = sc.nextInt();
        //缓存
        for (int c = 0; c*c <= N/2; c++) {
            for (int d = 0; c*c+d*d<= N; d++) {
                if(cache.get(c*c+d*d)==null){
                    cache.put(c*c+d*d, c);//映射
                }
            }
        }
        
        for (int a = 0; a*a <= N/4; a++) {
            for (int b = a; a*a+b*b<= N/2; b++) {
                if(cache.get(N-a*a-b*b)!=null){
                    int c = cache.get(N-a*a-b*b);
                    int d = (int)(Math.sqrt(N-a*a-b*b-c*c));
                    System.out.print(a+" ");
                    System.out.print(b+" ");
                    System.out.print(c+" ");
                    System.out.print(d+" ");
                    return;
                }
            }
        }
    }

}

关于这题的tips：（关于HashMap）

1. HashMap 是一个散列表，它存储的内容是键值对(key-value)映射。

2. HashMap 实现了 Map 接口，根据键的 HashCode 值存储数据，具有很快的访问速度，最多允许一条记录的键为 null，不支持线程同步。

3. HashMap 是无序的，即不会记录插入的顺序。

2016-Java省赛第九题——取球博弈

import java.util.Arrays;
import java.util.Scanner;

//取球博弈_递归_dfs(尝试、试探)
//优化：缓存，做记忆型递归
public class Main {
    
    private static int[] n; 
/*博弈问题：把球权交给对方之后，身份要互换*/
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        Scanner sc = new Scanner(System.in);
        n = new int[3];
        for (int i = 0; i < 3; i++) {
            n[i] = sc.nextInt();
        }
        Arrays.sort(n);//排序
        for (int i = 0; i < 5; i++) {
            int num = sc.nextInt();
            char res = f(num,0,0);
            System.out.print(res+" ");
        }
        System.out.println();
    }
    static char[][][] cache = new char[1000][2][2];
    /**
     * 参数代表着当前取球人面临的局面
     * @param num 球的总数
     * @param me 我方持有的数目-->我方数目的奇偶性
     * @param you 对手持有的数目-->对方数目的奇偶性
     * @return
     */
    private static char f(int num, int me, int you) {
        if(num=n[i]){
                char res = f(num-n[i],you,(n[i]&1)==0?me:(1-me));//注意此处，传递me和you的奇偶性
                if(res=='-') {
                    cache[num][me][you]='+';
                    return '+';
                }
                if(res=='0'){
                    ping = true;
                }
            }
        }
        //如果能走到这一行，说明不存在对手输的情况，那么是否存在平的情况？
        if(ping) {
            cache[num][me][you]='0';
            return '0';
        }
        else {
            cache[num][me][you]='-';
            return '-';
        }
    }

}

关于这题的tips：

递归+深搜+记忆型递归

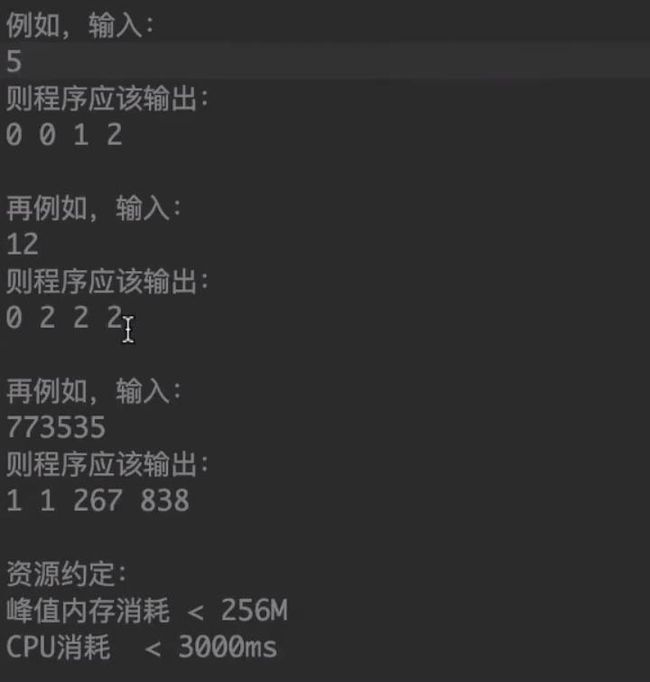
2016-Java省赛第十题——压缩变换

以下的代码由于数据规模的问题只能得30分：（暴力求解法）

import java.util.HashMap;
import java.util.HashSet;
import java.util.Map;
import java.util.Scanner;
import java.util.Set;

//压缩变换 
public class Main {
    static Map lastIndex = new HashMap();//数字与下标的映射
    static int[] data;//记录原始数据
    static int[] ans;//记录答案
    private static int n;
    
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        //处理输入
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        data = new int[n];
        ans = new int[n];
        for (int i = 0; i < n; i++) {
            int num = sc.nextInt();
            if(lastIndex.get(num)==null){//没出现过
                ans[i] = -num;
            }else{
                //统计p_num和i之间有多少不同的数字
                Set set = new HashSet();
                for (int j = lastIndex.get(num)+1; j < i; j++) {
                    set.add(data[j]);
                }
                ans[i] = set.size();
            }
            lastIndex.put(num, i);//更新
                
        }
        for (int i = 0; i < n; i++) {
            System.out.print(ans[i]+" ");
        }
        
    }

}

优化后：

import java.util.*;
//压缩变换
public class Main {
    static Map map = new HashMap();
    static int N;
    static int[] a; // 记录原始数据
    static int[] ans; // 记录变换后的结果
    static int[] b; // 这是一个0，1序列，b[i]为1当且仅当a[i]代表的数字最后一次出现的位置为i
                    // 最后求区间和的时候只要将b对应下标的值加起来即可
    static SegTree root; // 区间树

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        N = sc.nextInt();
        a = new int[N];
        b = new int[N];
        ans = new int[N];
        root = buildSegTree(0, N - 1); // 构造区间树

        for (int i = 0; i < a.length; i++) {
            int num = sc.nextInt();
            a[i] = num; // 将原数据保存起来
            Integer preIndex = map.get(num);
            // 如果是第一次发现该数
            if (preIndex == null) {
                ans[i] = -num;
                b[i] = 1;
            }
            // 如果不是第一次发现该数
            else {
                // 计算map.get(a[i])+1到i-1之间不同数字的个数==>求区间和
                ans[i] = query(root, preIndex + 1, i - 1);
                b[preIndex] = 0; // 更新上次出现位置为0
                b[i] = 1; // 更新本次出现位置为1
                // 更新之前位置的区间树
                update(root, preIndex, -1);
            }
            // 无论该key值是否第一次出现，将其put入map中
            map.put(a[i], i);
            // 更新i位置的区间树
            update(root, i, 1);
        }
        for (int i = 0; i < ans.length; i++) {
            System.out.print(ans[i] + " ");
        }
        sc.close();
    }

    // 计算b[p1]到b[p2]的和，通过区间树可以将其优化为log n的时间复杂度
    static int query(SegTree tree, int p1, int p2) {
        int l = tree.l;
        int r = tree.r;

        if (p1 <= l && p2 >= r) {
            return tree.sum;
        }
        if (p1 > p2) {
            return 0;
        }
        int mid = (l + r) / 2;
        int res = 0;
        if (p1 <= mid) {
            res += query(tree.lSon, p1, p2);
        }
        if (p2 > mid) {
            res += query(tree.rSon, p1, p2);
        }
        return res;
    }

    /**
     * b发生变化后，需要更新区间树
     * 
     * @param p
     *            改变的b的下标
     * @param num
     *            增量
     */
    static void update(SegTree tree, int p, int num) {
        // 递归出口
        if (tree == null) {
            return;
        }
        // 处理的当前SegTree
        tree.sum += num;
        // 递归处理子问题
        int l = tree.l;
        int r = tree.r;
        int mid = (l + r) >> 1;
        if (p <= mid) { // 左区间应该改变
            update(tree.lSon, p, num);
        } else {
            update(tree.rSon, p, num);
        }
    }

    // 区间树的数据结构
    static class SegTree {
        int l, r; // 左右区间的下标
        int sum; // 区间内的和
        SegTree lSon; // 左子树
        SegTree rSon;// 右子树

        public SegTree(int l, int r) {
            this.l = l;
            this.r = r;
        }
    }

    // 构建区间树
    static SegTree buildSegTree(int l, int r) {
        SegTree segTree = new SegTree(l, r);
        // 左右区间相同,叶子结点，sum为b[l]
        if (l == r) {
            segTree.sum = b[l];
            return segTree;
        }
        // 左右区间不同
        int mid = (l + r) / 2;
        SegTree lson = buildSegTree(l, mid);
        SegTree rson = buildSegTree(mid + 1, r);
        segTree.lSon = lson;
        segTree.rSon = rson;
        segTree.sum = lson.sum + rson.sum;
        return segTree;
    }
}

关于这题的tips：

这里用到了区间树，详细的可以看视频理解。

总结

程序填空题（填结果）

01：煤球数目 找规律简单计算

02：生日蜡烛 枚举:1.两个年龄2.过生日的次数，等差数列求和的公式

03 ：凑算式 全排列+check

程序填空题（填代码）

04：分小组 逻辑

05：抽签 递归，搞清楚参数的含义和参数的变化方向

程序填空题（填结果）

06：方格填数 全排列+check

07：剪邮票 全排列（带重复元素的全排列，要用套路全排套路1) +标注（二维数组上标注01) +dfs求连通块数目

编程题

08：四平方和 枚举优化(hash缓存)

09：取球博弈 典型的博弈框架（带平局)

10：压缩变换 hash查找+标注（一维数组上标注01便于区间求和)+区间树（线段树)

---

2016年用到了三次全排列，由此可见全排列的模板一定要记住！后面几题还是有难度的，需要多做题，多琢磨。