回溯算法 一个公式就够了
目录
两个万能模板
1.子集
2.子集 II
3.组合
4.组合总和
5.组合总和 II
6.全排列
7.全排列 II
8.字符串的全排列
9.字母大小写全排列
两个万能模板
- 方法一 相对顺序不变
从左往右走 start 控制层数
vector> vv;
vector v;
dfs(vector& nums, int start)
{
if(start == nums.size())
{
vv.push_back(v);
return;
}
v.push_back(nums[start]);
dfs(nums, start+1);
v.pop_back();
dfs(nums, start+1);
}
- 方法二 相对顺序不变 (搭配 vector
visit 可以解决相对顺序改变问题)
start 控制层数 (根据题目要求 , 用需要的条件来控制何时返回)
vector> vv;
vector v;
dfs(vector& nums, int start)
{
if(start == nums.size())
{
vv.push_back(v);
return;
}
for (int i = start; i < nums.size(); ++i) // 这是每个数只能取一次的情况
{
v.push_back(nums[i]);
dfs(nums, i+1);
v.pop_back();
}
}
上面两个模板看懂了,我们可以开始刷题了. (不懂 可以 画个递归图来理解)
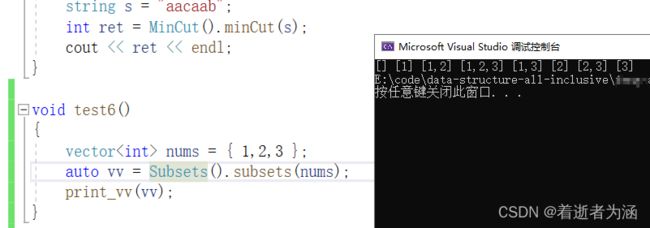
1.子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[ [] , [1] , [2] , [1,2] , [3] , [1,3] , [2,3] , [1,2,3] ]
使用方法一 完美解决
class Solution {
public:
vector v; // 单个子集
vector> vv; // 子集集合
void dfs(int cur, vector& nums) { // cur:当前搜索的数组位置
if (cur == nums.size()) { // 递归下界
vv.push_back(v); // 保存这一趟的结果
return;
}
v.push_back(nums[cur]); // 加入当前元素
dfs(cur + 1, nums); // 进入下一状态
v.pop_back(); // 回溯,回退到未加入当前元素的状态
dfs(cur + 1, nums); // 进入下一状态
}
vector> subsets(vector& nums) {
dfs(0, nums);
return vv;
}
}; 现在简单分析下代码递推过程:
v 深度优先遍历 -- [] [1] [1,2] [1,2,3] cur值变为3 vv.push_back(v) return
cur 值回退到2 v.pop -- [1,2] 递归下一层 cur = 3 [1,2] 入vv return
cur 值回退到2 函数结束 cur回退到1 v.pop -- [1] 递归下一层 cur = 2
v.push_back(nums[2]) -- [1,3] cur = 3 vv.push_back(v) return ......
有点麻烦就不模拟了 , 后面过程完全一样 最终结果如下
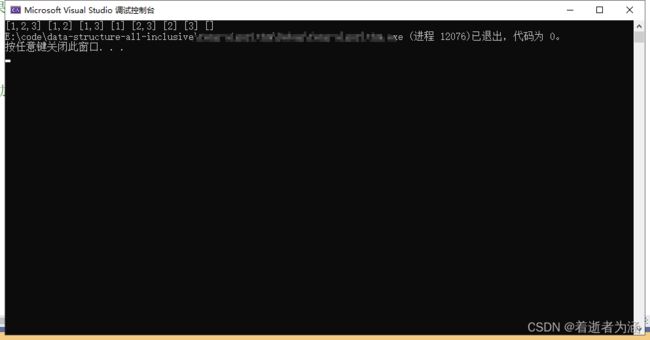
[1,2,3] [1,2] [1,3] [1] [2,3] [2] [3] []
方法二这里能使用吗 完全可以 我们使用了 i = start 控制它 不会出现 [2,1,3] 这种情况
class Subsets
{
public:
vector> vv;
vector v;
void dfs(vector& nums, int start)
{
vv.push_back(v); // 收破烂的 , 来者不拒
for (int i = start; i < nums.size(); ++i)
{
v.push_back(nums[i]);
dfs(nums, i + 1);
v.pop_back();
}
}
vector> subsets(vector& nums) {
dfs(nums, 0);
return vv;
}
}; v 是以什么顺序入 vv 的呢?
[ ] [1] [1,2] [1,2,3] start = 3 now 直接 返回 start=2 v.pop [1,2] i = 2 结束 i++ i = 3 返回 start=2 这层结束 start = 1 pop v = [1] i = 1 结束 i = 2 push [1,3] start = 3 (i+1 = 3) ...
[] [1] [1,2] [1,2,3] [1,3] [2] [2,3] [3] 头脑风暴了一下,顺序应该是这样,程序检验:
2.子集 II
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
输入:nums = [1,2,2] 输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
- 对数组进行排序
- 去重 (vector
vis)
确定用哪种模板 --- for 循环版本更容易控制一些
i > 0 && nums[i] == nums[i - 1] && visit[i-1]==false
关键控制步骤在这 1 2 2 第一个2 没有进去的话 第二个2也不用进了,不然会重复
class Solution {
public:
vector v;
vector> vv;
vector visit;
void dfs(vector& nums, int start)
{
vv.push_back(v);
for (int i = start; i < nums.size(); ++i)
{
if (i > 0 && nums[i] == nums[i - 1] && visit[i-1]==false)
continue;
v.push_back(nums[i]);
visit[i] = true;
dfs(nums, i + 1);
v.pop_back();
visit[i] = false;
}
}
vector> subsetsWithDup(vector& nums) {
sort(nums.begin(), nums.end());
visit.resize(nums.size());
dfs(nums, 0);
return vv;
} 3.组合
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
输入:n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]
很简单,方法一 二都可以
class Solution{
public:
vector> vv;
vector v;
void dfs(int start, int n, int k)
{
if (v.size() == k)
{
vv.push_back(v);
return;
}
for (int i = start; i < n; ++i)
{
v.push_back(i + 1);
dfs(i + 1, n, k);
v.pop_back();
}
}
vector> combine(int n, int k) {
dfs(0, n, k);
return vv;
}
}; class Solution2 {
public:
vector> vv;
vector v;
void dfs(int start, int n, int k)
{
if (v.size() == k)
{
vv.push_back(v);
return;
}
if (start == n + 1)return;
v.push_back(start);
dfs(start + 1, n, k);
v.pop_back();
dfs(start + 1, n, k);
}
vector> combine2(int n, int k) {
dfs(1, n, k);
return vv;
}
}; 4.组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合
- 可以无限次数使用 start 不再用来控制终止条件 要用sum来控制
- for循环 要 i = 0 开始 保证每个位置可以取多次
但使用这种方法 有个问题 没办法去重--- [2,2,3] [2,3,2] [3,2,2] 均会被push进去
使用方法一
以下是错误版本!!! (解决方法也有,再加个start i=start控制它往右找数)
calss Solution{
public:
vector> vv;
vector v;
void dfs(vector& candidates, int target, int sum)
{
if (sum == target)
{
vv.push_back(v);
return;
}
else if (sum > target)return;
for (int i = 0; i < candidates.size(); ++i)
{
v.push_back(candidates[i]);
dfs(candidates, target, sum + candidates[i]);
v.pop_back();
}
//怎么控制它只往右找呢 // 非for循环版可以很好解决这个文体
}
vector> combinationSum2(vector& candidates, int target) {
int sum = 0;
//sort(candidates.begin(),candidates.end());
dfs(candidates, target, sum);
return vv;
}
}; 正确版本!!! start 必须 **进厂** 了
start不在控制递归层数 它用来判断是否越界
class CombinationSum {
public:
vector> vv;
vector v;
void dfs(vector& candidates, int target, int sum, int start)
{
if (sum == target)
{
vv.push_back(v);
return;
}
else if (sum > target || start==candidates.size())
return;
v.push_back(candidates[start]);
dfs(candidates, target, sum + candidates[start], start);//递归自己
v.pop_back();
dfs(candidates, target, sum, start + 1);//递归下一位
}
vector> combinationSum(vector& candidates, int target) {
int sum = 0;
dfs(candidates, target, sum, 0);
return vv;
}
}; 5.组合总和 II
给你一个由候选元素组成的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个元素在每个组合中只能使用 一次 。
- 每个数只能用一次 + 包含重复数组
老规矩: vis + 两个判断解决这个问题
class Solution {
public:
vector> vv;
vector v;
vector vis;
void dfs(vector& candidates,int target, int sum, int start)
{
//一个数只能用一次好说 双递归 -> 组合 ||| for 循环 -> 排列
if (sum == target)
{
vv.push_back(v);
return;
}
if (sum > target || start >= candidates.size())return;
if(start>0 && candidates[start]==candidates[start-1] && vis[start-1]==false)//[1,1,6] [1,2,5] [1,7] [2,6]
{
dfs(candidates, target, sum, start + 1);
}
else
{
vis[start] = true;
v.push_back(candidates[start]);
dfs(candidates, target, sum + candidates[start], start + 1);
vis[start] = false;
v.pop_back();
dfs(candidates, target, sum, start + 1);
}
}
vector> combinationSum2(vector& candidates, int target) {
sort(candidates.begin(), candidates.end());
vis.resize(candidates.size());
dfs(candidates, target, 0, 0);
return vv;
}
}; 6.全排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
官方给的是经典的swap方法 但我们只会上面两种模板 那就继续用上面的方法解决这种问题
- 每次从零开始检测 哪个数还没有访问过 访问到的标记true 回溯时标回false
class Solution {
vector> vv;
vector v;
vector vis;
public:
void dfs(vector& nums, int start)
{
if (start == nums.size())
{
vv.push_back(v);
return;
}
for (int i = 0; i < nums.size(); ++i)
{
if (vis[i] == true)continue;
v.push_back(nums[i]);
vis[i] = true;
dfs(nums, start+1);
v.pop_back();
vis[i] = false;
}
}
vector> permute(vector& nums) {
vis.resize(nums.size());
dfs(nums, 0);
return vv;
}
}; 官方提供的解法:
class Solution {
public:
void dfs(vector>& vv, vector& nums, int first, int len)
{
if(first == len)
{
vv.push_back(nums);
return;
}
for(int i=first; i> permute(vector& nums) {
vector> vv;
dfs(vv, nums, 0, nums.size());
return vv;
}
}; 7.全排列 II
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
- 先排序 再设置条件去重
- vis[i] == true || (i>0 && nums[i]==nums[i-1] && vis[i-1]==false
class Solution {
public:
vector> vv;
vector v;
vector vis;
void dfs(vector& nums, int start)
{
if (start == nums.size())
{
vv.push_back(v);
return;
}
for (int i = 0; i < nums.size(); ++i)
{
if (vis[i] == true || (i>0 && nums[i]==nums[i-1] && vis[i-1]==false))continue;
v.push_back(nums[i]);
vis[i] = true;
dfs(nums, start + 1);
v.pop_back();
vis[i] = false;
}
}
vector> permuteUnique(vector& nums) {
vis.resize(nums.size());
sort(nums.begin(), nums.end());
dfs(nums, 0);
return vv;
}
}; 8.字符串的全排列
去重方法和前面的一模一样 不在敖述
另外本体可以优化 , 字符串递归直接:
优化前 str.append(1,s[i]);
vis[i] = true;
dfs(s, start + 1);
str = str.substr(0,str.length()-1);
优化后 dfs(s+s[i], start + 1);
为了强行匹配模板,写成了上面的模样class Solution {
public:
vector vs;
vector vis;
string str;
void dfs(string& s, int start)
{
if (start == s.length())
{
vs.push_back(str);
return;
}
for (int i = 0; i < s.length(); ++i)
{
if (vis[i] == true || (i>0 && s[i]==s[i-1]&&vis[i-1]==false))continue;
str.append(1,s[i]); // 没办法 没有重载 append (char) 只能 fill 功能 append(n,char)
vis[i] = true;
dfs(s, start + 1);
//str.erase(str.length()-1,string::npos);//第一个默认0 第二个默认 -1 npos
str = str.substr(0,str.length()-1);
vis[i] = false;
}
}
vector permutation(string s) {
vis.resize(s.length());
sort(s.begin(), s.end());
dfs(s, 0);
return vs;
}
}; 9.字母大小写全排列
给定一个字符串S,通过将字符串S中的每个字母转变大小写,我们可以获得一个新的字符串。返回所有可能得到的字符串集合。
经过上面的训练,相信这道题已经是very easy
class Solution {
public:
vector vs;
void dfs(string& s, int start)
{
if (start == s.length())
{
vs.push_back(s);
return;
}
if (isalpha(s[start]))
{
//爱与不爱算法
s[start] = toupper(s[start]);
dfs(s, start + 1);
s[start] = tolower(s[start]);
dfs(s, start + 1);
}
else
dfs(s, start + 1);
}
vector letterCasePermutation(string s) {
dfs(s, 0);
return vs;
}
}; 先到这里吧 , 有空再整理动态规划,贪心算法,搜索算法
搜索算法还是很有趣的...
2022/1/6