深度学习 | CNN卷积核与通道

 

10.1、单通道卷积

以单通道卷积为例，输入为（1,5,5），分别表示1个通道，宽为5，高为5。

假设卷积核大小为3x3，padding=0，stride=1。 

运算过程：

        

不断的在图像上进行遍历，最后得到3x3的卷积结果，结果如下： 

        

---

---

10.2、多通道卷积

以彩色图像为例，包含三个通道，分别表示RGB三原色的像素值

输入为（3,5,5），分别表示3个通道，每个通道的宽为5，高为5。

假设卷积核只有1个，卷积核通道为3，每个通道的卷积核大小仍为3x3，padding=0，stride=1。

每一个通道配一个卷积核

每一个通道的像素值与对应的卷积核通道的数值进行卷积，因此每一个通道会对应一个输出卷积结果，三个卷积结果对应位置累加求和，得到最终的卷积结果（这里卷积输出结果通道只有1个，因为卷积核只有1个。卷积多输出通道下面会继续讲到）。

可以这么理解：最终得到的卷积结果是原始图像各个通道上的综合信息结果。

        

我们把上述图像通道如果放在一块，计算原理过程还是与上面一样，堆叠后的表示如下：

        

在上面的多通道卷积1中，输出的卷积结果只有1个通道，把整个卷积的整个过程抽象表示，

过程如下：

        

由于只有一个卷积核，因此卷积后只输出单通道的卷积结果

（黄色的块状部分表示一个卷积核，黄色块状是由三个通道堆叠在一起表示的，每一个黄色通道与输入卷积通道分别进行卷积，也就是channel数量要保持一致，图片组这里只是堆叠放在一起表示而已

那么，如果要卷积后也输出多通道，增加卷积核（filers）的数量即可，示意图如下

        

备注：上面的feature map的颜色，只是为了表示不同的卷积核对应的输出通道结果，不是表示对应的输出颜色。

然后将每个卷积核对应的输出通道结果（feature map）进行拼接，图中共有m个卷积核，则输出大小变为（m*w'*h'），其中w'、h'表示卷积后的通道尺寸，原始输入大小为（n*w*h）。

因此整个卷积层的尺寸为（m*n*k1*k2）是一个4维张量，其中m表示卷积核的数量，n表示通道数量，k1表示每一个卷积核通道的宽，k2表示每一个卷积核通道的高。

即：

        卷积核通道数量 = 输入通道数量

        输出通道数量 = 卷积核个数

---

---

10.3、代码输出

•  pytorch所有的输入必须是小批量的,图像虽然是nxmxh的，但是必须要加batch
• randn从正态分布采样的随机数
• kernel_size可以是常数（一般是奇数），也可以传入元组如(5,3)

import torch
 
in_channels = 5  #输入通道数量
out_channels =10 #输出通道数量
width = 100      #图像大小
height = 100     #图像大小
kernel_size = 3  #卷积核尺寸
batch_size = 1   #批数量
 
input = torch.randn(batch_size,in_channels,width,height)
conv_layer = torch.nn.Conv2d(in_channels,out_channels,kernel_size=kernel_size)
 
out_put = conv_layer(input)
 
print(input.shape)
print(out_put.shape)
print(conv_layer.weight.shape)

 

• 输入：5个通道100x100
• 输出：10个通道 98x98
• 卷积层权重形状 mxnxw'xh'
• （1）输入的张量信息为[1,5,100,100]分别表示batch_size，in_channels，width，height
• （2）输出的张量信息为[1,10,100,100]分别表示batch_size，out_channels，width'，height'，其中width'，height'表示卷积后的每个通道的新尺寸大小
• （3）conv_layer.weight.shape的输出结果为[10, 5, 3, 3]，分表表示

 

---

---

10.4、初始化常见参数

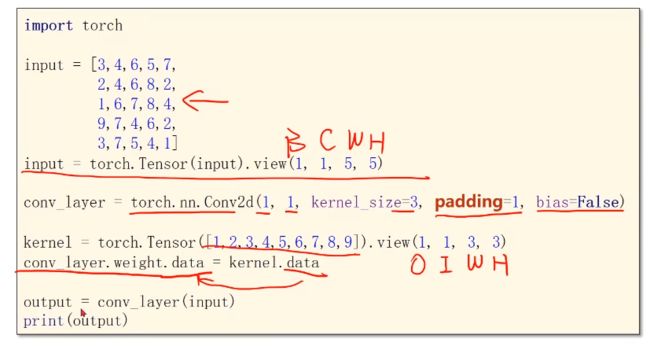
padding 填充 —— 若我们希望output大小不变

• kernel/2 = 填充几圈
• 
• 

代码举例实现：

        

---

stride 步长 —— 降低图像宽度和高度

• 本例中 stride = 2
• 
• 
• 

---

下采样

Max Pooling Layer 最大池化层

• 通道数量不变，图像大小发生改变
• 若使用2x2的Maxpooling 默认stride = 2
• 

代码实现：

        

---

部分文字参考于

【Pytorch深度学习实践】B站up刘二大人之BasicCNN & Advanced CNN -代码理解与实现(9/9)_b站讲神经网络的up土堆-CSDN博客

CNN卷积核与通道讲解 - 知乎

视频讲解及图片来源

10.卷积神经网络（基础篇）_哔哩哔哩_bilibili