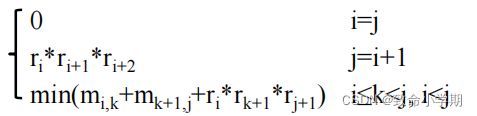最优解:data[1][1] -> data[2][j] -> data[i+1][j]->....., i=j=1,j=j+path
最优值 r[1][1]
子集合最优的决策和记录路径

| 算法设计与描述 |
算法分析 |
| 输入:数塔data[n][n] |
(1) |
| 输出:结点权值最大路径,及其值 |
|
| void datatower(int data[][N], int n)
{
int r[n][N] = { 0 };
int i, j;
int path[n][N] = { 0 }; //先是最底层 也就是第一层的数,直接赋值给
for (i = 1; i < n; i++)
{
r[n - 1][i] = data[n - 1][i];
} //第二层到最后一层,也是阶段
for (i = n - 2; i > 0; i--)//阶段
{ //现阶段最优值计算
for (j = 1; j <= i; j++)//子集合
{
if (r[i + 1][j] > r[i + 1][j + 1])//垂直下方 > 右下方
{
r[i][j] = r[i + 1][j + 1] + data[i][j];
path[i][j] = 0;
}
else
{
r[i][j] = r[i + 1][j + 1] + data[i][j];
path[i][j] = 1;
}
}
}
//输出权值最大的路径,及最大权值
j = 1;
cout << "max value of the tower is %" << r[1][1] << endl;
for (i = 1; i < n - 1; i++)
{
cout << data[i][j] << "->";
j = j + path[i][j];
}
cout << data[i][j]; } |
|
代码:
#include
using namespace std;
//数塔
//原结点
int const n=5+1;
int data[n][n]={{0},{0,8},{0,11,14},{0,10,5,8},{0,3,17,9,4},
{0,18,7,12,6,16}};
void show(int a[][n])
{
for(int i=1;i0;i--)//逐层向上
{
for(int j=1;j<=i;j++)//当前层,也就是当前阶段的最优解计算
{
if(r[i+1][j]>r[i+1][j+1])
//当前层的下一层 类似于左右子节点进行比较
//选择较大的
{
r[i][j]=r[i+1][j]+data[i][j];
path[i][j]=0;//选择左节点
}
else
{
r[i][j]=r[i+1][j+1]+data[i][j];
path[i][j]=1;//选择左节点
}
}
}
//输出权值最大的路径及最大权值
cout<<"max :"<";
j=j+path[i][j];
}
cout<<"["<[2,1]11-->[3,1]10-->[4,2]17-->[5,3]12
*/
//优化 一维数组暂存数据
#include
using namespace std;
//数塔
//原结点
int const n=5+1;
int data[n][n]={{0},{0,8},{0,11,14},{0,10,5,8},{0,3,17,9,4},
{0,18,7,12,6,16}};
void tower(int data[][n])
{
int i,j;
int r[n];//存每一行的数据
//每一次实际上都是比较刷新后的底层数据(加和之后)
//因此可以用一维数组进行存储
//这种比较是破坏性的 ,只需要最新的数据
int col[n][n]={0};
//这个不能用一维数组代替,因为
//最后是从顶向下进行找列坐标 ,然而比较是从底向上
//因此需要之前的数据
//差不多这个意思
//最底层的数据
for(i=0;i0;i--)
{
for(j=1;j<=i;j++)
{
//比较左右子结点
if(r[j]>r[j+1])
{
r[j]=r[j]+data[i][j];
//左结点大 记录左节点 用数据记录
col[i][j]=0;//第i层的选择
}
else//右结点大 记录右结点
{
r[j]=r[j+1]+data[i][j];
col[i][j]=1;//第i层的选择
}
}
}
//结束
cout<<"max:"<";
j=j+col[i][j];
}
}
int main()
{
tower(data);
return 0;
}
投资分配问题
【例8-2】设有n万元钱,投资m个项目,将x i 万元钱投入第i个项产生的效益为f i (x i ),i=1,2,…,m。请问如何分配这n万元钱,
使得投资的总效益最高?
问题分析
依题意,可以列出该问题的方程:

5万元有三种分配情况:
①全部投资给某一个项目;
②按比例投资给任意两个项;
③按比例投资给三个项目
第一阶段,给项目1投资,列出项目1投资的最优投资方案,
其获利方程可表示为 g 1 (x)= f 1 (x i ),x i =0,1,2,3,4,5
计算模型
(1) 递推方程
设k为阶段变量,0≤k≤m由问题分析可得递推方程和边界条件:
(2)存储 设有m个项目,共投资n万元。最多m个阶段。
a[][]表示某阶段最大获利情况下分配给某个项目资金。a[i][j]?前i项目一共j万元,值是给第i个项目的资金 // i是阶段,也是第i 个项目, j是前i个投资的最大,值是给第i个项目的
f[]存储某项目初始投资所获得利润。f[i]表示投资i万元给某项 目所获得的利润(数组值)。
t[]存储当前投资额的最大利润
g[]存储每一阶段的最优方案。运算完毕后,更新g[k]=t[k]。
gain[]存储整个投资的最优分配方案。
(3)求解最优方案
a[m][n]就表示投资n万元,得到最大获利后,分配项目m的资金。
设rest=n,令gain[m]=a[m][rest]表示最后一个项目在最优分配方案中的最大配额。
rest=rest – a[m][n] //减去给第i项目的投资
a[m-1][rest]就表示给第m-1个项目分配rest取得最大利润后,分配给第m-1个项目资金。
rest=rest – a[m-1][rest]表示减去最后两个项目后的投资,则a[m-2][rest]就表示给第m-2个项目分配rest取得最大利润后,分配给第m-2个项目资金。
依此类推,……就可以找到最优解
代码:
#include
using namespace std;
void output(int a[])
{
for(int i=0;i<100;i++)
{
// if(a[i]!=0)
cout<>f[j];//第一组收益
f[j]=temp[0][j];
g[j]=f[j];//第一阶段
a[1][j]=j;//第一阶段最优配额
}
for(k=2;k<=m;k++)//从第2个项目开始的各个收益
{
for(i=0;i<=n;i++)
{
t[i]=f[i];//保存上一个的值
// cin>>f[i];//当前项目投入i万元的收益
f[i]=temp[k-1][i];
a[k][i]=0;
}
//k个项目 总共投资i万元
for(i=0;i<=n;i++)
{
for(j=0;j<=i;j++)//投资从0到i万元
{
//共投资i万元
//如果投资项目k j万元+投资其他(其他默认是最优)i-j万元,
//> t[i]投资i
if(f[j]+g[i-j]>t[i])//计算当前最优值
{
t[i]=f[j]+g[i-j];
// cout<0;i--)//从第m个项目到第1个项目 遍历所有项目
{
gain[i]=a[i][rest];
rest=rest-gain[i];
}
// output(gain);
cout<<"最优方案:"<
背包问题
【例8-2】背包问题(Knapsack Problem)。
给定n个重量为w 1 , w 2 ,…w n ,价值为v 1 , v 2 ,…v n 的物品和一个承重为W的背包,
求 将这些物品中的某些装入背包中,在不超出重量W的情况下,价值最高的装法。
背包问题属于 线性规划问题。如果线性规划问题的变量都是非负整数,则称为 整数规划问题。背包问题就是整数规划问题。限制所有的x i =0或x i =1时的背包问题称为 0-1背包问题。
最优子结构的证明——整体最优解包含局部最优解
设(y1,y2,...,yn)是所给0-1背包问题的一个最优解,
去掉 y1,有
则 (y2,...,yn)是(2)式的一个最优解。
【这就是最优子结构】
如果不成立,设(z2,...zn)是(2)的一个最优解,则有
此时


矛盾,得证。
非等分子问题 =》 等差递增问题 =》拆包 (背包的承载量进行等分)
背包的限重为 w ( w ≤W),求前i(1≤i≤n)个物品装包的最优解。
设前i-1个物品装包的最优值为 f i-1 ( w ),则有两种情况:
装入i物品和不装入i物品,则有
f i ( w )=max{ f i-1 ( w ), f i-1 ( w-w i )+ v i }。//如果不装,就是上一次的最优值;如果装,就是
当w i>w时,f i ( w )= f i-1 ( w)
当背包没有装入物品时,最优价值为0;
当背包承载为0时,不能装入物品,最优价值也为0。
子集合及阶段划分:
(1) 将每加入一个物品看成一个阶段。
(2) 将背包的承重划分为不同的重量。
计算模型
(1)递推方程
(2)存储
i—表示物品编号,j表示背包当前的限载重量
W—表示背包最大承载重量
w[]—表示物品重量,如第i个物品的重量为w[i]
v[]—表示物品价值,如第i个物品的价值为v[i]
f[][]—表示在某限载情况下,背包最优装载的价值,
如f[i][j]指在背包限载重量为j的情况下,第i阶段(前i个物品)最优装载的价值。
例子:

第1阶段,新增物品i=1,有
f1(1)= f0 (1)=0;//限重为1,小于w[1] (w[1]=2)
f1 (2)= max{ f0(2), f0 (2-w[1])+v[1]}= max{0, f0 (0)+12}=12;
f1 (3)= max{ f0 (3), f0 (3-w[1])+v[1]}= max{0, f0 (1)+12}=12;
同理有f1 (4)= 12; f1 (5)= 12;
第2阶段,新增物品i=2,有
f2(1)= max{ f1 (1), f1 (1-w[2])+v[2]}= max{0, f1 (0)+10}={0,10}=10;
f2 (2)= max{ f1 (2), f1 (2-w[2])+v[2]}= max{12, f1 (1)+10}={12,10}=12;
f2 (3)= max{ f1 (3), f1 (3-w[2])+v[2]}= max{12, f1 (2)+10}={12,22}=22;
同理有f1 (4)= 22; f1 (5)= 22;
第3阶段,新增物品i=3,有
f3(1)= f2 (1)=10 ; //限重为1,小于w[3] (w[3]=3)
f3 (2)= f2 (2)=12 ; //限重为2,小于w[3] (w[3]=3)
f3 (3)= max{ f2 (3), f2 (3-w[3])+v[3]}= max{22, f2 (0)+20}={22,20}=22;
f3 (4)= max{ f2 (4), f2 (4-w[3])+v[3]}= max{22, f2 (1)+20}={22,30}=30;
f3 (5)= max{
f2 (5), f2 (5-w[3])+v[3]}= max{22, f2 (2)+20}={22,32}=32;
复杂度分析
(1)问题的输入规模是n个重量w[n],n个价值v[n]及背包总承载重量W
(2)第1阶段动态规划前后两部分合起来的初始化是W次
除去第1阶段动态规划外,还有n-1阶段动态规划,其中均
包含W次优化过程,可以表示如下:
(3)回溯推导最优解所需要的计算次数为n次。
总综上所述,可得
T(n)=W+(n-1)(W+1)+n=n*W+2*n-1=θ(n*W)

【例8-3】矩阵连乘问题
内在规律:
1.保证可以连乘:列=行
2.运算次数:
【例8-3】矩阵连乘问题。
设M 1 , M 2 ,…M n为n个矩阵的序列, 其中M i 为r i ×r i+1阶矩阵,i=1,2, …,n。
这个矩阵链的输入是向量R= 0 ,r 1 , …,r n >,因为矩阵运算满足结合律,所以运算结果
与计算的顺序无关,但是不同运算顺序,会造成运算时的乘法
次数的不同。求以哪种乘法次序运算,使得基本运算的总次数最少。
问题分析
例: M1[5*20] * M2[20*50] * M3[50*1] * M4[1*100]
可能的运算次序为:
C[((M1*M2)*M3)*M4]=5*20*50+5*50*1+5*1*100=5750
C[M1*(M2*(M3*M4))]=50*1*100+20*50*100+5*20*100=115000
C[(M1*(M2*M3))*M4]=20*50*1+5*20*1+5*1*100=1600
运算次数提高非常明显,需要找到这些分割点
(1)阶段划分:按矩阵多少进行划分
第1阶段 :一个矩阵相乘的计算量为0;
第2阶段 :计算两个相邻矩阵相乘的计算量, 共3组 【只是计算,没有判优判劣】
第3阶段 :计算两个相邻矩阵相乘的结果与第三个矩阵相乘的计算量, 共2组 【决策优势】
第4阶段 :计算三个矩阵相乘的结果与第四个矩阵相乘的计算量, 共1组 【矩阵越多,分割点的选择越多,有优劣区别。不适合贪心:前集合和后集合有重合部分】
(2)阶段决策:有备忘的算法,影响:起点,终点,矩阵数目——跨度。为了找到分界点
设矩阵大小为:M 1 为r 1 ×r 2 , M 2 为r 2 ×r 3 , M 3 为r 3 ×r 4 , M 4 为r 4 ×r 5
• 1个矩阵“相乘”有4种情况
m 11 =0; m 22 =0; m 33 =0; m 44 =0;
• 2个矩阵相乘有3种情况:
m 12 =r1 *r 2 *r 3 ; m 23 =r2 *r 3 *r 4 ; m 34 =r 3 *r 4 *r 5 ;
• 3个矩阵连续相乘有
2种情况:
m 13 =min{m 12 +m 33 +r 1 *r 3 *r 4 ,m 11上阶段的增益 +m 23 +r 1 *r 2 *r 4本阶段增益 }
m 24 =min{m 23 +m 44 +r 2 *r 4 *r 5 ,m 22 +m 34 +r 2 *r 3 *r 5 }
• 4个矩阵相乘矩阵有1种情况:
m 14 =min{m 11 +m 24 +r 1 *r 2 *r 5 ,m 12 +m 34 +r 1 *r 3 *r 5 ,m 13 +m 44 +r 1 *r 4 *r 5 }
数学模型
设求n个矩阵连乘基本运算次数为C[M 1 *M 2 *M 3 *……*M n ],
其中, M i 为r i *r i+1 阶矩阵,i=1,2,3,…, n。
设m i,j 是计算M i *M i+1 *…M j的最少乘法次数(1≤i≤j≤n),对m i,j 有公式:
因为有i≤j,所以,可设 j=i+s, s=0,1,…,n-1, 则有m i,j =m i,i+s 。
记录最优解
用二维矩阵com ij(n*n) 来存储使m ij 为最小值时的 k 值

思考题:如何还原最优解?
算法设计与描述
(1)递归算法
(主函数)

代码://递归
#include
using namespace std;
int n=4;
int r[100]={0,5,20,50,1,100};//保存矩阵大小
int com[100][100]={0};//保存矩阵编号
int temp[100][100];//保存Mij最优计算量
int cou(int i,int j)
{
cout<"<=0)//已经计算过
{
//因为是从小到大,所以没有覆盖
return temp[i][j];
}
if(i==j)//此时 Mii 也就是同一个矩阵
{
temp[i][j]=0;//所需计算量为0
// com[i][j]=0;//此时分割点,已经在初始化时赋值了
return temp[i][j];
}
if(i+1==j)//两个矩阵相乘 结果固定
{
temp[i][j]=r[i]*r[i+1]*r[i+2];
com[i][j]=i;//此时分割点的下标 是i
return temp[i][j];
}
//其他情况 此时有多个情况
//其中一个选择,作为基准值
int x=cou(i,i)+cou(i+1,j)+r[i]*r[i+1]*r[j+1];//0增益+已知增益+新增增益
com[i][j]=i;//记录这种分割点
int y;
for(int k=i+1;k
代码:非递归
//非递归
void fei()
{
int n=4;
int r[10]={0,5,20,50,1,100};//Mi 是矩阵ri*ri+1
int com[10][10]={0};//保存矩阵编号
int m[10][10]={0};//m[i][j]是Mi***Mj的最小乘法次数
for(int i=1;i<=n;i++)//M1 -- M4
{
m[i][i]=0;//一个矩阵
m[i][i+1]=r[i]*r[i+1]*r[i+2];//两个矩阵相乘 M1 M2
com[i][i+1]=i;//分割点是i
}
//三及以上个矩阵 Mij
for(int j=1;j<=n;j++)
// for(int i=2;i<=n;i++)//一共i个矩阵
{
for(int i=2;i<=n;i++)
// for(int j=1;j<=n;j++)
{
if(i+j-1>n)continue;
//Mj Mj+1 M..Mj+i-1
//此时Mj开始 一共i(3->n)个矩阵 前i-1个矩阵已经乘完 因此间隔点应是[j+i-2] Mj...Mj+i-2*Mj+i-1
//Mj j+i-1
m[j][j+i-1]=m[j][j]+m[j+1][j+i-1]+r[j]*r[j+1]*r[j+i];
com[j][j+i-1]=i;
// m[j][j+i-1]=m[j][j+i-1]+r[j]*r[j+i-1]*r[j+i];
// com[j][j+i-1]=j+i-2;//间隔点
int temp;
for(int k=j+1;k<=j+i-1;k++)//间隔点 下标
{
temp=m[j][k]+m[k+1][j+i-1]+r[j]*r[k+1]*r[j+i];
if(temp
思考题:

1.证明具有最优子结构:
问题分析:
机器数n=5,厂子数m=3,将xi台机器给第i个厂子 效益为fi(xi) ,i=1...m
目标方程 max sum[ fi(xi)] i=1...m
s.t. sum[ xi ]=n 台机器 xi∈n xi>=0 i=1..m厂子
第一阶段:给A厂投资,g1(x)=f1(xi)
第二阶段:加入B厂,g2(x)=max{ f2(xi)+g1(x-xi) }
第三阶段:加入C厂,g3(xi)=
总结:
代码:
#include
using namespace std;
void invest()
{
int n=5;//机器
int m=3;//厂子
int profit[10][10]={{0},{3,5,4},{7,10,6},{9,11,11},{12,11,12},{13,11,12}};
// fit[i][j] i台机器对厂子j的盈利
int machine[10][10]={0};//最大利益时,一共i台机器 给j厂machine[i][j]台
int tempinitprofit[10];//当前阶段最大利益
int tempmaxprofit[10];
int tempplan[10]={0};//当前阶段最优计划
int maxmachine[10];//最终计划
//一台厂子时
for(int i=0;i<=n;i++)
{
tempinitprofit[i]=profit[i][0];
tempmaxprofit[i]=profit[i][0];
machine[1][i]=i;
}
for(int k=2;k<=m;k++)
{
//加入厂子k
//初始化
for(int i=0;i<=n;i++)
{
tempinitprofit[i]=tempmaxprofit[i];//实际是上一阶段的最大利润
tempmaxprofit[i]=profit[i][k-1];
machine[k][i]=0;
// cout<tempplan[i])
{
tempplan[i]=tempmaxprofit[j]+tempinitprofit[i-j];
// cout<0;i--)
{
maxmachine[i]=machine[i][rest];
rest=rest-maxmachine[i];
}
//输出
cout<<"最佳方案:"<
![]()