哈希表（C语言）

哈希表

​ 哈希表又称散列表，是一种是“key-value"形式存储的数据结构。即将key映射到表上的一个单元，从而实现快速查找等操作，这个映射操作就叫散列，具体通过散列函数实现相应的映射。根据key的形式，散列的形式多种多样，这里以正整数为例，常用的散列函数为：
$$Hash(Key)=Key\%TableSize$$
​ TableSize为表长，一般情况下，我们希望一个元素能唯一对应表上的一个单元，但是这是不可能的，一定会存在不同的Key映射到相同单元的情况，这就称为冲突，因此我们需要想办法解决冲突。首先，保证表长为素数可以一定程度减少冲突，使关键字的分配更均匀。最后，介绍两种常用的冲突解决方法，分离链接法（拉链法）和开放定址法。

分离链接法

​ 分离链接法使用链表结构解决冲突，首先分配一个链表数组，当相应位置出现冲突时，创建一个新的哈希节点接在后面，看起来就像拉链一样。

相关例题：

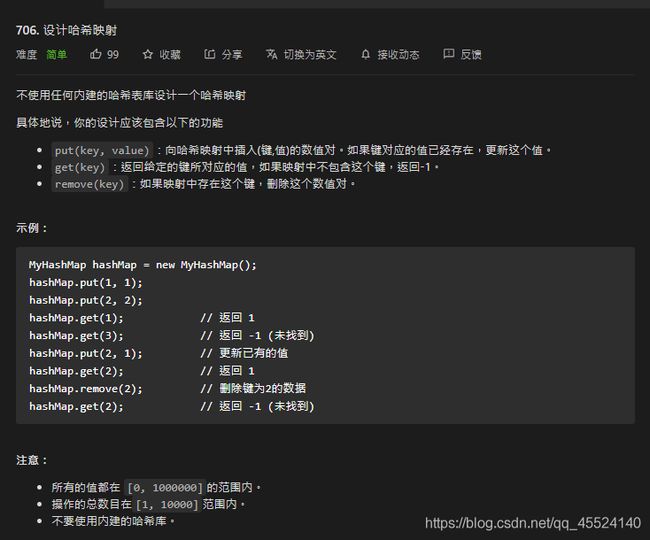
1.LeetCode 706.设计哈希映射

代码如下：

#define TSize 1001

typedef struct{
    int key;
    int value;
    struct HashNode *next;
} HashNode;

typedef struct {
    HashNode* HashTable;
    int TableSize;
} MyHashMap;


MyHashMap* myHashMapCreate() {
    MyHashMap* obj = (MyHashMap*)malloc(sizeof(MyHashMap));
    obj->HashTable = (HashNode*)calloc(TSize, sizeof(HashNode));
    obj->TableSize = TSize;
    for(int i = 0; i < obj->TableSize; i++){
        obj->HashTable[i].next = NULL;
        }
    return obj;
}

void myHashMapPut(MyHashMap* obj, int key, int value) {
    int pos = key % obj->TableSize;
    HashNode* cur = (&obj->HashTable[pos])->next;   //或者obj->HashTable[pos].next
    while(cur != NULL){
        if(cur->key == key){
            cur->value = value;
            return;
            }
        cur = cur->next;
        }
    //未找到相同的key，添加节点，头插法
    HashNode* node = (HashNode*)malloc(sizeof(HashNode));
    node->key = key;
    node->value = value;
    node->next = (&obj->HashTable[pos])->next;
    (&obj->HashTable[pos])->next = node;
}

int myHashMapGet(MyHashMap* obj, int key) {
    int pos = key % obj->TableSize;
    HashNode* cur = (&obj->HashTable[pos])->next;
    while(cur != NULL){
        if(cur->key == key){
            return cur->value;
            }
        cur = cur->next;
        }
    return -1;
}

void myHashMapRemove(MyHashMap* obj, int key) {
    int pos = key % obj->TableSize;
    HashNode* cur = (&obj->HashTable[pos])->next;
    while(cur != NULL){
        if(cur->key == key){
            cur->key = -1;  //懒惰删除
            return;
            }
        cur = cur->next;
        }
}

void myHashMapFree(MyHashMap* obj) {
    free(obj->HashTable);
    free(obj);
}

2.LeetCode 49.字母异位词分组

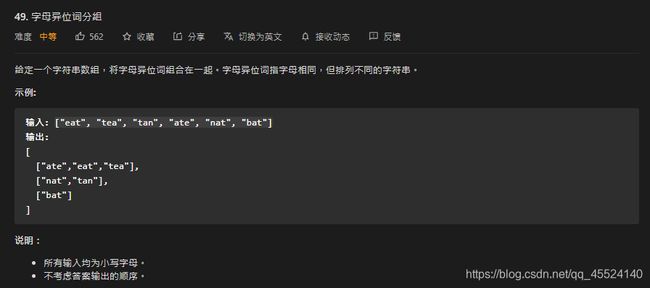
这题考察了键为字符串的情况，我们使用一个简单的散列函数，即将每个字符的ASCII码的和模上表长即可。
代码如下：

void StrSort(char* str, int slen){  //由于全是小写字母，就可以使用桶排序了
    int buf[26] = {0};
    for(int i = 0; i < slen; i++){
        buf[str[i] - 'a']++;
        }
    int size = 0;
    for(int i = 0; i < 26; i++){
        while(buf[i] > 0){
            str[size++] = i + 'a';
            buf[i]--;
            }
        }
    str[size] = '\0';
}

int size;

//字符串哈希（将排序后的字符串作为键）
typedef struct{
    char* key;
    int value;  //表示是第几行
    struct HashNode* next;
} HashNode;

typedef struct{
    HashNode* hashTable;
    int TableSize;
} HashMap;


HashMap* BuildHashMap(int TSize){
    HashMap* obj = (HashMap*)malloc(sizeof(HashMap));
    obj->hashTable = (HashNode*)calloc(TSize, sizeof(HashNode));
    for(int i = 0; i < TSize; i++){
        obj->hashTable[i].next = NULL;
        }
    obj->TableSize = TSize;
    return obj;
}

int Insert(HashMap* obj, char* str, int slen){    //返回此字符串应该加入的位置
    int Hashval = 0;
    char* tmp = (char*)calloc(slen + 1, sizeof(char));
    strcpy(tmp, str);
    StrSort(tmp, slen);    //如果是字母异位分词，排序后应该相同，哈希函数的值相同
    for(int i = 0; i < slen; i++){  //Hash(x) = str[0] + ... + str[slen - 1];
        Hashval = Hashval + str[i];
        }
    int pos = Hashval % obj->TableSize;
    HashNode* cur = (&obj->hashTable[pos])->next;
    while(cur != NULL){
        if(strcmp(tmp, cur->key) == 0){
            free(tmp);
            return cur->value;
            }
        cur = cur->next;
        }
    
    HashNode* node = (HashNode*)malloc(sizeof(HashNode));
    node->key = (char*)calloc(slen + 1, sizeof(char));
    strcpy(node->key, tmp);
    node->value = size++;
    node->next = (&obj->hashTable[pos])->next;
    (&obj->hashTable[pos])->next = node;
    free(tmp);
    return node->value;
}


char *** groupAnagrams(char ** strs, int strsSize, int* returnSize, int** returnColumnSizes){
    *returnSize = 0;
    size = 0;
    *returnColumnSizes = (int*)calloc(strsSize, sizeof(int));
    HashMap* obj = BuildHashMap(strsSize);
    char*** res = (char***)calloc(strsSize, sizeof(char**));
    for(int i = 0; i < strsSize; i++){
        res[i] = (char**)calloc(5, sizeof(char*)); //这里如果空间分配多了直接爆内存，但是按理说应该考虑所以字符串共一行和一个字符串一行的情况
        }
    for(int i = 0; i < strsSize; i++){
        int slen = strlen(strs[i]);
        int pos = Insert(obj, strs[i], slen);
        res[pos][(*returnColumnSizes)[pos]] = (char*)calloc(slen + 1, sizeof(char));
        strcpy(res[pos][(*returnColumnSizes)[pos]++], strs[i]);
        }
    *returnSize = size;
    free(obj->hashTable);
    free(obj);
    return res;
}

开放定址法

​ 分离链接法的缺点是需要指针，依次分配新的内存空间需要消耗一定的时间，而开放定址法使用了数组来进行存储，如果产生冲突，就尝试另外的单元，直到找出空的单元为止。常用的方法有两种：线性探测法和平方探测法，开放定址法的实际插入为可以表示为以下公式：
$$h(x)=(Hash(x)+F(i))\%TableSize$$
F(i)表示增量函数

线性探测法

​ 在遇到冲突时，向下一个单元探测，如果单元为空就插入相应元素，增量函数可以表示为：
$$F(i)=i，i=0,1,2...,n$$
使用线性探测法在表长足够的情况下可以保证每个元素都能插入表中，但是缺点会导致一次聚集，即前面插入的元素占了后面插入元素的位置，导致新插入的元素都聚集在一块，这样会影响算法的效率，因此，出现了以下的方法。

平方探测法

​ 平方探测法是消除线性探测中一次聚集问题的冲突解决方法，增量函数可以表示为：$F(i)=\pm i^2$

,但是为了方便起见，我们一般选择只带正增量的平方探测，即：
$$F(i)=i^2，i=0,1,2...,n$$
虽然平方探测可以优化插入效率，但是如果表长不符合要求，会出现一个元素无法插入表中的情况，即一直无法探测到空的单元格，对此，根据证明，如果使用平方探测，且表的大小是素数，那么当表至少有一半是空的时候，总能够插入一个新的元素。所以，我们只要保证表长是大于插入元素个数的两倍的素数即可保证新元素的插入可行。

bool isPrime(int x){
    if(x < 2) return false;
    int n = sqrt(x);
    for(int i = 2; i <= n; i++){
        if(x % i == 0){
            return false;
        	}
    	}
    return true;
}

//得到适合的表长
int PrimeSize(int Size){
    int TSize = Size * 2 + 1;
    while(!isPrime(TSize)){
        TSize++;
    	}
    return TSize;
}

总结：使用拉链法不用担心元素无法插入的问题，使用开放定址法在时间效率上略快于分离链接法，并且代码相对来说更容易实现，但是如果要删除元素，标准的删除操作不能施行，因为删除的单元可能引起过冲突，因此需要懒惰删除，即用一个特殊的数（不会被插入的元素）代替单位内容，且这个单元之后不能再被使用了。

相关例题：

这里提供两道习题作为参考，分别考虑了能全部插入和不能全部插入的情况。

1.LeetCode 705.设计哈希集合

代码如下：

//为了防止有元素无法插入，保证表长为大于20000的素数
#define TSize 20001   

typedef struct {
    int* HashTable;
    int TableSize;
} MyHashSet;

//HashTable[i] = -1表示i位置为空，-2表示此位置被删除
MyHashSet* myHashSetCreate(){
    MyHashSet* obj = (MyHashSet*)malloc(sizeof(MyHashSet));
    obj->HashTable = (int*)calloc(TSize, sizeof(int));
    memset(obj->HashTable, -1, sizeof(int) * TSize);
    obj->TableSize = TSize;
    return obj;
}

void myHashSetAdd(MyHashSet* obj, int key){
    int pos = key % obj->TableSize;
    for(int i = 0; ; i++){
        int nextpos = (key + i * i) % obj->TableSize;
        if(obj->HashTable[nextpos] == -1){
            obj->HashTable[nextpos] = key;
            break;
            }
        else if(obj->HashTable[nextpos] == key){    //如果已经有了就不插入了
            break;
            }
        }
}

void myHashSetRemove(MyHashSet* obj, int key){
    int pos = key % obj->TableSize;
    for(int i = 0; ; i++){
        int nextpos = (key + i * i) % obj->TableSize;
        if(obj->HashTable[nextpos] == key){
            obj->HashTable[nextpos] = -2;   //懒惰删除，用-2标示
            break;
            }
        else if(obj->HashTable[nextpos] == -1){ //未找到元素
            break;
            }
        }
}


bool myHashSetContains(MyHashSet* obj, int key) {
    int pos = key % obj->TableSize;
    for(int i = 0; ; i++){
        int nextpos = (key + i * i) % obj->TableSize;
        if(obj->HashTable[nextpos] == key){
            return true;
            }
        else if(obj->HashTable[nextpos] == -1){ //未找到元素
            return false;
            }
        }
}

void myHashSetFree(MyHashSet* obj) {
    free(obj->HashTable);
    free(obj);
}

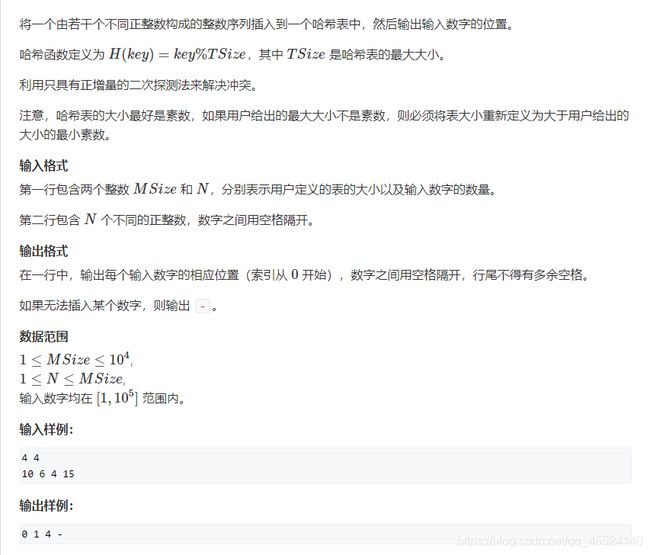
2.AcWing 1564.哈希

代码如下：

#include 
#include 
#include 

bool isPrime(int x){
    if(x < 2) return false;
    int n = sqrt(x);
    for(int i = 2; i <= n; i++)
        if(x % i == 0) return false;
    return true;
}

int getSize(int Size){
    int x = Size;
    while(!isPrime(x)) x++;
    return x;
}

int main(void){
    int MSize, N;
    scanf("%d %d", &MSize, &N);
    int TSize = getSize(MSize);
    int* HashTable = (int*)calloc(TSize, sizeof(int)); 
    int Key;
    while(N--){
        scanf("%d", &Key);
        int pos = Key % TSize;
        bool check = false;
        for(int i = 0; ; i++){
            int nextpos = pos + i * i;
            if(nextpos < TSize){
                if(HashTable[nextpos] == 0){
                    HashTable[nextpos] = Key;
                    check = true;
                    printf("%d", nextpos);
                    break;
                    }
                }
            else{
                nextpos %= TSize;
                if(nextpos == pos) break;
                if(HashTable[nextpos] == 0){
                    HashTable[nextpos] = Key;
                    check = true;
                    printf("%d", nextpos);
                    break;
                    }
                }
            }
        if(check == false) printf("-");
        if(N != 0) printf(" ");
        }
    free(HashTable);
    return 0;
}