随机过程（上）：马尔可夫链

随机过程是数学专业非常经典的一门课，在很多领域都有应用，之前谈论过的时间序列分析也和这门课息息相关，没想到这学期又遇上了，趁着期末复习简单总结一下，只是整理一下概念，所以就不深入进行推导了。因为教材是英文的，所以部分术语会用英文，免得翻译不准确，当然一些大家都知道的术语还是用中文，毕竟打字比较方便。

虽然学数学就应该用数学的语言去理解和表达，但是这样写文章一方面打字确实很费时间，另一方面我也只是想整理一下概念和概念之间的联系，所以很多地方都说得比较通俗，最终我们还是应该以标准的文献资料为准。

还有一点想说的是，随机过程理论完善的过程是一个非常有趣的过程，从最开始一个简单的定义、理想的情况开始，不断抽象、联想，不断进行推演，最终发展成完整的一个理论，从中就可以感受到数学的那种充满逻辑的魅力。

首先，我们想一下天气预报这个问题，我们应该怎么对天气的变化进行分析预测？数学家就提出，把天气看成一个随机变量X，和时间t一起构建一个随机变量族，这个随机变量族{X,T}就称为一个随机过程。这是一个简单的定义，也是一切的起源。

定义是为了更方便、规范地进行描述，可是要分析复杂的天气变化依然很难，所以数学家就想着从最简单的情况开始，假设今天的天气只和前一天有关，这个假设就称为马尔科夫性，更规范地说，就是对一个随机变量族{X,T}，假设tn的状态x只和tn-1的状态有关，和tn-2等历史数据都没有关系。

$$Pr(X-t\in A|X_{S_1}=x_{S_1},...,X_{S_n}=x_{S_n},X_s=x)=Pr(X_t\in A|X_S=x)$$

用通俗的话来说，就是今天下不下雨只和昨天下不下雨有关，和前天大前天的天气都没有关系。

在这里，天气的状况、时间（天数）都是离散的，所以我们就称这样的一个具有马尔科夫性、具有离散时间离散状态的随机过程为马尔科夫链，除了离散时间离散状态当然还会有连续的时间和连续的状态，不过我们还是需要循序渐进，先从最简单的马尔科夫链开始说起。

马尔可夫链因为时间状态都是离散的，所以最好分析。为了描述一个马尔可夫链，我们引出几个新概念，第一个是状态转移概率，比如说今天下雨明天晴天的概率为0.1，这就是一个状态转移概率。由状态转移概率可以构成一个转移矩阵，转移矩阵描述了所有状态之间的转移概率，比如矩阵的一行二列就表示状态一转移到状态二的概率，当然这个概率是单步演变的概率。

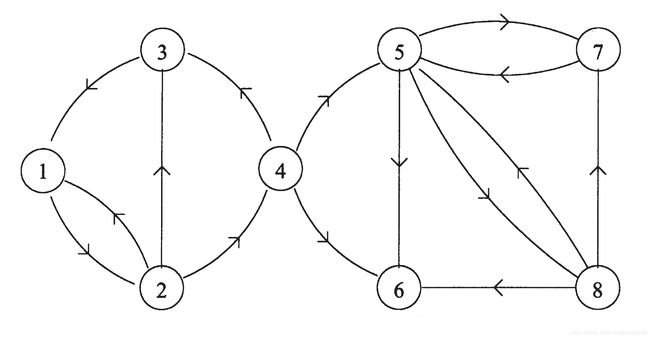
除此之外，还有转移图，它是根据转移矩阵画出来的有向图结构，毕竟不是每个状态之间都能相互转移的，所以我们就能通过有向图直观地表示状态与状态之间的转移情况。

有了初始概率分布和转移矩阵是不是就能描述出整个马尔科夫链呢，也不一定，因为转移矩阵可能会随着时间改变，所以我们这里也可以进一步假设转移矩阵是不变的，同时定义这样的马尔科夫链为Time-homogeneous Markov chains。

$$P_{ij}(n,n+1)=p_{ij}$$

$$where{P}_{ij}(n,n+1)=Pr(X_{n+1}=j|x_n=i)$$

所以到目前为止，我们就得到了最最简单的随机过程：具有马尔科夫性、时间状态都是离散的、转移矩阵不随时间改变的随机过程。

对于Time-homogeneous Markov chain我们可以分析总结它的一些性质，从而根据这些性质对它进行进一步的分类。

第一个性质是不可约性Irreducibility，如果马尔可夫链的状态空间只有一个连通类，也就是说状态之间可以随意转换，这个马尔可夫链就具有不可约性。比如说穷和富这两个状态，相互可以自由转换，这样构成的一个转移矩阵就是不可约的，而健康和死亡这两个状态则不一样，一旦从健康转换到死亡，就无法回到健康状态，所以死亡这个状态也成为吸收态。

第二个是重现性（recurrence），如果马尔可夫链到达一个状态后还能反复回到这个状态，则该状态具有重现性，如果永远都回不去，就说它具有瞬变性（transience）。

第三个是周期性（periodicity），如果马尔可夫链可以按一定周期，不断重现一个状态，那么这个状态就具有周期性。举个例子，从状态i出发，只在n为偶数的情况下才有可能返回状态i，就称这个状态具有周期为2的周期性。

第四个是遍历性（ergodicity），简单来说就是任意取一个时间段，所有状态都有出现的可能。

根据这些性质我们可以对马尔科夫链进行进一步的分析，分析的内容有很多，这里主要针对stationary distribution说一下。

首先什么是stationary distribution，

$$\pi =\pi P$$

pi是状态的概率分布，也就是说状态经过一次变化，状态的概率分布也不会变化，举个最简单的例子，现在有一个转移矩阵，富人变穷人、穷人变富人、富人保持原状、穷人保持原状的概率都是0.5，穷人富人的概率分布也都是0.5，那么算一下就知道经过一次转移，下一时刻穷人富人的概率分布各自都还是0.5，这时候这个状态概率分布就是stationary的。

一般来说，我们如果要求出stationary distribution，其实就是求解方程解出pi，至于有没有解其实是和转移矩阵P相关联的，再联想到前面的不可约性、重现性之类的性质，其实就是用来对P进行分析从而帮助判断pi的存在性唯一性之类的问题的。比如说一个具有有限状态的马尔科夫链，如果他具有不可约性，那么他就有唯一的stationary distribution。诸如此类的定理可以查阅文献详细看看，这里就暂时不说了。

除了stationary distribution，我们还会对马尔科夫链的long-term behaviour比较感兴趣，比如说当n趋于无穷的时候，状态概率分布会不会趋于稳定，比如说像人，随着年纪增大死的概率也会变大，到了一两百岁死的概率基本上可以等于1，这就是一个极限分布。除了概率分布，如果转移矩阵随着时间改变的话，也可以研究转移矩阵是否存在一个极限，所以其实会有很多问题值得研究的。