六种字符串匹配算法详解（含代码演示）
1. Brute-Force算法
2. Rabin-Karp Hash算法
3. Kmp算法
4. Kmp的优化算法
5. Sunday算法
6. Shift-And算法
ps：字符串匹配其实是单模匹配问题
1.Brute-Force 朴素匹配算法（暴力匹配）
时间复杂度：O(n*m)
//返回 文本串s中第一次查找到模式串t的位置
int brute_force(const char *s, const char *t){
//扫描文本串的每一位
for(int i = 0; s[i]; i++){
bool flag = true;
//用当前的第i位和模式串向后比较
for(int j = 0; t[j]; j++){
if(s[i + j] == t[j]) continue;
flag = false;
break;
}
if(flag) return i;
}
return -1;
}
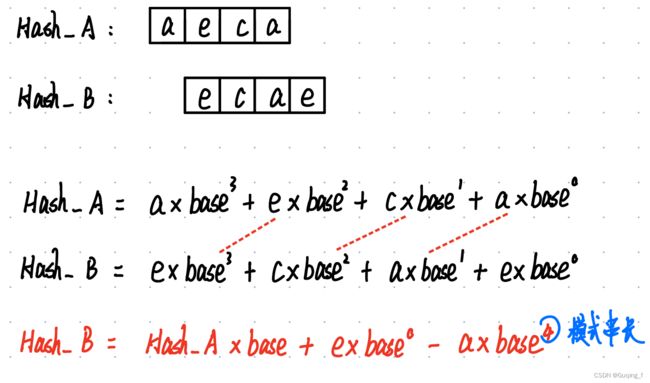
2.Rabin-Karp Hash匹配法
时间复杂度：O(n * m / P)
P最好取质数，则最大可以出现P-1种余数，冲突概率为1 / P。当P ~= m，时间复杂度 ~= O(n)
Hash值计算：
#includeq1:两个不同的字符串拥有相同的哈希值怎么办？
**ans1：**正常比较即可
q2：算法的时间复杂度？
ans2： O(n * m / P)。合理选择P是hash匹配算法的关键
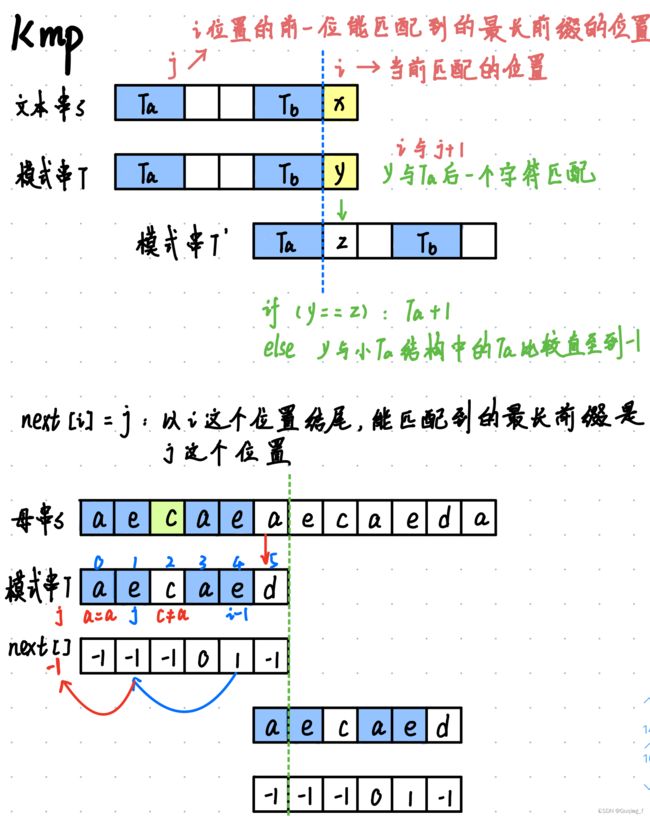
3.KMP算法
时间复杂度O(n + m)
NFA：不确定性有穷状态自动机
int *getNext(const char *t, int *len){
*len = strlen(t);
int *next = (int *) malloc (sizeof(int) * (*len)); // next[i] = j : 以i位置结尾，所匹配到的最长前缀是j这个 位置
next[0] = -1; //匹配最长前缀不能包含自己，第一位的最长前缀为-1
for(int i = 1, j = -1; t[i]; i++){
//i是当前匹配的位置，j是i的前一位能匹配到的最长前缀的位置。所以i与j+1比较
while(j != -1 && t[j + 1] != t[i]) j = next[j]; //匹配不成功就往前找
if(t[j + 1] == t[i]) ++j; //匹配成功就按照i-1位置最长前缀的数量+1
next[i] = j;//更新next数组
}
return next;
}
int kmp(const char *s, const char *t){
int len = 0;
int *next = getNext(t, &len); //初始化next数组
//j代表之前成功匹配过的模式串在第几位
for(int i = 0, j = -1; s[i]; i++){
while(j != -1 && t[j + 1] != s[i]) j = next[j]; //NFA(不确定性)
if(t[j + 1] == s[i]) ++j;
if(t[j + 1] == '\0') { //完全成功匹配了模式串
free(next);
return i - len + 1;
}
}
free(next);
return -1;
}
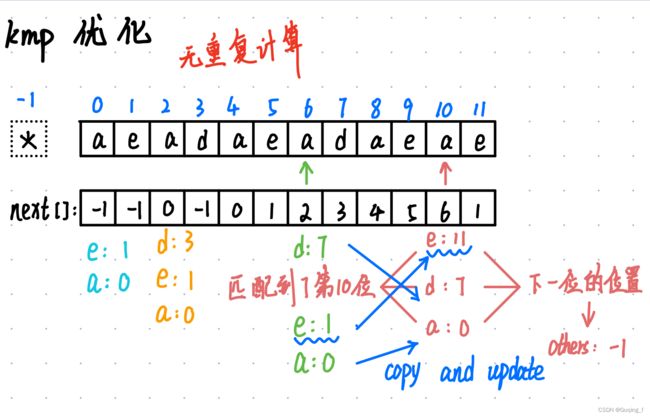
4.KMP的优化：
DFA：确定性有穷状态自动机
void free_next(int *next){
free(next);
return ;
}
void free_jump(int **jump, int len){
for(int i = 0; i < len; i++) free(jump[i - 1]);
free(jump - 1);
return ;
}
//获取跳转信息的数组
int **getJump(int *next, const char *t, int n){
int **jump = (int **) malloc(sizeof(int *) * n);
for(int i = 0; i < n; i++) jump[i] = (int *) malloc(sizeof(int) * 26);
++jump; //让jump指向next数组1的位置，使它访问-1位置的时候实际上访问的是0，合法的
for(int i = 0; i < 26; i++) jump[-1][i] = -1;
jump[-1][t[0] - 'a'] = 0; //模式串的第一个字符
for(int i = 0, I = n - 1; i < I; i++){
for(int j = 0; j < 26; j++) jump[i][j] = jump[next[i]][j];
jump[i][t[i + 1] - 'a'] = i + 1;
}
return jump;
}
//Kmp的优化算法
int kmp_opt(const char *s, const char *t){
int len = 0;
int *next = getNext(t, &len);
int **jump = getJump(next, t, len);
//j代表之前成功匹配过的模式串在第几位
for(int i = 0, j = -1; s[i]; i++){
j = jump[j][s[i] - 'a']; //DFA(确定性)
if(j == len - 1){ //已找到字符串
free_next(next);
free_jump(jump, len);
return i - len + 1;
}
}
free_next(next);
free_jump(jump, len);
return -1;
}
4.Sunday算法
匹配效率比KMP高，只需统计每个字母最后一次出现的位置
int brute_one_match(const char *s, const char *t){
printf("brute_one_match_called\n");
for(int j = 0; t[j]; j++){
if(s[j] == t[j]) continue;
return 0;
}
return 1;
}
int sunday(const char *s, const char *t){
int tlen = strlen(t), slen = strlen(s);
//计算每一种字符出现在字符串的倒数第几位
int jump[128] = {0};
//默认每个字符出现在模式串的-1位
for(int i = 0; i < 128; i++) jump[i] = tlen + 1;
//扫描模式串的每一位。t[i]字母出现在倒数第tlen-i位
for(int i = 0; t[i]; i++) jump[t[i]] = tlen - i;
for(int i = 0; i + tlen <= slen; ){
//按位比较，判断当前匹配能否成功
if(brute_one_match(s + i, t)) return i;
//暴力匹配不成功，计算黄金对齐点位
i += jump[s[i + tlen]];
}
return -1;
}
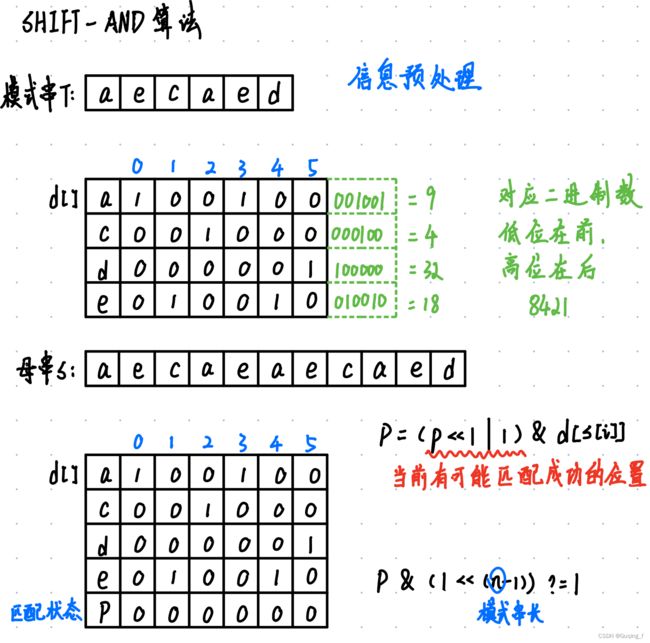
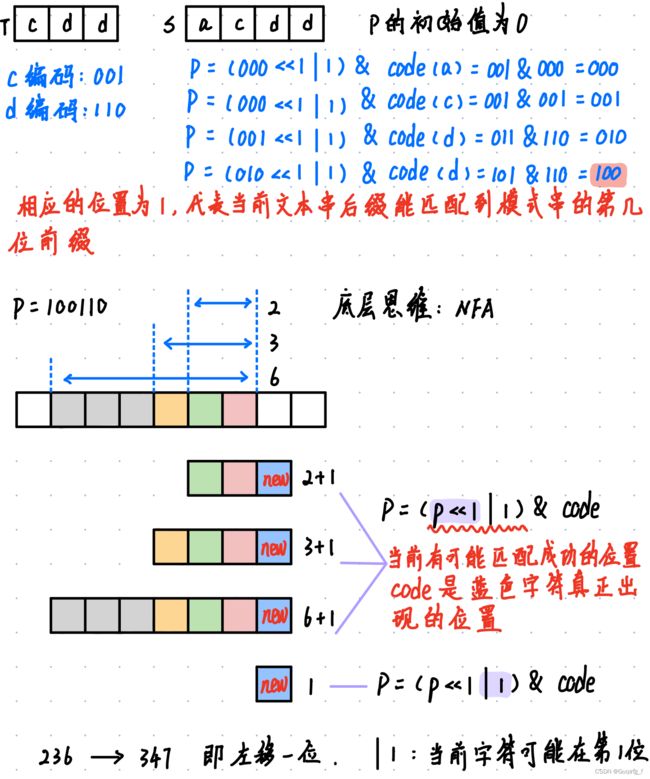
5.Shift-and算法
效率也比Kmp高
底层思维也是NFA
int shift_end(const char *s, const char *t){
int code[128] = {0}, n = 0;
// |= :按位或赋值。x |= 2：计算按位或值2和变量x中的值，并使用按位或赋值运算符将结果分配回x
//扫描模式串的每一位。将t[n]字符的第n位置为1
for( ; t[n]; n++) code[t[n]] |= (1 << n);
int p = 0;
for(int i = 0; s[i]; i++){
p = (p << 1 | 1) & code[s[i]];
if(p & (1 << (n - 1))) return i - n + 1;//p的第n位为1，匹配成功，返回匹配成功的起始位置
}
return -1;
}
要是对您有帮助，点个赞再走吧~ 欢迎评论区讨论~