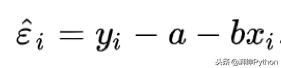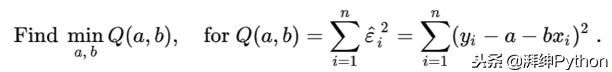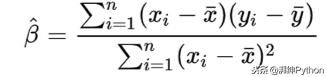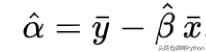机器学习：线性回归

https://www.toutiao.com/a6639148240874766852/

 

2018-12-26 12:05:58

使用Python从头开始的线性回归

可以说，任何Python项目的第一部分都是导入一堆有用的包。这里最重要的包是：

·NumPy - 用于科学计算的软件包

·Pandas - 一个为数据存储和检索提供便捷方法的软件包

·matplotlib＆seaborn - 绘图库

%matplotlib inline
import scipy.stats as stats
import numpy as np
import pandas as pd
import math
import seaborn as sns
import matplotlib.pyplot as plt
plt.style.use('ggplot')

接下来，为了构建线性回归，我们需要一些数据。因此，我们将生成一些虚拟数据：

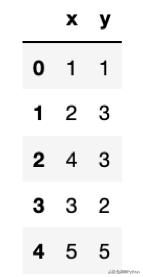
data = pd.DataFrame({'x': [1, 2, 4, 3, 5], 'y': [1, 3, 3, 2, 5]})

我们现在可以看看这些数据：

 

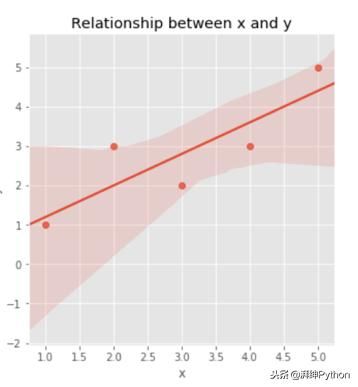
此数据框提供了所有必要的信息，但通常最好的是绘制我们的数据图以更直观地理解变量x和y之间的关系：

 

x和y之间似乎存在线性关系。来自seaborn的这个lmplot甚至适合回归线。

线性回归构件块

在数学生涯的某些阶段，您很可能会遇到以下公式：

 

具有截距α和斜率β的线。

我们引入残差。残差描述了使用上述函数对数据点的估计值是多少。

 

为了使我们的回归尽可能接近我们的数据，我们自然希望在所有数据点上最小化这些残差。这可以使用以下公式表示：

 

所有这些都表明我们希望最小化我们预测的平方误差之和。通过扩展此公式，我们可以找到我们对alpha和beta的最佳估计。让我们从beta开始，最后进入一些Python代码：

 

首先让我们计算公式的x和y的平均值：

mean_x = np.mean(data.x)
mean_y = np.mean(data.y)
print('The mean of x is {} and the mean of y is {}'.format(mean_x, mean_y))
#The mean of x is 3.0 and the mean of y is 2.8

借助我们的手段，我们可以开始构建分子

 

在下面的代码片段中，numerator1指的是分子的左边部分，numerator2指的是右边的部分。

numerator1 = data.x - mean_x
numerator2 = data.y - mean_y
print('x values: 
', numerator1, '

', 'y values: 
', numerator2)
#x values: 
# 0 -2.0
#1 -1.0
#2 1.0
#3 0.0
#4 2.0
#Name: x, dtype: float64 
#
# y values: 
#0 -1.8
#1 0.2
#2 0.2
#3 -0.8
#4 2.2
Name: y, dtype: float64
numerator = np.sum(numerator1 * numerator2)
numerator
#8.0

我们完成了分子！现在剩下的就是计算分母。

 

但是，我们甚至不需要重新开始。分母只是分子numerator1的平方！

denominator = np.sum(numerator1 **2)
denominator
#10.0

我们到了那里。现在，要获得我们的beta估计，我们所要做的就是将分子和分母组合在一起：

beta1 = numerator/denominator
print('beta1 is: {}'.format(beta1))
#beta1 is: 0.8

请注意，虽然公式将截距称为alpha，但我将其称为beta零。

完成测试后，我们可以将结果与手段一起插入以下公式中以获得拦截：

 

在Python中：

beta0 = mean_y - beta1 * mean_x
print('beta0 is: {}'.format(beta0))
#beta0 is: 0.39999999999999947

我们现在有了回归线的等式：y = 0.4 + 0.8x。Beta和alpha也称为“最小平方系数”，因为我们只是将平方误差最小化并达到beta和alpha。因此，这种推导它们的方法被称为“普通最小二乘法”或简称OLS。我们将使用这个等式来预测我们的数据。

做出预测

现在到了有趣的部分：使用我们的回归方程来根据x值预测数据的y值。所要做的就是用数据中x的一列代替我们的衍生回归方程中的x：

predicted_y = beta0 + beta1 * data.x
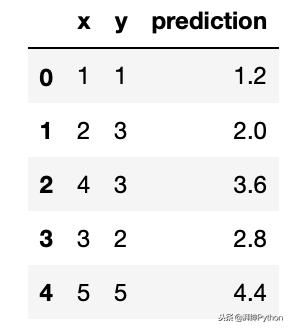
after_pred = pd.concat([data.x, data.y, predicted_y.rename('prediction')], axis=1)
after_pred

原始X和Y值与我们的预测相对应

让我们绘制我们的预测，看看他们如何与本文开头中的回归线进行比较。

plt.figure(figsize=(8,6))
original_y = plt.scatter(data.x, data.y, marker ='^', s=70)
predicted_y = plt.scatter(data.x, after_pred.prediction, s=70)
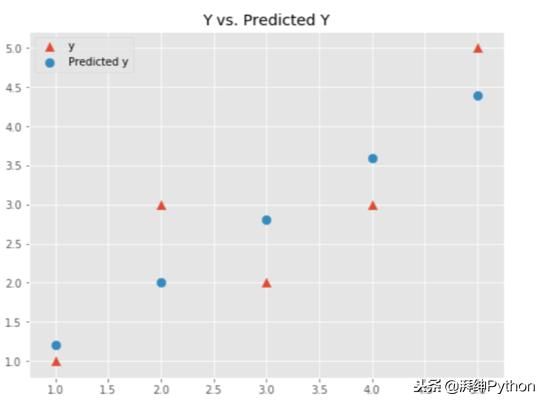
plt.title('Y vs. Predicted Y')
plt.legend((original_y, predicted_y), ('y', 'Predicted y')) 

 

蓝点，我们的预测，形成一条直线，非常类似于我们之前在图中看到的线！我们的回归似乎有效！在调用它之前我们应该先看一下的是回归模型的表现。

估计错误

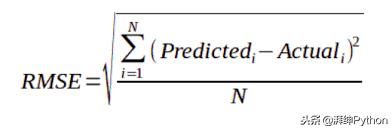
虽然有几种方法可以测量误差并因此模拟性能，但为了简单起见，我将坚持使用RMSE（均方根误差）。

 

Python实现：

rmse = math.sqrt(np.mean((after_pred.prediction-data.y)**2))
print('Our RMSE is {}'.format(rmse))
#Our RMSE is 0.692820323027551

这意味着，我们的每个预测都偏差约0.69。