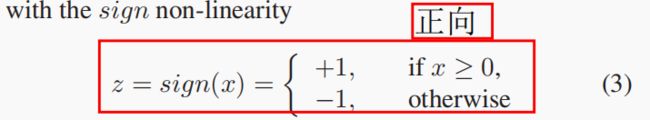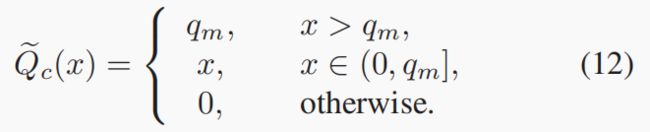HWGQ-Deep Learning with Low Precision by Half-wave Gaussian Quantization论文学习

论文链接：https://openaccess.thecvf.com/content_cvpr_2017/html/Cai_Deep_Learning_With_CVPR_2017_paper.html

摘要

研究了深度神经网络激活的量化问题一直是研究热点。对流行的二值量子化方法的检验表明，它由一个经典的非线性，双曲切线：一个分段常数函数，用于前馈网络计算，以及一个分段线性硬阈值函数，用于网络学习过程中的反向传播步骤。然后考虑了广泛使用的ReLU非线性的逼近问题。提出了一种half-wave Gaussian quantizer半波高斯量化归一化器(HWGQ)，利用网络激活和批归一化操作的统计量，证明了它具有良好的实现能力。为了克服梯度失配的问题，由于使用了不同的前向逼近和后向逼近，然后研究了几个分段向后逼近器。所得到的量化网络的实现，表示为HWGQ-Net，比以前可用的低精度网络，具有1位二进制权值和2位量化激活，更接近于AlexNet，ResNet、谷歌和VGG-Net等全精度的网络。

1. 引言

困难在于，激活的二值化或量化需要使用不可微操作符进行处理，这给反向传播算法造成了问题。这将在计算网络输出的前馈步骤和计算学习所需的梯度的反向传播步骤之间进行迭代。困难在于二值化或量化算子具有逐步的响应，在反向传播过程中产生非常微弱的梯度信号，降低了学习效率。到目前为止，这个问题已经通过使用前馈步骤中使用的算子的连续近似来实现反向传播步骤来解决。然而，这就在实现了前向计算的模型和用于学习它的导数之间造成了一种不匹配，从而导致了一个次优模型。
在本工作中，我们将前馈步骤中使用的量化算子和反向传播步骤中使用的连续近似看作是近似每个网络单元的激活函数的两个函数。我们把这些称为激活函数的前向和向后近似。我们首先考虑在[4,30]中使用的二进制±1量化器，为此这两个函数可以看作是一个非线性激活函数的离散和连续近似，即双曲切线，在经典神经网络中经常使用。然而，这种激活在最近的深度学习文献中并不常用，其中ReLU非线性获得了更大的优势。这正是因为它产生了更强的梯度幅度。当双曲切线或s型非线性是压缩非线性的，且大部分是平坦的时，ReLU是一个半波整流器，对正输入有线性响应。因此，当双曲切线的导数几乎在各处都接近于零时，ReLU沿着整个轴的正范围都有单位导数。
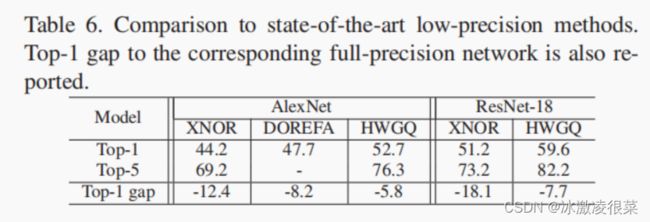
为了提高量化网络的学习效率，我们考虑了ReLU的前后向逼近函数的设计。为了离散其线性分量，我们建议使用一个最优量化器。通过利用文献中常用的网络激活和批处理归一化操作的统计数据，我们表明这可以用一个半波高斯量化器(HWGQ)来完成，它不需要学习，而且计算效率非常高。虽然最近的一些作品尝试了类似的思想[4,30]，但他们设计的量化器并不足以保证良好的深度学习性能。我们通过对适当的后向近似函数的研究来解决这个问题，该函数解释了正向模型和反向传播的导数之间的不匹配。本研究建议采用线性化、梯度剪切或梯度抑制等操作来实现后向逼近。我们表明，向前HWGQ与这些向后操作产生非常高效的低精度网络，称为HWGQ-net，性能更接近连续模型，如AlexNet[21]，ResNet[12]谷歌[34]和VGG-Net[33]，比其他低精度网络的文献。据我们所知，这是第一次有一个单一的低精度算法能够在如此多的流行网络上取得成功。使用[30]的参数，HWGQ-Net（1位权重和2位激活）理论上可以实现∼32×内存和∼32×卷积计算节省。这表明，HWGQNet对于在现实世界的应用中部署最先进的神经网络是非常有用的。

2. 相关的工作

由于激活的量化可以进一步加速和减少训练记忆的需求，它引起了一些[35,24,4,30,37,23,26]的注意。[35,24]在网络训练后进行量化，避免了不可微优化的问题。最近，[4,30,37]试图通过在反向传播步骤中使用量化器函数的连续逼近来解决不可微优化问题。[23]对梯度失配问题提出了几种可能的解决方案，[26,37]表明，在反向传播步骤中，梯度可以用少量的比特进行量化。虽然其中一些方法在CIFAR-10上取得了良好的结果，但没有一种方法能在大规模分类任务上能够与全精度模型竞争，如ImageNet[32]。

3. 二值网络

3.2 权重二值化

基于XNOR-Net的方法。

3.3 激活二值化

正向：

反向：

这些近似有两个主要问题。第一个问题是它们近似于双曲切线(tanh)，这是一个压扁的非线性。压缩非线性(如值或s形)的饱和行为强调了导数消失的问题，影响了反向传播的有效性。第二个问题是，在正向公式（3）以及反向（5）之间产生了前向网络以及导数需要学习的差异。因此，反向传播可能是高度次优的。这被称为“梯度不匹配”问题。

4. Half-wave Gaussian Quantization

在本节中，我们提出了另一种量化策略，即ReLU非线性的近似。

4.1. ReLU

g(x) = max(0,x) (6)
ReLU是半波整流器现在众所周知，与压缩非线性相比，它在（1）中的使用显著提高了反向传播算法的识别效率。我们提出使用一个量化器Q(x)在前馈中近似（6）和一个合适的分段线性逼近其导数用于反向传播步骤。

4.2 前向近似

量化器是一个分段常数函数，
![在这里插入图片描述](https://img-blog.csdnimg.cn/fcd1309108fd4bbea41dd0604926e30d.png

4.3 反向近似

4.3.1 Vanilla ReLU

由于（6）的ReLU已经是一个分段的线性函数，因此似乎可以使用ReLU本身，即普通的ReLU，作为向后近似函数。这对应于使用导数

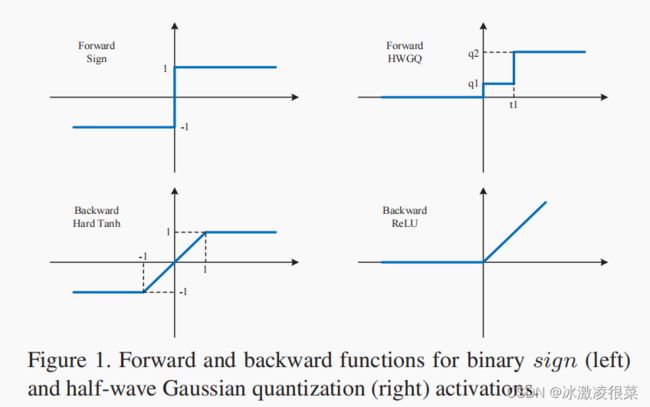
注意，虽然后向近似是精确的，但它并不等于前向近似。因此，存在一个梯度不匹配。比如x>0，近似值Q（x）由ReLU有错误∣Q（x）− x∣.这是上限的(ti+1 −qi)对于x∈ (ti,ti+1],但是当x∈ (ti+1,∞)量化误差没有上限.因此，对于大值，不匹配特别大。由于这些是x分布尾部的值，因此说ReLU与Q（X）有很大的不匹配“在尾巴上。”当使用ReLU在（4）中来近似时梯度时，它可以产生非常不准确的梯度。根据我们的经验，这可能会使学习算法不稳定。
这是鲁棒估计文献中的一个经典问题，其中异常值会过度地影响学习算法[14]的性能。对于量化，在x超过qmax的概率很小，大的点积是有效的异常值。缓解离群值的经典策略是限制误差函数的增长率，在这种情况下是.因此，问题是ReLU的单调性超出了这个范围x= qmax.为了解决这个问题，我们研究了较慢增长率的替代向后近似函数。

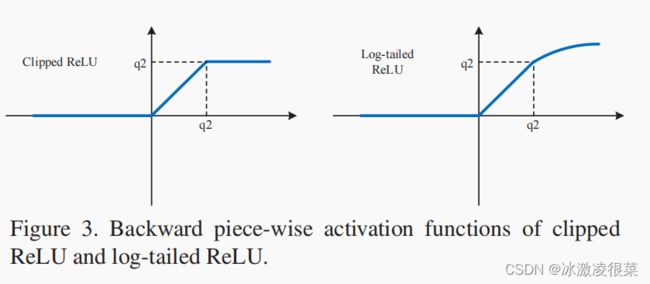
4.3.2 截断relu

4.3.3 Log-tailed ReLU

当在（4）中使用导数时对数尾ReLU与初始ReLU相同，但给大于这个的振幅的权重减小。它的行为就像原始ReLU（单位衍生物）当0

5. 实验结果