《视觉 SLAM 十四讲》V2 第 8 讲 视觉里程计2 【如何根据图像 估计 相机运动】【光流 —＞ 直接法】

OpenCV关于 光流的教程

第 8 讲 视觉里程计 2

P205 第8讲
光流法 跟踪 特征点
直接法 估计相机位姿
多层直接法

8.1 直接法

第 7 讲 使用特征点 估计 相机运动
缺点：
1、关键点的提取 与 描述子的计算 非常耗时
2、只使用 特征点，丢弃了大部分 可能有用的图像信息
3、无明显纹理信息的地方(白墙、空走廊)，无法匹配

改进思路：

直接法不保留特征点

特征点法 估计 相机运动： 最小化 重投影误差(Reprojection error)
直接法：最小化 光度误差(Photometric error)。根据 像素的亮度信息估计相机运动

特征点法： 只能重构稀疏地图
直接法： 稀疏、稠密、半稠密

8.2 光流

直接法 从 光流 演变
同：相同的假设条件
异：光流描述了像素在图像中的运动，直接法附带一个相机模型。

光流： 描述 像素 随时间 在图像之间运动的方法

稀疏光流： 计算部分像素运动。 Lucas-Kanade光流 【LK光流】
稠密光流： 计算所有像素。 Horn-Schunck光流

所有算法都是在一定假设下工作的。

LK 光流 常被用来 跟踪角点的运动。

8.3 实践： LK 光流 【Code】

8.3.2 用高斯牛顿法 实现光流

本讲 CMakeLists.txt

cmake_minimum_required(VERSION 2.8)
project(ch8)

set(CMAKE_BUILD_TYPE "Release")
add_definitions("-DENABLE_SSE")
set(CMAKE_CXX_FLAGS "-std=c++11 ${SSE_FLAGS} -g -O3 -march=native")

find_package(OpenCV 4 REQUIRED)
find_package(Sophus REQUIRED)
find_package(Pangolin REQUIRED)

include_directories(
        ${OpenCV_INCLUDE_DIRS}
        ${G2O_INCLUDE_DIRS}
        ${Sophus_INCLUDE_DIRS}
        "/usr/include/eigen3/"
        ${Pangolin_INCLUDE_DIRS}
)


add_executable(optical_flow optical_flow.cpp)
target_link_libraries(optical_flow ${OpenCV_LIBS})

#[[   # 块注释
add_executable(direct_method direct_method.cpp)
target_link_libraries(direct_method ${OpenCV_LIBS} ${Pangolin_LIBRARIES} ${Sophus_LIBRARIES})
]]

报错：

/home/xixi/Downloads/slambook2-master/ch8/optical_flow.cpp:145:37: error: ‘CV_GRAY2BGR’ was not declared in this scope
  145 |     cv::cvtColor(img2, img2_single, CV_GRAY2BGR);

改为 cv::COLOR_GRAY2BGR。有3个地方

要是 cd build 还要改图片路径。

mkdir build && cd build 
cmake ..
make 
./optical_flow

optical_flow.cpp

//
// Created by Xiang on 2017/12/19.
//

#include 
#include 
#include 
#include 
#include 

using namespace std;
using namespace cv;

string file_1 = "../LK1.png";  // first image
string file_2 = "../LK2.png";  // second image

/// Optical flow tracker and interface
class OpticalFlowTracker {
public:
    OpticalFlowTracker(
        const Mat &img1_,
        const Mat &img2_,
        const vector<KeyPoint> &kp1_,
        vector<KeyPoint> &kp2_,
        vector<bool> &success_,
        bool inverse_ = true, bool has_initial_ = false) :
        img1(img1_), img2(img2_), kp1(kp1_), kp2(kp2_), success(success_), inverse(inverse_),
        has_initial(has_initial_) {}

    void calculateOpticalFlow(const Range &range);

private:
    const Mat &img1;
    const Mat &img2;
    const vector<KeyPoint> &kp1;
    vector<KeyPoint> &kp2;
    vector<bool> &success;
    bool inverse = true;
    bool has_initial = false;
};

/**
 * single level optical flow
 * @param [in] img1 the first image
 * @param [in] img2 the second image
 * @param [in] kp1 keypoints in img1
 * @param [in|out] kp2 keypoints in img2, if empty, use initial guess in kp1
 * @param [out] success true if a keypoint is tracked successfully
 * @param [in] inverse use inverse formulation?
 */
void OpticalFlowSingleLevel(
    const Mat &img1,
    const Mat &img2,
    const vector<KeyPoint> &kp1,
    vector<KeyPoint> &kp2,
    vector<bool> &success,
    bool inverse = false,
    bool has_initial_guess = false
);

/**
 * multi level optical flow, scale of pyramid is set to 2 by default
 * the image pyramid will be create inside the function
 * @param [in] img1 the first pyramid
 * @param [in] img2 the second pyramid
 * @param [in] kp1 keypoints in img1
 * @param [out] kp2 keypoints in img2
 * @param [out] success true if a keypoint is tracked successfully
 * @param [in] inverse set true to enable inverse formulation
 */
void OpticalFlowMultiLevel(
    const Mat &img1,
    const Mat &img2,
    const vector<KeyPoint> &kp1,
    vector<KeyPoint> &kp2,
    vector<bool> &success,
    bool inverse = false
);

/**
 * get a gray scale value from reference image (bi-linear interpolated)
 * @param img
 * @param x
 * @param y
 * @return the interpolated value of this pixel
 */

inline float GetPixelValue(const cv::Mat &img, float x, float y) {
    // boundary check
    if (x < 0) x = 0;
    if (y < 0) y = 0;
    if (x >= img.cols - 1) x = img.cols - 2;
    if (y >= img.rows - 1) y = img.rows - 2;
    
    float xx = x - floor(x);
    float yy = y - floor(y);
    int x_a1 = std::min(img.cols - 1, int(x) + 1);
    int y_a1 = std::min(img.rows - 1, int(y) + 1);
    
    return (1 - xx) * (1 - yy) * img.at<uchar>(y, x)
    + xx * (1 - yy) * img.at<uchar>(y, x_a1)
    + (1 - xx) * yy * img.at<uchar>(y_a1, x)
    + xx * yy * img.at<uchar>(y_a1, x_a1);
}

int main(int argc, char **argv) {

    // images, note they are CV_8UC1, not CV_8UC3
    Mat img1 = imread(file_1, 0);
    Mat img2 = imread(file_2, 0);

    // key points, using GFTT here.
    vector<KeyPoint> kp1;
    Ptr<GFTTDetector> detector = GFTTDetector::create(500, 0.01, 20); // maximum 500 keypoints
    detector->detect(img1, kp1);

    // now lets track these key points in the second image
    // first use single level LK in the validation picture
    vector<KeyPoint> kp2_single;
    vector<bool> success_single;
    OpticalFlowSingleLevel(img1, img2, kp1, kp2_single, success_single);

    // then test multi-level LK
    vector<KeyPoint> kp2_multi;
    vector<bool> success_multi;
    chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
    OpticalFlowMultiLevel(img1, img2, kp1, kp2_multi, success_multi, true);
    chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
    auto time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
    cout << "optical flow by gauss-newton: " << time_used.count() << endl;

    // use opencv's flow for validation
    vector<Point2f> pt1, pt2;
    for (auto &kp: kp1) pt1.push_back(kp.pt);
    vector<uchar> status;
    vector<float> error;
    t1 = chrono::steady_clock::now();
    cv::calcOpticalFlowPyrLK(img1, img2, pt1, pt2, status, error);
    t2 = chrono::steady_clock::now();
    time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
    cout << "optical flow by opencv: " << time_used.count() << endl;

    // plot the differences of those functions
    Mat img2_single;
    cv::cvtColor(img2, img2_single, cv::COLOR_GRAY2BGR);
    for (int i = 0; i < kp2_single.size(); i++) {
        if (success_single[i]) {
            cv::circle(img2_single, kp2_single[i].pt, 2, cv::Scalar(0, 250, 0), 2);
            cv::line(img2_single, kp1[i].pt, kp2_single[i].pt, cv::Scalar(0, 250, 0));
        }
    }

    Mat img2_multi;
    cv::cvtColor(img2, img2_multi, cv::COLOR_GRAY2BGR);
    for (int i = 0; i < kp2_multi.size(); i++) {
        if (success_multi[i]) {
            cv::circle(img2_multi, kp2_multi[i].pt, 2, cv::Scalar(0, 250, 0), 2);
            cv::line(img2_multi, kp1[i].pt, kp2_multi[i].pt, cv::Scalar(0, 250, 0));
        }
    }

    Mat img2_CV;
    cv::cvtColor(img2, img2_CV, cv::COLOR_GRAY2BGR);
    for (int i = 0; i < pt2.size(); i++) {
        if (status[i]) {
            cv::circle(img2_CV, pt2[i], 2, cv::Scalar(0, 250, 0), 2);
            cv::line(img2_CV, pt1[i], pt2[i], cv::Scalar(0, 250, 0));
        }
    }

    cv::imshow("tracked single level", img2_single);
    cv::imshow("tracked multi level", img2_multi);
    cv::imshow("tracked by opencv", img2_CV);
    cv::waitKey(0);

    return 0;
}

void OpticalFlowSingleLevel(
    const Mat &img1,
    const Mat &img2,
    const vector<KeyPoint> &kp1,
    vector<KeyPoint> &kp2,
    vector<bool> &success,
    bool inverse, bool has_initial) {
    kp2.resize(kp1.size());
    success.resize(kp1.size());
    OpticalFlowTracker tracker(img1, img2, kp1, kp2, success, inverse, has_initial);
    parallel_for_(Range(0, kp1.size()),
                  std::bind(&OpticalFlowTracker::calculateOpticalFlow, &tracker, placeholders::_1));
}

void OpticalFlowTracker::calculateOpticalFlow(const Range &range) {
    // parameters
    int half_patch_size = 4;
    int iterations = 10;
    for (size_t i = range.start; i < range.end; i++) {
        auto kp = kp1[i];
        double dx = 0, dy = 0; // dx,dy need to be estimated
        if (has_initial) {
            dx = kp2[i].pt.x - kp.pt.x;
            dy = kp2[i].pt.y - kp.pt.y;
        }

        double cost = 0, lastCost = 0;
        bool succ = true; // indicate if this point succeeded

        // Gauss-Newton iterations
        Eigen::Matrix2d H = Eigen::Matrix2d::Zero();    // hessian
        Eigen::Vector2d b = Eigen::Vector2d::Zero();    // bias
        Eigen::Vector2d J;  // jacobian
        for (int iter = 0; iter < iterations; iter++) {
            if (inverse == false) {
                H = Eigen::Matrix2d::Zero();
                b = Eigen::Vector2d::Zero();
            } else {
                // only reset b
                b = Eigen::Vector2d::Zero();
            }

            cost = 0;

            // compute cost and jacobian
            for (int x = -half_patch_size; x < half_patch_size; x++)
                for (int y = -half_patch_size; y < half_patch_size; y++) {
                    double error = GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y) -
                                   GetPixelValue(img2, kp.pt.x + x + dx, kp.pt.y + y + dy);;  // Jacobian
                    if (inverse == false) {
                        J = -1.0 * Eigen::Vector2d(
                            0.5 * (GetPixelValue(img2, kp.pt.x + dx + x + 1, kp.pt.y + dy + y) -
                                   GetPixelValue(img2, kp.pt.x + dx + x - 1, kp.pt.y + dy + y)),
                            0.5 * (GetPixelValue(img2, kp.pt.x + dx + x, kp.pt.y + dy + y + 1) -
                                   GetPixelValue(img2, kp.pt.x + dx + x, kp.pt.y + dy + y - 1))
                        );
                    } else if (iter == 0) {
                        // in inverse mode, J keeps same for all iterations
                        // NOTE this J does not change when dx, dy is updated, so we can store it and only compute error
                        J = -1.0 * Eigen::Vector2d(
                            0.5 * (GetPixelValue(img1, kp.pt.x + x + 1, kp.pt.y + y) -
                                   GetPixelValue(img1, kp.pt.x + x - 1, kp.pt.y + y)),
                            0.5 * (GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y + 1) -
                                   GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y - 1))
                        );
                    }
                    // compute H, b and set cost;
                    b += -error * J;
                    cost += error * error;
                    if (inverse == false || iter == 0) {
                        // also update H
                        H += J * J.transpose();
                    }
                }

            // compute update
            Eigen::Vector2d update = H.ldlt().solve(b);

            if (std::isnan(update[0])) {
                // sometimes occurred when we have a black or white patch and H is irreversible
                cout << "update is nan" << endl;
                succ = false;
                break;
            }

            if (iter > 0 && cost > lastCost) {
                break;
            }

            // update dx, dy
            dx += update[0];
            dy += update[1];
            lastCost = cost;
            succ = true;

            if (update.norm() < 1e-2) {
                // converge
                break;
            }
        }

        success[i] = succ;

        // set kp2
        kp2[i].pt = kp.pt + Point2f(dx, dy);
    }
}

void OpticalFlowMultiLevel(
    const Mat &img1,
    const Mat &img2,
    const vector<KeyPoint> &kp1,
    vector<KeyPoint> &kp2,
    vector<bool> &success,
    bool inverse) {

    // parameters
    int pyramids = 4;
    double pyramid_scale = 0.5;
    double scales[] = {1.0, 0.5, 0.25, 0.125};

    // create pyramids
    chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
    vector<Mat> pyr1, pyr2; // image pyramids
    for (int i = 0; i < pyramids; i++) {
        if (i == 0) {
            pyr1.push_back(img1);
            pyr2.push_back(img2);
        } else {
            Mat img1_pyr, img2_pyr;
            cv::resize(pyr1[i - 1], img1_pyr,
                       cv::Size(pyr1[i - 1].cols * pyramid_scale, pyr1[i - 1].rows * pyramid_scale));
            cv::resize(pyr2[i - 1], img2_pyr,
                       cv::Size(pyr2[i - 1].cols * pyramid_scale, pyr2[i - 1].rows * pyramid_scale));
            pyr1.push_back(img1_pyr);
            pyr2.push_back(img2_pyr);
        }
    }
    chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
    auto time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
    cout << "build pyramid time: " << time_used.count() << endl;

    // coarse-to-fine LK tracking in pyramids
    vector<KeyPoint> kp1_pyr, kp2_pyr;
    for (auto &kp:kp1) {
        auto kp_top = kp;
        kp_top.pt *= scales[pyramids - 1];
        kp1_pyr.push_back(kp_top);
        kp2_pyr.push_back(kp_top);
    }

    for (int level = pyramids - 1; level >= 0; level--) {
        // from coarse to fine
        success.clear();
        t1 = chrono::steady_clock::now();
        OpticalFlowSingleLevel(pyr1[level], pyr2[level], kp1_pyr, kp2_pyr, success, inverse, true);
        t2 = chrono::steady_clock::now();
        auto time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
        cout << "track pyr " << level << " cost time: " << time_used.count() << endl;

        if (level > 0) {
            for (auto &kp: kp1_pyr)
                kp.pt /= pyramid_scale;
            for (auto &kp: kp2_pyr)
                kp.pt /= pyramid_scale;
        }
    }

    for (auto &kp: kp2_pyr)
        kp2.push_back(kp);
}

8.4 直接法

光流： 首先追踪特征点位置，再根据这些位置确定相机的运动

• 很难保证全局的最优性。

——> 在后一步中，调整前一步的结果。

稀疏直接法：关键点，假设周围像素不变(因此不必计算描述子)。可快速求解相机位姿。
半稠密直接法：只使用带有梯度的像素点
稠密直接法：多数需要GPU加速

8.5 实践： 双目的稀疏直接法 【Code】

基于特征点的深度恢复(三角化)
基于块匹配的深度恢复

多层直接法 金字塔式

输出： 每个图像的每层金字塔上的追踪点，并输出运行时间。

源码改动：
1、
所有 SE3d 去掉 d

2、改路径
3、报错3

/home/xixi/Downloads/slambook2-master/ch8/direct_method.cpp:206:35: error: ‘CV_GRAY2BGR’ was not declared in this scope
  206 |     cv::cvtColor(img2, img2_show, CV_GRAY2BGR);

改为 cv::COLOR_GRAY2BGR。有3个地方

4、报错4

/usr/bin/ld: CMakeFiles/direct_method.dir/direct_method.cpp.o: in function `JacobianAccumulator::accumulate_jacobian(cv::Range const&)':
/home/xixi/Downloads/slambook2-master/ch8/direct_method.cpp:235: undefined reference to `Sophus::SE3::operator*(Eigen::Matrix<double, 3, 1, 0, 3, 1> const&) const'
/usr/bin/ld: CMakeFiles/direct_method.dir/direct_method.cpp.o: in function `DirectPoseEstimationSingleLayer(cv::Mat const&, cv::Mat const&, std::vector, Eigen::aligned_allocator > > const&, std::vector >, Sophus::SE3&)':
/home/xixi/Downloads/slambook2-master/ch8/direct_method.cpp:178: undefined reference to `Sophus::SE3::exp(Eigen::Matrix<double, 6, 1, 0, 6, 1> const&)'
/usr/bin/ld: /home/xixi/Downloads/slambook2-master/ch8/direct_method.cpp:178: undefined reference to `Sophus::SE3::operator*(Sophus::SE3 const&) const'

Sophus库链接问题

add_executable(direct_method direct_method.cpp)
target_link_libraries(direct_method ${OpenCV_LIBS} ${Pangolin_LIBRARIES} ${Sophus_LIBRARIES})

byzanz-record -x 146 -y 104 -w 786 -h 533  -d 20 --delay=5 -c  /home/xixi/myGIF/test.gif

这里程序运行感觉不太对，暂时不清楚哪里。

direct_method.cpp

#include 
#include 
#include 
#include 

using namespace std;

typedef vector<Eigen::Vector2d, Eigen::aligned_allocator<Eigen::Vector2d>> VecVector2d;

// Camera intrinsics
double fx = 718.856, fy = 718.856, cx = 607.1928, cy = 185.2157;
// baseline
double baseline = 0.573;
// paths
string left_file = "../left.png";
string disparity_file = "../disparity.png";
boost::format fmt_others("../%06d.png");    // other files

// useful typedefs
typedef Eigen::Matrix<double, 6, 6> Matrix6d;
typedef Eigen::Matrix<double, 2, 6> Matrix26d;
typedef Eigen::Matrix<double, 6, 1> Vector6d;

/// class for accumulator jacobians in parallel
class JacobianAccumulator {
public:
    JacobianAccumulator(
        const cv::Mat &img1_,
        const cv::Mat &img2_,
        const VecVector2d &px_ref_,
        const vector<double> depth_ref_,
        Sophus::SE3 &T21_) :
        img1(img1_), img2(img2_), px_ref(px_ref_), depth_ref(depth_ref_), T21(T21_) {
        projection = VecVector2d(px_ref.size(), Eigen::Vector2d(0, 0));
    }

    /// accumulate jacobians in a range
    void accumulate_jacobian(const cv::Range &range);

    /// get hessian matrix
    Matrix6d hessian() const { return H; }

    /// get bias
    Vector6d bias() const { return b; }

    /// get total cost
    double cost_func() const { return cost; }

    /// get projected points
    VecVector2d projected_points() const { return projection; }

    /// reset h, b, cost to zero
    void reset() {
        H = Matrix6d::Zero();
        b = Vector6d::Zero();
        cost = 0;
    }

private:
    const cv::Mat &img1;
    const cv::Mat &img2;
    const VecVector2d &px_ref;
    const vector<double> depth_ref;
    Sophus::SE3 &T21;
    VecVector2d projection; // projected points

    std::mutex hessian_mutex;
    Matrix6d H = Matrix6d::Zero();
    Vector6d b = Vector6d::Zero();
    double cost = 0;
};

/**
 * pose estimation using direct method
 * @param img1
 * @param img2
 * @param px_ref
 * @param depth_ref
 * @param T21
 */
void DirectPoseEstimationMultiLayer(
    const cv::Mat &img1,
    const cv::Mat &img2,
    const VecVector2d &px_ref,
    const vector<double> depth_ref,
    Sophus::SE3 &T21
);

/**
 * pose estimation using direct method
 * @param img1
 * @param img2
 * @param px_ref
 * @param depth_ref
 * @param T21
 */
void DirectPoseEstimationSingleLayer(
    const cv::Mat &img1,
    const cv::Mat &img2,
    const VecVector2d &px_ref,
    const vector<double> depth_ref,
    Sophus::SE3 &T21
);

// bilinear interpolation
inline float GetPixelValue(const cv::Mat &img, float x, float y) {
    // boundary check
    if (x < 0) x = 0;
    if (y < 0) y = 0;
    if (x >= img.cols) x = img.cols - 1;
    if (y >= img.rows) y = img.rows - 1;
    uchar *data = &img.data[int(y) * img.step + int(x)];
    float xx = x - floor(x);
    float yy = y - floor(y);
    return float(
        (1 - xx) * (1 - yy) * data[0] +
        xx * (1 - yy) * data[1] +
        (1 - xx) * yy * data[img.step] +
        xx * yy * data[img.step + 1]
    );
}

int main(int argc, char **argv) {

    cv::Mat left_img = cv::imread(left_file, 0);
    cv::Mat disparity_img = cv::imread(disparity_file, 0);

    // let's randomly pick pixels in the first image and generate some 3d points in the first image's frame
    cv::RNG rng;
    int nPoints = 2000;
    int boarder = 20;
    VecVector2d pixels_ref;
    vector<double> depth_ref;

    // generate pixels in ref and load depth data
    for (int i = 0; i < nPoints; i++) {
        int x = rng.uniform(boarder, left_img.cols - boarder);  // don't pick pixels close to boarder
        int y = rng.uniform(boarder, left_img.rows - boarder);  // don't pick pixels close to boarder
        int disparity = disparity_img.at<uchar>(y, x);
        double depth = fx * baseline / disparity; // you know this is disparity to depth
        depth_ref.push_back(depth);
        pixels_ref.push_back(Eigen::Vector2d(x, y));
    }

    // estimates 01~05.png's pose using this information
    Sophus::SE3 T_cur_ref;

    for (int i = 1; i < 6; i++) {  // 1~10
        cv::Mat img = cv::imread((fmt_others % i).str(), 0);
        // try single layer by uncomment this line
        // DirectPoseEstimationSingleLayer(left_img, img, pixels_ref, depth_ref, T_cur_ref);
        DirectPoseEstimationMultiLayer(left_img, img, pixels_ref, depth_ref, T_cur_ref);
    }
    return 0;
}

void DirectPoseEstimationSingleLayer(
    const cv::Mat &img1,
    const cv::Mat &img2,
    const VecVector2d &px_ref,
    const vector<double> depth_ref,
    Sophus::SE3 &T21) {

    const int iterations = 10;
    double cost = 0, lastCost = 0;
    auto t1 = chrono::steady_clock::now();
    JacobianAccumulator jaco_accu(img1, img2, px_ref, depth_ref, T21);

    for (int iter = 0; iter < iterations; iter++) {
        jaco_accu.reset();
        cv::parallel_for_(cv::Range(0, px_ref.size()),
                          std::bind(&JacobianAccumulator::accumulate_jacobian, &jaco_accu, std::placeholders::_1));
        Matrix6d H = jaco_accu.hessian();
        Vector6d b = jaco_accu.bias();

        // solve update and put it into estimation
        Vector6d update = H.ldlt().solve(b);;
        T21 = Sophus::SE3::exp(update) * T21;
        cost = jaco_accu.cost_func();

        if (std::isnan(update[0])) {
            // sometimes occurred when we have a black or white patch and H is irreversible
            cout << "update is nan" << endl;
            break;
        }
        if (iter > 0 && cost > lastCost) {
            cout << "cost increased: " << cost << ", " << lastCost << endl;
            break;
        }
        if (update.norm() < 1e-3) {
            // converge
            break;
        }

        lastCost = cost;
        cout << "iteration: " << iter << ", cost: " << cost << endl;
    }

    cout << "T21 = \n" << T21.matrix() << endl;
    auto t2 = chrono::steady_clock::now();
    auto time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
    cout << "direct method for single layer: " << time_used.count() << endl;

    // plot the projected pixels here
    cv::Mat img2_show;
    cv::cvtColor(img2, img2_show, cv::COLOR_GRAY2BGR);
    VecVector2d projection = jaco_accu.projected_points();
    for (size_t i = 0; i < px_ref.size(); ++i) {
        auto p_ref = px_ref[i];
        auto p_cur = projection[i];
        if (p_cur[0] > 0 && p_cur[1] > 0) {
            cv::circle(img2_show, cv::Point2f(p_cur[0], p_cur[1]), 2, cv::Scalar(0, 250, 0), 2);
            cv::line(img2_show, cv::Point2f(p_ref[0], p_ref[1]), cv::Point2f(p_cur[0], p_cur[1]),
                     cv::Scalar(0, 250, 0));
        }
    }
    cv::imshow("current", img2_show);
    cv::waitKey();
}

void JacobianAccumulator::accumulate_jacobian(const cv::Range &range) {

    // parameters
    const int half_patch_size = 1;
    int cnt_good = 0;
    Matrix6d hessian = Matrix6d::Zero();
    Vector6d bias = Vector6d::Zero();
    double cost_tmp = 0;

    for (size_t i = range.start; i < range.end; i++) {

        // compute the projection in the second image
        Eigen::Vector3d point_ref =
            depth_ref[i] * Eigen::Vector3d((px_ref[i][0] - cx) / fx, (px_ref[i][1] - cy) / fy, 1);
        Eigen::Vector3d point_cur = T21 * point_ref;
        if (point_cur[2] < 0)   // depth invalid
            continue;

        float u = fx * point_cur[0] / point_cur[2] + cx, v = fy * point_cur[1] / point_cur[2] + cy;
        if (u < half_patch_size || u > img2.cols - half_patch_size || v < half_patch_size ||
            v > img2.rows - half_patch_size)
            continue;

        projection[i] = Eigen::Vector2d(u, v);
        double X = point_cur[0], Y = point_cur[1], Z = point_cur[2],
            Z2 = Z * Z, Z_inv = 1.0 / Z, Z2_inv = Z_inv * Z_inv;
        cnt_good++;

        // and compute error and jacobian
        for (int x = -half_patch_size; x <= half_patch_size; x++)
            for (int y = -half_patch_size; y <= half_patch_size; y++) {

                double error = GetPixelValue(img1, px_ref[i][0] + x, px_ref[i][1] + y) -
                               GetPixelValue(img2, u + x, v + y);
                Matrix26d J_pixel_xi;
                Eigen::Vector2d J_img_pixel;

                J_pixel_xi(0, 0) = fx * Z_inv;
                J_pixel_xi(0, 1) = 0;
                J_pixel_xi(0, 2) = -fx * X * Z2_inv;
                J_pixel_xi(0, 3) = -fx * X * Y * Z2_inv;
                J_pixel_xi(0, 4) = fx + fx * X * X * Z2_inv;
                J_pixel_xi(0, 5) = -fx * Y * Z_inv;

                J_pixel_xi(1, 0) = 0;
                J_pixel_xi(1, 1) = fy * Z_inv;
                J_pixel_xi(1, 2) = -fy * Y * Z2_inv;
                J_pixel_xi(1, 3) = -fy - fy * Y * Y * Z2_inv;
                J_pixel_xi(1, 4) = fy * X * Y * Z2_inv;
                J_pixel_xi(1, 5) = fy * X * Z_inv;

                J_img_pixel = Eigen::Vector2d(
                    0.5 * (GetPixelValue(img2, u + 1 + x, v + y) - GetPixelValue(img2, u - 1 + x, v + y)),
                    0.5 * (GetPixelValue(img2, u + x, v + 1 + y) - GetPixelValue(img2, u + x, v - 1 + y))
                );

                // total jacobian
                Vector6d J = -1.0 * (J_img_pixel.transpose() * J_pixel_xi).transpose();

                hessian += J * J.transpose();
                bias += -error * J;
                cost_tmp += error * error;
            }
    }

    if (cnt_good) {
        // set hessian, bias and cost
        unique_lock<mutex> lck(hessian_mutex);
        H += hessian;
        b += bias;
        cost += cost_tmp / cnt_good;
    }
}

void DirectPoseEstimationMultiLayer(
    const cv::Mat &img1,
    const cv::Mat &img2,
    const VecVector2d &px_ref,
    const vector<double> depth_ref,
    Sophus::SE3 &T21) {

    // parameters
    int pyramids = 4;
    double pyramid_scale = 0.5;
    double scales[] = {1.0, 0.5, 0.25, 0.125};

    // create pyramids
    vector<cv::Mat> pyr1, pyr2; // image pyramids
    for (int i = 0; i < pyramids; i++) {
        if (i == 0) {
            pyr1.push_back(img1);
            pyr2.push_back(img2);
        } else {
            cv::Mat img1_pyr, img2_pyr;
            cv::resize(pyr1[i - 1], img1_pyr,
                       cv::Size(pyr1[i - 1].cols * pyramid_scale, pyr1[i - 1].rows * pyramid_scale));
            cv::resize(pyr2[i - 1], img2_pyr,
                       cv::Size(pyr2[i - 1].cols * pyramid_scale, pyr2[i - 1].rows * pyramid_scale));
            pyr1.push_back(img1_pyr);
            pyr2.push_back(img2_pyr);
        }
    }

    double fxG = fx, fyG = fy, cxG = cx, cyG = cy;  // backup the old values
    for (int level = pyramids - 1; level >= 0; level--) {
        VecVector2d px_ref_pyr; // set the keypoints in this pyramid level
        for (auto &px: px_ref) {
            px_ref_pyr.push_back(scales[level] * px);
        }

        // scale fx, fy, cx, cy in different pyramid levels
        fx = fxG * scales[level];
        fy = fyG * scales[level];
        cx = cxG * scales[level];
        cy = cyG * scales[level];
        DirectPoseEstimationSingleLayer(pyr1[level], pyr2[level], px_ref_pyr, depth_ref, T21);
    }

}

8.5.4 直接法的优缺点

优点：
1、省去计算特征点、描述子的时间
2、只要求有像素梯度，不需要特征点，可 在特征缺失的场合使用。
3、可以构建 半稠密 乃至 稠密的地图

缺点：
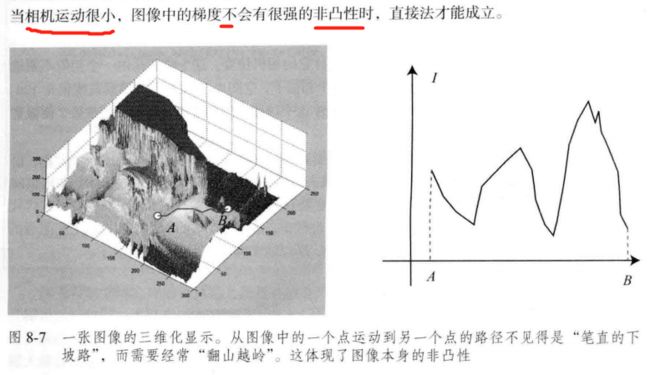
1、图像 强烈非凸。优化算法易进入极小，只有运动很小时直接法才能成功。金字塔的引入可以在一定程度上减小非凸的影响。
2、单个像素无区分度 ——> 图像块 or 相关性。500个点以上
3、强假设： 灰度值不变。 ——> 同时估计相机的曝光参数

习题 8

√ 题1 光流方法

1、除了LK光流，还有哪些光流方法？它们各有什么特点？

文档

稠密光流：

DIS(Dense Inverse Search，稠密逆搜索)光流算法：【低时间复杂度+有竞争力的精度】
DIS光流算法。这个类实现了密集逆搜索(DIS)光流算法。包括三个预设，带有预选参数，在速度和质量之间提供合理的权衡。但是，即使是最慢的预设也还是比较快的，如果你需要更好的质量，不关心速度，可以使用DeepFlow。
Till Kroeger, Radu Timofte, Dengxin Dai, and Luc Van Gool. Fast optical flow using dense inverse search. In Proceedings of the European Conference on Computer Vision (ECCV), 2016.
三部分：

1. inverse search for patch correspondences;
2. dense displacement field creation through patch aggregation along multiple scales; 多尺度斑块聚集 形成 密集位移场;
3. variational refinement.

——————————
cv::FarnebackOpticalFlow
使用Gunnar Farneback算法计算密集光流。

• Two-Frame Motion Estimation Based on
  Polynomial Expansion

——————————
基于鲁棒局部光流(RLOF，robust local optical flow)算法和稀疏到密集插值方案的快速密集光流计算。
有相应的稀疏 API

——————————
“Dual TV L1” Optical Flow Algorithm.

C. Zach, T. Pock and H. Bischof, “A Duality Based Approach for Realtime TV-L1 Optical Flow”. Javier Sanchez, Enric Meinhardt-Llopis and Gabriele Facciolo. “TV-L1 Optical Flow Estimation”.

——————————
【基于翘曲理论的高精度光流估计：角误差更小，对参数变化不敏感，噪声鲁棒】Thomas Brox, Andres Bruhn, Nils Papenberg, and Joachim Weickert. High accuracy optical flow estimation based on a theory for warping. In Computer Vision-ECCV 2004, pages 25–36. Springer, 2004.
将一个连续的、旋转不变的能量泛函，用于光流计算，该泛函基于两个项:一个具有亮度常数和梯度常数假设的鲁棒数据项，结合一个保持不连续的时空 TV 正则化器。

cv::VariationalRefinement::calcUV()

稀疏光流

该类可以使用金字塔迭代Lucas-Kanade方法计算稀疏特征集的光流。

题2

2、 在本节程序的求图像梯度过程中，我们简单地求了 $u+1$ 和 $u-1$ 的灰度之差除以 2，作为 $u$ 方向上的梯度值。这种做法有什么缺点？提示：对于距离较近的特征，变化应该较快；而距离较远的特征在图像中变化较慢，求梯度时能否利用此信息？

题3

3、直接法是否能和光流一样，提出“反向法”的概念？即，使用原始图像的梯度代替目标图像的梯度？

题4

4、使用Ceres或g2o实现稀疏直接法和半稠密直接法。

题5

单目直接法：在优化时 把 像素深度 也作为优化变量