代码随想录 哈希表模块小结
哈希表其实是一种比较好理解的数据结构,重点是要搞清楚哈希表的映射关系,以及对哈希表的实现选型。
哈希表的实现结构主要有三种:
1、hashmap
2、set
3、数组
三种实现方式各有优劣,要根据具体的题目去选择要使用哪一种。
接下来针对不同的题目来判断哈希表的选型问题,以及常见的做法。
一、数组
242. 有效的字母异位词 - 力扣(LeetCode)
383. 赎金信 - 力扣(LeetCode)
这两道题都是以数组作为hash表的实现方式,因为映射方式和表大小都可以提前确定下来。
映射方式:字母与'a'的ACSII码差值作为索引位置下标,存放的值为字母出现的次数,这是天然的映射方式。
表大小:26个字母,且都为小写,那么就有26个ACSII码差值,表大小为26。
两道题非常类似,做法就是先将一个串的的全部字母出现次数保存到表里,再与另一个串的字母出现次数作差,最后判断表的数值情况。
字母异位词代码:
class Solution {
public boolean isAnagram(String s, String t) {
int[] map = new int[26]; // 保存两个数组的字母出现频率
for (int i = 0; i < s.length(); i++) {
map[s.charAt(i) - 'a'] += 1; // 出现就加一次
}
for (int i = 0; i < t.length(); i++) {
map[t.charAt(i) - 'a'] -= 1; // 出现就减一次
}
for (int n : map) {
if (n != 0) return false; // 有任何一个不等于0 说明次数不对 直接返回false
}
return true;
}
}赎金信代码:
class Solution {
public boolean canConstruct(String ransomNote, String magazine) {
// 跟字母异位词一个类型
int[] map = new int[26];
for (int i = 0; i < ransomNote.length(); i++) {
map[ransomNote.charAt(i) - 'a'] += 1;
}
for (int i = 0; i < magazine.length(); i++) {
map[magazine.charAt(i) - 'a'] -= 1;
}
for (int n : map) {
if (n > 0) return false; // 有大于0 的 说明ransomNote里有的字符magazine里没有
}
return true;
}
}二、Set
set作为hash表的实现结构,主要目的就是为了去重。
以LC_349为例
349. 两个数组的交集 - 力扣(LeetCode)
这道题与字母异位词的做法其实也是类似的,但是要统计的结果不能是重复的,因此需要对两个数组的结果都进行去重。
其实用hashmap也可以做,但是这道题不需要保存
代码如下:
class Solution {
public int[] intersection(int[] nums1, int[] nums2) {
HashSet numSet = new HashSet(); // 使用set去重
HashSet resSet = new HashSet();
for (int n : nums1) {
numSet.add(n); // 先记录nums1有哪些元素
}
for (int n : nums2) {
if (numSet.contains(n)) { // 再判断nums2里的元素哪些在nums1中
resSet.add(n); // 有就加入结果集
}
}
// 转成数组
int[] res = new int[resSet.size()];
int index = 0;
for (Object o : resSet) {
res[index++] = (int)o;
}
return res;
}
} 三、HashMap
hashmap实现方式应该是用的最多的了,使用的情况主要为了每一个元素需要保存两个或两个以上的值。
1、两数之和
1. 两数之和 - 力扣(LeetCode)
这道题要通过数值去比较,同时要返回其下标,表每个位置保存一个元素肯定不行,所以要保存
hashmap中每个元素为entry,保存<值,对应下标>。
实现思路为,每次遍历都要判断target - nums[i]是否在表里,若在则找到了第二个数,则将target - nums[i]的下标取出来返回。target - nums[i]可以理解为映射关系了。
这道题有一个注意的点,因为题目说了答案唯一,所以不用担心遇到相同元素时会覆盖掉map之前put的结果。
代码如下:
class Solution {
public int[] twoSum(int[] nums, int target) {
HashMap map = new HashMap();
int[] res = new int[2];
for (int i = 0; i < nums.length; i++) {
// 不用担心在找到两个结果数之前 出现两个重复的数会重复放到map中
// 因为题目说了答案唯一 所以一定不会存在这种情况
if (map.containsKey(target - nums[i])) {
res[0] = i;
res[1] = map.get(target - nums[i]);
break;
}
map.put(nums[i], i);
}
return res;
}
} 2、四数相加II
454. 四数相加 II - 力扣(LeetCode)
这道题要统计四元组出现次数,也可以通过hashmap来实现,
k保存数值,v保存次数。
那么保存什么数值以及什么的次数?
四个数组,总不能处理四次,所以首先想到的是能不能减少处理的次数,或者说看成两个数组来处理。
因此k可以保存两个数组的元素和,v保存对应元素和的出现次数。
本题的解题步骤如下:
- 首先定义一个map,key放a和b两数之和,value放a和b两数之和出现的次数。
- 遍历A和B数组,统计两个数组元素之和,和出现的次数,放到map中。
- 定义int变量count,用来统计 a+b+c+d = 0 出现的次数。
- 在遍历C和D数组,找到如果 0-(c+d) 在map中出现过的话,就用count把map中key对应的value也就是出现次数统计累加出来。
- 最终count就是结果。
这样就相当于处理了两次,每次处理两个数组。
为什么0-(c+d) 在map中出现,count直接累加对应的value值?
因为0-(c+d)意味着有一个组合了,而固定下(c+d)后,可以组成-(a+b)的次数为value次,因此组成 a+b+c+d = 0的次数为value次。
步骤确定下来后,剩下的就是按部就班。
整体代码如下:
class Solution {
public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
// 四个数组转化成两个数组来处理
HashMap map = new HashMap();
int count = 0; // 统计次数
int sum = 0;
int len = nums1.length;
for (int i = 0; i < len; i++) {
for (int j = 0; j < len; j++) {
sum = nums1[i] + nums2[j]; // 枚举元素和
// 统计前两个数组元素和的次数 重复就加1
map.put(sum, map.getOrDefault(sum, 0) + 1);
}
}
for (int i = 0; i < len; i++) {
for (int j = 0; j < len; j++) {
sum = nums3[i] + nums4[j]; // 枚举元素和
// 看看另外两个数组元素和的相反数在不在map里 有就把计数取出来累加
if (map.containsKey(-sum)) count += map.get(-sum);
}
}
return count;
}
} 四、补充题目
15. 三数之和 - 力扣(LeetCode)
这道题个人感觉难度还是比较大的,因为涉及到去重问题,如果用list保存结果,再用set去去重,复杂度较高。
最好的做法是使用双指针,因为是处理同一个数组,效率还是比较高的。
注意,使用双指针法要对数组进行排序。
如果这道题要返回的是数组下标,那么是不能用双指针法去做的。
具体的实现逻辑根据卡哥给的动态图,非常清晰。
数值大小默认是升序。
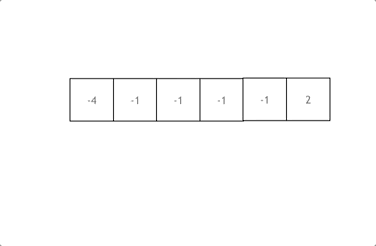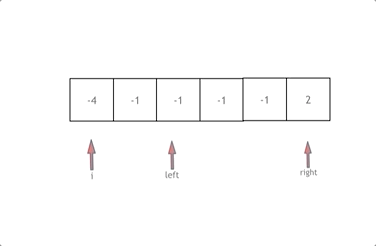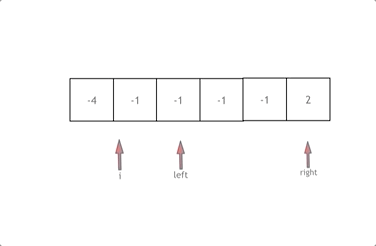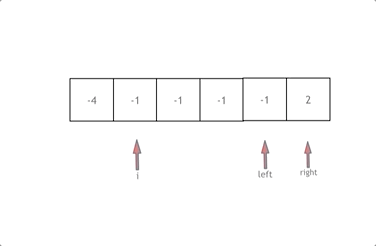
固定一个i,然后让两个指针在i + 1到length - 1的区域进行扫描,确定三元组的组合。
但是题目要求不能出现相同的三元组组合,意味着i以及两个指针的组合是不能重复的。
又因为数组有序,相同的数字是紧挨着的,因此可以通过相邻的数字判断来决定是否选取该数字进行组合。
完整代码如下:
class Solution {
public List> threeSum(int[] nums) {
// 双指针
// 不返回下标 所以可以排序
Arrays.sort(nums);
ArrayList> res = new ArrayList();
for (int i = 0; i < nums.length; i++) {
// 去重 这步很关键
// 1、下一个元素不能与上一个元素相同,若相同,即使后面依然有符合的两个元素,最终组成的也是重复的元组(前面相同的数字已经包含了数字组合)
///2、不能是if (nums[i] == nums[i + 1]) 因为这样可能会漏掉nums[i]这个数字对应的三元组,例如(-1,-1,2)
// 所以必须是先处理过之后 往前面去比较
if (i > 0 && nums[i] == nums[i - 1]) continue;
// 两个指针在i后面的区域扫描
int front = i + 1;
int last = nums.length - 1; // 左闭右闭
while (front < last) { // front 和last不能相等
// 去重不能放这
//while(...)
//while(...)
// 相加小于0 说明要往右走
if (nums[i] + nums[front] + nums[last] < 0) front++;
// 相加大于0 说明要往左走
else if (nums[i] + nums[front] + nums[last] > 0) last--;
else {
// 找到了 添加三元组
res.add(Arrays.asList(nums[i], nums[front], nums[last]));
// 1、下一个元素不能与上一个元素相同 要去重 这步很关键
// 2、去重逻辑应该放在找到了一个三元组之后 很重要,否则会漏掉某些组合,例如(-2,1,1)
while (front < last && nums[front] == nums[front + 1]) front++;
while (front < last && nums[last] == nums[last - 1]) last--;
front++;
last--;
}
}
}
return res;
}
}