【数据挖掘】2、数据预处理
文章目录
- 一、数据预处理的意义
-
- 1.1 缺失数据
-
- 1.1.1 原因
- 1.1.2 方案
- 1.1.3 离群点分析
- 1.2 重复数据
-
- 1.2.1 原因
- 1.2.2 去重的方案
- 1.3 数据转换
- 1.4 数据描述
- 二、数据预处理方法
-
- 2.1 特征选择 Feature Selection
- 2.2 特征提取 Feature Extraction
-
- 2.2.1 PCA 主成分分析
- 2.2.2 LDA 线性判别分析
数据预处理分为数据清洗、转换、描述、选择、提起五部分:
一、数据预处理的意义
数据预处理的意义:因为真实世界的问题,脏数据的预处理才是最大的挑战。脏数据主要包括如下方面:
1.1 缺失数据
1.1.1 原因
可能有很多原因:
- 设备故障
- 并未提供数据(例如调查问卷的被访人)
- 不适用、无意义(可能并无物理意义,比如一张宽表:既有学生、又有教师,那么学生并无收入(只有教师才有),则此表格设计的并不合理)

1.1.2 方案
数据缺失的应对方案:其实是一门艺术
- 忽略:
- 不处理有问题的列或行(当然只有这部分数据较少才可以)
- 填充:
- 重新采集
- 利用领域知识去猜:(比如一个人住了 18 年的房子,那推测为住房,而不是租房形式)
- 用固定值 or 均值、众数等
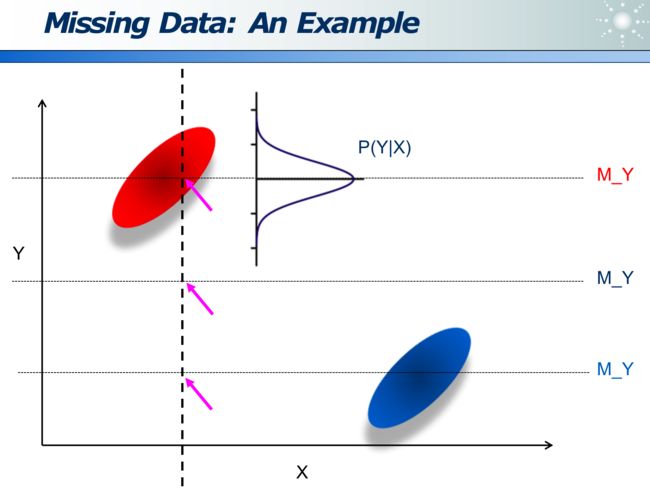
可以在均值基础上,做高斯分布,来让填充的数据即具备随机性,又基于一个基点分布:
Outliers 异常值:是指数据明显出错了
而 Anomaly 指数据是正确的,只是它和众数有别:例如下图中的黄衣服人也是正常的样本,只是他没有和别人聚在一堆而已:
1.1.3 离群点分析
因为离群点是相对概念,所以不能只用绝对距离distance(A, B),而应用相对距离lrd(A)。
那么 LOF(A) 则正比于 lrd(B) / lrd(A)
- 其中
lrd(A)指:待分析的A点,距离其近邻 B 的均值。 - 其中
lrd(B)指:待分析A点 的 近邻点 B,距离其近邻们的均值。 - 若二者之商越大,则说明 A 越「相对」离群。
例如下图是离群点分析的结果:其红色圆圈越大(红圈内的数字即为 LOF 值)则说明越离群
1.2 重复数据
1.2.1 原因
不同数据源汇总时,都包含同一个人的信息,需要汇总。
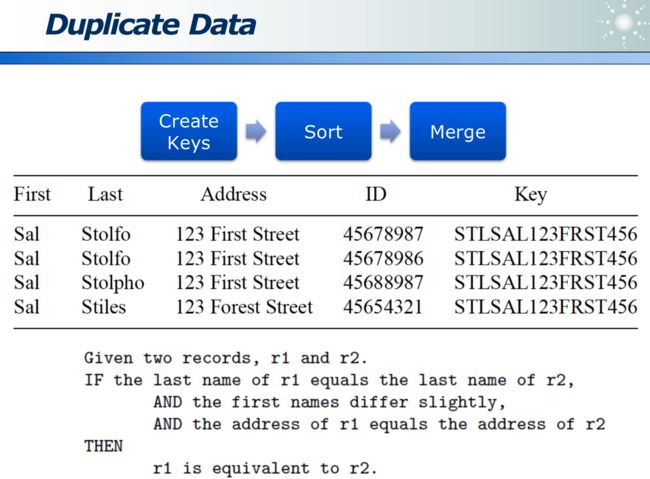
1.2.2 去重的方案
因为大数据,不可能在所有数据范围内去重。因此一般采用局部去重。
- 如果业务决定重复的数据通常相邻,则可用滑动窗口实现(在滑窗内去重):即在一定程度去重,又提升了计算性能。
可以根据领域知识,定义一种规则:来识别出原本相同,但被错记录的数据。比如若名字相同,姓不同,地址相同的人,认为是同一个人。
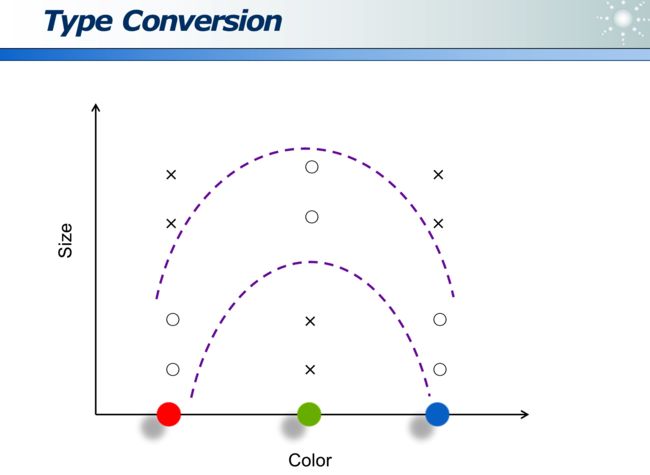
1.3 数据转换
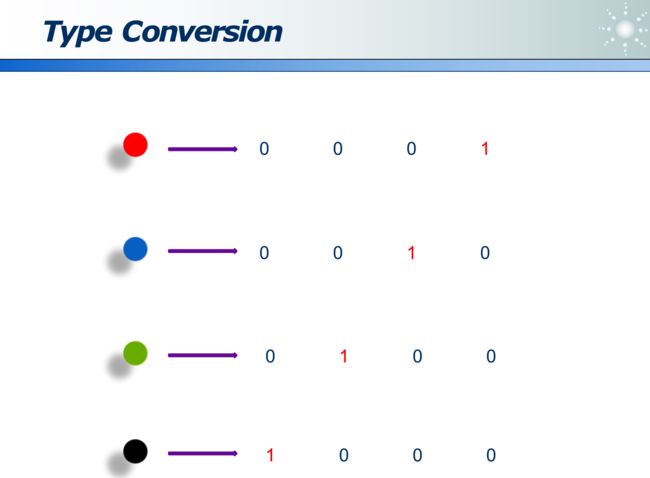
数据的编码:影响数据问题的复杂度
可以用位来标识不同数据:
不平衡数据:当两类数据占比差别很大时,整体准确率并不能很好地度量,应用各自的准确率。(例如 99%人健康,1%的人生病,模型需要预测出生病的人)
G-mean 方法:
采样不均衡:可以有针对性的,对数据量少的类(如下图的蓝色点),多采样。

边缘采样:边缘点的价值更大
归一化:
1.4 数据描述
相关性可用「皮尔森相关系数」衡量,其分子为 「A 与 B 的协方差」,分母为「A的方差 乘以 B的方差」
- ra,b > 0:正相关:即 a 越大则 b 越大,即 a 与 b 的协方差为正
- ra,b = 0:没有「线性」相关性
- ra,b > 0:负相关:即 a 越大则 b 越小,即 a 与 b 的协方差为负

要理解 Pearson 相关系数,首先要理解协方差(Covariance)。协方差表示两个变量 X,Y 间相互关系的数字特征,其计算公式为:
协方差公式如下:
C o v ( X , Y ) = 1 n − 1 Σ 1 n ( X i − X ‾ ) ( Y i − Y ‾ ) Cov(X,Y)=\frac{1}{n-1}\Sigma_1^n \ (X_i-\overline X)(Y_i-\overline Y) Cov(X,Y)=n−11Σ1n (Xi−X)(Yi−Y)
当 Y = X 时,即与方差相同。当变量 X,Y 的变化趋势一致时,Pearson 相关系数为正数。当变量 X,Y 的变化趋势相反时,Pearson 相关系数为负数。
Pearson 相关系数如下:
C O R ( X , Y ) = Σ 1 n ( X i − X ‾ ) ( Y i − Y ‾ ) Σ 1 n ( X i − X ‾ ) 2 Σ 1 n ( Y i − Y ‾ ) 2 COR(X, Y) = \frac{\Sigma_1^n(X_i-\overline X)(Y_i-\overline Y)}{\sqrt{\Sigma_1^n(X_i-\overline X)^2\Sigma_1^n(Y_i-\overline Y)^2}} COR(X,Y)=Σ1n(Xi−X)2Σ1n(Yi−Y)2Σ1n(Xi−X)(Yi−Y)
由公式可知,Pearson 相关系数是用协方差除以两个变量的标准差得到的,虽然协方差能反映两个随机变量的相关程度(协方差大于0的时候表示两者正相关,小于0的时候表示两者负相关),但其数值上受量纲的影响很大,不能简单地从协方差的数值大小给出变量相关程度的判断。为了消除这种量纲的影响,于是就有了相关系数的概念。
当两个变量的方差都不为零时,相关系数才有意义,相关系数的取值范围为[-1,1]。

计算方式为cor = corr(Matrix,'type','Pearson'),其中Matrix 参数即为需要计算的矩阵。
数据相关性描述:Person 卡方检定,其值越大则相关性越大(如下图为 507.93 较大,说明有较大相关性)
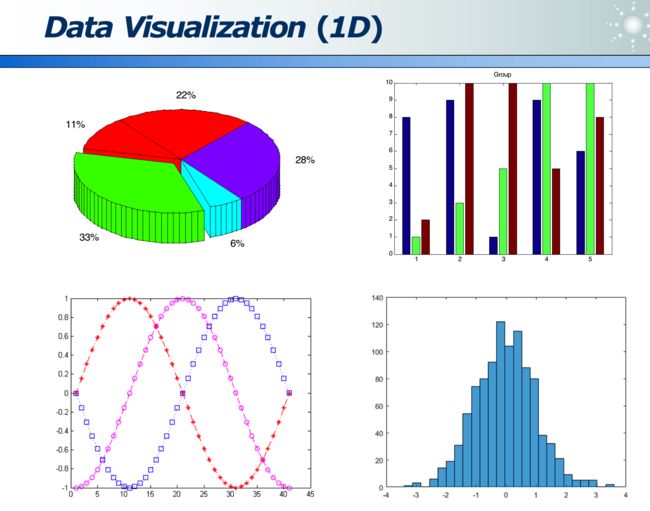
数据可视化:
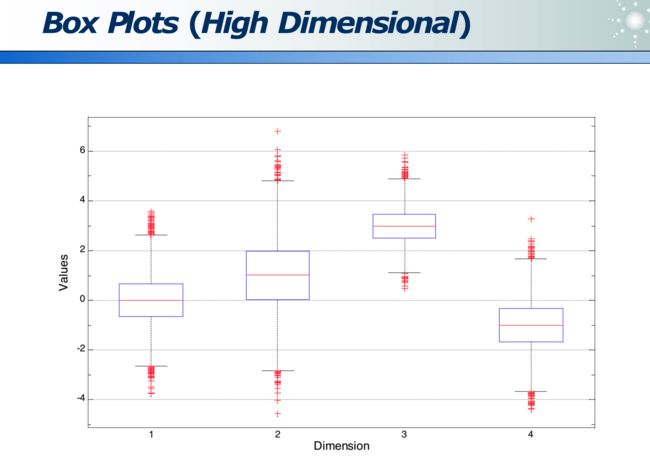
高维数据:各维度的分布
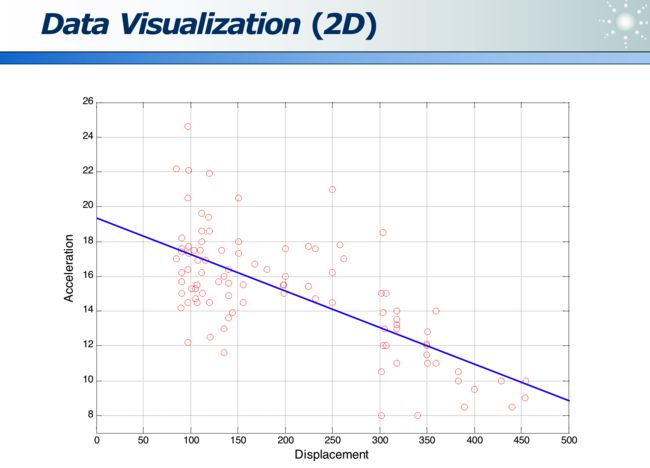
高维数据:各位数据的关系
CiteSpace 是文献可视化的软件:下图为文章的引用次数
Gephi 软件可以可视化各维度数据,是开源的:
二、数据预处理方法
2.1 特征选择 Feature Selection
收集到大量的特征,需要选择好的、有代表性的特征,这个过程称为特征选择。
下图是指:身高的分布,其中 Class A 是女生身高分布曲线,Class B 是男生身高分布曲线:

下图是抽烟的数据集:其中 60% 不抽烟,40% 抽烟。不抽烟的人由 60% 女 + 40% 男构成。抽烟的人由 5% 女 + 95% 男构成。
熵:可以量化属性的区分度
- 1 就是最大的熵,表示最不确定。
- 属性整体的效能是 0.5477
- 此属性的信息增益(Information Gain)是 1 - 0.5477 = 0.4523,表示此属性的价值。此值越大,说明此属性的效力越高(因为将原来最不确定性的熵降低的幅度最大)。

利用熵,在各种属性里搜索,最好的属性。
- 利用 Branch and Bound 可以剪枝
2.2 特征提取 Feature Extraction
特征提取:是指对特征做一定转换,如下图将像素点转变为像素点的差值,来分割边缘。
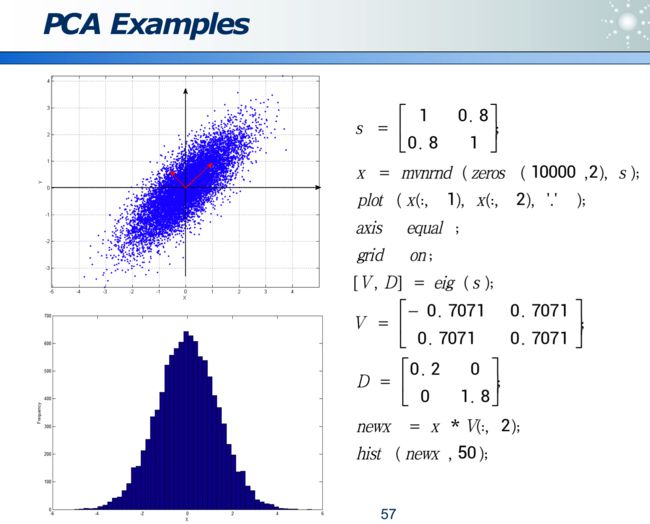
2.2.1 PCA 主成分分析
事物从不同角度看,不同的映射方法,信息损失程度不同:
如果某属性区分度越大,则此属性越重要。
可以经过变换来消除 correlation,使更容易选特征:
2.2.2 LDA 线性判别分析
PCA 虽然计算量不大,但如果投影方向选错,会丢失类别信息,使得无法区分主成分:
- 如下图如果延着长的红色箭头投影,则蓝黄两类在投影线上无法区分
- 如下图如果延着短的红色箭头投影,则蓝黄两类在投影线上可以区分
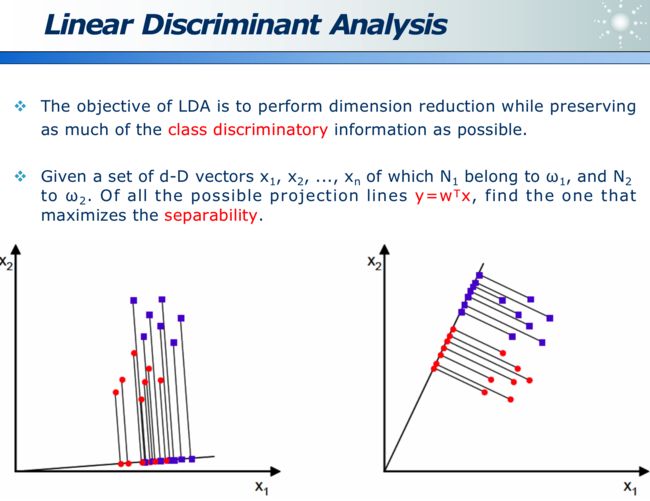
LDA 的目的就是,在维度收缩时,尽量保留「类间区分度」信息,如下图,x 为原始数据, w 即为方向,降为数据 y,左图区分度小,而右图区分度大即效果好。
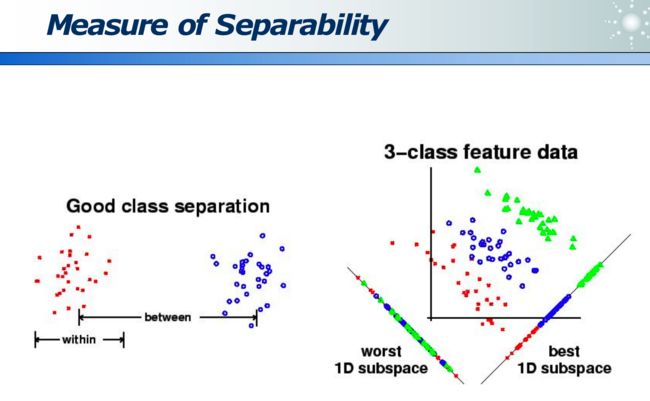
类间距离大,而类内距离小:
投影评价的准则是 J J J最大化: J = ∣ μ 1 − μ 2 ∣ 2 S 1 2 + S 2 2 J=\frac{\left|\mu_1-\mu_2\right|^2}{S_1^2+S_2^2} J=S12+S22∣μ1−μ2∣2
其中分子是「类间距离」越大越好,分母是「类内距离」越小越好:
多类分类问题: