【Acwing提高】DP·背包

推荐：炒鸡棒的适合萌新的DP题单（大概？）

【Acwing提高】DP·背包

知识点

题目	扩展方式	扩展来源
采药	裸的	01
装箱问题	价值=体积，最小转求最大	01
宠物小精灵之收服	价值为1，费用不为0，多关键字	01二维费用
数字组合	费用恰好，求方案数	01
买书	费用恰好，求方案数	完全背包
货币系统1021	求方案数，开longlong	完全背包
货币系统531	求方案数，模型转化，可行性	完全背包
多重背包问题 III	单调队列优化（滑动窗口）	多重
庆功会	裸的	多重背包
混合背包问题	大杂烩	01，多重，完全
二维费用的背包问题	二维费用	01
潜水员	费用变为至少，求min	二维费用01
机器分配	抽象转化，求具体方案	分组背包
开心的金明	裸的	01
有依赖的背包问题	树形依赖	树形dp，分组，金明的预算方案
背包问题求方案数	最优解方案数（最短路条数），体积恰好	01
背包问题求具体方案	物品逆向，字典序最小（贪心，求具体方案）	01
能量石	贪心	01
金明的预算方案	有依赖背包，两层依赖	分组

题目

采药

思路
裸的01没啥好讲的，但是这里代码写的比自己的好，因为边输入边计算，节省空间了
代码

#include
using namespace std;
typedef long long ll;
int n,m,v,w;
const int N=1005;
ll f[N];

int main()
{
    cin>>m>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>v>>w;//输入同时计算
        for(int j=m;j>=v;j--)f[j]=max(f[j],f[j-v]+w);
    }
    cout<<f[m];
    return 0;
}

装箱问题

思路
价值=体积，最小转求最大
代码

#include
using namespace std;
typedef long long ll;
int n,m,v;
const int N=2e4+10;
ll f[N];

int main()
{
    cin>>m>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>v;
        for(int j=m;j>=v;j--)f[j]=max(f[j],f[j-v]+v);
    }
    cout<<m-f[m];
    return 0;
}

宠物小精灵之收服

思路
捕获精灵数越多越好，如果相同，剩余体力越多越好

捕获精灵数越多越好
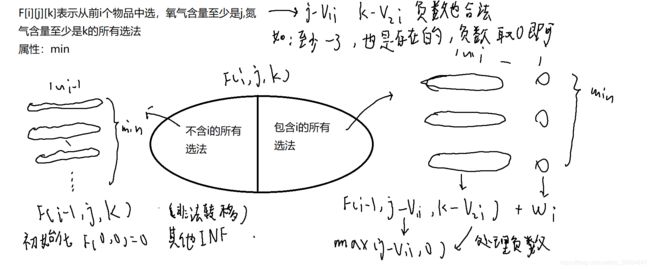
二维费用背包（具体推导看后面题目），价值为1，体力值不能为0是需要注意的点

同时，对于背包问题，体积和价值是可以互换的，因此根据数据范围选择体积和价值可以有效地降低时间复杂度
另外一种题解：(体力、精灵数为费用，精灵球数为价值) $O(K^{2}M)$

剩余体力越多越好找到最小的k使得$f[V_1][k]==f[V_1][V_2-1]$
代码
(体力、精灵球数为费用、精灵数为价值)$O(NMK)$

#include
using namespace std;
const int N=1010,M=510;
int n,V1,V2;
int f[N][M];
int main()
{
    cin>>V1>>V2>>n;
    for(int i=1;i<=n;i++)
    {
        int v1,v2;
        cin>>v1>>v2;
        for(int j=V1;j>=v1;j--)
            for(int k=V2-1;k>=v2;k--)//体力值不能为0所以不能从V2开始
                f[j][k]=max(f[j][k],f[j-v1][k-v2]+1);
    }
    cout<<f[V1][V2-1]<<" ";
    int k=V2-1;
    while(k>0&&f[V1][k-1]==f[V1][V2-1])k--;//先判断后操作
    cout<<V2-k<<endl;
    return 0;
}

数字组合

思路
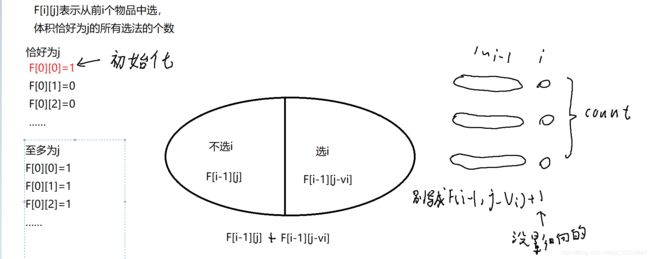
求方案数,并且恰好
$f[i][j]=f[i-1][j]+f[i-1][j-v_i]$不要写成
$f[i][j]=f[i-1][j]+f[i-1][j-v_i]+1$
初始化的时候记得$f[0][0]=1$其余为0
注意区分体积最多为j的初始化

代码

#include
using namespace std;

const int N=10010;

int n,m;
int f[N];
int main()
{
    cin>>n>>m;
    f[0]=1;//初始化为1，其他为0
    for(int i=0;i<n;i++)
    {
        int v;
        cin>>v;
        for(int j=m;j>=v;j--)
            f[j]+=f[j-v];
    }
    cout<<f[m];
    return 0;
}

买书

思路
费用恰好（要花完），完全背包求方案数，和数字组合很小
代码

#include
using namespace std;

const int N=1e3+10;
int f[N];
int a[N]={10,20,50,100};
int n;
int main()
{
    cin>>n;
    f[0]=1;//注意初始化
    for(int i=0;i<4;i++)
    {
        for(int j=a[i];j<=n;j++)
            f[j]+=f[j-a[i]];
    }
    cout<<f[n];
}

货币系统1021

思路
记得开long long
代码

#include
using namespace std;
const int N=3e3+10;
typedef long long ll;
int n,m,k;
ll v,f[N];
int main()
{
    cin>>n>>m;
    f[0]=1;
    for(int i=1;i<=n;i++)
    {
       cin>>v;
       for(int j=v;j<=m;j++)
            f[j]+=f[j-v];
    }
    cout<<f[m];
    return 0;
}

货币系统531

思路
根据题意，若两套货币系统相等，能表示的集合要相同，不能表示的集合也要相同。
可以得出：最优解一定从原序列中选出来，问题可以转化为某个面值是否必选。（最优性–>可行性问题–>可行性–>方案数）
那么，如何判断某一面值是否必选，可以转化为排序后，前1~i-1个面值凑成a[i]的方案数，若方案数为0，则a[i]必选，否则a[i]可以被前面的替换掉不必选。
模型转化为完全背包求方案数。
代码

#include
using namespace std;
const int N=110,M=25010;
int n;
int f[M],a[N];
int main()
{
    int T;
    cin>>T;
    while(T--)
    {
        cin>>n;
        for(int i=0;i<n;i++)cin>>a[i];
        sort(a,a+n);
        
        int m=a[n-1];
        memset(f,0,sizeof f);
        f[0]=1;
        
        int res=0;
        for(int i=0;i<n;i++)
        {
            if(!f[a[i]])res++;
            for(int j=a[i];j<=m;j++)
                f[j]+=f[j-a[i]];
        }
        cout<<res<<endl;
    }
    return 0;
}

多重背包问题 III

思路
比较好的题解
看数据模拟
滑动窗口图解

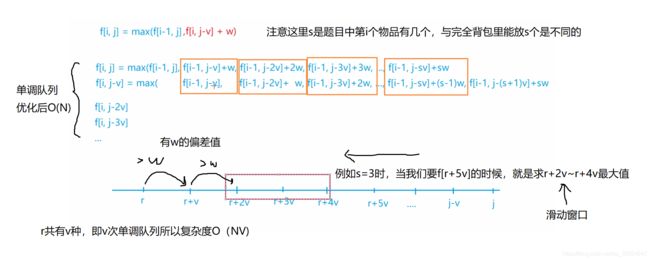
如何处理w的差值

摘自上面的博客里

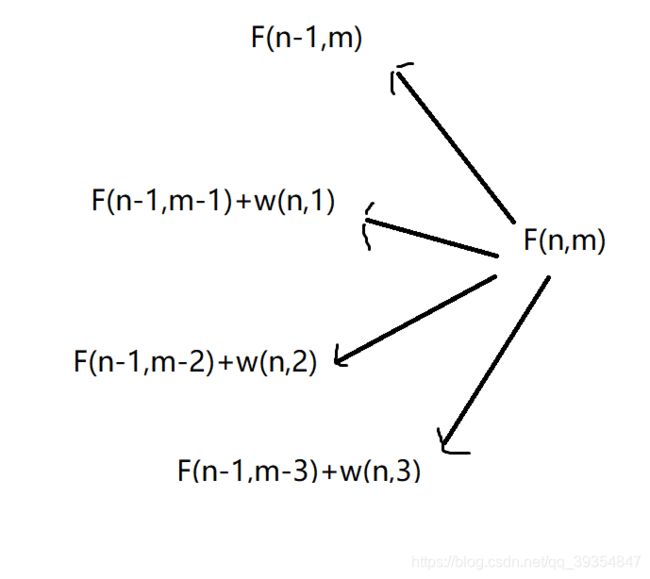
所以，我们可以得到
dp[j]    =     dp[j]
dp[j+v]  = max(dp[j] +  w,  dp[j+v])
dp[j+2v] = max(dp[j] + 2w,  dp[j+v] +  w, dp[j+2v])
dp[j+3v] = max(dp[j] + 3w,  dp[j+v] + 2w, dp[j+2v] + w, dp[j+3v])
...
但是，这个队列中前面的数，每次都会增加一个 w ，所以我们需要做一些转换
dp[j]    =     dp[j]
dp[j+v]  = max(dp[j], dp[j+v] - w) + w
dp[j+2v] = max(dp[j], dp[j+v] - w, dp[j+2v] - 2w) + 2w
dp[j+3v] = max(dp[j], dp[j+v] - w, dp[j+2v] - 2w, dp[j+3v] - 3w) + 3w
...
这样，每次入队的值是 dp[j+k*v] - k*w
代码转化
放到下面代码里就是dp[k]-(k-j)/v*w

滑动窗口模板（以滑动窗口中min为例子）

 hh = 0; tt = -1;// 初始化
 for (int i = 0; i < n; ++ i)//遍历数轴
 {
     if (i - k + 1 > q[hh]) ++ hh;//如果第i项加进去超过窗口宽度，队首出队
     while (hh <= tt && a[i] <= a[q[tt]]) -- tt;//保持a[i]>a[q[tt]],单调递增
     q[++ tt] = i;
     if (i + 1 >= k) printf("%d ", a[q[hh]]);//队头即最小值
 }

代码

#include
using namespace std;

const int N=2e4+10;
int n,m;
int f[N],g[N],q[N];
//f存储的是第i层,g存储第i-1层,q存储的是f,g数组中的下标(体积,例如:q[5]=r+3v);
//g[k]=f[i-1][k]
int main()
{
    cin>>n>>m;
    for(int i=0;i<n;i++)
    {
        int v,w,s;
        cin>>v>>w>>s;
        memcpy(g,f,sizeof f);//复制上一层结果
        for(int j=0;j<v;j++)//枚举余数
        {
            int hh=0,tt=-1;
            for(int k=j;k<=m;k+=v)//枚举体积（即数轴坐标）
            {
                if(hh<=tt&&q[hh]<k-s*v)hh++;//看有没有超过s件（窗口长度太长）
                if(hh<=tt)f[k]=max(f[k],g[q[hh]]+(k-q[hh])/v*w);
                //每次窗口max就是队头坐标转化后g[q[hh]]+(k-q[hh])/v*w
                while(hh<=tt&&g[q[tt]]-(q[tt]-j)/v*w<=g[k]-(k-j)/v*w)tt--;
                //(k-q[hh])/v和(k-j)/v就是下标
                q[++tt]=k;
            }
        }
    }
    cout<<f[m]<<endl;
    return 0;
}

庆功会

思路
裸的多重背包
代码

#include
using namespace std;
const int N=6010;
int n,m;
int f[N];
int main()
{
    cin>>n>>m;
    for(int i=0;i<n;i++)
    {
        int v,w,s;
        cin>>v>>w>>s;
        for(int j=m;j>=0;j--)
            for(int k=0;k<=s&&k*v<=j;k++)//注意这个
                f[j]=max(f[j],f[j-k*v]+k*w);
    }
    cout<<f[m];
    return 0;
}

混合背包问题

思路
只要看第i个物品时啥类型背包就行了
代码

#include
using namespace std;
typedef long long ll;
const int N=1e3+10;
int f[N];
int n,m;
int main()
{
    cin>>n>>m;
    for(int i=0;i<n;i++)
    {
        int v,w,s;
        cin>>v>>w>>s;
        if(s==0)//完全背包
        for(int j=v;j<=m;j++)
            f[j]=max(f[j],f[j-v]+w);
        else
        {
            if(s==-1)s=1;//01合并到多重里
            for(int k=1;k<=s;k*=2)//多重背包二进制
            {
                for(int j=m;j>=k*v;j--)
                    f[j]=max(f[j],f[j-k*v]+k*w);
                s-=k;
            }
            if(s)//剩下没打包的
            {
                for(int j=m;j>=s*v;j--)
                    f[j]=max(f[j],f[j-s*v]+s*w);
            }
        }
    }
    cout<<f[m]<<endl;
    
    return 0;
}

二维费用的背包问题

思路

代码

#include
using namespace std;
int n,V1,V2,v1,v2,w;
const int N=1e3+10;
int f[N][N];
int main()
{
    cin>>n>>V1>>V2;
    for(int i=1;i<=n;i++)
    {
        cin>>v1>>v2>>w;
        for(int j=V1;j>=v1;j--)
            for(int k=V2;k>=v2;k--)
                f[j][k]=max(f[j][k],f[j-v1][k-v2]+w);
    }
    cout<<f[V1][V2];
    return 0;
}

潜水员

思路
推荐：背包初始化

代码

#include
using namespace std;

const int N=22,M=80;

int n,m,k;
int f[N][M];

int main()
{
    cin>>n>>m>>k;
    memset(f,0x3f,sizeof f);//初始化为INF，只有合法地转移，
    f[0][0]=0;
    while(k--)
    {
        int v1,v2,w;
        cin>>v1>>v2>>w;
        for(int j=n;j>=0;j--)//>=0，负数是合法的，因为至少
            for(int k=m;k>=0;k--)
                f[j][k]=min(f[j][k],f[max(0,j-v1)][max(0,k-v2)]+w);
       /*
       for(int j=n;j>=v1;j--)//这样不能让负数也转移
            for(int k=m;k>=v2;k--)
                f[j][k]=min(f[j][k],f[j-v1][k-v2]+w);//max(0,j-v1)不是说到0就可以了，只是因为负数至少等效于取0，仍旧要转移的
       */
               
    }
    cout<<f[n][m]<<endl;
    return 0;
}

机器分配

思路
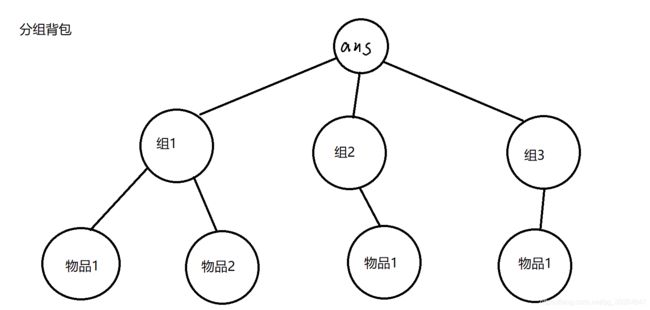
把公司当作物品组，机器数当作体积，价值为所给矩阵，转化为分组背包问题（同一个物品组只能选一个物品或者不选）

代码

#include
using namespace std;

int w[20][20],f[20][20],way[20];
int n,m;

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            cin>>w[i][j];
    
    for(int i=1;i<=n;i++)
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i-1][j];//第i组一个都不选
            for(int k=1;k<=j;k++)
                f[i][j]=max(f[i][j],f[i-1][j-k]+w[i][k]);
        }
    cout<<f[n][m]<<endl;
    int j=m;
    for(int i=n;i;i--)
        for(int k=0;k<=j;k++)
            if(f[i][j]==f[i-1][j-k]+w[i][k])
            {
                way[i]=k;
                j-=k;
                break;//找到直接跳出就行了
            }
    for(int i=1;i<=n;i++)cout<<i<<" "<<way[i]<<endl;
    return 0;
}

开心的金明

思路
裸的01
代码

#include
using namespace std;
const int N=3e4+10;
int n,m,k;
int v,w,dp[N];
int main()
{
    cin>>m>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>v>>w;
        w*=v;
        for(int j=m;j>=v;j--)
            dp[j]=max(dp[j],dp[j-v]+w);
    }
    cout<<dp[m];
    return 0;
}

有依赖的背包问题

思路
树形DP，把每个子树作为物品组，以体积来划分

啊这里对于树中的每个节点来说，就是一个分组背包问题。每个子节点是一组物品，
每个子节点的不同体积和每个体积所对应的最大价值，就是这个物品组中的物品。

图解版的题解


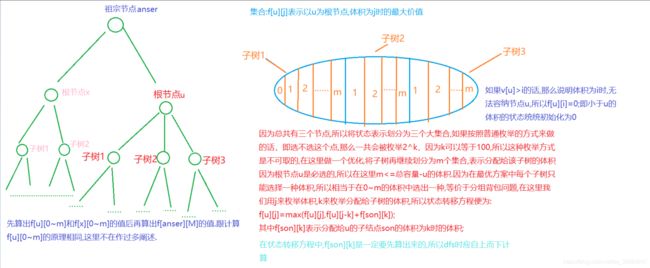
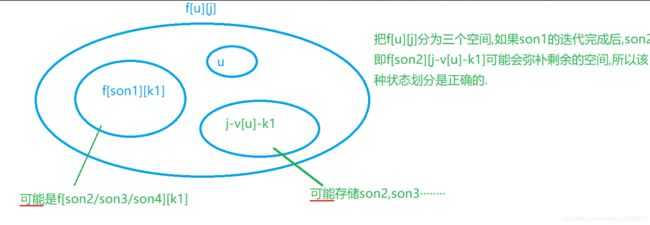
只是把分组背包的组换成根节点，物品换成子树。区别是第三重循环决策不再按选哪个物品（时间复杂度太高）而是分配个每个子树的体积

代码

#include
using namespace std;

const int N=110;
int n,m;
int h[N],e[N],ne[N],idx;
int v[N],w[N];
int f[N][N];

void add(int a,int b)//邻接表
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

void dfs(int u)
{
    for(int i=h[u];~i;i=ne[i])//循环物品组
    {
        int son=e[i];
        dfs(e[i]);
        
        //分组背包
        //这个时候当前结点我们看成是分组背包中的一个组，子节点的每一种选择我们都看作是组内一种物品
        for(int j=m-v[u];j>=0;j--)//循环体积，注意m-v[u]默认选根节点
            for(int k=0;k<=j;k++)//循环决策，给子节点son分配多少体积
                f[u][j]=max(f[u][j],f[u][j-k]+f[son][k]);
    }
    //把物品u加进去
    for(int i=m;i>=v[u];i--)f[u][i]=f[u][i-v[u]]+w[u];//别忘记默认选根节点
    for(int i=0;i<v[u];i++)f[u][i]=0;//如果根节点都装不下
}
int main()
{
    cin>>n>>m;
    memset(h,-1,sizeof h);//初始化
    int root;
    for(int i=1;i<=n;i++)
    {
        int p;
        cin>>v[i]>>w[i]>>p;
        if(p==-1)root=i;//根
        else add(p,i);
    }
    dfs(root);
    
    cout<<f[root][m]<<endl;
    return 0;
}

背包问题求方案数

思路
可以想成求最短路条数
法一：
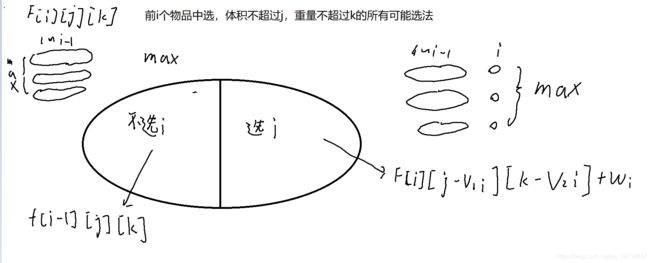
定义$f[i][j]$为从前i个物品中选，体积恰好为j的选法集合
$f[i][j]=max(f[i-1]j],f[i-1][j-v]+w)$

开一个$g[i][j]$存$f[i][j]$取到最优解方案数
不选第i个大$g[i][j]=g[i-1][j]$
选第i个大$g[i][j]=g[i-1][j-v]$
选不选第i个一样大$g[i][j]=g[i-1][j]+g[i-1][j-v]$
因为体积是恰好，所以要遍历一遍，求最大值（f[m]不是最大值）
然后再遍历一遍看看有没有相等的再求和
注意初始化

法二：
滑稽大佬的题解

关注两种方法的初始化问题

代码
法一

#include
using namespace std;
typedef long long ll;
int n,m;
const int N=1e3+10,mod=1e9+7;
ll f[N],g[N];
int main()
{
    cin>>n>>m;
    memset(f,-0x3f,sizeof f);//不能使体积恰好为j的不能被递推
    f[0]=0,g[0]=1;//显然选体积为0价值为0，而什么都不选的选法为1
    for(int i=0;i<n;i++)
    {
        int v,w;
        cin>>v>>w;
        for(int j=m;j>=v;j--)
        {
            if(f[j]<f[j-v]+w)
            {
                f[j]=f[j-v]+w;
                g[j]=g[j-v]%mod;
            }
            else if(f[j]==f[j-v]+w)
            {
                g[j]=(g[j]+g[j-v])%mod;
            }
        }
    }
    ll res=0,cnt=0;
    for(int i=0;i<=m;i++)res=max(res,f[i]);
    for(int i=0;i<=m;i++)
        if(res==f[i])cnt=(cnt+g[i])%mod;
    cout<<cnt;
    return 0;
}

法二代码（滑稽大佬的）

#include
#include

using namespace std;

const int N=1010,mod=1e9+7;

int f[N],g[N];

int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=0;i<=m;i++) g[i]=1;//初始化时我们易知，不论是哪个体积下，总有一个对应的最大价值，方案数为1

    for(int i=1;i<=n;i++)
    {
        int v,w;
        cin>>v>>w;
        for(int j=m;j>=v;j--)
        {
            if(f[j]<f[j-v]+w)
            {
                g[j]=g[j-v]; //当f[j]
                f[j]=f[j-v]+w;
            }
            else if(f[j]==f[j-v]+w) g[j]=(g[j]+g[j-v])%mod;//若相等，说明存在了2个节点，他们路径都符合条件
            //可以递推到g[j]
        }
    }

    cout<< g[m] <<endl;//最后输出这个体积不超过m对应最大价值的方案数即可！
    return 0;
}

背包问题求具体方案

思路
推荐题解参考
求获得最大价值的具体方案，并令字典序最小
求具体方案：判断出每个每个物品是否被选
首先不能进行状态压缩
记录方案，从哪个路径走到$f[n][m]$
怎么判断？
如果$f[n][m]=f[n-1][m]那么从不选第n个转移过来如果$f[n][m]=f[n-1][m-v[n]]+w[n]$那么从选第n个转移过来
也可能两个都可以，即第n个物品可选可不选

字典序最小：贪心
从第一个开始，每个物品有选有三种情况
只能选–>一定选
只能不选–>一定不选
可选可不选–>一定选

但是我们一般dp的时候是倒着推具体方案的，我们要最小字典序是要从前往后推如何解决呢？那么在输入之后，dp的时候从后往前推即可。

另外一种思路是开一个数组记录选哪个
代码

#include
using namespace std;
const int N=1e3+10;
int f[N][N],v[N],w[N];
int n,m;
int main()
{   
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    for(int i=n;i>=1;i--)
    {
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i+1][j];//从后往前别写错
            if(j>=v[i])f[i][j]=max(f[i][j],f[i+1][j-v[i]]+w[i]);
        }
    }
    //f[1][m]是最大值
    int j=m;
    for(int i=1;i<=n;i++)
    {
        if(j>=v[i]&&f[i][j]==f[i+1][j-v[i]]+w[i])//能选就一定要选   
        {
            cout<<i<<" ";
            j-=v[i];
        }
    }
    return 0;
}

能量石

思路
讲的比较好的博客
暴力解法：把把所有全排列整出来然后每个排列做01背包取最值
这里有个问题：为啥不能直接01背包？
对于一般的选物品，无论物品如何排列，我们都可以得到相同的答案。但是本题的特殊点在于，不同顺序选的话，物品的价值是变的，前面选的物品时间越长，后面物品价值越小（甚至为0），这样DP具有后效性，没法整，出来的只是局部最优解。
这时候我们可以利用贪心缩小决策范围，将最优解的排序确定，然后进行01
贪心:
其中$S_i$表示前i个时间之和（前缀）
$S_i=t_1+t_2+\dots \dots +t_i$
$E_1-L_1+E_2-L_2\ast S_1+\dots \dots +E_n-L_n\ast S_{n-1}$
第i项和第i+1邻项交换

状态	公式
交换前	$E_i-L_i\ast S_{i-1}+E_{i+1}-L_{i+1}\ast S_i$
交换后	$E_{i+1}-L_{i+1}\ast S_{i-1}+E_i-L_i\ast (S_i-t_i+t_{i+1})$
比较	$\frac{L_i}{t_i}?\frac{L_{i+1}}{t_{i+1}}$

排序后产生另外一个问题：为啥不直接拿完最优解排序。
因为你拿一块能量石后未必会增加总能量，反而可能因为拿了这块后造成后面的能量损失过多，因此如果选择不拿的话是有可能减少这些损失的，反而有利。
DP状态转移方程
定义$f[i][j]$为从前i个物品中选，耗时恰好为j的所有选法集合的最大价值
$f[i][j]=max(f[i-1][j],f[i-1][j-s[i]]+max(0,e[i]-l[i]\ast (j-s)))$
代码

#include
using namespace std;

const int N=1e4+10;
int n;
struct Stone
{
    int s,e,l;
    bool operator<(const Stone &W)const
    {
        return s*W.l<l*W.s;
    }
}stone[N];
int f[N];
int main()
{
    int T;
    cin>>T;
    for(int C=1;C<=T;C++)
    {
        int m=0;
        cin>>n;
        for(int i=0;i<n;i++)
        {
            int s,e,l;
            cin>>s>>e>>l;
            stone[i]={s,e,l};
            m+=s;
        }
        sort(stone,stone+n);
        memset(f,-0x3f,sizeof f);
        f[0]=0;
        for(int i=0;i<n;i++)
        {
            int s=stone[i].s,e=stone[i].e,l=stone[i].l;
            for(int j=m;j>=s;j--)
                f[j]=max(f[j],f[j-s]+e-(j-s)*l);
        }
        int res=0;
        for(int i=0;i<=m;i++)res=max(res,f[i]);
        printf("Case #%d: %d\n",C,res);
    }
    return 0;
}

金明的预算方案

思路
有依赖的分组背包问题
模型的转化
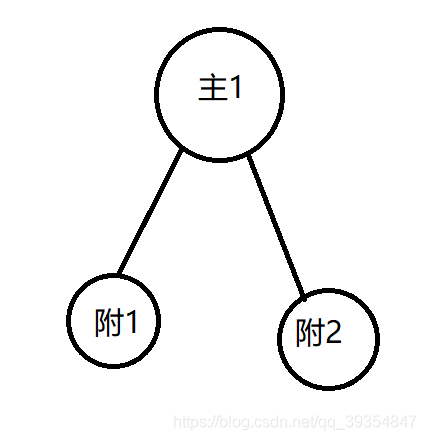
分组背包：每个主件的附件决策选法其实就是一个物品，他们是互斥的

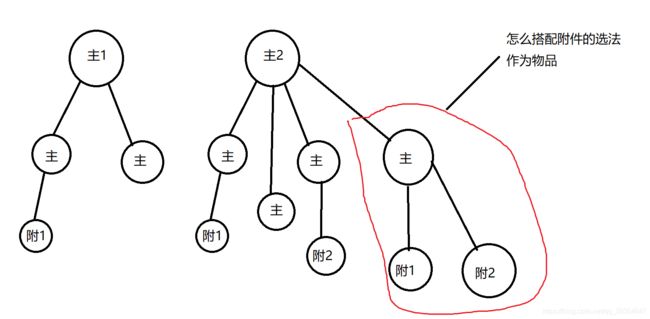
关系的输入与存储

如何用代码实现上述这种一个连着多个而且只有一层关系的结构（附件不会成为附件的附件）
用vector数组即可，同时它仅有两种属性，那么可以用pair类型的vector存储这种依赖关系，如果是根，则存PII类型的master数组中，如果不是则存servent的vector数组。如果有多个属性的话把PII改成struct存储即可

PII master[N];
vector<PII>servent[N];

如何枚举每个选法：通过观察发现我们可以利用二进制来实现枚举例如第一张图的主2
默认初值选上主件，每个附件选或不选，二进制枚举附件选法
代码

#include
using namespace std;
#define v first
#define w second

typedef long long ll;
const int N=4e4+10;
typedef pair<int,int>PII;
ll n,m;
PII master[N];
vector<PII>servent[N];//附件
int f[N];
int main()
{
    cin>>m>>n;
    for(int i=1;i<=n;i++)
    {
        int v,w,q;
        cin>>v>>w>>q;
        if(!q)master[i]={v,v*w};
        else servent[q].push_back({v,v*w});
    }
    
    for(int i=1;i<=m;i++)
        if(master[i].v)
        {
            for(int j=m;j>=0;j--)
            {
                auto &sv=servent[i];
                for(int k=0;k<(1<<sv.size());k++)//二进制枚举附件选法
                {
                    int v=master[i].v,w=master[i].w;//默认选主件
                    for(int u=0;u<sv.size();u++)
                        if(k>>u&1)
                        {
                            v+=sv[u].v;
                            w+=sv[u].w;
                        }
                    if(j>=v)f[j]=max(f[j],f[j-v]+w);
                }
            }
        }
    cout<<f[m]<<endl;
    return 0;
}