数据结构——树基础
本人将树相关知识总结为初、中、高三篇,本文属于树结构的初篇,主要阐述几种经典的树形结构,主要总结树、二叉树、线索二叉树、森林等基础相关知识。
本篇内容包含:树,二叉树,平衡二叉树,二叉排序树,满二叉树,完全二叉树,线索二叉树,森林等基础部分进行总结,有基础的可以直接在目录中选择代码部分观看,关于哈夫曼树,线段,b树,红黑树,最小生成树等在基础部分不进行总结,后面会单独出。
中级篇在:二叉排序树/平衡二叉树/哈夫曼树(主要总结树二叉排序树/平衡二叉树/哈夫曼树等)
目录
1、树的逻辑结构
树的相关术语:
树的几种类型:
1、二叉树
2、满二叉树
3、完全二叉树
4、二叉排序树
5、平衡二叉树
二叉树的性质:
二叉树性质:
满二叉树性质:
完全二叉树性质
2、树的存储结构
树的顺序存储结构
顺序代码
树的链式存储结构
链式代码
3、二叉树遍历及创建
二叉树的遍历
先序遍历 DLR
先序遍历代码
中序遍历LDR
中序遍历代码
后序遍历LRD
后序遍历代码
层次遍历
层次遍历代码
二叉树创建
总结:二叉树遍历整体代码
二叉树相关算法
线索二叉树遍历
树、森林遍历
树、森林、二叉树转换
树和森林的遍历
森林的遍历
首先我们先进行回顾,数据结构第一章提到数据的逻辑结构有线性结构,和非线性结构,如下图:
在此之前已经将线性结构学完,接下来进行非线性结构的学习,首先就是树。
1、树的逻辑结构
树的定义:树:n (n≥0)个结点的有限集合。当n=0时,称为空树;任意一棵非空树满足以下条件:
1)有且仅有一个特定的称为根的结点;
2当n>1时,除根结点之外的其余结点被分成m(m>0)个互不相交的有限集合T, T,, ... ,Tm,其中每个集合又是一棵树,并称为这个根结点的子树。
树的应用:树,族谱,算法分析等,
树的相关术语:
如下图所示:所有节点都有来自双亲节点的度,除根节点,因此,根节点的定义为:根结点(root)是树的一个组成部分,也叫树根。所有非空的二叉树中,都有且仅有一个根结点。它是同一棵树中除本身外所有结点的祖先,没有父结点。
叶子结点:度为0的结点,也称为终端结点。
分支结点:度不为0的结点,也称为非终端结点。
结点的度:结点所拥有的子树的个数。
树的度:树中各结点度的最大值。
结点所在层数:根结点的层数为1;对其余任何结点,若呆结点在第k层,则其孩子结点在第k+1层。
树的深度:树中所有结点的最大层数,也称高度。
树的几种类型:
1、二叉树
二叉树是另一种树形结构,其特点是每个结点至多只有两棵子树(即二叉树中不存在度大于2的结点),并且二叉树的子树有左右之分,其次序不能任意颠倒。除根结点具有2个度外所有结点均只有0或1个度。
2、满二叉树
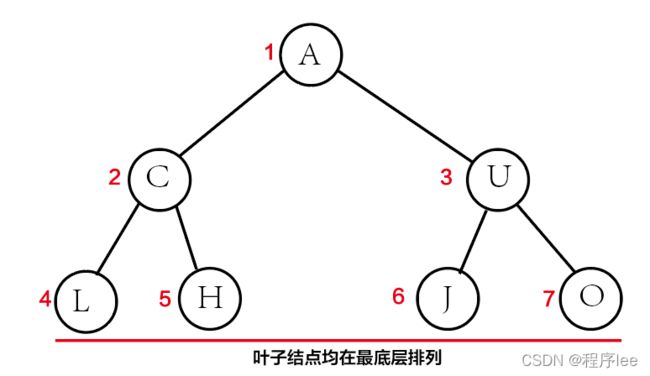
一棵高度为h,且含有2-1个结点的.二叉树称为满二叉树,即树中的每层都含有最多的结点,满二叉树的叶子结点都集中在二叉树的最下一层,并且除叶子结点之外的每个结点度数均为2。
3、完全二叉树
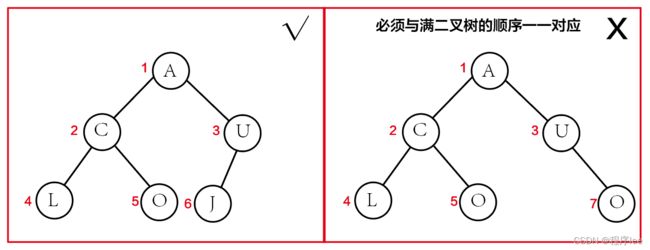
高度为h、有n个结点的二叉树,当且仅当其每个结点都与高度为h的满二叉树中编号为1~n的结点一一对应时,称为完全二叉树。
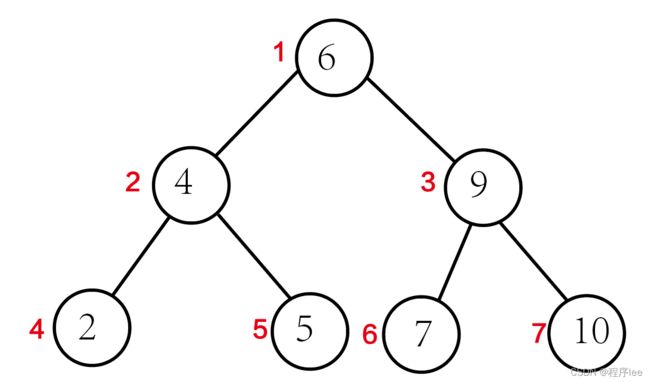
4、二叉排序树
(二叉搜索树、二叉查找树、BST)
若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
任意节点的左、右子树也分别为二叉查找树;
没有键值相等的节点。
5、平衡二叉树
平衡二叉搜索树(Self-balancing binary search tree)又被称为AVL树(有别于AVL算法),且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。
二叉树的性质:
二叉树性质:
1、非空二叉树上的叶子结点数等于度为2的结点数加1,即no=n2+l。
2、非空二叉树中,第n层的结点总数不超过2的n-1次方
3、非空二叉树中,深度为h总结点数最多不超过2的h次方-1
满二叉树性质:
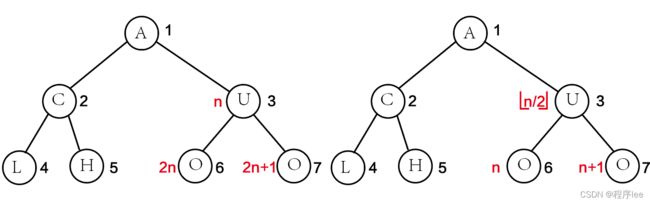
可以对满二叉树按层序编号约定编号从根结点(根结点编号为1)起,自上而下,自左向右。这样,每个结点对应一个编号,对于编号为i的结点,若有双亲,则其双亲为⌊2/n⌋,若有左孩子,则左孩子为2n;若有右孩子,则右孩子为2n+ 1。
每行总结点数为2的n-1次方
完全二叉树性质
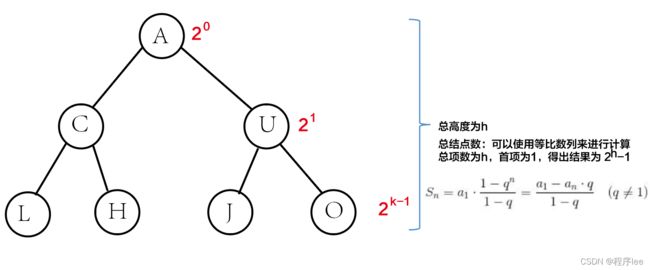
具有n个(n>0)结点的完全二叉树的高度为「log2(n+1)]或Llog2n]+1。
设高度为h,根据性质关系可以成立以下等式
2、树的存储结构
树的顺序存储结构
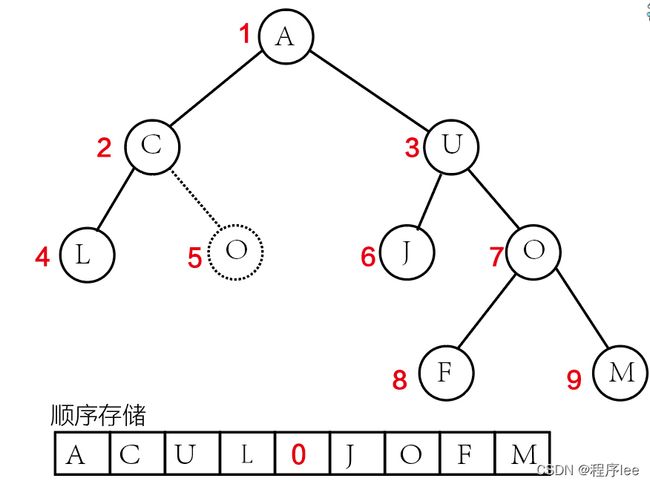
实现:按满二叉树的结点层次编号,依次存放二叉树中的数据元素。如下图所示
顺序代码
//二叉树的顺序存储
#define MAXSIZE 20
struct SqBiTree
{
Typedef TlemType SqBiTree[MAXSIZE]; //定义数组空间
SqBiTree bt; //定义一个变量记录数量
}这种方式在实际工作中很少会用到,对于删除,添加,寻找孩子,双亲等都不方便并且当分支节点为空过多时,浪费存储空间。更适合与满二叉树和完全二叉树。因此常常采用链式存储方式
树的链式存储结构
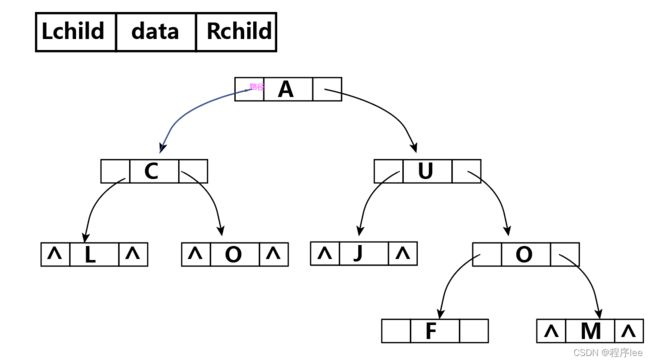
由于顺序存储的空间利用率较低,因此二叉树一般都采用链式存储结构,用链表结点来存储二叉树中的每个结点。在二叉树中,结点结构通常包括若干数据域和若干指针域,二叉链表至少包含3个域:数据域data、左指针域Lchild和右指针域Rchild
链式代码
#define _CRT_SECURE_NO_WARNINGS
typedef struct BiNode {
TelemType data; //数据域
struct BiNode* Lchild, * Rchild //建立左指针和右指针
}BiNode, * BiTree;3、二叉树遍历及创建
二叉树的遍历
我们需要先讲遍历方式,再介绍创建吗,因为二叉树的特性,无论是遍历还是创建等操作,都需要基于先序遍历或中序遍历或后序遍历才能进行,因此可以按照递归的思路进行遍历的运算。思路如下:按照遍历子树的原则常见的遍历顺序有如下几种:DLR,LDR,LRD.DRL,RDL,RLD. 通常考虑优先左子树的方式,因此还剩下如下三种方式即:DLR,LDR,LRD。暂时仅仅给出伪代码,包含层次遍历在后面会将整体遍历代码贴出来,对于非遍历方法暂不讲解。
先序遍历 DLR
先序遍历(PreOrder)的操作过程如下。若二叉树为空,则什么也不做;否则1、访问根结点;
2、先序遍历左子树 3、先序遍历右子树,对应的递归算法如下:
先序遍历代码
void PreOrder(BiTree t) { //先序遍历函数
if(t==NULL) {
return false; //树为空
}
visit(t); //遍历根结点
PreOrder(t->Lchild); //遍历左子树
PreOrder(t->Rchild) //遍历右子树
}中序遍历LDR
中序遍历(InOrder的操作过程如下。若二叉树为空,则什么也不做否则1、中序遍历左子树;
2、访问根结点3、中序遍历右子树。如图所示A左面数值即为根结点的左面,遍历后A右面的数值即在根结点右面
中序遍历代码
void InOrder(BiTree t) { //先序遍历函数
if(t==NULL) {
return false; //树为空
}
InOrder(t->Lchild); //遍历左子树
visit(t); //遍历根结点
InOrder(t->Rchild) //遍历右子树
}后序遍历
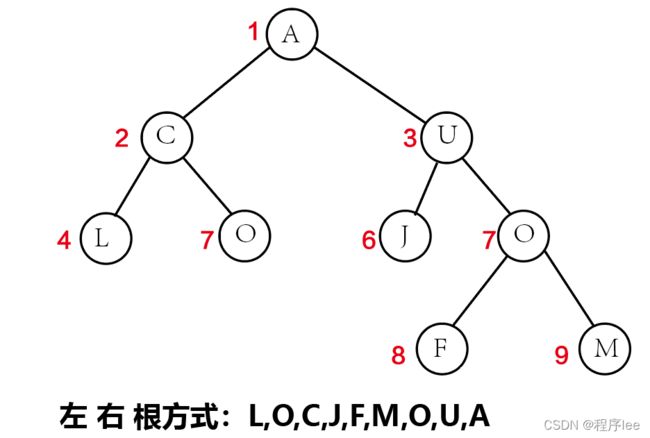
后序遍历(PostOrder)的操作过程如下。若二叉树为空,则什么也不做否则1、后序遍历左子树;
2、后序遍历右子树 3、访问根结点。
后序遍历代码
void PostOrder(BiTree t) { //先序遍历函数
if(t==NULL) {
return false; //树为空
}
PostOrder(t->Lchild); //遍历左子树
PostOrder(t->Rchild) //遍历右子树
visit(t); //遍历根结点
}层次遍历
层次遍历借助于队列的思想,①首先将根结点放入队列中 ②判断队列是否空 ③头结点出队④访问出队节点⑤判断左右子树是否为空,根结点入队。
层次遍历代码
#define MAX_SIZE 20
typedef struct BiTree { //二叉链表
int data;
struct BiTree* Rchild, * Lchild;
}BiTree;
typedef struct Quene { //循环队列
BiTree* data[MAX_SIZE];
int front, rear; //定义头尾指针
}Quene;
void LevalOrder(BiTree* T) {
BiTree* p; Quene* q; //定义指针
InitQuene(q); //初始化队列
enQuene(q,p); //根结点入队
while (!QueneEmpty(q)) //队列为空则退出循环
//(此处是要判断子树是否还有孩子)
{
deQuene(q,p); //出队
printf("%d",p->data); //访问节点
if (p->Lchild) { enQuene(q, p->Lchild); } //左孩子入队
if (p->Rchild) { enQuene(q, p->Rchild); } //右孩子入队
}
}二叉树创建
假设按照先序序列输入:A C L O U J O F M
由此可看出,在仅仅给出先序序列情况下,并不能确定唯一的树形结构,只有在确定中序和先序的情况下才能确定唯一的树形结构,那么我们可以在输入时进行一些改变。
假设按照先序序列输入:A C L O U # J O F M 将空位以 # 代替,这样便可以确定唯一的树形结构了。
这里理解了,就可以手撸代码了,代码如下,注意这里的两种创建方式
返回值创建(推荐)
TNode CreatBinaryTree(TNode T){
char ch;
printf("请输入当前结点的值");
scanf("%c",&ch);
getchar();
if (ch=='#') {
T = NULL; //节点为空
}
else {
if (T = (TNode)malloc(sizeof(BiTree))) { //开辟空间并检测是否成功
T->data = ch;
T->Lchild = CreatBinaryTree(T->Lchild);
T->Rchild = CreatBinaryTree(T->Rchild);
//CreatBinaryTree(T->Lchild); //构造左子树
//CreatBinaryTree(T->Rchild); //构造右子树
}
}注意这里一定要接收递归的返回值,如果不接收,这里并不能对递归外的参数进行更改。
引用/双指针创建
void CreatBinaryTree(TNode &T){
char ch;
printf("请输入当前结点的值");
scanf("%c",&ch);
getchar();
if (ch=='#') {
T = NULL; //节点为空
}
else {
if (T = (TNode)malloc(sizeof(BiTree))) { //开辟空间并检测是否成功
T->data = ch;
/* T->Lchild = CreatBinaryTree(T->Lchild);
T->Rchild = CreatBinaryTree(T->Rchild);*/
CreatBinaryTree(T->Lchild); //构造左子树
CreatBinaryTree(T->Rchild); //构造右子树
}
}
}这里还是建议用返回值的方式便于理解
总结:二叉树遍历整体代码
#define _CRT_SECURE_NO_WARNINGS
#include
#include
//二叉树先序遍历
typedef struct BiTree { //链式建立
char data;
struct BiTree* Lchild;
struct BiTree* Rchild; //左右孩子指针
}BiTree,*TNode;
TNode CreatBinaryTree(TNode T){ //创建
char ch;
printf("请输入当前结点的值");
scanf("%c",&ch);
getchar();
if (ch=='#') {
T = NULL; //节点为空
}
else {
if (T = (TNode)malloc(sizeof(BiTree))) { //开辟空间并检测是否成功
T->data = ch;
T->Lchild = CreatBinaryTree(T->Lchild);
T->Rchild =CreatBinaryTree(T->Rchild)
}
}
return T;
}
void PreOrderTraverse(TNode T)//二叉树的先序遍历
{
if (T == NULL)
return;
printf("%c ", T->data);
PreOrderTraverse(T->Lchild);
PreOrderTraverse(T->Rchild);
}
void InOrderTraverse(TNode T)//二叉树的中序遍历
{
if (T == NULL)
return;
InOrderTraverse(T->Lchild);
printf("%c ", T->data);
InOrderTraverse(T->Rchild);
}
void PostOrderTraverse(TNode T)//二叉树的后序遍历
{
if (T == NULL)
return;
PostOrderTraverse(T->Lchild);
PostOrderTraverse(T->Rchild);
printf("%c ", T->data);
}
int main() {
TNode T= (TNode)malloc(sizeof(BiTree));
printf("请输入构建二叉树的序列");
T=CreatBinaryTree(T);//构建二叉树
PreOrderTraverse(T);//先序输出
InOrderTraverse(T);//中序输出
PostOrderTraverse(T);//后序输出
return 0;
}
二叉树相关算法
二叉树深度计算
int Depth(BiTree T){
if (T == NULL) return 0;
else
{
m = Depth(T.Lchild);
n = Depth(T.Rchild);
if (m > n) return (m + 1);
else{
return (n + 1);
}
}
}二叉树结点计算
int NodeCount(BiTree T) {
if (T==NULL) {
return 0;
}
else {
return NodeCount(T->Lchild) +
NodeCount(T->Rchild) + 1;
}
}线索二叉树遍历
当需要找树的前驱后继结点时,仅仅依靠左右孩子指针是完全不够的,左右指针只可以找到孩子结点无法找到双亲,因此我们引出了线索二叉树的概念
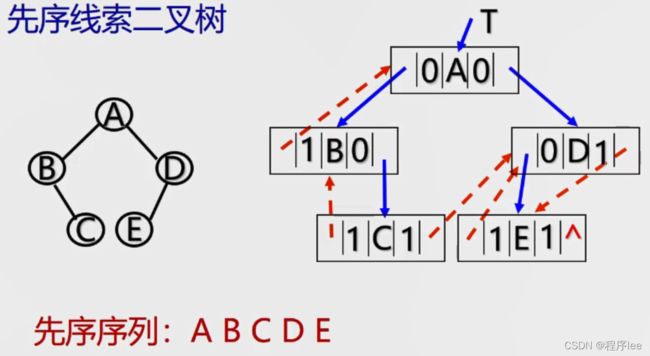
如果某个结点的左孩子为空,则将空的左孩子指针域改为指向其前驱;如果某结点的右孩子为空,则将空的右孩子指针域改为指向其后继,因此我们增加两个指针域,ltag和rtag。实际上是标记域
ltag = 0lchild指向该结点的左孩子
ltag = 1lchild指向该结点的前驱
rtag = 0 rchild指向该结点的右孩子
rtag = 1 rchild指向该结点的后继
typedef struct BiTree { //链式建立
char data;
int ltag, rtag; //标记域
struct BiTree* Lchild;
struct BiTree* Rchild; //左右孩子指针
}BiTree, * TNode;图片来自于 bilibili 王卓老师
树、森林遍历
之前有对树进行介绍,因此这里将树和森林进行对比:
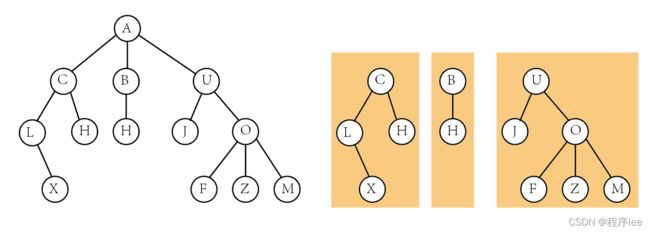
森林就是m颗不想交的树的集合,简单思考就是把树的根结点去掉就是森林。
树的存储表示法:
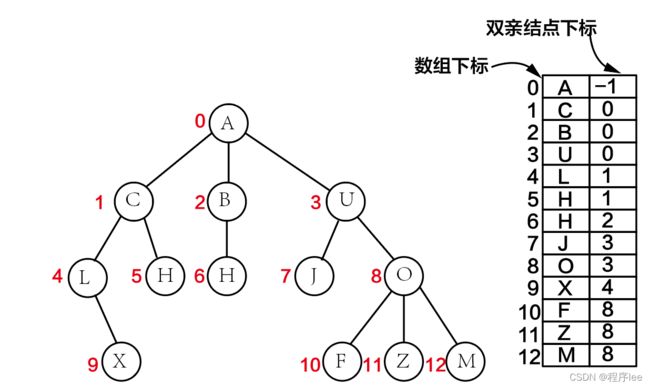
双亲表示法:这种存储方式采用一组连续空间来存储每个结点,同时在每个结点中增设一个伪指针,指示其双亲结点在数组中的位置。
孩子表示法:是将每个结点的孩子结点都用单链表链接起来形成一个线性结构,此时n个结点就有n个孩子链表(叶子结点的孩子链表为空表)
这种存储方式寻找子女的操作非常直接,而寻找双亲的操作需要遍历n个结点中孩子链表指针域所指向的n个孩子链表。
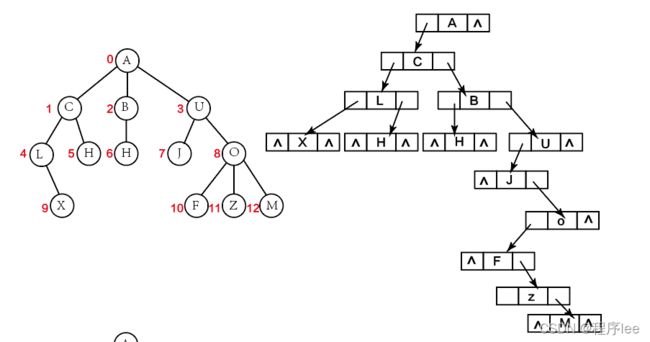
孩子兄弟表示法又称二叉树表示法,即以二叉链表作为树的存储结构。孩子兄弟表示法使每个结点包括三部分内容:结点值、左指向结点第一个孩子结点的指针,及右指向结点下一个兄弟结点的指针(沿此域可以找到结点的所有兄弟结点)
树、森林、二叉树转换
树转二叉树:
给定一个树就能够找到与之对应的二叉树,因为二者都可以用二叉链表形式表示。
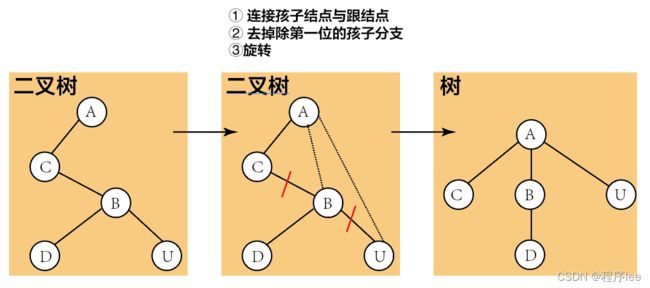
二叉树转树:
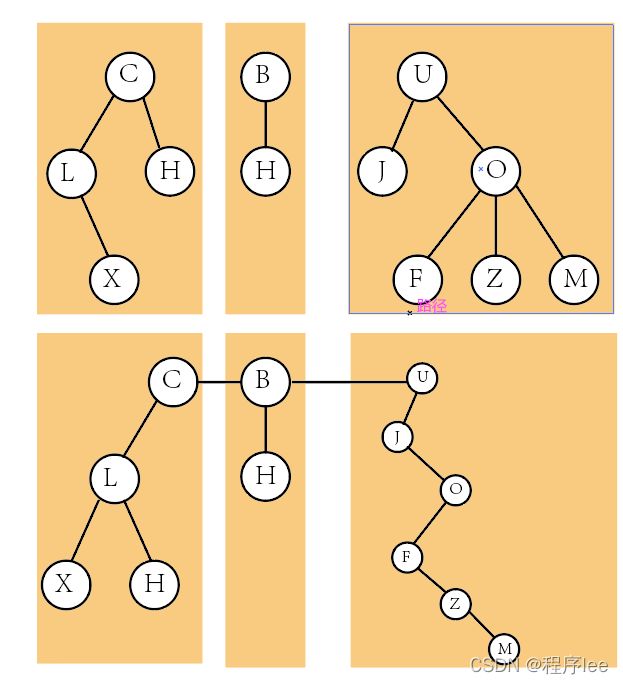
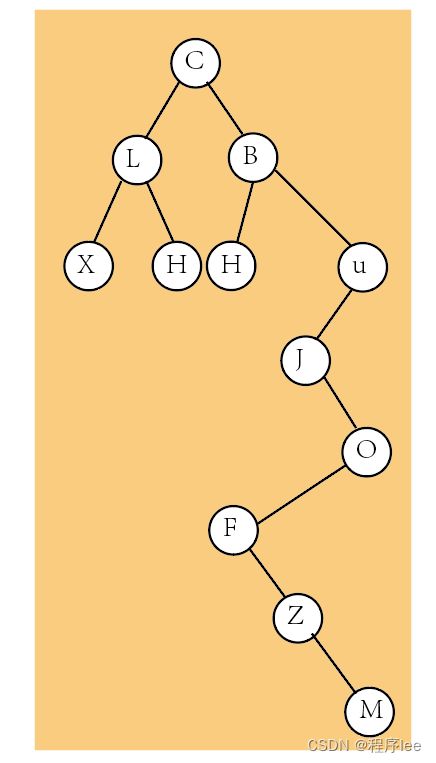
森林转换成二叉树:
步骤①分别将各树转换成二叉树:② 将根相连 ③旋转
二叉树转换成森林:
根据上图将根与最右侧所有线断开,再旋转,再把二叉树转换成树即可。这里不做演示了。
树和森林的遍历
树的遍历
若树不空,则先访问根结点,然后依次先根遍历各棵子树。先根遍历
若树不空,则先依次后根遍历各棵子树,然后访问根结点。后根遍历
若树不空,则自上而下自左至右访问树中每个结点。层次遍历
这里的遍历方式和二叉树基本相同就不过多赘述,这里没有中序遍历是因为树和二叉树不同除左右两结点外,中间有很多结点,主要来研究森林的遍历
森林的遍历
将森林看作由三部分构成: 本质上也是递归的过程,这里也可以进行根的先中后遍历方式
1、森林中第一棵树的根结点;
2.森林中第一棵树的子树森林;
3.森林中其它树构成的森林。
到这里基本对于树的基础部分就结束了,关于二叉搜索,哈夫曼树,红黑树等就不放在这里概括了,本文是本人集合了王道考研,b站懒猫老师,王卓老师的课程进行的归纳总结,如有遗漏欢迎大家指正,谢谢