Leetcode刷题——数组

数组定义

一、二分查找：

1.二分查找使用条件

1.数组为有序数组（无序数组可以sort变为有序数组）
2.数组中无重复元素

注意事项：
区间定义要遵循不变量的原则，区间定义有左闭右闭[left,right]或者左闭右开[left，right)

2.二分法写法

我习惯使用左闭右闭的写法

定义target在左闭右闭的区间里即[left,right],

• whiile(left<=right),因为left可以等于right,即left==right

三、Leetcode题目：

1.二分查找

二分查找力扣链接

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left=0;
        int right=nums.size()-1;
        while(left<=right)
        {
            int mid=left+(right-left)/2;
            if(nums[mid]>target)
            {
                right=mid-1;
            }
            else if(nums[mid]<target)
            {
                left=mid+1;
            }
            else
            {
                return mid;
            }
        }
        return -1;
    }
};

2.搜素插入位置

搜索插入位置题目链接
这道题只需要在二分查找基础上添加几行代码，在数组中没有target情况下怎么求插入的target索引，
第一种方法暴力求解：遍历数组，如果遇到nums[i]大于target时直接返回i，i就是我们要插入的位置。
时间复杂度O(N).
注：i，nums.size()可以理解为闭区间[0,nums.size()-1].

  //暴力解法
        for(int i=0;i<nums.size();i++)
        {
            if(nums[i]>target)
            {
                return i;
            }
        }
        return  nums.size();

第二种方法二分查找：直接返回right+1;
考虑四种情况：
1.target在数组起始位置之前
2.target插入数组中间位置
3.target等于数组中某个元素
4.target在数组末尾位置之后
时间复杂度为O(log(N))

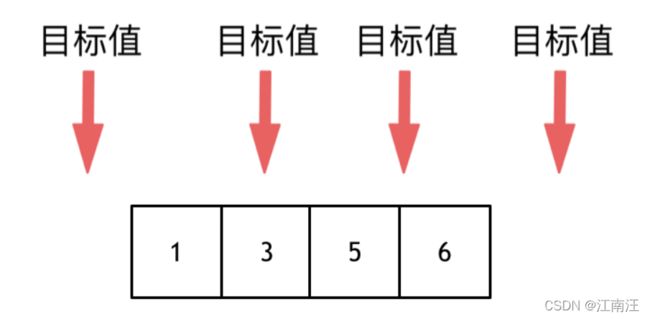
 // 分别处理如下四种情况
        // 目标值在数组所有元素之前  [0, -1]
        // 目标值等于数组中某一个元素  return middle;
        // 目标值插入数组中的位置 [left, right]，return  right + 1
        // 目标值在数组所有元素之后的情况 [left, right]， return right + 1
        return right + 1;

整体代码：

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int left=0;
        int right=nums.size()-1;
        while(left<=right)
        {
            int mid=left+(right-left)/2;
            if(nums[mid]>target)
            {
                right=mid-1;
            }
            else if(nums[mid]<target)
            {
                left=mid+1;
            }
            else
            {
                return mid;
            }
        }
        //暴力解法
        for(int i=0;i<nums.size();i++)
        {
            if(nums[i]>target)
            {
                return i;
            }
        }
        return  nums.size();
        //二分查找
        return right+1;
    }
};

3.在排序数组中查找元素的第一个和最后一个位置

二分查找使用大多数场景都是数组为有序数组且数组中无重复元素，那么如果有重复元素使用二分查找可以吗，如果可以那么应该注意什么？
使用二分法找到target后，在有重复元素的情况下target位置的左边和右边的数组值都有可能是target，怎么将所有的target找到？
方法：用两次二分法找到target的左边界和右边界。
先求左边界：

 int getleftborder(vector<int>&nums,int target){
        int left=0;
        int right=nums.size()-1;
        int leftborder=-2;
        while(left<=right)
        {
            int mid=left+(right-left)/2;
            if(nums[mid]>target){
                right=mid-1;
            }
            else if(nums[mid]<target){
                left=mid+1;
            }
            else{
                right=mid-1;
               leftborder=right;
            }
        }
        return leftborder;
    }

leftborder=right,right一直在减，直到找到target的左边界，此时左边界是开区间的左边界，取不到。

再求右边界：

  int getrightborder(vector<int>&nums,int target){
        int left=0;
        int right=nums.size()-1;
        int rightborder=-2;
        while(left<=right)
        {
            int mid=left+(right-left)/2;
            if(nums[mid]>target){
                right=mid-1;
            }
            else if(nums[mid]<target){
                left=mid+1;
            }
            else{
                left=mid+1;
                rightborder=left;
            }
        }
        return rightborder;
    }

rightorder=left=mid+1,left一直在加，直到找到target的右边界，此时右边界同样是开区间的右边界，取不到。
如果数组有target，则返回 {leftborder+1,rightborder+1},没有target，则返回{-1，-1}。
整体代码：

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int leftborder=getleftborder(nums,target);
        int rightborder=getrightborder(nums,target);
        if(leftborder==-2||rightborder==-2){
            return {-1,-1};
        }
        else{
            return {leftborder+1,rightborder-1};
        }
        return {-1,-1};
    }
    int getrightborder(vector<int>&nums,int target){
        int left=0;
        int right=nums.size()-1;
        int rightborder=-2;
        while(left<=right)
        {
            int mid=left+(right-left)/2;
            if(nums[mid]>target){
                right=mid-1;
            }
            else if(nums[mid]<target){
                left=mid+1;
            }
            else{
                left=mid+1;
                rightborder=left;
            }
        }
        return rightborder;
    }
    int getleftborder(vector<int>&nums,int target){
        int left=0;
        int right=nums.size()-1;
        int leftborder=-2;
        while(left<=right)
        {
            int mid=left+(right-left)/2;
            if(nums[mid]>target){
                right=mid-1;
            }
            else if(nums[mid]<target){
                left=mid+1;
            }
            else{
                right=mid-1;
               leftborder=right;
            }
        }
        return leftborder;
    }
};

4.移除元素

27. 移除元素

暴力破解法

• 两次for循环：外层for循环用来寻找数组中等于val的值，内层循环用来在原数组上删除val
• 数组中有多个val时，数组的size在变化，外层i也在变化，i–和size–。

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int size=nums.size();
        for(int i=0;i<size;i++){
            if(nums[i]==val){
                for(int j=i+1;j<nums.size();j++){
                    nums[j-1]=nums[j];
                }
                i--;
                size--;
            }
        }
        return size;
    }
};

快慢指针法

• 注意怎么更新指针，如果nums[fast]=val,只更新fast++，这样slow和fast之间差一个“位置”，再覆盖
• 最后要返回slow。

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
       int slow=0;
       for(int fast=0;fast<nums.size();fast++){
           if(nums[fast]!=val)
           {
               nums[slow]=nums[fast];
               slow++;
           }
       }
       return slow;
    }
};