浙江大学数据结构练习笔记:链表,二叉树.二叉搜索树(更新中)
浙江大学数据结构练习笔记:链表,二叉树,二叉搜索树(更新中)
由于本人水平有限,整理的代码若有错漏欢迎指出
文章目录
- 浙江大学数据结构练习笔记:链表,二叉树,二叉搜索树(更新中)
-
- 线性结构:多项式加法(链表实现)
- 二叉树:
-
- 二叉树的储存:链表储存
- 二叉树的遍历:
-
- 前序遍历:递归实现
- 中序遍历:递归实现
- 后序遍历:递归实现
- 层序遍历:队列实现
- 先序遍历和中序遍历确定一颗二叉树:
- 树的同构:
- 二叉树的表示:静态链表
-
- 建树:
- 判断两棵树是否同构:
- 二叉搜索树:
-
- 判断是否为同一颗二叉搜索树:
线性结构:多项式加法(链表实现)
```c++
#include二叉树:
二叉树的储存:链表储存
二叉树的储存结构
typedef struct TreeNode *BinTree;
typedef BinTree Position;
struct TreeNode{
ElementType Data;
BinTree Left;//左儿子
Bintree Right;//右儿子
};
二叉树的遍历:
前序遍历:递归实现
void PreOrderTraversal(BinTree BT)
{
if(BT){
cout<<BT->Data;
PreOrderTraversal(BT->Left);
PreOrderTraversal(BT->Right);
}
}
中序遍历:递归实现
void InorderTraversal(BinTree BT)
{
if(BT){
InOrderTraversal(BT->Left);
cout<<BT->Data;
InorderTraversal(BT->Right);
}
}
后序遍历:递归实现
void PostOrderTraversal(BinTree BT)
{
if(BT){
PostOrderTraversal(BT->Left);
PostOrderTraversal(BT->Right);
cout<<BT->Data;
}
}
层序遍历:队列实现
1.从队列中取出有个元素2.访问该元素所指的结点3.若该结点所指的左右结点非空则将其左右儿子是指针顺序入队
#include由两种遍历序列确定二叉树必须要有中序遍历!
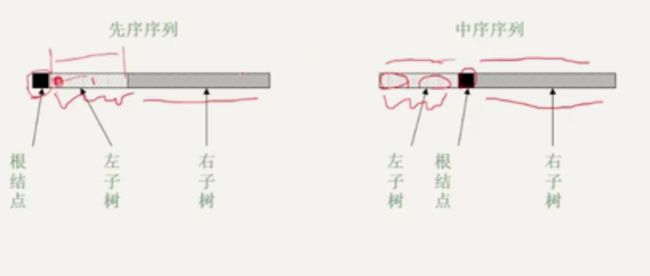
先序遍历和中序遍历确定一颗二叉树:
1.根据先序遍历第一个结点确定根节点
2.根据根节点在中序遍历中分割成左子树和右子树
3.分别递归实现
知前序和中序遍历求后续遍历(hdu1710)
#include树的同构:
两棵树通过若干次左右儿子的互换可变成对方则这两棵树同构
二叉树的表示:静态链表
判断根节点:静态数组里面没有用到的结点即对应的Element为根
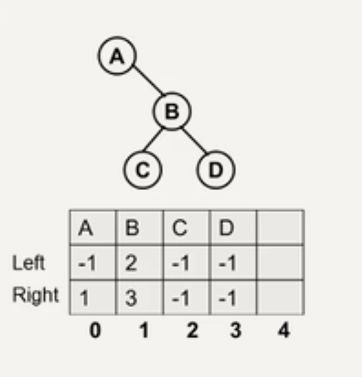
//二叉树的表示:静态链表
#define MaxTree 10
#define ElementType char
#define ELT ElementType
#define Tree int
#define Null -1//区分NULL
struct TreeNode{
ELT Element;
Tree Left;
Tree Right;
}T1[MaxTree],T2[MaxTree];
建树:
Tree BuildTree(struct TreeNode T[])//建树
{
char cl,cr;
int N,check[MaxTree],Root;
cin>>N;
if(N){
for(int i=0;i<N;i++) check[i]=0;
for(int i=0;i<N;i++){
scanf("%c %c %c\n",&T[i].Element,&cl,&cr);
if(cl!='-'){
T[i].Left=cl-'0';
check[T[i].Left]=1;
}
else T[i].Left=Null;
if(cr!='-'){
T[i].Right=cl-'0';
check[T[i].Right]=1;
}
else T[i].Right=Null;
}
for(int i=0;i<N;i++)
if(!check[i]) { Root=i;break;}
}
return Root;
}
判断两棵树是否同构:
#include二叉搜索树:
判断是否为同一颗二叉搜索树:
主要思路:先建一棵树,然后把每个序列分别比较。对于一个序列,如果在查找过程中经过在树上有为被访问过的点则不是一棵树

#include