《数据结构、算法与应用C++语言描述》-队列的应用-电路布线问题

《数据结构、算法与应用C++语言描述》-队列的应用-电路布线问题

问题描述

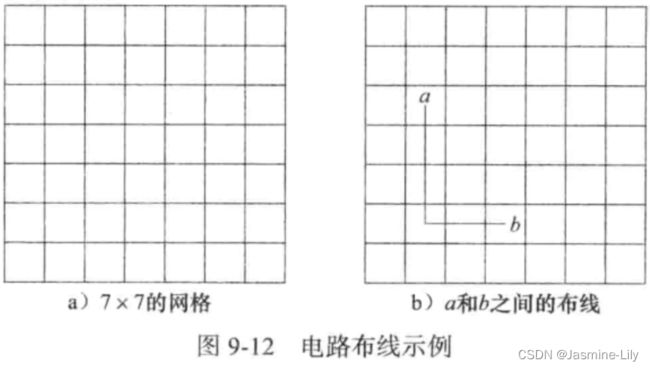
在 迷宫老鼠问题中，可以寻找从迷宫入口到迷宫出口的一条最短路径。这种在网格中寻找最短路径的算法有许多应用。例如，在电路布线问题的求解中，一个常用的方法就是在布线区域设置网格，该网格把布线区域划分成nxm个方格，就像迷宫一样（如图 9-12a 所示）。一条线路从一个方格 a 的中心点连接到另一个方格 b 的中心点，转弯处可以采用直角，如图 9-12b 所示。已经有线路经过的方格被“封锁”，成为下一条线路的障碍。我们希望用a 和 b之间的最短路径来布线，以减少信号的延迟。

求解策略

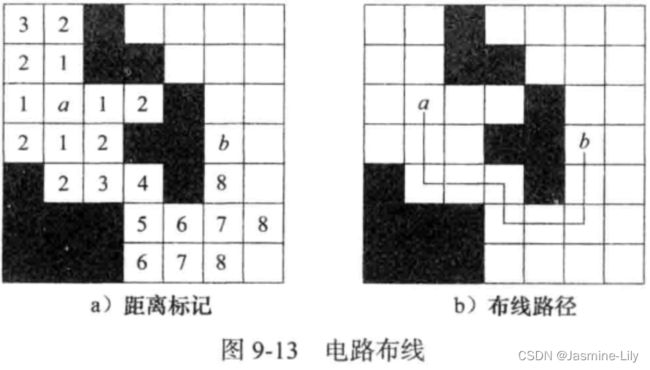
a和b之间的最短路径需要在两个过程中确定。一个是距离标记过程，另一个是路径标记过程。在距离标记过程中，先从位置a开始，把从a可到达的相邻方格都标记为1（表示与a相距为1），然后把从编号为1的方格可到达的相邻方格都标记为2（表示与a相距为2）。这个标记过程继续下去，直至到达b或者没有可到达的相邻方格为止。图9-13a 显示了这种搜索过程的结果，其中 a=（3，2），b=（4，6）。图中的阴影部分是被封锁的方格。

一旦到达 b，b 的编号便是 b 与 a之间的距离（在图 9-13a 中，b上的标号为 9）。距离标记过程结束之后，路径标记过程开始。从方格 b 开始，首先移动到一个其编号比b的编号小1的相邻方格上。在图9-13a中，我们从b移到方格（5，6）。接下来，从方格（5，6）移到比当前编号小 1 的相邻位置上。重复这个过程，直至到达 a 为止。在图 9-13a 的例子中，从（5，6），然后移到（6，6）、（6，5）、（6，4）、（5，4），等等。图 9-13b 给出了所得到的路径，它是（3，2）和（4，6）之间的最短路径。注意，最短路径不是唯一的，（3，2）、（3，3）、（4，3）、（5，3）、（5，4）、（6，4）、（6，5）、（6，6）、（5，6）、（4，6）是另一条最短路径。

代码

#include 
#include 
using namespace std;

/*用于存储迷宫地址的结构体*/
struct Position
{
    int row,  //行
    col;  //列
    Position() {}
    Position(int prow, int pcol):row(prow),col(pcol){}
    operator int() const { return row; }
    friend ostream& operator<<(ostream& out, const Position x)
    {
        out << "(" << x.row << "," << x.col << ")";
        return out;
    }
};
/*创建二维数组*/
template <class T>
bool make2dArray(T**& x, int numberOfRows, int numberOfColumns)
{
    try {
        //行指针
        x = new T * [numberOfRows];
        //为每一行分配内存
        for (int i = 0; i < numberOfRows; i++)
            x[i] = new int[numberOfColumns];
        return true;
    }
    catch (bad_alloc) { return false; }
}

/*遍历二维数组*/
template<class T>
void traverse2dArray(T**& x, int numberOfRows, int numberOfColumns)
{
    for (int i = 0; i < numberOfRows; i++)
    {
        for (int j = 0; j < numberOfColumns; j++)
        {
            cout.width(4);
            cout << x[i][j] << "  ";
        }
        cout << endl;
    }
}

/*电路布线问题全局变量*/
int** Grid;//二维方阵
int GridSize;//方阵大小
queue<Position> path;//记录路径的队列
/*电路布线---和迷宫老鼠问题有点像*/
/*方格元素为1表示为障碍，方格元素为0表示无障碍*/
/*方格标记为2表示是起点，方格标记为大于2的整数m表示该方格距离起点m-2步*/
void inputGridQueue()//输入迷宫
{
    cout << "Please enter the size of Grid-Matrix:";
    while (!(cin >> GridSize))
    {
        cin.clear();//清空标志位
        while (cin.get() != '\n')//删除无效的输入
            continue;
        cout << "Please enter the size of Grid-Matrix:";
    }
    //+2的原因是为了避免在处理内部位置和边界位置时存在差别
    make2dArray<int>(Grid, GridSize + 2, GridSize + 2);
    //初始化边界位置的数值
    for (int i = 0; i <= GridSize + 1; i++)
    {
        Grid[i][0] = 1;
        Grid[0][i] = 1;
        Grid[i][GridSize + 1] = 1;
        Grid[GridSize + 1][i] = 1;
    }
    //初始化迷宫
    for (int i = 1; i <= GridSize; i++)
        for (int j = 1; j <= GridSize; j++)
        {
            int positionij;
            cout << "Please enter Grid[" << i << "," << j << "]:";
            while (!(cin >> positionij))
            {
                cin.clear();//清空标志位
                while (cin.get() != '\n')//删除无效的输入
                    continue;
                cout << "Please enter Grid[" << i << "," << j << "]:";
            }
            Grid[i][j] = positionij;
        }
    cout << "The Grid = " << endl;
    traverse2dArray<int>(Grid, GridSize + 2, GridSize + 2);
}
bool findPathQueue(Position start,Position end)//寻找从起点到终点的最短路径，如找到返回true，如没找到则返回false
{
    if ((start.row == end.row) && (start.col == end.col))
        return true;
    //初始化偏移量
    Position offset[4];
    offset[0].row = 0; offset[0].col = 1;//右
    offset[1].row = 1; offset[1].col = 0;//下
    offset[2].row = 0; offset[2].col = -1;//左
    offset[3].row = -1; offset[3].col = 0;//上
    Position here = start;
    Grid[start.row][start.col] = 2;//标记起点为2
    int numOfNbrs = 4;//一个方格的相邻位置数
    /*标记各个方格*/
    queue<Position> q;//将需要标记的方格入栈q
    Position nbr;//邻居方格
    while (true)
    {
        //给相邻位置做标记
        for (int i = 0; i < numOfNbrs; i++)
        {
            nbr.row = here.row + offset[i].row;
            nbr.col = here.col + offset[i].col;
            if (Grid[nbr.row][nbr.col] == 0)//只有方格为0时表示方格无障碍和未标记
            {
                Grid[nbr.row][nbr.col] = Grid[here.row][here.col] + 1;
                if ((nbr.row == end.row) && (nbr.col == end.col))
                    break;//如果标记到终点，则标记完成
                q.push(nbr);//把邻居结点插入队列，以备后面标记，也就是找邻居的邻居
            }
        }
        if ((nbr.row == end.row) && (nbr.col == end.col))
            break;//如果标记到终点，则标记完成
        if (q.empty())
            return false;//没有找到终点，则不可达，返回false
        here = q.front();//取队首元素作为下一节点，以备标记其邻居节点
        q.pop();//删除队首节点
    }

    /*标记完成，构造路径*/
    int pathLength = Grid[end.row][end.col] - 2;
    here = end;//从终点开始回溯
    for (int i = pathLength - 1; i >= 0; i--)
    {
        path.push(here);
        for (int j = 0; j < numOfNbrs; j++)//在周边寻找父节点
        {
            nbr.row = here.row + offset[j].row;
            nbr.col = here.col + offset[j].col;
            if (Grid[nbr.row][nbr.col] == i + 2)
                break;
        }
        here = nbr;
    }
    path.push(start);
    return true;
}
void outputPathQueue()//输出路径
{
    int i = 0;
    cout << "The path = ";
    while(!path.empty()){
        cout << path.front() << ", ";
        path.pop();
    }
    cout << endl;
}

void routingOfCircuit()//测试函数
{
    inputGridQueue();//输入迷宫
    /*输入起始值点和终点*/
    Position start, end;
    cout << "Please enter the start node:";
    while (!(cin >> start.row >> start.col))
    {
        cin.clear();//清空标志位
        while (cin.get() != '\n')//删除无效的输入
            continue;
        cout << "Please enter the start node:";
    }
    cout << "Please enter the end node:";
    while (!(cin >> end.row >> end.col))
    {
        cin.clear();//清空标志位
        while (cin.get() != '\n')//删除无效的输入
            continue;
        cout << "Please enter the end node:";
    }
    findPathQueue(start, end);//寻找最短路径，如找到返回true，如没找到则返回false
    outputPathQueue();//输出路径
}

int main()
{
    cout << "电路布线问题********************" << endl;
    routingOfCircuit();

    return 0;
}

运行结果

C:\Users\15495\Documents\Jasmine\Work\coding\cmake-build-debug\coding.exe
鐢佃矾甯冪嚎闂********************
Please enter the size of Grid-Matrix:7
Please enter Grid[1,1]:0
Please enter Grid[1,2]:0
Please enter Grid[1,3]:1
Please enter Grid[1,4]:0
Please enter Grid[1,5]:0
Please enter Grid[1,6]:0
Please enter Grid[1,7]:0
Please enter Grid[2,1]:0
Please enter Grid[2,2]:0
Please enter Grid[2,3]:1
Please enter Grid[2,4]:1
Please enter Grid[2,5]:0
Please enter Grid[2,6]:0
Please enter Grid[2,7]:0
Please enter Grid[3,1]:0
Please enter Grid[3,2]:0
Please enter Grid[3,3]:0
Please enter Grid[3,4]:0
Please enter Grid[3,5]:1
Please enter Grid[3,6]:0
Please enter Grid[3,7]:0
Please enter Grid[4,1]:0
Please enter Grid[4,2]:0
Please enter Grid[4,3]:0
Please enter Grid[4,4]:1
Please enter Grid[4,5]:1
Please enter Grid[4,6]:0
Please enter Grid[4,7]:0
Please enter Grid[5,1]:1
Please enter Grid[5,2]:0
Please enter Grid[5,3]:0
Please enter Grid[5,4]:0
Please enter Grid[5,5]:1
Please enter Grid[5,6]:0
Please enter Grid[5,7]:0
Please enter Grid[6,1]:1
Please enter Grid[6,2]:1
Please enter Grid[6,3]:1
Please enter Grid[6,4]:0
Please enter Grid[6,5]:0
Please enter Grid[6,6]:0
Please enter Grid[6,7]:0
Please enter Grid[7,1]:1
Please enter Grid[7,2]:1
Please enter Grid[7,3]:1
Please enter Grid[7,4]:0
Please enter Grid[7,5]:0
Please enter Grid[7,6]:0
Please enter Grid[7,7]:0
The Grid =
   1     1     1     1     1     1     1     1     1
   1     0     0     1     0     0     0     0     1
   1     0     0     1     1     0     0     0     1
   1     0     0     0     0     1     0     0     1
   1     0     0     0     1     1     0     0     1
   1     1     0     0     0     1     0     0     1
   1     1     1     1     0     0     0     0     1
   1     1     1     1     0     0     0     0     1
   1     1     1     1     1     1     1     1     1
Please enter the start node:3 2
Please enter the end node:4 6
The path = (4,6), (5,6), (6,6), (6,5), (6,4), (5,4), (5,3), (5,2), (4,2), (3,2),

Process finished with exit code 0

离线等价类问题