牛客前200道题文字解
牛客前200道题文字解
- 一、反转链表:
- 二、排序
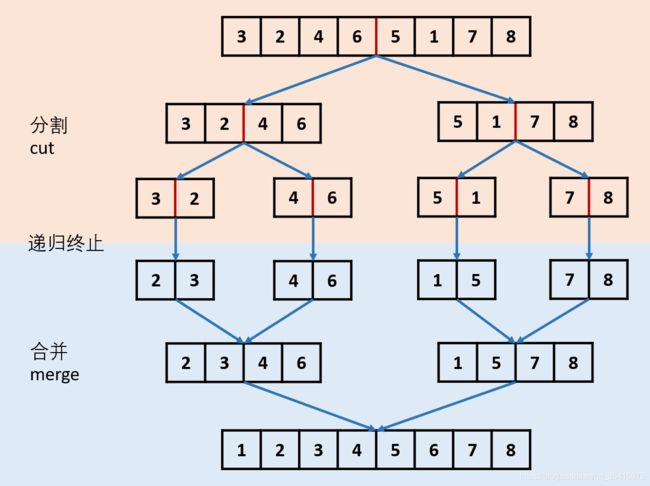
- 归并排序
- 三、二叉树的先序中序后序遍历
- 四、最小的K个数
- 五、二分查找(从小到大数组)
- 六、二叉树层序遍历
- 七、俩数之和
- 八、括号匹配问题
- 九、合并有序链表(通过断开链表节点的方式)
- 十、用俩个栈实现队列
- 十一、跳台阶(菲契那波数列)
- 十二、链表中的节点每k个一组反转
- 十三 、最长回文子串
- 十四、删除链表的倒数第n个指针
- 十五、最长无重复子串(子串是连续的)
- 十六、判断链表是否有环
- 十七、合并俩个有序数组
- 十八、对于一个给定的链表,返回环的入口节点,如果没有环,返回null
- 十九、大数相加(字符串模拟加减法)
- 二十、NMS
- 二十一、iou
- 二十二、rand()生成随机数
- 二十三、二叉树之字形遍历
- 二十四、最长公共子串
- 二十五、给出一个有n个元素的数组S,S中是否有元素a,b,c满足a+b+c=0?找出数组S中所有满足条件的三元组。
- 二十六、求平方根
- 二十七、找转动数组位置
- 二十八、合并k个有序链表(难题,不看)
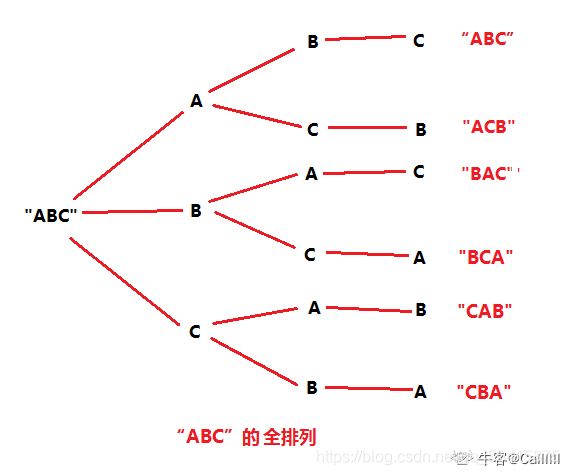
- 字符串全排列
- 二十九、容器盛水
- 三十、二叉树的右视图
- 三十一、岛屿数量
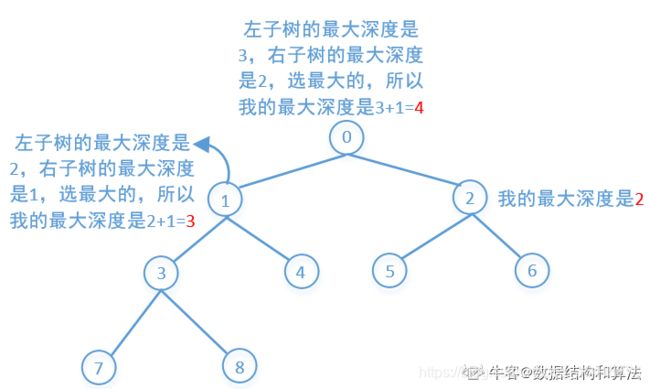
- 三十二、二叉树的最大深度
- 三十三、 判断回文
- 三十四、链表排序
- 三十五、判断是平衡二叉树
- 三十六、数组中出现次数超过一半的数字
- 三十七、寻找第k大
- 三十八、链表相加
- 三十九、二叉树重建
- 四十、矩阵的最小路径和
- 四十一、最大数
- 四十二、圆圈中最后剩下的数(约瑟夫环)
- 四十三、出现次数topk问题
- 四十四、进制转换
- 四十五、二叉树的所有路径和
- 四十六、矩阵元素查找
- 五十、缺失数字
- 五十一、链表的奇偶重排
- 五十二、列表中逆序对
- 五十四、优美数
- 五十五、打印给定长度的所有路径
- 五十六、 俩个链表交叉,判断交叉点
- 五十七、二叉树最大路径和
- 五十八、 判断二叉树是否对称
- 五十九、数字转换为ip地址
- 六十、重排链表
- 六十一、有重复数字的所有排列
- 六十二、最长括号子串
- 六十三、回文数字
- 六十四、丢棋子问题
- 六十五、二叉搜索树的第k个节点
- 六十六、约瑟夫环
- 六十七、链表中倒数第k个节点
- 六十八、二进制中1的个数
- 六十九、最大正方形
- 七十、字典树的实现
- 七十一、二叉树每层打印
- 七十二、子数组最大乘积
- 七十三、调整数组使奇数位于偶数前面(且相对位置不能改变)
- 七十四、合并二叉树
- 七十五、矩阵最长递增路径
- 七十六、有序数组转换为平衡二叉树
- 七十七、扑克牌排序
- 七十八、旋转数组中的最小数
- 七十九、最长重复数字
- 八十、最近公共祖先
- 八十一、螺旋矩阵
- 八十二、在旋转过的有序数组中寻找目标值
- 八十三、数据中的中位数
struct TreeNode
{
int val;
struct TreeNode *left;
struct TreeNode *right;
};
一、反转链表:
核心:
将原来链表的一个节点断出来后当作新链表的头
具体核心:
new_head(新链表尾)
cur(原来链表游标)
head(原链表头)
节点与原链表断开后,将新链表头连接到该节点之后,实现过程为俩个指针,一个指针负则断开,一个指针负责往后指。
head负责原指针向后指向,cur负责断开
new_head = NULL
while(head){
cur=head//头节点保存
head = head ->next//头节点后移
cur->next = NULL//断开
//到这步成功将节点断开,并且指针后移
cur->next = new_head//新链表头连断出节点的尾
new_head = cur//头更新
}
return new_head 或者return cur都可
二、排序
核心:快速排序
具体核心:
首先以第一个位置的元素为标志,向后寻找,left从下一个元素开始找找,到大于该元素的元素left停止,right从最后一个元素向左寻找,找到小于该元素的元素right停止,然后俩者互换位置,继续寻找,直到left和right相遇,将left所在元素和第一个元素相交换位置,然后左右分开的俩段,继续递归执行相同的操作,直到分的段的长度为1,停止然后返回,得到的数组就是排好序的数组。
def quick_sort(ary):
return qsort(ary,0,len(ary)-1)
def qsort(ary,left,right):
#快排函数,ary为待排序数组,left为待排序的左边界,right为右边界
if left >= right : return ary
key = ary[left] #取最左边的为基准数
lp = left #左指针
rp = right #右指针
while lp < rp :
while ary[rp] >= key and lp < rp :#右边一直向左寻找,找到第一个不比基准数大的就停止
rp -= 1
while ary[lp] <= key and lp < rp :#左边一直向右寻找,找到第一个不比基准数小的就停止
lp += 1
ary[lp],ary[rp] = ary[rp],ary[lp]#将停止后的(即是满足交换的数组元素进行位置交换)
ary[left],ary[lp] = ary[lp],ary[left]#找到基数位置并且进行交换
qsort(ary,left,lp-1)#基准数左边(不包括基准数)
qsort(ary,rp+1,right)#基准数右边(不包括基准数)
return ary
归并排序
def merge_sort(alist):
n = len(alsit)
if n <= 1:#如果拆分到是一个元素,那么返回这个元素即可
return alist
mid = n//2#以mid拆分alist
left_li = merge_sort(alsit[:mid])#递归拆分的左半段
right_li = merge_sort(alsit[mid:])#递归拆分的右半段
left_pointer,right_pointer =0,0#指向左半段的指针left_pointer(int类型),指向右半段的指针right_pointer(int类型)
result = []#合并的结果
while left_pointer三、二叉树的先序中序后序遍历
核心:print(root)的位置决定是哪种遍历
具体核心:
先序:中左右
中序:左中右
后续:左右中
def printTree(root):
printTree(root->left)
printTree(root->right)
print(root.val)
四、最小的K个数
核心:堆排序
具体核心:
先写局部最小堆函数minHeap(a, i, heapSize),a是数组,i是第i个节点,heapsize是堆的大小
再调用局部最小堆函数创建全局小根堆
局部最小堆函数的核心是:
首先将i节点的左右子节点分别于i节点进行比较大小,如果i就是最大的则程序结束,如果不是则将最大的和i节点进行交换,然后将交换后的节点递归执行minHeap()函数。
建立全局最小堆的核心是
void buildMaxHeap(vector& a, int heapSize) {
for (int i = heapSize / 2; i >= 0; --i) {\*heapsize/2整除,直接找到堆的最小的不是叶子节点的节点,这样一来最先就是从堆的底端开始。这一点很重要,是自底向上的构建大根堆\*
maxHeapify(a, i, heapSize);\*调用局部大根堆函数*
}
}
def heap_sort(ary) :
n = len(ary)
first = int(n/2-1) #最后一个非叶子节点
for start in range(first,-1,-1) : #构造大根堆
max_heapify(ary,start,n-1)
for end in range(n-1,0,-1): #堆排,将大根堆转换成有序数组
ary[end],ary[0] = ary[0],ary[end]
max_heapify(ary,0,end-1)
return ary
#最大堆调整:将堆的末端子节点作调整,使得子节点永远小于父节点
#start为当前需要调整最大堆的位置,end为调整边界
def max_heapify(ary,start,end):
root = start
while True :
child = root*2 +1 #调整节点的子节点
if child > end : break
if child+1 <= end and ary[child] < ary[child+1] :
child = child+1 #取较大的子节点
if ary[root] < ary[child] : #较大的子节点成为父节点
ary[root],ary[child] = ary[child],ary[root] #交换
root = child
else :
break
本题代码
核心:优先队列就是大根堆
具体核心:先push input k个节点进来,input[i]与优先队列的top进行比较如果比top小,就将头pop,然后将input[i]压入,这个过程优先队列会自动维持大根堆。
class Solution {
public:
vector GetLeastNumbers_Solution(vector input, int k) {
vector ret;
if (k==0 || k > input.size()) return ret;
priority_queue> pq;
for (const int val : input) {
if (pq.size() < k) {
pq.push(val);
}
else {
if (val < pq.top()) {
pq.pop();
pq.push(val);
}
}
}
while (!pq.empty()) {
ret.push_back(pq.top());
pq.pop();
}
return ret;
}
};
五、二分查找(从小到大数组)
核心:找到中间值,与查找元素比对,四个参数
具体核心:
函数:binarySearch(a,left,right,val)
首先通过:mid=left+right//2找到中间元素下标
如果找到待找元素则return mid
如果待找元素比mid大则执行(a,mid+1,right,val)
如果待招元素比mid小则执行(a,left,mid-1,val)
直到left>right 则return -1
# 返回 x 在 arr 中的索引,如果不存在返回 -1
def binarySearch (arr, l, r, x):
# 基本判断
if r >= l:
mid = int(l + (r - l)/2)
# 元素整好的中间位置
if arr[mid] == x:
return mid
# 元素小于中间位置的元素,只需要再比较左边的元素
elif arr[mid] > x:
return binarySearch(arr, l, mid-1, x)
# 元素大于中间位置的元素,只需要再比较右边的元素
else:
return binarySearch(arr, mid+1, r, x)
else:
# 不存在
return -1
六、二叉树层序遍历
核心:队列,广度优先
具体核心:
将根节点加入队列,当队列不为空则将队列首元素pop,然后判断pop出来的元素的左右元素是否是NULL,不是则加入队列尾,然后只要队列不为空就一直循环这个步骤,直到队列为空,层序遍历结束。
def breadth_travel(root):
if root is None:
return 0
queue = [self.root]
while queue is not None:
cur_node = queue.pop(0)#先进去的先出来
print(cur_node.elem)
if cur_node.lchild is not None:#队列出去一位的子节点排在队列末尾
queue.append(cur_node.lchild)#左节点先进队列末尾
if cur_node.rchild is not None:
queue.append(cur_node.rchild)#右节点先进队列末尾
七、俩数之和
核心:target-num ,使用哈希表查找符合
具体核心:
首先将所有数字存储进入到map 的key值中,下标存储到对应的val中,然后遍历数组所有数字,每次找是否右key==target-num,如果找到则直接returnval和i,如果没找到则继续寻找。
class Solution {
public:
/**
*
* @param numbers int整型vector
* @param target int整型
* @return int整型vector
*/
vector twoSum(vector& numbers, int target) {
vectorres;//保存结果
mapmp;//定义一个哈希表存储numbers[i]和对应的下标
for (int i = 0; i < numbers.size(); i ++) {//进行标记
mp[numbers[i]] = i;
}
for (int i = 0; i < numbers.size(); i++) {
//每遍历一个numbers[i]就去对应的mp里找有没有target - numbers[i]
//如果有就返回结果
//如果没有就找下一个
if(mp.find(target - numbers[i]) != mp.end() && i != mp[target - numbers[i]]){
res.push_back(i + 1);
res.push_back(mp[target - numbers[i]] + 1);
return res;
}
}
return res;
}
};
八、括号匹配问题
核心:利用栈的特点,先进后出
具体核心:
当stack为空,将s[i]压入栈,如果stack不是空的,则s[i]与stack.top()比较,如果s[i]与stack的top是匹配的,那么就把stack.pop(),如果不匹配则继续将s[i]压入stack,如果最后s遍历完,stack是空的就是标准括号,否则就是不符合规则的括号。
class Solution {
public:
bool isValid(string s) {
stack c;
for(int i = 0 ; i < s.length(); i++)
{
if(c.empty())
{
c.push(s[i]);
continue;
}
if(s[i]==')'&&c.top()=='('){c.pop();}
else if(s[i]=='}'&&c.top()=='{'){c.pop();}
else if(s[i]==']'&&c.top()=='['){c.pop();}
else{ c.push(s[i]);}
}
return c.empty();
}
};
九、合并有序链表(通过断开链表节点的方式)
核心:链表的操作,游标
具体核心:
首先将俩个链表的当前游标所在位置进行比较,将小的一方的游标向后移动,直到比另一方大停止,将该节点之前的链表连接在新链表的尾端,循环这个步骤,直到某一方链表遍历结束。
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
class Solution {
public:
/**
*
* @param l1 ListNode类
* @param l2 ListNode类
* @return ListNode类
*/
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
// write code here
if(l1 == NULL) return l2; //如果l1为空返回l2
if(l2 == NULL) return l1;//如果l2为空返回l1
ListNode *res = new ListNode(-1);//创建res链表用于返回最终结果链表
ListNode *pre = res;//pre的作用是进行链表的合并
while(l1 != NULL && l2 != NULL){
if(l1->val < l2->val){ //如果l1.val < l2.val 就让当前l1节点进入res
pre->next = l1;
l1 = l1->next;
}else{//如果l1.val > l2.val 就让当前l2节点进入res
pre->next = l2;
l2 = l2->next;
}
pre = pre->next;//pre指针移动到下一个
}
pre->next = l1 == NULL?l2:l1;//将不为空的那个没有遍历完的链表部分直接插入
return res->next;//因为头指针为-1所以直接返回头指针的下一个节点
}
};
十、用俩个栈实现队列
核心:一个栈负责队列入,一个栈负责队列的出
具体核心:当加入一个元素时候将其直接加入到stack1中,当需要取出一个元素时候,将stack1中所有元素放入stack2中并且将stack2的顶元素取出。当继续有元素加入时,加入的元素应该是在stack2中元素的最后一个元素后才出队列,因此,加入时候直接加入stack1,出的时候,只有当stack2为空的时候,才可以将stack1的全部元素加入到stack2中。
总结:加入的时候直接加入stack1,出的时候分俩种情况,一种是stack2为空,则将stack1全部加入stack2然后从stack2弹出,如果stack2不为空,则将stack2的顶元素弹出即可。
class Solution
{
public:
void push(int node) {
stack1.push(node);
}
int pop() {
if (stack2.empty()) {
while (!stack1.empty()) {
stack2.push(stack1.top());
stack1.pop();
}
}
int ret = stack2.top();
stack2.pop();
return ret;
}
private:
stack stack1;
stack stack2;
};
十一、跳台阶(菲契那波数列)
核心:递归
具体核心:
int Fibonacci(int n) {
if (n<=1) return 1;
return Fibonacci(n-1) + Fibonacci(n-2);
}
十二、链表中的节点每k个一组反转
题目:
给定的链表是1→2→3→4→5
对于 k=2, 你应该返回 2→1→4→3→5
对于 k=3, 你应该返回 3→2→1→4→5
核心:将前k个节点先于原链表断开,然后将前半断反转后在进行连接
具体核心:
反转链表是核心,节点与原链表断开后,将新链表头连接到该节点之后,实现过程为俩个指针,一个指针负则断开,一个指针负责往后指。
class Solution {
public:
ListNode* reverse(ListNode * head,k)
{
ListNode * cur,new_head,new2_head,tail;
cur = head;
for(int i = 1;inext;
}
new2_head = cur->next;//断开链表后半段头节点
cur->next = nullptr;//先把前k个节点断开
tail = head;//之后得连在前半段反转后的尾,也就是反转前的头
while(head){//反转断出来的链表
cur=head;//头节点保存
head = head ->next;//头节点后移
cur->next = nullptr;//断开
//到这步成功将节点断开,并且指针后移
cur->next = new_head;//新链表头连断出节点的尾
new_head = cur//头更新
}
tail->next=new2_head;
return new_head;
}
十三 、最长回文子串
核心:中心扩散
具体核心:遍历每一个字符,从每一个字符向左右扩展,每次都从第i个字符向俩边扩展,left–,right++,left要大于0,right要小于数组长度,遍历完成找出最大的即可,注意中心有俩种,一种是一个字符是中心,一种是俩个字符为中心。
class Solution:
def longestPalindrome(self, s):
left = 0
right = 0
n = len(s)
p1 = p2 = ''
# 双指针,遍历两遍
while(right-1 and s[left:right+1] == s[left:right+1][::-1]:
p1 = s[left:right+1]
# 当当前子串是回文时,增加下一个要找的子串的长度
right += 1
left -= 1
else:
right += 1
left += 1
left = 0
right = 1
while(right-1 and s[left:right+1] == s[left:right+1][::-1]:
p2 = s[left:right+1]
right += 1
left -= 1
else:
right += 1
left += 1
return p1 if len(p1)>len(p2) else p2
十四、删除链表的倒数第n个指针
核心:快慢指针
具体核心:快指针比慢指针要快K个节点,当快指针到达尾的时候,慢指针到达倒数第k个节点,然后进行链表的删除操作即可。
十五、最长无重复子串(子串是连续的)
核心:双指针,计只要没发现重复一直向后,计算俩指针的距离差。
具体核心:我们使用两个指针,一个i一个j,最开始的时候i和j指向第一个元素,然后i往后移,把扫描过的元素都放到map中,如果i扫描过的元素没有重复的就一直往后移,顺便记录一下最大值max,如果i扫描过的元素有重复的,就改变j的位置到当前i的位置,然后重复上述过程,直到i到达末尾。

int maxLength(int[] arr) {
if (arr.length == 0)
return 0;
map mp ;
int max = 0;
int j = 0;
for (int i = 0; i < arr.length; i++) {
if (mp.find(arr[i])!=mp.end()) {
max =max(max, i - j + 1);
j =i ;
}
map[arr[i]]= i;
}
return max;
}
十六、判断链表是否有环
核心:快指针每次走俩步,慢指针每次走一步
具体核心:都从头节点开始,快指针每次走俩步fast = fast->next->next,慢指针每次走一步slow = slow->next,直到slow == fast,说明有环,注意fast和fast->next都不可以是nullptr。
使用快慢指针而不是直接将head存储然后再遇到head表示有环是因为上面1,2这种情况。
bool hasCycle(ListNode* head) {
if (head == nullptr)
return false;
//快慢两个指针
ListNode* slow = head;
ListNode* fast = head;
while (fast != nullptr && fast->next != nullptr) {
//慢指针每次走一步
slow = slow->next;
//快指针每次走两步
fast = fast->next->next;
//如果相遇,说明有环,直接返回true
if (slow == fast)
return true;
}
//否则就是没环
return false;
}
十七、合并俩个有序数组
核心:将俩个数组分别比较将大的元素放入新数组中然后指针向后移动
具体核心:A_point指向数组A,B_point指向数组B,将A[A_point]和B[B_point]进行比较,将较大的赋值给新数组C,并且对应的A_point或者B[point]向后移动,b<0||(a>=0&&A[a]>=B[b]),注意该句可以使得一方数组到末尾后将另一数组剩下的直接加到新数组C。
class Solution {
public:
void merge(int A[], int m, int B[], int n) {
//因为题目明确说了A数组足够大,所以直接在A数组操作
int i = m - 1;
int j = n - 1;
int index = m + n - 1;//AB合并后最后一个元素所在位置
while(i >= 0 && j>= 0)//AB合并,谁大就先放谁
A[index --] = A[i] > B[j] ? A[i --] : B[j --];
while(j >= 0)//如果B没有遍历完,那么之间丢在A数组里面
A[index--] = B[j --];
}
};
十八、对于一个给定的链表,返回环的入口节点,如果没有环,返回null

核心:快慢指针
具体核心:快指针与慢指针均从X出发,在Z相遇。此时,慢指针行使距离为a+b,快指针为a+b+n(b+c)。所以2*(a+b)=a+b+n*(b+c),推出
a=(n-1)b+nc=(n-1)(b+c)+c;得到,将此时两指针分别放在起始位置和相遇位置,并以相同速度前进,当一个指针走完距离a时,另一个指针恰好走出 绕环n-1圈加上c的距离。实现黑体部分内容,关键在于引入新的指针slow2。
while(fast!=null&&fast.nest!=null){
fast=fast.next.next
slow=slow.next;
if(fast==slow){ //利用快慢指针找相遇点
ListNode slow2=head; //设置以相同速度的新指针从起始位置出发
while(slow2!=slow){ //未相遇循环。
slow=slow.next;//
slow2=slow2.next;
}
return slow;
}
十九、大数相加(字符串模拟加减法)
没啥操作估计不考
二十、NMS
给定一个长度为N的列表A,列表中的每一个元素都是一个bounding box,(min_row,min_col,max_row,max_col)。
同时给定一个长度为N的列表B,列表中每个元素都是列表A中相应bounding box的置信度。请用非极大值抑制算法对bounding box进行过滤
def nms(A, thresh,B):
x1 = A[:, 0] #xmin
y1 = A[:, 1] #ymin
x2 = A[:, 2] #xmax
y2 = A[:, 3] #ymax
scores = B#confidence
areas = (x2 - x1 + 1) * (y2 - y1 + 1) # 每个boundingbox的面积
order = scores.argsort()[::-1] # boundingbox的置信度排序
keep = [] # 用来保存最后留下来的boundingbox
while order.size > 0:
i = order[0] # 置信度最高的boundingbox的index
keep.append(i) # 添加本次置信度最高的boundingbox的index
# 当前bbox和剩下bbox之间的交叉区域
# 选择大于x1,y1和小于x2,y2的区域
xx1 = np.maximum(x1[i], x1[order[1:]]) #交叉区域的左上角的横坐标
yy1 = np.maximum(y1[i], y1[order[1:]]) #交叉区域的左上角的纵坐标
xx2 = np.minimum(x2[i], x2[order[1:]]) #交叉区域右下角的横坐标
yy2 = np.minimum(y2[i], y2[order[1:]]) #交叉区域右下角的纵坐标
# 当前bbox和其他剩下bbox之间交叉区域的面积
w = np.maximum(0.0, xx2 - xx1 + 1)
h = np.maximum(0.0, yy2 - yy1 + 1)
inter = w * h
# 交叉区域面积 / (bbox + 某区域面积 - 交叉区域面积)
ovr = inter / (areas[i] + areas[order[1:]] - inter)
#保留交集小于一定阈值的boundingbox
inds = np.where(ovr <= thresh)[0]
order = order[inds + 1]
return keep
二十一、iou
题目:有两个框,设第一个框的两个关键点坐标:(a.x1,a.y1)(a.x2,a.y2),第二个框的两个关键点坐标:(b.x1,b.y1)(b.x2,b.y2),
核心:交有四种情况,一个不动,另一个和它交,有四种位置情况,左上,左下,右上,右下。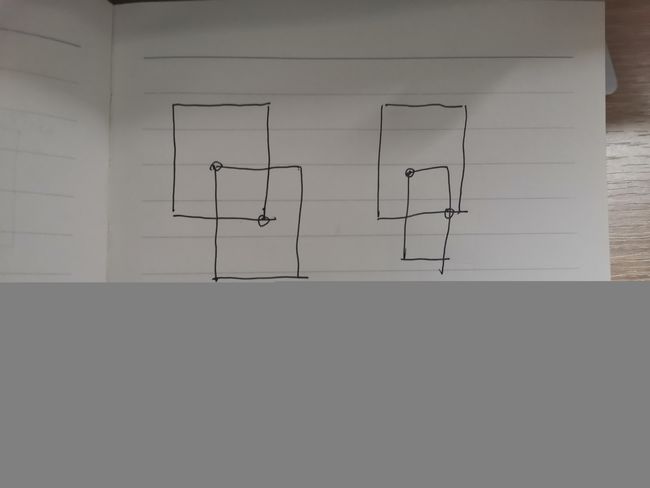
要求图中⚪所在的坐标位置,左上角⚪位置x坐标为box1和box2中左上角横坐标最大的坐标,y坐标为box1和box2左上角纵坐标最小的坐标。右下角⚪位置x坐标为box1和box2中右下角横坐标最小的坐标,y坐标为box1和box2中右下角纵坐标最大的坐标。
struct box {
float x1, y1, x2, y2;
box(float a, float b, float c, float d) :x1(a), y1(b), x2(c), y2(d) {}
};
float box_iou(box a, box b) {
float xx1 = max(a.x1, b.x1);
float yy1 = min(a.y1, b.y1);
float xx2 = min(a.x2, b.x2);
float yy2 = max(a.y2, b.y2);//四种情况通过max和min的关系全部包含
float areaa = (a.x2 - a.x1)*(a.y2 - a.y1);
float areab = (b.x2 - b.x1)*(b.y2 - b.y1);
float ovr = max(float(0), xx2 - xx1)*max(float(0), yy2 - yy1);
return ovr / (areaa + areab - ovr);
}
二十二、rand()生成随机数
题目:已有方法 rand7 可生成 1 到 7 范围内的均匀随机整数,试写一个方法 rand10 生成 1 到 10 范围内的均匀随机整数。
核心:等概率
具体核心:
现在要从 rand7() 到 rand10(),也要求是等概率的,那只要我们把小的数映射到一个大的数就好办了,那首先想到的办法是乘个两倍试一试,每个 rand7() 它能生成数的范围是 1~7,rand 两次,那么数的范围就变为 2~14,哦,你可能发现没有 1 了,想要再减去个 1 来弥补,rand7() + rand7()− 1,其实这样是错误的做法,因为对于数字 5 这种,你有两种组合方式(2+3 or 3+2),而对于 1414,你只有一种组合方式(7+7),它并不是等概率的,那么简单的加减法不能使用,因为它会使得概率不一致,我们的方法是利用乘法,一般思路如下面这样构建:
首先rand7()−1 得到的数的集合为 {0,1,2,3,4,5,6}
再乘 7 后得到的集合 A 为{0,7,14,21,28,35,42}
后面rand7() 得到的集合B为{1,2,3,4,5,6,7}
有人可能会疑惑,你咋不乘 6,乘 5 呢?因为它不是等概率生成,只有乘 7 才能使得结果是等概率生成的,啥意思?我们得到的集合 A 和集合 B,利用这两个集合,得到的数的范围是1~49,每个数它显然是等概率出现的,因为这两个事件是独立事件,如果你不懂什么是独立事件,你试着加加看也能体会一点。
然后又因为40%10生成的数字是0-9,而41-49生成1-9所以只有1-40之间的数字可以用。
代码:
int rand10() {
// 首先得到一个数
int num = (rand7() - 1) * 7 + rand7();
// 只要它还大于40,那你就给我不断生成吧
while (num > 40)
num = (rand7() - 1) * 7 + rand7();
// 返回结果,+1是为了解决 40%10为0的情况
return 1 + num % 10;
}
二十三、二叉树之字形遍历
核心:层序遍历用队列
具体核心:

创建一个队列,首先将根节点添加进去,然后如果队列不空则执行将目前队列的长度计算出,使用for循环,循环次数为当前队列长度,将目前队列中的每个节点的子节点添加进入到队列,然后将目前节点的每个节点都pop,输出,奇数层直接添加子节点到末尾,偶数层插入节点到头。
class Solution {
public:
vector > zigzagLevelOrder(TreeNode* root) {
// write code here
vector >res; //用于存储返回结果
queue q; //创建队列用于存储节点
if(root == NULL) return res; //当为空的时候直接返回
int height = 1; //用于处理之字形遍历,偶数就直接插入,偶数就插入temp头
q.push(root); //插入节点
while(!q.empty()){
vector temp; // 存储每一层的数字
int n = q.size(); // 队列大小表示当前层数的元素个数
for(int i = 0;i < n;i ++){
TreeNode* node = q.front(); //取出队列的第一个元素
q.pop();
if(height % 2 == 0){
temp.insert(temp.begin(),node->val); // 如果层数是偶数就插入到头
}else{
temp.push_back(node->val); //如果层数是奇数就直接放进去
}
if(node->left != NULL) q.push(node->left);//如果左子树不为空就递归左子树
if(node->right!= NULL) q.push(node->right);//如果右子树不为空就递归右子树
}
height ++; //高度++
res.push_back(temp); //把这一层的节点插入到res中
}
return res;
}
};
二十四、最长公共子串
核心:动态规划
具体核心:
思路: 二维数组, 下图:str1: sabgc ,s2:abcg, 二维数组,相同的标记为1 ,不同的标0,可以看出斜对角为1 的就是最长的字串。第一个一样标记1, 第二个对角相同,值应该是dp[x-1],[y-1]下标的值在+1,记录的就是长度。

if (str1 == null || str2 == null || str1.equals(" ") || str2.equals(" ")) {
return "-1";
}
//动态规划 二维数组,斜下来就是最长字串
int str1len = str1.length();
int str2len = str2.length();
int maxLen = 0;
int index = 0;
// 定义一个二维数组
int dp[str1len][str2len];
//第一步:划分
for (int i = 0; i < str1len; i++) {
for (int j = 0; j < str2len; j++) {
if (str1[i]== str2[j]) {
if (j == 0 && i == 0){
dp[i][j]=1;
maxLen = dp[i][j];
index = i;
} else{
dp[i][j] = dp[i - 1][j - 1] + 1;
if(maxLen <= dp[i][j]){
maxLen = dp[i][j];
index = i;
}
}
}
}
}
if( maxLen==0 ){
return "-1";
}
return str1.substr(index-maxLen+1,index+1);//substr左闭右开
二十五、给出一个有n个元素的数组S,S中是否有元素a,b,c满足a+b+c=0?找出数组S中所有满足条件的三元组。
c.begin(); 返回指向容器 最开始位置数据的指针
c.end(); 返回指向容器最后一个数据单元+1的指针
如果我们要输出最后一个元素的值应该是 *(–c.end());
核心:先排序,然后以第一个值为基准开始遍历,用双指针求第二个值和第三个值。
class Solution {
public:
vector > threeSum(vector &num) {
sort(num.begin(), num.end());
vector > res;
if (num.size() < 3) return res;
for (int i = 0; i < num.size() - 2; ++i) {
int j = i + 1;
int k = num.size() - 1;
int target = -num[i];
while (j < k) {
if (num[j] + num[k] > target) --k;
else if (num[j] + num[k] < target) ++j;
else {
vector current = {num[i], num[j], num[k]};
res.push_back(current);
while (j + 1 < k && num[j+1] == num[j]) ++j; // 防止重复
while (k - 1 > j && num[k-1] == num[k]) --k; // 防止重复
++j; --k;
}
}
while (i + 1 < num.size() - 2 && num[i+1] == num[i]) ++i; // 防止重复
}
return res;
}
};
二十六、求平方根
题目:实现函数 int sqrt(int x).
计算并返回x的平方根(向下取整),保留3位有效数字
核心:二分
具体核心:
class Solution {
public:
int sqrt(int x) {
// write code here
// 需要考虑溢出
if (x <= 0) return 0;
double left = 1, right = x;
while (left < right) {
double middle = (left + right) / 2;
if (middle * middle <= x && (middle + 0.001) * (middle +0.001) > x) return middle;
if (middle * middle > x) right = middle;
else left = middle;
}
return left;
}
};
二十七、找转动数组位置
题目:给出一个转动过的有序数组,你事先不知道该数组转动了多少
(例如,0 1 2 4 5 6 7可能变为4 5 6 7 0 1 2).
核心:二分找到断崖的地方,即突然减小的地方
具体核心:
class Solution {
public:
int search(int* A, int n, int target) {
// write code here
int Left=0,Right=n-1,mid;
while( Left<=Right )
{
mid= Left + (Right-Left)/2;
if( A[mid]==target )
{
return mid;
}
//左边的有序区间
if( A[mid]>=A[Left] )
{
if( A[Left]<=target && target二十八、合并k个有序链表(难题,不看)
合并k个已排序的链表并将其作为一个已排序的链表返回。分析并描述其复杂度。
核心:分治
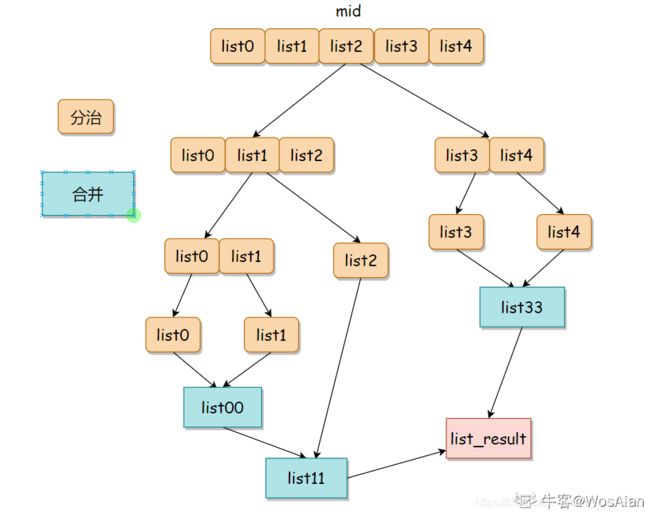
具体核心:
public class Solution {
public ListNode mergeKLists(ArrayList lists) {
return merge(lists,0,lists.size()-1);
}
public ListNode merge(ArrayList lists, int l, int r){
// 左右相等说明不能再分
if(l == r)
return lists.get(l);
if(l > r){
return null;
}
int mid = l + (r-l)/2;
return mergeTwoList(merge(lists,l,mid),merge(lists,mid+1,r));
}
//合并两个有序链表
public ListNode mergeTwoList(ListNode node1, ListNode node2){
ListNode node = new ListNode(-1);
ListNode tmp = node;
while(node1!=null && node2!=null){
if(node1.val <= node2.val){
tmp.next = node1;
node1 = node1.next;
}else{
tmp.next = node2;
node2 = node2.next;
}
tmp = tmp.next;
}
tmp.next = node1!=null?node1:node2;
return node.next;
}
}
字符串全排列
class Solution {
public:
void perm(int pos, string s, set &ret) {
if (pos+1 == s.length()) {
ret.insert(s);
return;
}
// for循环和swap的含义:对于“ABC”,
// 第一次'A' 与 'A'交换,字符串为"ABC", pos为0, 相当于固定'A'
// 第二次'A' 与 'B'交换,字符串为"BAC", pos为0, 相当于固定'B'
// 第三次'A' 与 'C'交换,字符串为"CBA", pos为0, 相当于固定'C'
for (int i = pos; i < s.length(); ++i) {
swap(s[pos], s[i]);
perm(pos+1, s, ret);
swap(s[pos], s[i]);
// 回溯的原因:比如第二次交换后是"BAC",需要回溯到"ABC"
// 然后进行第三次交换,才能得到"CBA"
}
}
vector Permutation(string s) {
if (s.empty()) return {};
set ret;
perm(0, s, ret);
return vector({ret.begin(), ret.end()});
}
};
二十九、容器盛水
核心:双指针
具体核心:
left_max:左边的最大值,它是从左往右遍历找到的
right_max:右边的最大值,它是从右往左遍历找到的
left:从左往右处理的当前下标
right:从右往左处理的当前下标
定理一:在某个位置i处,它能存的水,取决于它左右两边的最大值中较小的一个。
定理二:当我们从左往右处理到left下标时,左边的最大值left_max对它而言是可信的,但right_max对它而言是不可信的。(见下图,由于中间状况未知,对于left下标而言,right_max未必就是它右边最大的值)

定理三:当我们从右往左处理到right下标时,右边的最大值right_max对它而言是可信的,但left_max对它而言是不可信的。 核心:广度优先遍历,找到每层的最后一个节点输出 核心:深度优先搜索 核心:回文串是对称的 核心:递归 核心:如果两个数不相等,就消去这两个数,最坏情况下,每次消去一个众数和一个非众数,那么如果存在众数,最后留下的数肯定是众数。 核心:堆 核心:俩个栈,因为需要先进后出,符合栈的特点 核心:由前序遍历知道父节点,由中序遍历结合父节点知道左右节点 题目:给定一个 n * m 的矩阵 a,从左上角开始每次只能向右或者向下走,最后到达右下角的位置,路径上所有的数字累加起来就是路径和,输出所有的路径中最小的路径和。 代码: vector 模拟环 核心:堆 题目:给定一个十进制数M,以及需要转换的进制数N。将十进制数M转化为N进制数 核心:二叉树深度优先遍历 核心:二分查找 核心:求和相减 核心:奇数一个链表,偶数一个链表,然后相连即可 在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。 核心:单调栈,栈中存放的数字有序, 题目: 核心:只可能是Y形交叉,因为交叉点的next直邮一个,只可以存储一个地址。双指针。 核心: 核心:DFS + 回溯 对每一部分的整数的处理方式都是一样的,先取一位数,然后添加到临时要划分的ip字符串中,继续递归进行后面整数的划分,递归的过程中,如果划分出四个整数同时字符串又使用完毕,则组成了一种ip,否则就不是,直接返回。 题目: 题目:给出一组可能包含重复项的数字,返回该组数字的所有排列。 题目: 核心:左右两边向中间寻找 核心:构建递归式子 2.动态规划 通过研究以上递归函数发现, P(N, K)过程依赖于P(0…N-1, K-1) 和 P(0…N-1, K)。所以,若把所有的递归的返回值看作是一个二维数组,可以用动态规划的方法优化递归过程。从而减少计算量。 核心具体:将二叉树左边全部都放入栈,然后pop,k–,k==0,则直接返回,如果 题目:编号为 1到 n的 n个人围成一圈。从编号为 1 的人开始报数,报到 m 的人离开。 2.链表 核心:双指针 题目:输入一个整数,输出该数32位二进制表示中1的个数。其中负数用补码表示。 题目:给定一个由0和1组成的2维矩阵,返回该矩阵中最大的由1组成的正方形的面积 2.状态转移方程 3.边界 核心:动态规划 核心:是偶数直接加入一个vector,奇数加入另一个然后合并空间复杂度O(N) 2.冒泡,空间O(1),时间O(N) 核心:递归 核心:动态规划+dfs 题目:现在有五张扑克牌,我们需要来判断一下是不是顺子。 核心:二分法 题目:一个重复字符串是由两个相同的字符串首尾拼接而成,例如abcabc便是长度为6的一个重复字符串,而abcba则不存在重复字符串。 题目:给定一个m x n大小的矩阵(m行,n列),按螺旋的顺序返回矩阵中的所有元素。
对于位置left而言,它左边最大值一定是left_max,右边最大值“大于等于”right_max,这时候,如果left_maxint trap(vector三十、二叉树的右视图
具体核心:使用queue.size()计算每层节点数,每加入一个节点的子节点,就将该节点pop,每层使用for循环,到最后一个节点,push_back到vector中。class Solution {
public:
vector三十一、岛屿数量
具体核心:


循环走每一个格子,当是‘1’,将走过的格子标记为‘0’,递归的深度优先得标记上下左右得格子,直到与该格子相关连得全部标记为‘0’,一个岛屿找到,然后继续循环判断其他格子,每找到一个岛屿加1,找到循环结束,返回所有岛屿数目。class Solution {
private:
void dfs(vector三十二、二叉树的最大深度
public int maxDepth(TreeNode* root) {
return root==nullptr? 0 : max(maxDepth(root.->eft), maxDepth(root->right))+1 ;
}
三十三、 判断回文
具体核心:指针left从左往右,指针right从右往左,如果没比较晚len/2次就不同了就不是回文串,否则就是。class Solution {
public:
bool judge(string str) {
int len = str.length();
for(int i = 0 ; i < len/2 ;i++)
{
if(str[i]!=str[len-1-i])
return false;
}
return true;
}
};
三十四、链表排序
class Solution {
public ListNode sortList(ListNode* head) {
if (head == nullptr || head->next == nullptr)
return head;
ListNode *fast = head->next, slow *= head;
while (fast != null && fast->next != null) {
slow = slow->next;
fast = fast->next.next;
}
ListNode* tmp = slow->next;
slow->next = nullptr;
ListNode* left = sortList(head);
ListNode* right = sortList(tmp);//分割
ListNode* h = new ListNode(0);
ListNode* res = h;
while (left != nullptr&& right != nullptr) {
if (left->val < right->val) {合并
h->next = left;
left = left->next;
} else {
h->next = right;
right = right->next;
}
h = h->next;
h->next = left != nullptr ? left : right;//
return res->next;
}
}
三十五、判断是平衡二叉树
具体核心: class Solution {
public int depth(TreeNode* root){
if(root == nullptr)return 0;
int left = depth(root->left);
if(left == -1)return -1; //如果发现子树不平衡之后就没有必要进行下面的高度的求解了
int right = depth(root->right);
if(right == -1)return -1;//如果发现子树不平衡之后就没有必要进行下面的高度的求解了
if(left - right <(-1) || left - right > 1)
return -1;
else
return 1+(left > right?left:right);
}
bool IsBalanced_Solution(TreeNode* root) {
return depth(root) != -1;
}
}
三十六、数组中出现次数超过一半的数字
具体核心:用preValue记录上一次访问的值,count表明当前值出现的次数,如果下一个值和当前值相同那么count++;如果不同count–,减到0的时候就要更换新的preValue值了,因为如果存在超过数组长度一半的值,那么最后preValue一定会是该值。public class Solution {
public int MoreThanHalfNum_Solution(int [] array) {
if(array == nullptr
|| array.length == 0)return 0;
int preValue = array[0];//用来记录上一次的记录
int count = 1;//preValue出现的次数(相减之后)
for(int i = 1; i < array.length; i++){
if(array[i] == preValue)
count++;
else{
count--;
if(count == 0){
preValue = array[i];
count = 1;
}
}
}
int num = 0;//需要判断是否真的是大于1半数,这一步骤是非常有必要的,因为我们的上一次遍历只是保证如果存在超过一半的数就是preValue,但不代表preValue一定会超过一半
for(int i=0; i < array.length; i++)
if(array[i] == preValue)
num++;
return (num > array.length/2)?preValue:0;
}
}
三十七、寻找第k大
具体核心://建堆的时间复杂度近似为O(n) 调整堆的时间复杂度为O(log(n))
class Finder {
public:
int findKth(vector三十八、链表相加
具体核心:先将俩个链表的值分别存储进入俩个栈中,一个进位标志cnt,将俩个栈相加
class Solution {
public:
ListNode* addInList(ListNode* head1, ListNode* head2) {
// write code here
stack三十九、二叉树重建
具体核心:先找到根节点在中序的位置,根节点地址赋值给head指针,将左右子树的先序和中序存储在vector中,左右子树的vector作为参数递归执行函数,赋值给head的左右指针,将根节点返回。
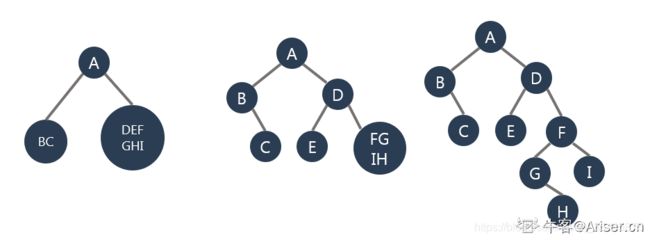
1.由先序序列第一个pre[0]在中序序列中找到根节点位置gen
2.以gen为中心遍历
0~gen左子树
子中序序列:0~gen-1,放入vin_left[]
子先序序列:1~gen放入pre_left[],+1可以看图,
因为头部有根节点
gen+1~vinlen为右子树
子中序序列:gen+1 ~ vinlen-1放入vin_right[]
子先序序列:gen+1 ~ vinlen-1放入pre_right[]
3.由先序序列pre[0]创建根节点
4.连接左子树,按照左子树子序列递归(pre_left[]和vin_left[])
5.连接右子树,按照右子树子序列递归(pre_right[]和vin_right[])
6.返回根节点class Solution {
public:
TreeNode* reConstructBinaryTree(vector pre,vector vin) {
int vinlen=vin.size();
if(vinlen==0)
return NULL;
vector pre_left, pre_right, vin_left, vin_right;
//创建根节点,根节点肯定是前序遍历的第一个数
TreeNode* head = new TreeNode(pre[0]);
//找到中序遍历根节点所在位置,存放于变量gen中
int gen=0;
for(int i=0;i四十、矩阵的最小路径和
核心:动态规划,dp里面存储的表示到当前下标为i,j节点最短的路径
具体核心:首先从第一个节点开始横竖都走一遍,然后开始将剩下的节点走一遍,剩下的节点从1,1点开始,一步一步走,目的就是将当前dp的上面和左面节点的值都求出,再走当前节点,为dp中该节点的上面和左边的节点加上当前a/[i/]/[j/]的值。最后走到dp/[/m-1]/[/n-1],返回即可。

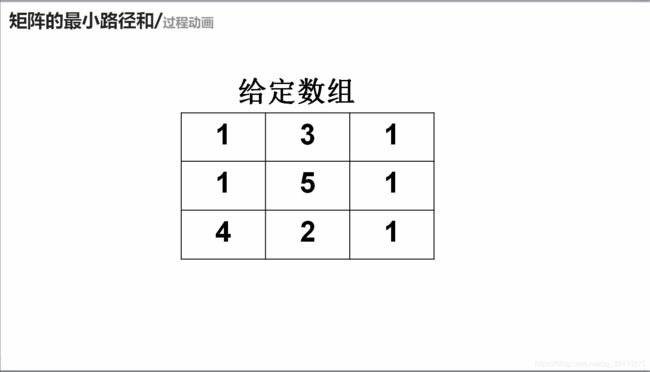
class Solution
{
public:
int minPathSum(vector四十一、最大数
#include四十二、圆圈中最后剩下的数(约瑟夫环)
class Solution {
public:
int LastRemaining_Solution(int n, int m)
{
if(n < 1 || m < 1)
return -1;
vector四十三、出现次数topk问题
具体核心:创建hash,将字符对应个数保存,创建堆,形成大根堆,将堆的前k个pop,得到结构。class Solution {
public:
struct Item {
Item(const string &str="", int n = 0):s(str),num(n){}
string s;
int num;
bool operator<(const Item &oth)const{
if(num == oth.num){
return s < oth.s;
}
return num > oth.num;
}
};
vector四十四、进制转换
核心:
具体核心:

class Solution {
public:
string solve(int M, int N) {
// write code here
if(M == 0) return "0";//如果M=0就直接返回
bool flag = false;//记录是不是负数
if(M < 0){
//如果是负数flag=true,M 取相反数
flag = true;
M = -M;
}
string res = "";//返回最终的结果
string jz = "0123456789ABCDEF";//对应进制的某一位
while(M != 0){//就对应转换为N进制的逆序样子
res += jz[M % N];
M /= N;
}
reverse(res.begin(),res.end());//逆序一下才是对应的N进制
if(flag) res.insert(0,"-");//如果是负数就在头位置插入一个-号
return res;
}
};
四十五、二叉树的所有路径和
具体核心:class Solution {
public:
// 递归遍历
void dfs(TreeNode* root, int num)
{
if(!root) return;
//if(root->left) //搜索左子树, 并将和传递下去
dfs(root->left, num*10+root->val);
//if(root->right) //搜索右子树
dfs(root->right, num*10+root->val);
num = num * 10 + root->val;
if(!root->left && !root->right){ //叶子结点,将和保存
ans += num;
}
}
int sumNumbers(TreeNode* root) {
// write code here
//很明显,可以采用递归的方式的计算
dfs(root, 0);
return ans;
}
int ans = 0;
};
四十六、矩阵元素查找
具体核心:
将每一个元素视作L左下角的数字,由矩阵性质可知L也是从小到大有序的,所以左下角数比上边所有数大,比右边所有数小。当左下角数大于x时,比左下角数更大的右边的数可以全部舍弃,于是左下角上移一格;当左下角数小于x数,比左下角数小的上边的数可以全部舍弃,于是左下角右移。最多可以舍弃n行m列(找到值的时候不舍弃直接返回了),所以时间复杂度最坏是O(n+m)class Solution {
public:
vector五十、缺失数字
具体核心:
思路:因为 0-n 个数里面只缺少一个数,所以可以直接对 0-n 求和,然后再减去a 数组的和就是答案了。class Solution {
public:
int solve(vector五十一、链表的奇偶重排
具体核心:
如果链表为空,则直接返回链表。
对于原始链表,每个节点都是奇数节点或偶数节点。头节点是奇数节点,头节点的后一个节点是偶数节点,相邻节点的奇偶性不同。因此可以将奇数节点和偶数节点分离成奇数链表和偶数链表,然后将偶数链表连接在奇数链表之后,合并后的链表即为结果链表。class Solution {
public:
ListNode* oddEvenList(ListNode* head) {
// write code here
if(head == NULL || head->next == NULL){
//如果头节点为空或者头节点的下一个节点为空直接返回
return head;
}
ListNode* odd = head;//奇链表头节点
ListNode* even = head->next;//偶链表头节点
ListNode* odd1 = odd;//进行奇链表的操作,最终成为奇链表尾节点
ListNode* even1 = even;//进行偶链表的操作,最终成为偶链表尾节点
while(odd1->next != NULL && even1->next != NULL){
/*
1->2->3->4->5
*/
odd1->next = even1->next;//奇链表的下一个节点应该等于偶数链表的下一个节点,如奇链表1下一位应该指向3
odd1 = odd1->next;//奇链表指向下一个节点
even1->next = odd1->next;//偶链表的下一个节点应该指向奇链表的下一个节点,如偶链表2下一位应该指向4
even1 = even1->next;//偶链表指向下一个节点
}
odd1->next = even;//最后将奇链表和偶链表拼接
return odd;
}
};
五十二、列表中逆序对
核心:归并
具体核心:class Solution {
public:
int mergeSort(vector五十四、优美数
具体核心:五十五、打印给定长度的所有路径
输入一颗二叉树和一个整数,打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。
核心:递归
具体核心:深度优先遍历,经过后targrt-root->val。
class TreeNode{
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x){
val = x;
}
}
class test1 {
vector五十六、 俩个链表交叉,判断交叉点
具体核心:
创建两个指针pA 和 pB,分别初始化为链表 A 和 B 的头结点。然后让它们向后逐结点遍历。
当 pA 到达链表的尾部时,将它重定位到链表 B 的头结点 (你没看错,就是链表 B); 类似的,当 pB 到达链表的尾部时,将它重定位到链表 A 的头结点。
若在某一时刻 pA 和 pB 相遇,则pA/pB 为相交结点。
想弄清楚为什么这样可行, 可以考虑以下两个链表: A={1,3,5,7,9,11} 和 B={2,4,9,11},相交于结点 9。 由于 B.length (=4) < A.length (=6),pB 比 pA 少经过 2 个结点,会先到达尾部。将 pB 重定向到 A 的头结点,pA 重定向到 B 的头结点后,pB 要比pA 多走 2 个结点。因此,它们会同时到达交点。
如果两个链表存在相交,它们末尾的结点必然相同。因此当 pA/pB 到达链表结尾时,记录下链表 A/B 对应的元素。若最后元素不相同,则两个链表不相交。class Solution {
ListNode* getIntersectionNode(ListNode* headA, ListNode headB) {
// 特判
if (headA == nullptr || headB == nullptr) {
return nullptr;
}
ListNode* head1 = headA;
ListNode* head2 = headB;
ListNode*head3,head4;
while (head1 != head2) {
if (head3 !=head4) return nullptr;//不相交
if (head1 != nullptr) {
head1 = head1->next;
} else {
head3 = head1;
head1 = headB;
}
if (head2 != nullptr) {
head2 = head2->next;
} else {
head4 = head2;
head2 = headA;
}
}
return head1;
}
}
五十七、二叉树最大路径和
class Solution {
public int res = INT_MIN;
public int maxPathSum(TreeNode root) {
getMax(root);
return res;
}
public int getMax(TreeNode root){
if(root == null) return 0;
int leftMax = max(0,getMax(root.left));
int rightMax = max(0,getMax(root.right));
//*1.--下面一行划重点--//
res = max(res,max(root.val+max(leftMax,rightMax),root.val+leftMax+rightMax));
//我们找到左子树最大值,右子树最大值加上根。这样一个值。
最后就是比较这两种情况哪个更大
//*2--这一行也很重要--//
return max(leftMax,rightMax) + root.val;//我们这个函数getMax()的作用,只是找到root节点下的最大节点和
}
}
五十八、 判断二叉树是否对称
class Solution {
public:
bool compare(TreeNode* left, TreeNode* right) {
// 首先排除空节点的情况
if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
// 排除了空节点,再排除数值不相同的情况
else if (left->val != right->val) return false;
// 此时就是:左右节点都不为空,且数值相同的情况
// 此时才做递归,做下一层的判断
bool outside = compare(left->left, right->right); // 左子树:左、 右子树:右
bool inside = compare(left->right, right->left); // 左子树:右、 右子树:左
bool isSame = outside && inside; // 左子树:中、 右子树:中 (逻辑处理)
return isSame;
}
bool isSymmetric(TreeNode* root) {
if (root == NULL) return true;
return compare(root->left, root->right);
}
};
五十九、数字转换为ip地址
具体核心:
将字符串划分成ip地址,需要注意几点:
1、ip地址由四个整数组成;
2、每个整数的范围是[0,255];
3、四个整数通过逗号分隔符连接
4、每个整数除了它本身是0的情况之外,不能以0开头
我主要采用深度优先搜索+回溯的方法解决//
// Created by jt on 2020/8/31.
//
#include 六十、重排链表
将给定的单链表L: L 0→L 1→…→L n-1→L n,
重新排序为: L 0→L n →L 1→L n-1→L 2→L n-2→…
要求使用原地算法,并且不改变节点的值
核心:先等分,后插入
具体核心:
将链表从中间断开,分成两个链表: 这里使用快慢指针方法找到中间节点,再断开。
反转第二个链表;
将第二个链表一次插入到第一个链表
链表://找到中间节点,进行断链
public class Solution {
void reorderList(ListNode* head) {
if(head == null || head.next == null || head.next.next == null)
return ;
//快慢指针,找到中间节点
ListNode fast = head;
ListNode slow = head;
while(fast != null && fast.next != null){
slow = slow.next;
fast = fast.next.next;
}
ListNode mid = slow;
ListNode start = head;
ListNode end = mid.next;
mid.next = null;//断链
//翻转end链表,处理第一个节点
ListNode pre = end;
ListNode cur = pre.next;
while(cur !=null){
if(pre == end)
pre.next = null;
ListNode next = cur.next;
cur.next = pre;
pre = cur;
cur = next;
}
end = pre;
//插入
while(start != null && end!=null){
ListNode next1 = start.next;
ListNode next2 = end.next;
start.next = end;
end.next = next1;
start = next1;
end = next2;
}
return ;
}
}
六十一、有重复数字的所有排列
核心:回溯
具体核心:public class Solution {
//用于标记是否访问过
boolean []mark;
vector六十二、最长括号子串
核心:维护一个栈,保存左括号的下标,如果遇到右括号,则弹出一个左括号,并且更新长度。注意到一个特殊情况如(())(),我们需要保存栈空时的起始节点:
具体核心:三种情况(((()),()()(),))(())。#include 六十三、回文数字
具体核心:首先计算出数字的位数
然后从数字两边向中间遍历,判断对称部位的数字是否相等class Solution {
public:
bool isPalindrome(int x) {
// write code here
if (x < 0) return false;
int digits = 0, y = x;
while(y) { ++digits; y /= 10; }
for (int i = 0; i < digits/2; ++i) {
int a = pow(10, i), b = pow(10, digits-1-i);
if (x / a % 10 != x / b % 10) return false;
}
return true;
}
};
六十四、丢棋子问题
具体核心:
设P(N,K)的返回值时N层楼时有K个棋子在最差的情况下仍的最少次数。
如果N==0,棋子在第0层肯定不会碎,所以P(0, K) = 0;
如果K==1,楼层有N层,只有1个棋子,故只能从第一次开始尝试,P(N,1)=N;
对于N>0且K>1, 我们需考虑第1个棋子是从那层开始仍的。如果第1个棋子从第i层开始仍,那么有以下两种情况:
(1) 碎了。没必要尝试第i层以上的楼层了,接下来的问题就变成了剩下i-1层楼和K-1个棋子,所以总步数为 1+P(i-1, K-1);
(2)没碎。 那么可以知道没必要尝试第i层及其以下的楼层了,接下来的问题就变成了还剩下N-i层和K个棋子,所以总步数为 1+P(N-i, K).
根据题意应该选取(1)和(2)中较差的那种情况,即 max{ P(i-1, K-1), P(N-i, K)}+1。 由于i的取值范围是 1到N, 那么步数最少的情况为, P(N, K)=min{ max{P(i-1, K-1), P(N-i, K)}(1<=i<=N) }+1。 public int solutionOne(int N, int K){
if ( N<1 || K<1 )
return 0;
return helper1(N, K);
}
private int helper1(int N, int K){
if ( N==0 ) return 0;
if ( K==1 ) return N;
int min = Integer.MAX_VALUE;
for(int i=1; i<=N; ++i){
min = Math.min(min, Math.max( helper1(i-1, K-1), helper1(N-i, K)));
}
return min+1;
}
dp[0][K] = 0, dp[N][1] = N, dp[N][K] = min( max(dp[i-1][K-1], dp[N-i][K])) + 1。 public int solutionTwo(int N, int K){
if ( N<1 || K<1 )
return 0;
if ( K == 1 ) return N;
int[][] dp = new int[N+1][K+1];
for(int i=1; i六十五、二叉搜索树的第k个节点
import java.util.Stack;
public class Solution {
TreeNode KthNode(TreeNode pRoot, int k)
{
int count = 0;
if(pRoot == null || k <= 0){
return null;
}
Stack六十六、约瑟夫环
反推过程:(当前index + m) % 上一轮剩余数字的个数
最终剩下一个人时的安全位置肯定为1,反推安全位置在人数为n时的编号
人数为1: 0+1
人数为2: (0+m) % 2+1
人数为3: ((0+m) % 2 + m) % 3+1
人数为4: (((0+m) % 2 + m) % 3 + m) % 4+1class Solution {
public:
int ysf(int n, int m) {
int last{0},ans{};
for(int i=1;i<=n;++i)
{
ans=(last+m)%i==0?i:(last+m)%i;
last=ans;
}
return ans;
// write code here
}
};
import java.util.*;
public class Solution {
public int ysf (int n, int m) {
// write code here
ListNode head=new ListNode(1);
ListNode tail=head;
for(int i=2;i<=n;i++){
tail.next=new ListNode(i);
tail=tail.next;
}
tail.next=head;
ListNode index=head;
ListNode pre=tail;
int k=0;
while(index.next!=null&&index.next!=index){
k++;
ListNode next=index.next;
if(k==m){
pre.next=pre.next.next;
k=0;
}
pre=index;
index=next;
}
return index.val;
}
}
六十七、链表中倒数第k个节点
class Solution {
public:
ListNode* FindKthToTail(ListNode* pHead, int k) {
// write code here
if(pHead==nullptr) return nullptr;
if(k<0) return nullptr;
ListNode *first=pHead;//双指针中的第一个指针
ListNode *last=pHead;
for(int i=0;i六十八、二进制中1的个数
核心代码:
现考虑二进制数:val :1101000, val-1: 1100111 那么val & (val-1) : 1100000
代码:int val; // input data
int ans = 0;
while (val != 0) {
++ans;
val = val & (val-1);
}
六十九、最大正方形
核心:动态规划
具体核心:
1.确定dp[][]数组的含义
此题的dp[i][j],代表以坐标为(i,j)的元素为右下角的正方形的边长。
dp[i][j]的值取决于dp[i-1][j],dp[i-1][j-1],dp[i][j-1]的最小值
即左方正方形的边长,左上方正方形的边长,上方正方形的边长三者的最小值。
由于状态转移方程中涉及i-1,j-1,所以i和j一定要大于0.
故dp[0][] 和 dp[][0]要首先确定。class Solution:
def solve(self , matrix ):
if not matrix: return 0
rows = len(matrix)
cols = len(matrix[0])
dp = [[0 for _ in range(cols)] for _ in range(rows)]
res = 0
# 上边界或者左边界 最大只可能有 1的矩阵
for i in range(rows):
if matrix[i][0] == '1':
dp[i][0] = 1
for j in range(cols):
if matrix[0][j] == '1':
dp[0][j] = 1
for row in range(1, rows):
for col in range(1, cols):
if matrix[row][col] == '1':
# 从左、左上、上 三个方向 判断是否 能够组成 最大矩阵
dp[row][col] = min(dp[row-1][col], dp[row][col-1], dp[row-1][col-1]) + 1
# 更新 最大值
res = max(res, dp[row][col])
return res*res
七十、字典树的实现
七十一、二叉树每层打印
class Solution {
public:
vector七十二、子数组最大乘积
具体核心:因为是连续的子数组相乘,所以最小值也可能摇身一变,成为最大值.
所以可以定义一个max_dp, min_dp,来分别遍历最大值和最小值,遇到正数保持最大最小不变,遇到负的值最大最小反转。class Solution:
def maxProduct(self , arr ):
n = len(arr)
# 初始化 最大 最小 dp数组
max_dp = [1.0]*n
min_dp = [1.0]*n
# 赋初值
min_dp[0] = arr[0]
max_dp[0] = arr[0]
total = arr[0]
for i in range(1, n):
if arr[i] > 0:
# 正*正 = 正
max_dp[i] = max(arr[i], max_dp[i-1]*arr[i])
# 负*正= 负
min_dp[i] = min(arr[i], min_dp[i-1]*arr[i])
else:
# 负*负=正
max_dp[i] = max(arr[i], min_dp[i-1]*arr[i])
# 正*负=负
min_dp[i] = min(arr[i], max_dp[i-1]*arr[i])
total = max(total, max_dp[i])
return total
七十三、调整数组使奇数位于偶数前面(且相对位置不能改变)
class Solution {
public:
vector vector七十四、合并二叉树
具体核心:分四种情况,
1.树一有节点,树二无。
2.树二右节点,树一无。
3.树一树二都有节点。
4.树一树二都无节点。
最后构造了一棵新树,返回头节点TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
// write code here
TreeNode * node = new TreeNode(0);
if(t1 == nullptr && t2== nullptr)
{
node = nullptr;
}
else if(t1 == nullptr)
{
node = t2;
}
else if(t2 == nullptr)
{
node = t1;
}
else
{
node->val = t1->val + t2->val;
node->left = mergeTrees(t1->left, t2->left);
node->right = mergeTrees(t1->right, t2->right);
}
return node;
}
七十五、矩阵最长递增路径
具体核心:
先从一个格子开始找,对比它4周的格子,有没有比它小的,如果有,比如有A,B,C三个格子都比它小,那么当前格子的最大连续递增长度就是这3个格子的最大连续递增长度中的最大值+1(有点绕,多读两遍应该就可以理解了),那么A,B,C的最大长度从哪里来呢,答案肯定是递归去找,直到找到一个比它四周都小的格子,当前格子长度就定为1,至此,整个思路就缕清了,需要用一个与matrix一样大小的数组来存放每一个格子的最大递增长度class Solution {
public int solve(int[][] matrix) {
if(matrix.length == 0){
return 0;
}
//visited有两个作用:1.判断是否访问过,2.存储当前格子的最长递增长度
int[][] visited = new int[matrix.length][matrix[0].length];
int max = 0;
for(int i=0; i七十六、有序数组转换为平衡二叉树
public class Demo3 {
public TreeNode sortedArrayToBST(int nums[]) {
if(nums==null||nums.length==0)
return null;
return sortedArrayToBST(nums,0,nums.length-1);
}
private TreeNode sortedArrayToBST(int nums[], int left, int right) {
if(right七十七、扑克牌排序
import java.util.*;
public class Solution {
public boolean isContinuous(int [] numbers) {
if(numbers.length == 0){//长度为0返回false
return false;
}
Arrays.sort(numbers);//数组排序
int count = 0;
int x = 0;
for(int i = 0;i七十八、旋转数组中的最小数
具体核心:
情况1,arr[mid] > target:4 5 6 1 2 3
arr[mid] 为 6, target为右端点 3, arr[mid] > target, 说明[first … mid] 都是 >= target 的,因为原始数组是非递减,所以可以确定答案为 [mid+1…last]区间,所以 first = mid + 1
情况2,arr[mid] < target:5 6 1 2 3 4
arr[mid] 为 1, target为右端点 4, arr[mid] < target, 说明答案肯定不在[mid+1…last],但是arr[mid] 有可能是答案,所以答案在[first, mid]区间,所以last = mid;
情况3,arr[mid] == target:
如果是 1 0 1 1 1, arr[mid] = target = 1, 显然答案在左边
如果是 1 1 1 0 1, arr[mid] = target = 1, 显然答案在右边
所以这种情况,不能确定答案在左边还是右边,那么就让last = last - 1;慢慢缩少区间,同时也不会错过答案。class Solution {
public:
int minNumberInRotateArray(vector七十九、最长重复数字
给定一个字符串,请编写一个函数,返回其最长的重复字符子串。
若不存在任何重复字符子串,则返回0。
核心:滑动窗口
具体核心:
可以将两个字符串想像成两个连续的滑动窗口,并假设这个滑动窗口最大是字符串长度的一半,通过比较两个窗口的内容是否相同,不相同的时候不断从左向右平移,完了之后,还是不相同,这时候就将窗口的大小调小一点,直到找到一个相同的,这个时候窗口的长度×2就是最大字符串的大小 public int solve (String a) {
// write code here
if (a == null || a.length() <= 1) return 0;
string chars = a
int len = chars.length();
int maxLen = chars.length() / 2;
for (int i = maxLen; i >= 1;--i){
for (int j = 0; j <= len - 2 * i;++j){
if (check(chars, j, i))
return 2 * i;
}
}
return 0;
}
public boolean check(char[] chars, int start, int len){
for (int i = start;i < start + len;++i){
if (chars[i] != chars[i +len])
return false;
}
return true;
}
八十、最近公共祖先
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
class Solution {
public:
TreeNode* dfs(TreeNode* root,int o1,int o2){
//如果当前节点为空,或者当前节点等于o1或者等于o2就返回值给父亲节点
if(root == NULL || root->val == o1 || root->val == o2) return root;
//递归遍历左子树
TreeNode *left = dfs(root->left,o1,o2);
//递归遍历右子树
TreeNode *right = dfs(root->right,o1,o2);
//如果left、right都不为空,那么代表o1、o2在root的两侧,所以root为他们的公共祖先
if(left != NULL && right != NULL) return root;
//如果left、right有一个为空,那么就返回不为空的哪一个
return left != NULL? left : right;
}
int lowestCommonAncestor(TreeNode* root, int o1, int o2) {
return dfs(root,o1,o2)->val;
}
};
八十一、螺旋矩阵
核心:按照右、下、左、上的顺序走,直到每一个方向都不可以走
具体核心:
观察一下,思路其实可以归纳为从起点(0,0)开始
先往左走,没有办法往左走了(到了边界或者是左边的格子已经走过了)就往下走,
不能往下走了以后就往右走,
不能往右走了以后就往上走,
不能往上走了以后就往左走。
直到有一个格子四个方向都不能走了,就结束循环。
所以我们设立一个visit数组,visit[i][j]表示(i,j)位置之前有没有访问过
然后建立dir数组,来表示当前的方向,如果当前方向不能走了,用(t+1)%4就可以进行以上的变换了。class Solution {
public:
vector八十二、在旋转过的有序数组中寻找目标值
int search(vector八十三、数据中的中位数
class Solution {
private:
priority_queue priority_queue