【算法】【回溯】N皇后问题【力扣-51】超详细的注释和解释手撕N皇后

【算法】【回溯】N皇后问题【力扣-51】超详细的注释和解释手撕N皇后

先赞后看好习惯 打字不容易，这都是很用心做的，希望得到支持你 大家的点赞和支持对于我来说是一种非常重要的动力 看完之后别忘记关注我哦！️️️

在本篇文章中，博主先带大家复习一下回溯算法的三部曲，然后我们按照这个模板，手撕N皇后问题。
本篇建议收藏后食用~

这边博主提供题目的传送门，食用完这篇文章后大家可以通过传送门去力扣上答题51.N皇后-力扣。

题目描述

分析

思路：
我们先来看一下皇后的约束条件：

1. 不能同行
2. 不能同列
3. 不能同斜线

很明显，皇后的位置是通过搜索出来的，每个位置进行搜索，因此，该题应使用回溯算法。
看到这里，先让我们复习一下回溯算法的模板：

1. 确定回溯函数的返回值和参数(返回类型一般为void)
2. 确定回溯函数的终止条件
3. 确定回溯搜索的遍历过程

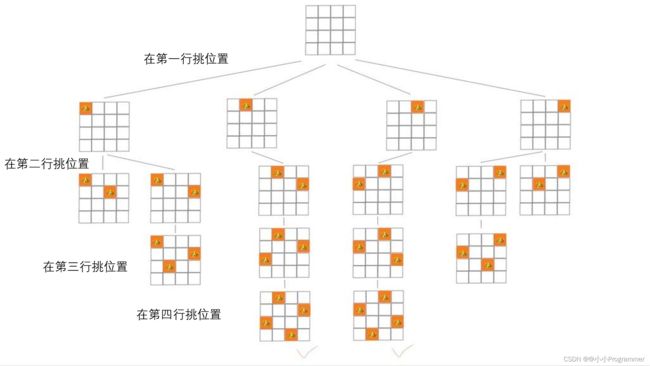
了解过回溯的伙伴都知道，回溯的搜索过程，都可以抽象成一棵树

接下来，博主用4x4棋盘将搜索过程展示给大家：

从图我们可以得知：矩阵高就是树的高度(或深度)，矩阵宽就是树的宽度。

三部曲步骤详解

一：确定递归函数
定义全局变量的二维数组来统计结果，最后用push_back()往里面加东西就可以了
n是棋盘大小，row记录现在往第几行放皇后。
其实我们可以发现，row其实就是递归的深度，为什么不需要col？，因为col是同层搜索，row是控制搜索深度的。

vector<vector<string>>ret;
void backtracking(int n,int row,vector<string>&chessboard){}

二：确定递归的终止条件
很明显，什么时候递归结束？当row到最下面那一行的时候，也就是到树的最大深度n的时候结束

if(row==n){
	ret.push_back(chessboard);
	return;
}

三：确定单层搜索的逻辑
在每次确定好row之后，我们就要开始确定col，有了行和列，我们就可以确定皇后放置的位置。

for(int col=0;col<n;col++){
	if(isValid(row,col,chessboard,n)){
		chessboard[row][col]='Q';//放置皇后
		backtracking(n,row+1,chessboard);
		chessboard[row][col]='.';//回溯，撤销皇后
	}
}

另外，我们要实现isValid()函数来判断，新皇后放置在(row,col)的位置，是否合法，合法我们才能放下去，如果不合法，进入下一次循环。

关于isValid()函数的实现，思路很简单，就是检查列，45°直线和135°直线即可。
为什么不用检查行：因为每次递归，只在每一行放一个皇后，放完就进入下一层了，所以行是肯定没问题的，不用检查。

整体代码实现

class Solution {
private:
    vector<vector<string>> ret;
    void backtracking(int n, int row, vector<string>& chessboard) {
        //这里的row就像电话号码的字母组合那道题里面的index一样，是树的深度
        //row代表现在递归到第几行了
        if (row == n) {
            ret.push_back(chessboard);
            return;
        }
        for (int col = 0; col < n; col++) {
            if (isValid(row, col, chessboard, n)) {
                //皇后下在row，col的位置后，棋盘是否合法
                chessboard[row][col] = 'Q';
                backtracking(n, row + 1, chessboard);
                chessboard[row][col] = '.';//回溯，撤销皇后
            }
        }
    }
    bool isValid(int row, int col, vector<string>& chessboard, int n) {
        int count = 0;
        //检查列--为什么不用检查行呢，因为每次递归，都只在一行放上一个，就到下一行了，所以每一行只有一个
        for (int i = 0; i < row; i++) {
            if (chessboard[i][col] == 'Q') {
                return false;
            }
        }
        //检查45°角直线是否有皇后
        for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
            if (chessboard[i][j] == 'Q')
                return false;
        }
        //检查135°直线上是否有皇后
        for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
            if (chessboard[i][j] == 'Q')
                return false;
        }
        return true;
    }
public:
    vector<vector<string>> solveNQueens(int n) {
        vector<string>chessboard(n, string(n, '.'));
        backtracking(n, 0, chessboard);
        return ret;
    }
};

尾声

看到这里，相信伙伴们对这道经典的N皇后问题已经有了一定理解了。
最后，如果你感觉在这篇文章里学到东西的话，千千万万不要忘了点赞收藏关注后再离开哦！