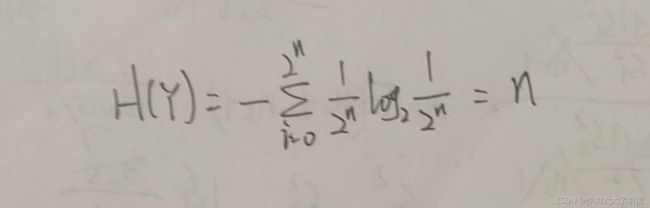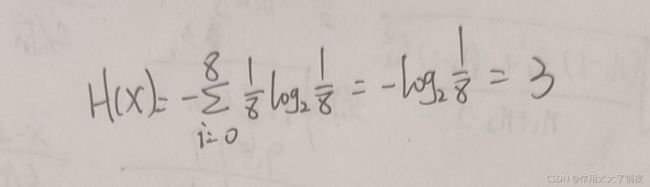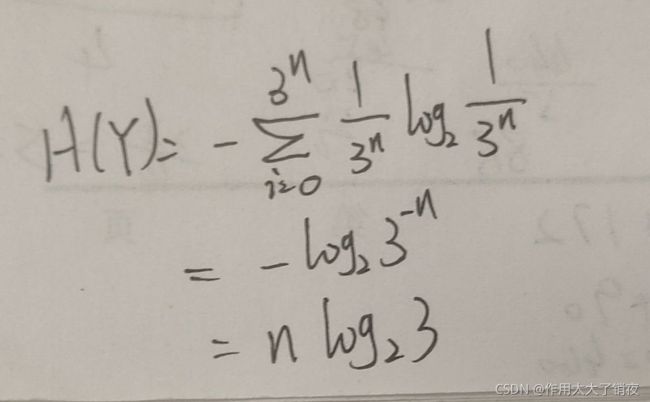2021.11.25 力扣-每日一题-可怜的小猪
目录
题目链接:力扣
本文参考:1000桶水,其中一桶有毒,猪喝毒水后会在15分钟内死去,想用一个小时找到这桶毒水,至少需要几头猪? - 知乎
题目描述:
例子1
例子2
最终推论
最终代码:
类似的问题:关于“12个球天平称3次”问题的信息学思考_DestinyAI_新浪博客
题目链接:力扣
本文参考:1000桶水,其中一桶有毒,猪喝毒水后会在15分钟内死去,想用一个小时找到这桶毒水,至少需要几头猪? - 知乎
题目描述:
有 buckets 桶液体,其中 正好 有一桶含有毒药,其余装的都是水。它们从外观看起来都一样。为了弄清楚哪只水桶含有毒药,你可以喂一些猪喝,通过观察猪是否会死进行判断。不幸的是,你只有 minutesToTest 分钟时间来确定哪桶液体是有毒的。
喂猪的规则如下:
1.选择若干活猪进行喂养
2.可以允许小猪同时饮用任意数量的桶中的水,并且该过程不需要时间。
3.小猪喝完水后,必须有 minutesToDie 分钟的冷却时间。在这段时间里,你只能观察,而不 允许继续喂猪。
4.过了 minutesToDie 分钟后,所有喝到毒药的猪都会死去,其他所有猪都会活下来。
5.重复这一过程,直到时间用完。
给你桶的数目 buckets ,minutesToDie 和 minutesToTest ,返回在规定时间内判断哪个桶有毒所需的 最小 猪数。
早上睡醒之后看到是困难题,而且样例还不给解释,直接想躺回去睡了(这个1000到底为什么能够得出5啊?)
不过搞了一天,从评论区看到题解区,再到知乎区,终于给弄懂了,如果要究其原理的话还是得回到信息论和香农定理上,不过之前貌似也没怎么学过,香农定理如下(通常情况下b取2):
看着挺复杂,但就拿知乎那篇文章的例子来说还是挺好懂的:
回到该题目上,题意可以概括为:
有x桶水,其中一桶水有毒,进行k次实验,每次可以给任意只猪喝任意桶水,问找出有毒的水最少需要使用几只猪。
例子1
例如我们先考虑有8桶水,进行1次实验的情况,那么在实验过后每只猪将会有2种状态:生或死
(1)如果从信息熵的角度来说,“8桶水中的1桶有毒”这个随机变量的信息熵为:
因为要求至少有n只猪能够找到有毒的水,所以H(Y) ≥ H(X),即n = 3.
(2)如果从信息量的角度来说,n只猪能够提供2^n个信息,也就是能够表示2^n种情况,而8桶水有8种情况,所以如果能用n只猪来表示这8桶水的话,就能够找出有毒的水,即2^n >= 8,n = 3.
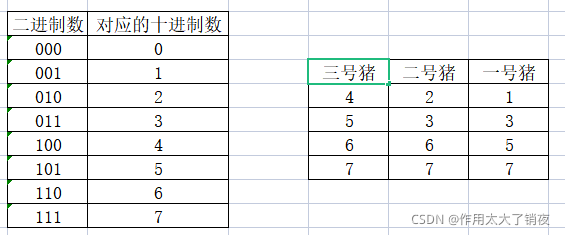
综上所述,我们可以得出至少要用n只猪,那么如何分配喝水方案呢?虽然题目不要求,但为了加深理解还是尝试分配一下:每只猪可以表示2种情况,所以使用二进制,每只猪表示一位的数字,例如下图所示:
一号猪喝的是二进制数中第一位上是1的数,二号猪喝的是二进制数中第二位上是1的数,三号猪喝的是二进制数中第三位上是1的数。
然后通过实验现象,如果一号和三号猪死亡, 二号猪活着,那么对应101,就是5号桶有毒,查上表发现一号猪和三号猪都喝了5号桶,说明5号桶确实是有毒的;当然其实不存在000,因为必定有一桶是有毒的。
例子2
如果是有8桶水,进行2次实验的情况呢?那么每只猪所代表的状态就有意思了,是3种状态:1是在第一次实验后死亡,2是在第二次实验后死亡,3是在两次实验之后都还活着。
(1)再次从信息熵的角度来看,“8桶水中的1桶有毒”这个随机变量的信息熵不变:
“n只猪实验过后的状态”这个随机变量的信息熵为:
因为要求至少有n只猪能够找到有毒的水,所以H(Y) ≥ H(X),即n = 2.
(2)如果从信息量的角度来说,n只猪能够提供3^n个信息,也就是能够表示3^n种情况,而8桶水有8种情况,所以如果能用n只猪来表示这8桶水的话,就能够找出有毒的水,即3^n >= 8,n = 2.
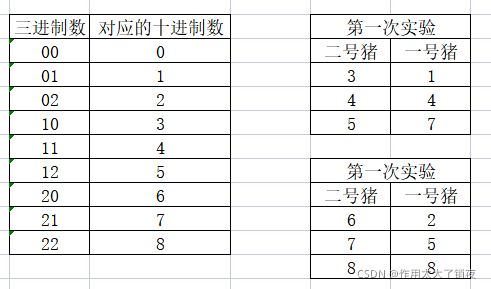
因为一只猪能够表示3种状态,所以分配喝水方案如下:
第一次实验时,一号猪喝的是三进制中第一位上是1的数,二号猪喝的是三进制中第二位上是1的数;
第一次实验时,一号猪喝的是三进制中第一位上是2的数,二号猪喝的是三进制中第二位上是2的数;
然后观察试验现象,如果一号猪在第一次实验后死亡,二号猪在第二次实验后死亡,对应的数字:
查上表可发现,第一次实验时一号猪喝了7号桶的水,第二次实验时二号猪喝了7号桶的水,说明确实是7号桶有毒。
最终推论
在有x桶水,进行k次实验的情况下,每只猪可表示 k + 1 种状态,那么推导过程如下:
最好理解的就是,n只猪可以表示 (k + 1) ^ n 种情况,只要能够表示出 x 桶水就行。
最终代码:
最后的代码其实非常简单,也就几行而已,但背后的原理才是最重要的。
class Solution {
public:
int poorPigs(int buckets, int minutesToDie, int minutesToTest) {
if (buckets == 1) return 0; //因为只有一桶水有毒,所以当只有一桶水时直接返回0
int k = minutesToTest / minutesToDie; //实验次数
int m = k + 1; //每一只猪可表达m种状态
int x = buckets; //x桶水
int n = 1; //至少需要n只猪
while (pow(m, n) < x)
{
n++;
}
return n;
}
};