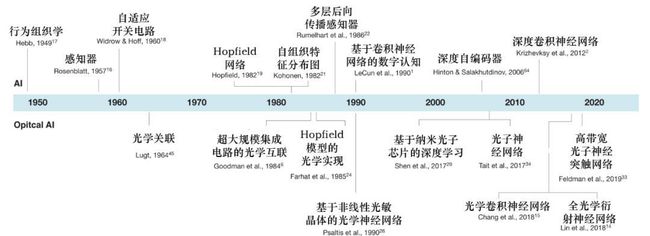
人工神经网络的发展历程,神经网络发展历程简述

神经网络的历史是什么？

沃伦·麦卡洛克和沃尔特·皮茨（1943）基于数学和一种称为阈值逻辑的算法创造了一种神经网络的计算模型。这种模型使得神经网络的研究分裂为两种不同研究思路。

一种主要关注大脑中的生物学过程，另一种主要关注神经网络在人工智能里的应用。一、赫布型学习二十世纪40年代后期，心理学家唐纳德·赫布根据神经可塑性的机制创造了一种对学习的假说，现在称作赫布型学习。

赫布型学习被认为是一种典型的非监督式学习规则，它后来的变种是长期增强作用的早期模型。从1948年开始，研究人员将这种计算模型的思想应用到B型图灵机上。

法利和韦斯利·A·克拉克（1954）首次使用计算机，当时称作计算器，在MIT模拟了一个赫布网络。纳撒尼尔·罗切斯特（1956）等人模拟了一台IBM704计算机上的抽象神经网络的行为。

弗兰克·罗森布拉特创造了感知机。这是一种模式识别算法，用简单的加减法实现了两层的计算机学习网络。罗森布拉特也用数学符号描述了基本感知机里没有的回路，例如异或回路。

这种回路一直无法被神经网络处理，直到保罗·韦伯斯(1975)创造了反向传播算法。在马文·明斯基和西摩尔·派普特（1969）发表了一项关于机器学习的研究以后，神经网络的研究停滞不前。

他们发现了神经网络的两个关键问题。第一是基本感知机无法处理异或回路。第二个重要的问题是电脑没有足够的能力来处理大型神经网络所需要的很长的计算时间。

直到计算机具有更强的计算能力之前，神经网络的研究进展缓慢。二、反向传播算法与复兴后来出现的一个关键的进展是保罗·韦伯斯发明的反向传播算法（Werbos1975）。

这个算法有效地解决了异或的问题，还有更普遍的训练多层神经网络的问题。在二十世纪80年代中期，分布式并行处理（当时称作联结主义）流行起来。

戴维·鲁姆哈特和詹姆斯·麦克里兰德的教材对于联结主义在计算机模拟神经活动中的应用提供了全面的论述。神经网络传统上被认为是大脑中的神经活动的简化模型，虽然这个模型和大脑的生理结构之间的关联存在争议。

人们不清楚人工神经网络能多大程度地反映大脑的功能。

支持向量机和其他更简单的方法（例如线性分类器）在机器学习领域的流行度逐渐超过了神经网络，但是在2000年代后期出现的深度学习重新激发了人们对神经网络的兴趣。

三、2006年之后的进展人们用CMOS创造了用于生物物理模拟和神经形态计算的计算设备。最新的研究显示了用于大型主成分分析和卷积神经网络的纳米设备具有良好的前景。

如果成功的话，这会创造出一种新的神经计算设备，因为它依赖于学习而不是编程，并且它从根本上就是模拟的而不是数字化的，虽然它的第一个实例可能是数字化的CMOS设备。

在2009到2012年之间，JürgenSchmidhuber在SwissAILabIDSIA的研究小组研发的循环神经网络和深前馈神经网络赢得了8项关于模式识别和机器学习的国际比赛。

例如，AlexGravesetal.的双向、多维的LSTM赢得了2009年ICDAR的3项关于连笔字识别的比赛，而且之前并不知道关于将要学习的3种语言的信息。

IDSIA的DanCiresan和同事根据这个方法编写的基于GPU的实现赢得了多项模式识别的比赛，包括IJCNN2011交通标志识别比赛等等。

他们的神经网络也是第一个在重要的基准测试中（例如IJCNN2012交通标志识别和NYU的扬·勒丘恩（YannLeCun）的MNIST手写数字问题）能达到或超过人类水平的人工模式识别器。

类似1980年KunihikoFukushima发明的neocognitron和视觉标准结构（由DavidH.Hubel和TorstenWiesel在初级视皮层中发现的那些简单而又复杂的细胞启发）那样有深度的、高度非线性的神经结构可以被多伦多大学杰弗里·辛顿实验室的非监督式学习方法所训练。

2012年，神经网络出现了快速的发展，主要原因在于计算技术的提高，使得很多复杂的运算变得成本低廉。以AlexNet为标志，大量的深度网络开始出现。

2014年出现了残差神经网络，该网络极大解放了神经网络的深度限制，出现了深度学习的概念。

构成典型的人工神经网络具有以下三个部分：1、结构（Architecture）结构指定了网络中的变量和它们的拓扑关系。

例如，神经网络中的变量可以是神经元连接的权重（weights）和神经元的激励值（activitiesoftheneurons）。

2、激励函数（ActivationRule）大部分神经网络模型具有一个短时间尺度的动力学规则，来定义神经元如何根据其他神经元的活动来改变自己的激励值。

一般激励函数依赖于网络中的权重（即该网络的参数）。3、学习规则（LearningRule）学习规则指定了网络中的权重如何随着时间推进而调整。这一般被看做是一种长时间尺度的动力学规则。

一般情况下，学习规则依赖于神经元的激励值。它也可能依赖于监督者提供的目标值和当前权重的值。例如，用于手写识别的一个神经网络，有一组输入神经元。输入神经元会被输入图像的数据所激发。

在激励值被加权并通过一个函数（由网络的设计者确定）后，这些神经元的激励值被传递到其他神经元。这个过程不断重复，直到输出神经元被激发。最后，输出神经元的激励值决定了识别出来的是哪个字母。

谷歌人工智能写作项目：小发猫

神经网络的发展历史

1943年，心理学家W·Mcculloch和数理逻辑学家W·Pitts在分析、总结神经元基本特性的基础上首先提出神经元的数学模型rfid。此模型沿用至今，并且直接影响着这一领域研究的进展。

因而，他们两人可称为人工神经网络研究的先驱。1945年冯·诺依曼领导的设计小组试制成功存储程序式电子计算机，标志着电子计算机时代的开始。

1948年，他在研究工作中比较了人脑结构与存储程序式计算机的根本区别，提出了以简单神经元构成的再生自动机网络结构。

但是，由于指令存储式计算机技术的发展非常迅速，迫使他放弃了神经网络研究的新途径，继续投身于指令存储式计算机技术的研究，并在此领域作出了巨大贡献。

虽然，冯·诺依曼的名字是与普通计算机联系在一起的，但他也是人工神经网络研究的先驱之一。50年代末，F·Rosenblatt设计制作了“感知机”，它是一种多层的神经网络。

这项工作首次把人工神经网络的研究从理论探讨付诸工程实践。当时，世界上许多实验室仿效制作感知机，分别应用于文字识别、声音识别、声纳信号识别以及学习记忆问题的研究。

然而，这次人工神经网络的研究高潮未能持续很久，许多人陆续放弃了这方面的研究工作，这是因为当时数字计算机的发展处于全盛时期，许多人误以为数字计算机可以解决人工智能、模式识别、专家系统等方面的一切问题，使感知机的工作得不到重视；其次，当时的电子技术工艺水平比较落后，主要的元件是电子管或晶体管，利用它们制作的神经网络体积庞大，价格昂贵，要制作在规模上与真实的神经网络相似是完全不可能的；另外，在1968年一本名为《感知机》的著作中指出线性感知机功能是有限的，它不能解决如异或这样的基本问题，而且多层网络还不能找到有效的计算方法，这些论点促使大批研究人员对于人工神经网络的前景失去信心。

60年代末期，人工神经网络的研究进入了低潮。另外，在60年代初期，Widrow提出了自适应线性元件网络，这是一种连续取值的线性加权求和阈值网络。后来，在此基础上发展了非线性多层自适应网络。

当时，这些工作虽未标出神经网络的名称，而实际上就是一种人工神经网络模型。随着人们对感知机兴趣的衰退，神经网络的研究沉寂了相当长的时间。

80年代初期，模拟与数字混合的超大规模集成电路制作技术提高到新的水平，完全付诸实用化，此外，数字计算机的发展在若干应用领域遇到困难。这一背景预示，向人工神经网络寻求出路的时机已经成熟。

美国的物理学家Hopfield于1982年和1984年在美国科学院院刊上发表了两篇关于人工神经网络研究的论文，引起了巨大的反响。人们重新认识到神经网络的威力以及付诸应用的现实性。

随即，一大批学者和研究人员围绕着Hopfield提出的方法展开了进一步的工作，形成了80年代中期以来人工神经网络的研究热潮。

人工神经网络是哪一年由谁提出来的

人工神经网络是1943年，心理学家W.S.McCulloch和数理逻辑学家W.Pitts提出来。

他们通过MP模型提出了神经元的形式化数学描述和网络结构方法，证明了单个神经元能执行逻辑功能，从而开创了人工神经网络研究的时代。1949年，心理学家提出了突触联系强度可变的设想。

60年代，人工神经网络得到了进一步发展，更完善的神经网络模型被提出，其中包括感知器和自适应线性元件等。

M.Minsky等仔细分析了以感知器为代表的神经网络系统的功能及局限后，于1969年出版了《Perceptron》一书，指出感知器不能解决高阶谓词问题。

扩展资料人工神经网络的特点和优越性，主要表现在三个方面：第一，具有自学习功能。

例如实现图像识别时，只在先把许多不同的图像样板和对应的应识别的结果输入人工神经网络，网络就会通过自学习功能，慢慢学会识别类似的图像。自学习功能对于预测有特别重要的意义。

预期未来的人工神经网络计算机将为人类提供经济预测、市场预测、效益预测，其应用前途是很远大的。第二，具有联想存储功能。用人工神经网络的反馈网络就可以实现这种联想。第三，具有高速寻找优化解的能力。

寻找一个复杂问题的优化解，往往需要很大的计算量，利用一个针对某问题而设计的反馈型人工神经网络，发挥计算机的高速运算能力，可能很快找到优化解。

有人可以介绍一下什么是"神经网络"吗?

由于神经网络是多学科交叉的产物，各个相关的学科领域对神经网络都有各自的看法，因此，关于神经网络的定义，在科学界存在许多不同的见解。

目前使用得最广泛的是T.Koholen的定义，即"神经网络是由具有适应性的简单单元组成的广泛并行互连的网络，它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。

"如果我们将人脑神经信息活动的特点与现行冯·诺依曼计算机的工作方式进行比较，就可以看出人脑具有以下鲜明特征：1.巨量并行性。

在冯·诺依曼机中，信息处理的方式是集中、串行的，即所有的程序指令都必须调到CPU中后再一条一条地执行。而人在识别一幅图像或作出一项决策时，存在于脑中的多方面的知识和经验会同时并发作用以迅速作出解答。

据研究，人脑中约有多达10^(10)～10^(11)数量级的神经元，每一个神经元具有103数量级的连接，这就提供了巨大的存储容量，在需要时能以很高的反应速度作出判断。

2.信息处理和存储单元结合在一起。在冯·诺依曼机中，存储内容和存储地址是分开的，必须先找出存储器的地址，然后才能查出所存储的内容。一旦存储器发生了硬件故障，存储器中存储的所有信息就都将受到毁坏。

而人脑神经元既有信息处理能力又有存储功能，所以它在进行回忆时不仅不用先找存储地址再调出所存内容，而且可以由一部分内容恢复全部内容。

当发生"硬件"故障（例如头部受伤）时，并不是所有存储的信息都失效，而是仅有被损坏得最严重的那部分信息丢失。3.自组织自学习功能。

冯·诺依曼机没有主动学习能力和自适应能力，它只能不折不扣地按照人们已经编制好的程序步骤来进行相应的数值计算或逻辑计算。

而人脑能够通过内部自组织、自学习的能力，不断地适应外界环境，从而可以有效地处理各种模拟的、模糊的或随机的问题。神经网络研究的主要发展过程大致可分为四个阶段：1.第一阶段是在五十年代中期之前。

西班牙解剖学家Cajal于十九世纪末创立了神经元学说，该学说认为神经元的形状呈两极，其细胞体和树突从其他神经元接受冲动，而轴索则将信号向远离细胞体的方向传递。

在他之后发明的各种染色技术和微电极技术不断提供了有关神经元的主要特征及其电学性质。

1943年，美国的心理学家W.S.McCulloch和数学家W.A.Pitts在论文《神经活动中所蕴含思想的逻辑活动》中，提出了一个非常简单的神经元模型，即M－P模型。

该模型将神经元当作一个功能逻辑器件来对待，从而开创了神经网络模型的理论研究。

1949年，心理学家D.O.Hebb写了一本题为《行为的组织》的书，在这本书中他提出了神经元之间连接强度变化的规则，即后来所谓的Hebb学习法则。

Hebb写道："当神经细胞A的轴突足够靠近细胞B并能使之兴奋时，如果A重复或持续地激发B，那么这两个细胞或其中一个细胞上必然有某种生长或代谢过程上的变化，这种变化使A激活B的效率有所增加。

"简单地说，就是如果两个神经元都处于兴奋状态，那么它们之间的突触连接强度将会得到增强。

五十年代初，生理学家Hodykin和数学家Huxley在研究神经细胞膜等效电路时，将膜上离子的迁移变化分别等效为可变的Na+电阻和K+电阻，从而建立了著名的Hodykin-Huxley方程。

这些先驱者的工作激发了许多学者从事这一领域的研究，从而为神经计算的出现打下了基础。2.第二阶段从五十年代中期到六十年代末。

1958年，F.Rosenblatt等人研制出了历史上第一个具有学习型神经网络特点的模式识别装置，即代号为MarkI的感知机（Perceptron），这一重大事件是神经网络研究进入第二阶段的标志。

对于最简单的没有中间层的感知机，Rosenblatt证明了一种学习算法的收敛性，这种学习算法通过迭代地改变连接权来使网络执行预期的计算。

稍后于Rosenblatt，B.Widrow等人创造出了一种不同类型的会学习的神经网络处理单元，即自适应线性元件Adaline，并且还为Adaline找出了一种有力的学习规则，这个规则至今仍被广泛应用。

Widrow还建立了第一家神经计算机硬件公司，并在六十年代中期实际生产商用神经计算机和神经计算机软件。

除Rosenblatt和Widrow外，在这个阶段还有许多人在神经计算的结构和实现思想方面作出了很大的贡献。例如，K.Steinbuch研究了称为学习矩阵的一种二进制联想网络结构及其硬件实现。

N.Nilsson于1965年出版的《机器学习》一书对这一时期的活动作了总结。3.第三阶段从六十年代末到八十年代初。

第三阶段开始的标志是1969年M.Minsky和S.Papert所著的《感知机》一书的出版。

该书对单层神经网络进行了深入分析，并且从数学上证明了这种网络功能有限，甚至不能解决象"异或"这样的简单逻辑运算问题。同时，他们还发现有许多模式是不能用单层网络训练的，而多层网络是否可行还很值得怀疑。

由于M.Minsky在人工智能领域中的巨大威望，他在论著中作出的悲观结论给当时神经网络沿感知机方向的研究泼了一盆冷水。

在《感知机》一书出版后，美国联邦基金有15年之久没有资助神经网络方面的研究工作，前苏联也取消了几项有前途的研究计划。

但是，即使在这个低潮期里，仍有一些研究者继续从事神经网络的研究工作，如美国波士顿大学的S.Grossberg、芬兰赫尔辛基技术大学的T.Kohonen以及日本东京大学的甘利俊一等人。

他们坚持不懈的工作为神经网络研究的复兴开辟了道路。4.第四阶段从八十年代初至今。

1982年，美国加州理工学院的生物物理学家J.J.Hopfield采用全互连型神经网络模型，利用所定义的计算能量函数，成功地求解了计算复杂度为NP完全型的旅行商问题（TravellingSalesmanProblem，简称TSP）。

这项突破性进展标志着神经网络方面的研究进入了第四阶段，也是蓬勃发展的阶段。Hopfield模型提出后，许多研究者力图扩展该模型，使之更接近人脑的功能特性。

1983年，T.Sejnowski和G.Hinton提出了"隐单元"的概念，并且研制出了Boltzmann机。

日本的福岛邦房在Rosenblatt的感知机的基础上，增加隐层单元，构造出了可以实现联想学习的"认知机"。Kohonen应用3000个阈器件构造神经网络实现了二维网络的联想式学习功能。

1986年，D.Rumelhart和J.McClelland出版了具有轰动性的著作《并行分布处理-认知微结构的探索》，该书的问世宣告神经网络的研究进入了高潮。

1987年，首届国际神经网络大会在圣地亚哥召开，国际神经网络联合会（INNS）成立。

随后INNS创办了刊物《JournalNeuralNetworks》，其他专业杂志如《NeuralComputation》，《IEEETransactionsonNeuralNetworks》，《InternationalJournalofNeuralSystems》等也纷纷问世。

世界上许多著名大学相继宣布成立神经计算研究所并制订有关教育计划，许多国家也陆续成立了神经网络学会，并召开了多种地区性、国际性会议，优秀论著、重大成果不断涌现。

今天，在经过多年的准备与探索之后，神经网络的研究工作已进入了决定性的阶段。日本、美国及西欧各国均制订了有关的研究规划。日本制订了一个"人类前沿科学计划"。

这项计划为期15－20年，仅初期投资就超过了1万亿日元。在该计划中，神经网络和脑功能的研究占有重要地位，因为所谓"人类前沿科学"首先指的就是有关人类大脑以及通过借鉴人脑而研制新一代计算机的科学领域。

在美国，神经网络的研究得到了军方的强有力的支持。美国国防部投资4亿美元，由国防部高级研究计划局（DAPRA）制订了一个8年研究计划，并成立了相应的组织和指导委员会。

同时，海军研究办公室（ONR）、空军科研办公室（AFOSR）等也纷纷投入巨额资金进行神经网络的研究。DARPA认为神经网络"看来是解决机器智能的唯一希望"，并认为"这是一项比原子弹工程更重要的技术"。

美国国家科学基金会（NSF）、国家航空航天局（NASA）等政府机构对神经网络的发展也都非常重视，它们以不同的形式支持了众多的研究课题。欧共体也制订了相应的研究计划。

在其ESPRIT计划中，就有一个项目是"神经网络在欧洲工业中的应用"，除了英、德两国的原子能机构外，还有多个欧洲大公司卷进这个研究项目，如英国航天航空公司、德国西门子公司等。

此外，西欧一些国家还有自己的研究计划，如德国从1988年就开始进行一个叫作"神经信息论"的研究计划。我国从1986年开始，先后召开了多次非正式的神经网络研讨会。

1990年12月，由中国计算机学会、电子学会、人工智能学会、自动化学会、通信学会、物理学会、生物物理学会和心理学会等八个学会联合在北京召开了"中国神经网络首届学术会议"，从而开创了我国神经网络研究的新纪元。

人工神经网络，人工神经网络是什么意思

。

一、人工神经网络的概念人工神经网络（ArtificialNeuralNetwork，ANN）简称神经网络(NN)，是基于生物学中神经网络的基本原理，在理解和抽象了人脑结构和外界刺激响应机制后，以网络拓扑知识为理论基础，模拟人脑的神经系统对复杂信息的处理机制的一种数学模型。

该模型以并行分布的处理能力、高容错性、智能化和自学习等能力为特征，将信息的加工和存储结合在一起，以其独特的知识表示方式和智能化的自适应学习能力，引起各学科领域的关注。

它实际上是一个有大量简单元件相互连接而成的复杂网络，具有高度的非线性，能够进行复杂的逻辑操作和非线性关系实现的系统。神经网络是一种运算模型，由大量的节点（或称神经元）之间相互联接构成。

每个节点代表一种特定的输出函数，称为激活函数（activationfunction）。

每两个节点间的连接都代表一个对于通过该连接信号的加权值，称之为权重（weight），神经网络就是通过这种方式来模拟人类的记忆。网络的输出则取决于网络的结构、网络的连接方式、权重和激活函数。

而网络自身通常都是对自然界某种算法或者函数的逼近，也可能是对一种逻辑策略的表达。神经网络的构筑理念是受到生物的神经网络运作启发而产生的。

人工神经网络则是把对生物神经网络的认识与数学统计模型相结合，借助数学统计工具来实现。

另一方面在人工智能学的人工感知领域，我们通过数学统计学的方法，使神经网络能够具备类似于人的决定能力和简单的判断能力，这种方法是对传统逻辑学演算的进一步延伸。

人工神经网络中，神经元处理单元可表示不同的对象，例如特征、字母、概念，或者一些有意义的抽象模式。网络中处理单元的类型分为三类：输入单元、输出单元和隐单元。

输入单元接受外部世界的信号与数据；输出单元实现系统处理结果的输出；隐单元是处在输入和输出单元之间，不能由系统外部观察的单元。

神经元间的连接权值反映了单元间的连接强度，信息的表示和处理体现在网络处理单元的连接关系中。

人工神经网络是一种非程序化、适应性、大脑风格的信息处理，其本质是通过网络的变换和动力学行为得到一种并行分布式的信息处理功能，并在不同程度和层次上模仿人脑神经系统的信息处理功能。

神经网络，是一种应用类似于大脑神经突触连接结构进行信息处理的数学模型，它是在人类对自身大脑组织结合和思维机制的认识理解基础之上模拟出来的，它是根植于神经科学、数学、思维科学、人工智能、统计学、物理学、计算机科学以及工程科学的一门技术。

二、人工神经网络的发展神经网络的发展有悠久的历史。其发展过程大致可以概括为如下4个阶段。

1.第一阶段----启蒙时期(1)、M-P神经网络模型：20世纪40年代，人们就开始了对神经网络的研究。

1943年，美国心理学家麦克洛奇（Mcculloch）和数学家皮兹（Pitts）提出了M-P模型，此模型比较简单，但是意义重大。

在模型中，通过把神经元看作个功能逻辑器件来实现算法，从此开创了神经网络模型的理论研究。

(2)、Hebb规则：1949年，心理学家赫布（Hebb）出版了《TheOrganizationofBehavior》（行为组织学），他在书中提出了突触连接强度可变的假设。

这个假设认为学习过程最终发生在神经元之间的突触部位，突触的连接强度随之突触前后神经元的活动而变化。这一假设发展成为后来神经网络中非常著名的Hebb规则。

这一法则告诉人们，神经元之间突触的联系强度是可变的，这种可变性是学习和记忆的基础。Hebb法则为构造有学习功能的神经网络模型奠定了基础。

(3)、感知器模型：1957年，罗森勃拉特（Rosenblatt）以M-P模型为基础，提出了感知器（Perceptron）模型。

感知器模型具有现代神经网络的基本原则，并且它的结构非常符合神经生理学。

这是一个具有连续可调权值矢量的MP神经网络模型，经过训练可以达到对一定的输入矢量模式进行分类和识别的目的，它虽然比较简单，却是第一个真正意义上的神经网络。

Rosenblatt证明了两层感知器能够对输入进行分类，他还提出了带隐层处理元件的三层感知器这一重要的研究方向。

Rosenblatt的神经网络模型包含了一些现代神经计算机的基本原理，从而形成神经网络方法和技术的重大突破。

(4)、ADALINE网络模型：1959年，美国著名工程师威德罗（B.Widrow）和霍夫（M.Hoff）等人提出了自适应线性元件(Adaptivelinearelement，简称Adaline)和Widrow-Hoff学习规则（又称最小均方差算法或称δ规则）的神经网络训练方法，并将其应用于实际工程，成为第一个用于解决实际问题的人工神经网络，促进了神经网络的研究应用和发展。

ADALINE网络模型是一种连续取值的自适应线性神经元网络模型，可以用于自适应系统。

2.第二阶段----低潮时期人工智能的创始人之一Minsky和Papert对以感知器为代表的网络系统的功能及局限性从数学上做了深入研究，于1969年发表了轰动一时《Perceptrons》一书，指出简单的线性感知器的功能是有限的，它无法解决线性不可分的两类样本的分类问题，如简单的线性感知器不可能实现“异或”的逻辑关系等。

这一论断给当时人工神经元网络的研究带来沉重的打击。开始了神经网络发展史上长达10年的低潮期。

(1)、自组织神经网络SOM模型：1972年，芬兰的KohonenT.教授，提出了自组织神经网络SOM(Self-Organizingfeaturemap)。

后来的神经网络主要是根据KohonenT.的工作来实现的。SOM网络是一类无导师学习网络，主要用于模式识别﹑语音识别及分类问题。

它采用一种“胜者为王”的竞争学习算法，与先前提出的感知器有很大的不同，同时它的学习训练方式是无指导训练，是一种自组织网络。

这种学习训练方式往往是在不知道有哪些分类类型存在时，用作提取分类信息的一种训练。

(2)、自适应共振理论ART：1976年，美国Grossberg教授提出了著名的自适应共振理论ART(AdaptiveResonanceTheory)，其学习过程具有自组织和自稳定的特征。

3.第三阶段----复兴时期(1)、Hopfield模型：1982年，美国物理学家霍普菲尔德（Hopfield）提出了一种离散神经网络，即离散Hopfield网络，从而有力地推动了神经网络的研究。

在网络中，它首次将李雅普诺夫（Lyapunov）函数引入其中，后来的研究学者也将Lyapunov函数称为能量函数。证明了网络的稳定性。

1984年，Hopfield又提出了一种连续神经网络，将网络中神经元的激活函数由离散型改为连续型。

1985年，Hopfield和Tank利用Hopfield神经网络解决了著名的旅行推销商问题（TravellingSalesmanProblem）。Hopfield神经网络是一组非线性微分方程。

Hopfield的模型不仅对人工神经网络信息存储和提取功能进行了非线性数学概括，提出了动力方程和学习方程，还对网络算法提供了重要公式和参数，使人工神经网络的构造和学习有了理论指导，在Hopfield模型的影响下，大量学者又激发起研究神经网络的热情，积极投身于这一学术领域中。

因为Hopfield神经网络在众多方面具有巨大潜力，所以人们对神经网络的研究十分地重视，更多的人开始了研究神经网络，极大地推动了神经网络的发展。

(2)、Boltzmann机模型：1983年，Kirkpatrick等人认识到模拟退火算法可用于NP完全组合优化问题的求解，这种模拟高温物体退火过程来找寻全局最优解的方法最早由Metropli等人1953年提出的。

1984年，Hinton与年轻学者Sejnowski等合作提出了大规模并行网络学习机，并明确提出隐单元的概念，这种学习机后来被称为Boltzmann机。

Hinton和Sejnowsky利用统计物理学的感念和方法，首次提出的多层网络的学习算法，称为Boltzmann机模型。

(3)、BP神经网络模型：1986年，儒默哈特（melhart）等人在多层神经网络模型的基础上，提出了多层神经网络权值修正的反向传播学习算法----BP算法（ErrorBack-Propagation），解决了多层前向神经网络的学习问题，证明了多层神经网络具有很强的学习能力，它可以完成许多学习任务，解决许多实际问题。

(4)、并行分布处理理论：1986年，由Rumelhart和McCkekkand主编的《ParallelDistributedProcessing：ExplorationintheMicrostructuresofCognition》，该书中，他们建立了并行分布处理理论，主要致力于认知的微观研究，同时对具有非线性连续转移函数的多层前馈网络的误差反向传播算法即BP算法进行了详尽的分析，解决了长期以来没有权值调整有效算法的难题。

可以求解感知机所不能解决的问题，回答了《Perceptrons》一书中关于神经网络局限性的问题，从实践上证实了人工神经网络有很强的运算能力。

(5)、细胞神经网络模型：1988年，Chua和Yang提出了细胞神经网络（CNN）模型，它是一个细胞自动机特性的大规模非线性计算机仿真系统。

Kosko建立了双向联想存储模型（BAM），它具有非监督学习能力。(6)、Darwinism模型：Edelman提出的Darwinism模型在90年代初产生了很大的影响，他建立了一种神经网络系统理论。

(7)、1988年，Linsker对感知机网络提出了新的自组织理论，并在Shanon信息论的基础上形成了最大互信息理论，从而点燃了基于NN的信息应用理论的光芒。

(8)、1988年，Broomhead和Lowe用径向基函数(Radialbasisfunction,RBF)提出分层网络的设计方法，从而将NN的设计与数值分析和线性适应滤波相挂钩。

(9)、1991年，Haken把协同引入神经网络，在他的理论框架中，他认为，认知过程是自发的，并断言模式识别过程即是模式形成过程。

(10)、1994年，廖晓昕关于细胞神经网络的数学理论与基础的提出，带来了这个领域新的进展。

通过拓广神经网络的激活函数类，给出了更一般的时滞细胞神经网络(DCNN)、Hopfield神经网络（HNN）、双向联想记忆网络（BAM）模型。

(11)、90年代初，Vapnik等提出了支持向量机(Supportvectormachines,SVM)和VC(Vapnik-Chervonenkis)维数的概念。

经过多年的发展，已有上百种的神经网络模型被提出。

人工智能的起源是什么？

人工智能（ArtificialIntelligence）,英文缩写为AI,是一门由计算机科学、控制论、信息论、语言学、神经生理学、心理学、数学、哲学等多种学科相互渗透而发展起来的综合性新学科。

自问世以来AI经过波波折折，但终于作为一门边缘新学科得到世界的承认并且日益引起人们的兴趣和关注。

不仅许多其他学科开始引入或借用AI技术，而且AI中的专家系统、自然语言处理和图象识别已成为新兴的知识产业的三大突破口。

人工智能的思想萌芽可以追溯到十七世纪的巴斯卡和莱布尼茨，他们较早萌生了有智能的机器的想法。十九世纪，英国数学家布尔和德o摩尔根提出了“思维定律“，这些可谓是人工智能的开端。

十九世纪二十年代，英国科学家巴贝奇设计了第一架“计算机器“，它被认为是计算机硬件，也是人工智能硬件的前身。电子计算机的问世，使人工智能的研究真正成为可能。

作为一门学科，人工智能于1956年问世，是由“人工智能之父“McCarthy及一批数学家、信息学家、心理学家、神经生理学家、计算机科学家在Dartmouth大学召开的会议上，首次提出。

对人工智能的研究，由于研究角度的不同，形成了不同的研究学派。这就是：符号主义学派、连接主义学派和行为主义学派。

传统人工智能是符号主义，它以Newell和Simon提出的物理符号系统假设为基础。

物理符号系统是由一组符号实体组成，它们都是物理模式，可在符号结构的实体中作为组成成分出现，可通过各种操作生成其它符号结构。物理符号系统假设认为：物理符号系统是智能行为的充分和必要条件。

主要工作是“通用问题求解程序“（GeneralProblemSolver,GPS）：通过抽象，将一个现实系统变成一个符号系统，基于此符号系统，使用动态搜索方法求解问题。

连接主义学派是从人的大脑神经系统结构出发，研究非程序的、适应性的、大脑风格的信息处理的本质和能力，研究大量简单的神经元的集团信息处理能力及其动态行为。人们也称之为神经计算。

研究重点是侧重于模拟和实现人的认识过程中的感觉、知觉过程、形象思维、分布式记忆和自学习、自组织过程。行为主义学派是从行为心理学出发，认为智能只是在与环境的交互作用中表现出来。

人工智能的研究经历了以下几个阶段：第一阶段：50年代人工智能的兴起和冷落人工智能概念首次提出后，相继出现了一批显著的成果，如机器定理证明、跳棋程序、通用问题s求解程序、LISP表处理语言等。

但由于消解法推理能力的有限，以及机器翻译等的失败，使人工智能走入了低谷。这一阶段的特点是：重视问题求解的方法，忽视知识重要性。

第二阶段：60年代末到70年代，专家系统出现，使人工智能研究出现新高潮DENDRAL化学质谱分析系统、MYCIN疾病诊断和治疗系统、PROSPECTIOR探矿系统、Hearsay-II语音理解系统等专家系统的研究和开发，将人工智能引向了实用化。

并且，1969年成立了国际人工智能联合会议（InternationalJointConferencesonArtificialIntelligence即IJCAI）。

第三阶段：80年代，随着第五代计算机的研制，人工智能得到了很大发展日本1982年开始了“第五代计算机研制计划“，即“知识信息处理计算机系统KIPS“，其目的是使逻辑推理达到数值运算那么快。

虽然此计划最终失败，但它的开展形成了一股研究人工智能的热潮。第四阶段：80年代末，神经网络飞速发展1987年，美国召开第一次神经网络国际会议，宣告了这一新学科的诞生。

此后，各国在神经网络方面的投资逐渐增加，神经网络迅速发展起来。

第五阶段：90年代，人工智能出现新的研究高潮由于网络技术特别是国际互连网的技术发展，人工智能开始由单个智能主体研究转向基于网络环境下的分布式人工智能研究。

不仅研究基于同一目标的分布式问题求解，而且研究多个智能主体的多目标问题求解，将人工智能更面向实用。另外，由于Hopfield多层神经网络模型的提出，使人工神经网络研究与应用出现了欣欣向荣的景象。

人工智能已深入到社会生活的各个领域。

IBM公司“深蓝“电脑击败了人类的世界国际象棋冠军，美国制定了以多Agent系统应用为重要研究内容的信息高速公路计划，基于Agent技术的Softbot(软机器人)在软件领域和网络搜索引擎中得到了充分应用，同时，美国Sandia实验室建立了国际上最庞大的“虚拟现实“实验室，拟通过数据头盔和数据手套实现更友好的人机交互，建立更好的智能用户接口。

图像处理和图像识别，声音处理和声音识别取得了较好的发展，IBM公司推出了ViaVoice声音识别软件，以使声音作为重要的信息输入媒体。国际各大计算机公司又开始将“人工智能“作为其研究内容。

人们普遍认为，计算机将会向网络化、智能化、并行化方向发展。二十一世纪的信息技术领域将会以智能信息处理为中心。

目前人工智能主要研究内容是：分布式人工智能与多智能主体系统、人工思维模型、知识系统（包括专家系统、知识库系统和智能决策系统）、知识发现与数据挖掘（从大量的、不完全的、模糊的、有噪声的数据中挖掘出对我们有用的知识）、遗传与演化计算（通过对生物遗传与进化理论的模拟，揭示出人的智能进化规律）、人工生命（通过构造简单的人工生命系统（如：机器虫）并观察其行为，探讨初级智能的奥秘）、人工智能应用（如：模糊控制、智能大厦、智能人机接口、智能机器人等）等等。

人工智能研究与应用虽取得了不少成果，但离全面推广应用还有很大的距离，还有许多问题有待解决，且需要多学科的研究专家共同合作。

未来人工智能的研究方向主要有：人工智能理论、机器学习模型和理论、不精确知识表示及其推理、常识知识及其推理、人工思维模型、智能人机接口、多智能主体系统、知识发现与知识获取、人工智能应用基础等。

Hopfield神经网络

。

Hopfield神经网络(HopfieldNeuralNetwork，简称HNN)，是美国加州理工学院物理学家Hopfield教授1982年提出的一种反馈型神经网络，信号不但能向前，还能向后传递(输出信号又反馈回来变成输入信号。

而前面所介绍的BP网络是一种前馈网络，信号只能向前传递)。他在Hopfield神经网络中引入了“能量函数”概念，使网络的运行稳定性的判断有了可靠依据。

Hopfield神经网络的权值不是经过反复学习获得的，而是按照一定规则计算出来的，一经确定就不再改变，而Hopfield神经网络的状态(输入、输出信号)会在运行过程中不断更新，网络演变到稳态时各神经元的状态便是问题的解。

1985年，Hopfield和Tank研制了电子线路来模拟Hopfield网络，较好地解决了优化组合问题中著名的TSP(旅行商)问题，找到了最佳解的近似解，为神经网络的复兴建立了不可磨灭的功劳。

对于地球物理反演这种最优化问题，可以很方便地用Hopfield网络来实现。

反演的目标函数等于Hopfield网络的“能量函数”，网络的状态(输入、输出信号)就是模型的参数，网络演变到稳态时各神经元的输入输出值便是反演问题的解。

Hopfield神经网络分为离散型和连续型两种网络模型，分别记为DHNN(DiscreteHopfieldNeuralNetwork)和CHNN(ContinuesHopfieldNeuralNetwork)。

在前馈型网络中无论是离散的还是连续的，一般均不考虑输入与输出之间在时间上的滞后性，而只表达两者之间的映射关系。

但在连续Hopfield神经网络中，考虑了输出与输入之间的延迟因素，因此需要用微分方程或差分方程来描述网络的动态数学模型。

8.5.4.1离散Hopfield神经网络离散Hopfield神经网络的拓扑结构如图8.12所示。这是一种单层全反馈网络，共有n个神经元。

图8.12的特点是任意一个神经元的输出xi只能是0或1，均通过连接权wij反馈至所有神经元j作为它的输入xj。

也就是说，每个神经元都通过连接权接收所有其他神经元输出反馈的信息，这样每一个神经元的输出都受其他所有神经元输出的控制，从而每个神经元的输出相互制约。每个神经元均设一个阀值Ti，以反映对输入噪声的控制。

图8.12离散Hopfield神经网络的拓扑结构[8]8.5.4.1.1网络的状态离散Hopfield神经网络任意一个神经元的输出xj称为网络的状态，它只能是0或1。

变化规律由下式规定:xj=f(netj)j=1，2，…，n(8.33)f()为转移函数，离散Hopfield神经网络的转移函数常用符号函数表示:地球物理反演教程其中netj为净输入:地球物理反演教程对离散Hopfield神经网络，一般有wij=0，wij=wji(8.36)这说明神经元没有自反馈，两个神经元的相互控制权值相同。

离散Hopfield神经网络稳定时，每个神经元的状态都不再改变。

此时的稳定状态就是网络的输出，记为地球物理反演教程8.5.4.1.2网络的异步工作方式它是一种串行方式，网络运行时每次只改变一个神经元的状态，其他神经元的状态保持不变。

8.5.4.1.3网络的同步工作方式它是一种并行同步工作方式，所有神经元同时调整状态。8.5.4.1.4网络的吸引子网络达到稳定状态时的输出X，称为网络的吸引子。

8.5.4.1.5网络的能量函数网络的能量函数定义为地球物理反演教程以上是矩阵形式，考虑无自反馈的具体展开形式为地球物理反演教程当网络收敛到稳定状态时，有ΔE(t)=E(t+1)-E(t)=0(8.40)或者说:地球物理反演教程理论证明了如下两个定理[8]:定理1.对于DHNN，若按异步方式调整网络状态，且连接权矩阵W为对称阵，则对任意初始状态，网络都能最终收敛到一个吸引子。

定理2.对于DHNN，若按同步方式调整网络状态，且连接权矩阵W为非负定对称阵，则对任意初始状态，网络都能最终收敛到一个吸引子。

8.5.4.1.6利用离散Hopfield神经网络进行反演在地球物理线性反演中，设有如下目标函数:地球物理反演教程对比式(8.38)和式(8.42)发现它们在形式上有很多相似之处。

王家映的《地球物理反演理论》一书中，直接用式(8.42)和式(8.38)类比，公式显得复杂。

本书设立一个新的目标函数ϕ，公式将会变得简洁得多:地球物理反演教程再对比式(8.38)和式(8.43)，发现它们完全一样，只要设:X(t)=m，W=GTG，T=GTd(8.44)注意:式(8.43)的目标函数ϕ的极大值解就是原来目标函数φ极小值的解，它们是同解的。

如果待反演的模型参数是离散的0或1值，那么可以直接应用离散Hopfield神经网络进行反演。

但是一般它们都是连续的数值，所以还要将模型参数表示为二进制[1]:地球物理反演教程其中:Bij=0或1为二进制数;D和U为整数，取决于模型参数的大小和精度。

这样第i个模型参数就用Bij表示为了二进制数。将式(8.45)代入目标函数式(8.43)后再与离散Hopfield神经网络的能量函数进行对比，确立新的等价关系后，就可以进行反演了。

这个新的等价关系式可以参见王家映的《地球物理反演理论》[1]一书。反演的过程大致如下:(1)根据模型参数的大小范围和精度确定D和U，将初始输入模型参数变为二进制数。

设立一个拟合精度标准，如相对均方差ε，设定一个最大迭代次数N(所有神经元的输出都修改一次称为一次迭代)。(2)利用数据方程的G矩阵(在一般情况下需用偏导数矩阵获得)计算网络的权值和阀值。

(3)将二进制初始模型参数输入网络并运行网络。(4)把每次迭代网络输出值变为十进制模型参数，进行正演计算。如果拟合满足精度ε，则停止网络运行并输出反演结果。

否则重复(2)~(4)步直到满足精度或达到最多迭代次数N为止。

在一般情况下，地球物理数据方程的G矩阵是无法用解析式写出的，需要用偏导数矩阵获得，它是依赖于输入参数的，因此网络的每次迭代都要重新计算偏导数矩阵。这个计算量是很大的。因此他的反演过程和最小二乘法相似。

此外，用Hopfield神经网络进行反演同样有可能陷入局部极值点(吸引子)。因此同样受初始模型的影响，需要尽量让初始模型接近真实模型。

8.5.4.2连续Hopfield神经网络(CHNN)[8]1984年，Hopfield把离散Hopfield神经网络发展为连续Hopfield神经网络。

但所有神经元都同步工作，各输入输出量为随时间变化的连续的模拟量，这就使得CHNN比DHNN在信息处理的并行性、实时性方面更接近实际的生物神经网络工作机理。因此利用CHNN进行地球物理反演更加方便。

CHNN可以用常系数微分方程来描述，但用模拟电子线路来描述，则更加形象直观，易于理解。图8.13为连续Hopfield神经网络的拓扑结构[8]。

图8.13连续Hopfield神经网络的拓扑结构[8]图8.13中每个神经元用一个运算放大器模拟，神经元的输入输出用放大器的输入输出电压表示，连接权用电导表示。

每个放大器有一个正向输出和一个反向输出，分别表示兴奋和抑制。每个神经元还有一个用于设置激活电平的外界输入偏置电流作为阀值。这里由于篇幅关系不再累述。感兴趣的读者可以参考其他文献。