【机器学习】集成模型/集成学习:多个模型相结合实现更好的预测
1. 概述
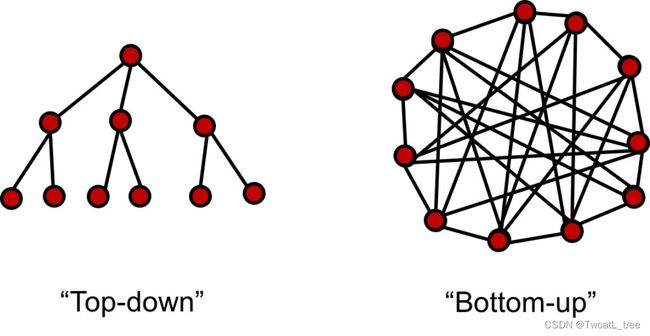
1.1 什么是集成模型/集成学习
"模型集成"和"集成学习"是相同的概念。它们都指的是将多个机器学习模型组合在一起,以提高预测的准确性和稳定性的技术。通过结合多个模型的预测结果,集成学习可以减少单个模型的偏差和方差,并提供更可靠的预测结果。
集成学习原名为Classifier combination / ensemble learning,它是根据训练数据构造一组基分类器(base classifier),通过聚合每个基分类器的输出来进行分类。
基分类器,就是一个小的分类器,单个基分类器的性能取决于它选择的分类算法和训练集。
对于单个性能比较弱的基分类器,我们称为弱分类器。
对于单个性能比较强的基分类器,我们称为强分类器。
多个基分类器集成的思想源于下列直觉:
- 考虑到几个基分类器的分类意见,而不是仅仅依靠一个基分类器的意见 。
- 许多弱分类器的组合至少可以和一个强分类器一样好。
- 一些强分类器的组合(通常)至少和基分类器中最好的一个一样好。
集成是建立各种模型的过程,然后将它们混合以产生更好的预测。与单个模型相比,集成能够实现更精确的预测。在ML比赛中,利用集成通常会带来优势。你可以找到CrowdFlower winners的团队采访,他们用集成赢得了比赛:https://medium.com/kaggle-blog/crowdflower-winners-interview-3rd-place-team-quartet-cead438f8918
1.2 分类器集成的结果
多个分类器集成后的性能一定更好吗?我们带着这个疑问来看下面的例子:
C 1 , C 2 , C 3 C_{1}, C_{2}, C_{3} C1,C2,C3 分别代表了3个基分类器, C ∗ C^{*} C∗ 表示的是三个分类器的结合的最终结果:
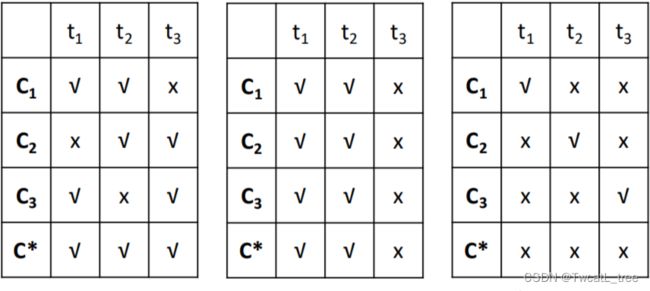
由结果可以看出,多个基分类器的集合不一定犹豫单个基分类器的性能,那么:
什么时候选择集成呢?
基础分类器不会犯同样的错误。
每个基础分类器都是相当准确的。
1.3 构造基分类器的三种方法
实例操作:通过抽样产生多个训练集,并在每个数据集上训练一个基础分类器。
特征操作:通过不同的特征子集生成多个训练集,并在每个数据集上训练一个基础分类器。
算法操作:半随机地调整给定算法中的内部参数,在给定的数据集上生成多个基础分类器。
1.4 多个基分类器如何进行分类
在多个基分类器上进行分类的最简单手段是投票:
对于离散类,在测试集上运行多个基分类器,并选择由最多基分类器预测的类(少数服从多数)。例如一个二分类的数据集,,构造了5个基分类器,对于某个样本有三个基分类器的输出结果是1, 两个是0那么这个时候,总和来看结果就应该是1。
对于连续数值类,对我们基分类器预测的数字进行平均,将平均数作为最终的预测结果。
2. 单一模型存在的问题
单一模型是指只使用一个基础模型来进行预测或分类的方法,例如决策树、支持向量机、神经网络等。
单一模型的优点是简单、易于理解和实现,但也存在一些缺点,主要有以下几个方面:
- 泛化能力不足:单一模型容易受到数据噪声、异常值和过拟合的影响,导致在新的数据上表现不佳。
- 稳定性不高:单一模型对数据的分布和特征的选择非常敏感,稍微改变数据或特征就可能导致预测结果的变化。
- 表达能力有限:单一模型往往只能捕捉数据的某些方面的信息,难以表达数据的复杂性和多样性。
为了解决单一模型存在的问题,我们可以使用集成模型来组合多个基础模型,从而提高预测性能和泛化能力。
3. 简单的集成模型应用
集成模型背后的想法很简单:为什么不使用多个模型并结合它们的预测,而不是依赖一个模型?这样,我们就可以利用不同模型的多样性和互补性,获得更稳健、更准确的预测。

例如,假设我们想要根据客户的年龄、性别、收入和浏览历史来预测客户是否会购买产品。我们可以使用单一模型,例如逻辑回归或决策树,但它可能只能捕获数据中的一些细微差别和模式。或者,我们可以使用多种模型,例如逻辑回归、决策树、k 最近邻和支持向量机,并使用某种规则或算法组合它们的预测。这是集成模型的示例。
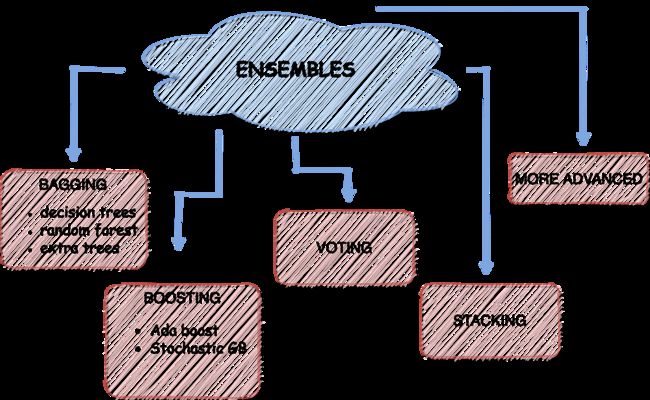
创建和组合多个模型的方法有多种。根据集成模型的实现方式,我们可以将集成模型分为五种主要类型:投票、平均、堆叠、装袋、提升。
3.1 投票

装袋的一个特殊情况是将模型用于分类而不是回归。例如,如果你有三个模型用于预测巴黎是否会下雨,可以进行多数投票,得到“是”作为最终预测结果。这也被称为多数投票集成或多数派集成。
多数投票的优点在于它降低了预测的错误率,意味着它们更有可能是正确的。缺点是它不考虑每个预测的置信度或概率,这意味着它可能忽略了一些有用的信息。
要在Python中使用scikit-learn实现多数投票集成,可以使用VotingClassifier类,将其voting参数设置为’hard’。这个类允许我们指定一个模型列表和一个投票方法(如’hard’或’soft’)来组合它们的预测。
以下是如何使用多数投票进行分类的示例:
from sklearn.ensemble import VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
# 生成分类的随机数据集
X, y = make_classification(n_samples = 1000 , random_state= 42 )
# 将数据集分割为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size= 0.2 , random_state= 42 )
# 定义三个不同的模型
model1 = LogisticRegression(random_state= 42 )
model2 = DecisionTreeClassifier(random_state= 42 )
model3 = SVC(random_state= 42 ,probability= True )
# 使用多数投票集成组合模型
= VotingClassifier(estimators=[( 'lr' , model1), ( 'dt' , model2) , ( 'svc' , model3)], Voting= 'hard' )
# 在训练数据上拟合集成 ensemble.fit
(X_train, y_train)
# 在测试数据上评估集成的性能
print ( f"整体精准度:{ensemble.score(X_test, y_test)* 100 } %" )
3.2 平均
将多个模型的预测结果取平均值是组合多个模型的最简单方式。例如,如果你有三个模型分别预测巴黎的温度为15°C、18°C和20°C,你可以将它们的平均值计算出来,得到最终的预测值为17.67°C。这也被称为均值集成。
取平均的优点在于它降低了预测的方差,意味着它们不太可能偏离真实值太远。缺点在于它也降低了预测的偏差,意味着它们不太可能接近真实值。换句话说,取平均值使得预测更加一致,但也更加保守。
要在Python中使用scikit-learn实现平均集成,对于回归问题,我们可以使用VotingRegressor类,对于分类问题,我们可以使用VotingClassifier类。这些类允许我们指定一组模型和一个投票方法(如’hard’或’soft’)来组合它们的预测。
以下是如何在回归问题中使用平均集成的示例:
# 导入库
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
from sklearn.neighbors import KNeighborsRegressor
from sklearn.ensemble import VotingRegressor
from sklearn.datasets import fetch_california_housing
from sklearn.metrics importmean_squared_error #
加载数据
california = fetch_california_housing (as_frame=真)
X = california.data
y = california.target
# 定义模型
lr = LinearRegression()
dt = DecisionTreeRegressor()
knn = KNeighborsRegressor()
# 创建平均集成
avg = VotingRegressor(estimators=[( 'lr' , lr), ( 'dt ' , dt), ( 'knn' , knn)])
# 对数据进行集成
avg.fit(X, y)
# 进行预测
y_pred = avg.predict(X)
# 评估性能
mse = Mean_squared_error(y, y_pred)
print ( f'MSE: {mse: .2 f} ' )
3.3 堆叠
另一种组合多个模型的方法是将它们用作另一个模型的输入。例如,如果你有三个模型分别预测巴黎的温度为15°C、18°C和20°C,你可以使用它们的预测作为第四个模型的特征,该模型学习如何加权它们并进行最终的预测。这也被称为元学习器或二级学习器。
堆叠的优点在于它可以从每个模型的优点和缺点中学习,从而做出更准确的预测。缺点在于它可能更加复杂,并容易过拟合,意味着它可能在训练数据上表现良好,但在新数据上表现不佳。
要在Python中使用scikit-learn实现堆叠集成,对于回归问题,我们可以使用StackingRegressor类,对于分类问题,我们可以使用StackingClassifier类。这些类允许我们指定一组模型作为基本估算器,以及另一个模型作为最终估算器。
以下是如何在分类问题中使用堆叠集成的示例:
# 导入库
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import StackingClassifier
from sklearn.datasets import load_iris
from sklearn.metrics import precision_score
# 加载数据
X, y = load_iris(return_X_y= True )
# 定义模型
lr = LogisticRegression()
dt = DecisionTreeClassifier()
knn = KNeighborsClassifier()
# 创建堆叠集成
stack = StackingClassifier(estimators=[( 'lr' , lr), ( 'dt' , dt), ( ' knn' , knn)], Final_estimator=LogisticRegression())
# 对数据进行集成
stack.fit(X, y)
# 进行预测
y_pred = stack.predict(X)
# 评估性能
acc = precision_score(y, y_pred)
acc = acc* 100
print ( f'准确度: {acc: .2 f} %' )
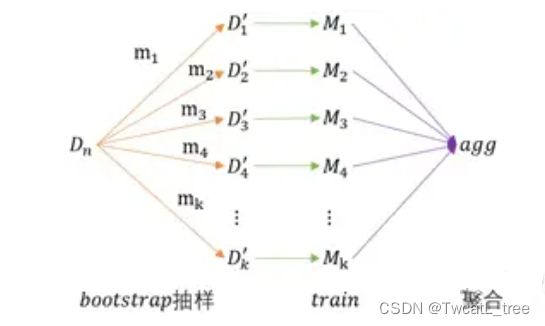
3.4 装袋

第四种组合多个模型的方法是使用数据的不同子集来训练它们。例如,如果你有一个包含1000个观测值的数据集,你可以随机采样500个观测值(可以有重复的观测值),然后使用它们来训练一个模型。你可以多次重复这个过程,从而得到在数据不同子集上训练的不同模型。这也被称为自助聚合或自助法。
自助法的优点在于它降低了预测的方差,意味着它们不太可能偏离真实值太远。缺点在于它不降低预测的偏差,意味着它们仍然有可能接近真实值。换句话说,自助法使预测更加一致但不一定更准确。
要在Python中使用scikit-learn实现自助法集成,对于回归问题,我们可以使用BaggingRegressor类,对于分类问题,我们可以使用BaggingClassifier类。这些类允许我们指定一个基本估算器和创建的自助样本数量。
以下是如何在回归问题中使用bagging ensemble的示例:
# 导入库
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier
from sklearn.datasets import load_iris
from sklearn.metrics import precision_score
# 加载数据
X, y = load_iris(return_X_y= True )
# 定义基础模型
dt = DecisionTreeClassifier()
#创建装袋集成
bag = BaggingClassifier(base_estimator=dt, n_estimators= 10 )
# 在数据上拟合
集成 bag.fit(X, y)
# 进行预测
y_pred = bag.predict(X)
# 评估性能
acc = precision_score(y, y_pred )
acc = acc * 100
print ( f'准确度: {acc: .2 f} %' )
3.5 提升

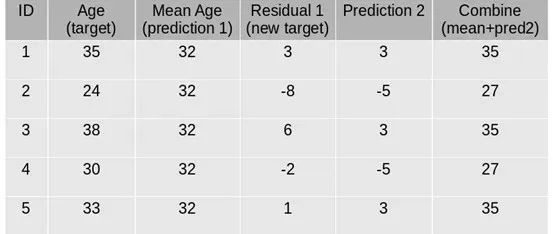
组合多个模型的最后一种方法是以顺序和迭代的方式使用它们。例如,如果你有一个模型预测巴黎的温度为15°C,你可以使用其误差或残差作为另一个模型的输入,该模型试图纠正这些误差并做出更好的预测。你可以多次重复这个过程,得到相互从彼此错误中学习的不同模型。这也被称为自适应提升或AdaBoost。
提升的优点在于它降低了预测的方差和偏差,意味着它们更有可能接近并准确地反映真实值。缺点在于它可能对异常值和噪声更为敏感,意味着它可能对数据过拟合或欠拟合。
要在Python中使用scikit-learn实现提升集成,对于回归问题,我们可以使用AdaBoostRegressor类,对于分类问题,我们可以使用AdaBoostClassifier类。这些类允许我们指定一个基本估算器和提升迭代的次数。
以下是如何在回归问题中使用提升集成的示例:
# 导入库
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import AdaBoostRegressor
from sklearn.datasets import load_iris
from sklearn.metrics importmean_squared_error #
加载数据
X, y = load_iris(return_X_y= True )
# 定义基础模型
dt = DecisionTreeRegressor()
#创建增强集成
boost = AdaBoostRegressor(base_estimator=dt, n_estimators= 10 )
# 根据数据拟合集成
boost.fit(X, y)
# 进行预测
y_pred = boost.predict(X)
# 评估性能
mse = Mean_squared_error(y, y_pred)
打印(f'MSE:{mse:.2 f} ')
4. 分析预测模型的泛化误差
从模型角度看:
- Bias(偏置):衡量一个分类器进行错误预测的趋势。
- Variance(变异度):衡量一个分类器预测结果的偏离程度。
如果一个模型有更小的Bias和Variance 就代表这个模型的泛化性能很好。
5. 几何直观地理解集成学习的四大类型
5.1 装袋法 Bagging(实例操作)
- 将大小为 n n n 的原始数据 D n D_n Dn ,进行Bootstrap抽样(有放回抽样),因此在各抽样数据集 D i ′ D_i' Di′ 中,存在部分元素重复;各抽样数据集的样本容量 m i ≤ n m_i≤n mi≤n
- 将抽样后的数据集,分别独立进行模型学习
- 然后将 k k k 个模型进行聚合;分类:多数投票;回归:平均数、中位数
- 没有一个模型是在整个数据集上训练的
- 如果原始数据集部分元素发生异常变化,可能会影响子模型,而不影响聚合后的模型,
- 因此:“取偏差小 、方差大的基础模型,将其聚合,得到偏差小、方差小的模型”
Bagging = bootstrap aggregating(自举汇聚法)
装袋法思想源于数据越多,性能越好的直觉判断。
具体方法:
通过随机抽样与替换相结合的方式构建新的数据集 。
将原始数据集进行有放回的随机采样次,得到了个数据集,针对这些数据集一共产生个不同的基分类器。对于这个分类器,让他们采用投票法来决定最终的分类结果。
因为袋装法是有放回的随机采样 N N N次,那就有可能有些样本可能永远不会被随机到。因为 N N N个样本,每个样本每次被取到的概率为 1 N \frac{1}{N} N1,那么一共取 N N N次没取到的概率为 ( 1 − 1 N ) N \left ( 1-\frac{1}{N} \right )^{N} (1−N1)N这个值在 N N N很大的时候的极限值 ≈ 0.37 \approx 0.37 ≈0.37。
装袋法的特点:
- 始终使用相同的基分类算法。
- 减少预测的 V a r i a n c e Variance Variance(通过接受一些 B i a s Bias Bias)。
- 对不稳定的分类器(训练集的微小变化会导致预测的巨大变化)有效。
- 可能会使稳定分类器的性能略有下降。
- 基于抽样(构造基分类器的三种方法中的实例操作)和投票的简单方法。
- 多个单独的基分类器可以同步并行进行计算。
- 可以有效的克服数据集中的噪声数据,因为异常值可能会消失( ≈ 0.63 \approx 0.63 ≈0.63)。
- 性能通常比基分类器要好得多,只是偶尔会比基分类器差。
5.2 随机森林法 Random Forest(特征操作)
具有良好深度的决策树就是 低偏差 和 高方差 的模型;因此用决策树做基础模型的Bagging(装袋算法),也称随机森林

- 对于原始数据集的 行:进行Bootstrap抽样(有放回抽样),大小为 m 的样本容量
- 对于原始数据集的 列:随机选择一个特征子集
- 在每个行抽样的数据集中,剩下的数据点(也称袋外点)可以用于相应子模型的交叉验证(以了解每个基础学习者的性能)
- 随着基础模型数量的增加 ,聚合的模型的方差减少
- 偏差(单个模型) ≈ 偏差(聚合后)
- 列采样率: d ′ d \frac{d'}{d} dd′ ;行采样率: m n \frac{m}{n} nm ;如果这两个比值减小,基础模型方差也减小,因此聚合模型的方差也会减少,一般情况固定,不需要认为优化
- 基础模型的个数 k ,为超参数,可以根据交叉验证进行确认最优
- 特征重要性:对每个基础模型的特征的信息增益求和,再在各特征中进行比较,较大信息增益为较重要特征
随机森林法的基分类器是随机树:一棵决策树,但每个节点只考虑一些可能的属性。
也就是说随机树使用的特征空间不是训练集全部的特征空间
- 例如,采用一个固定的比例来选择每个决策树的特征空间大小。
- 随机森林中的每棵树的建立都比一个单独的决策树要简单和快速;但是这种方法增加了模型的 。
森林就是多个随机树的集合
随机森林的超参数:
树的数量B,可以根据“out-of-bag”误差进行调整。
特征子样本大小:随着它的增加,分类器的强度和相关性都增加 ( ⌊ l o g 2 ∣ F ∣ + 1 ⌋ ) \left ( \left \lfloor log_{2}\left | F \right | + 1 \right \rfloor \right ) (⌊log2∣F∣+1⌋)。因为随机森林中的每棵树使用的特征越多,其与森林中其他树的特征重合度就可能越高,导致产生的随机数相似度越大。
可解释性:单个实例预测背后的逻辑可以通过多棵随机树共同决定。
随机森林的特点:
- 随机森林非常强大,可以高效地进行构建。
- 可以并行的进行。
- 对过拟合有很强的鲁棒性。
- 可解释性被牺牲了一部分,因为每个树的特征都是特征集合中随机选取的一部分。
5.3 演进法 Boosting(算法操作)
演进法的思想源于调整基础分类器,使其专注于难以分类的实例的直觉判断。
具体方法:
迭代地改变训练实例的分布和权重,以反映分类器在前一次迭代中的表现。
- 从初始训练集训练出一个基学习器;这时候每个样本的权重都为。
- 每个都会根据上一轮预测结果调整训练集样本的权重。
- 基于调整后的训练集训练一个新的基学习器。
- 重复进行,直到基学习器数量达到开始设置的值。
- 将个基学习器通过加权的投票方法(weighted voting)进行结合。
对于boosting方法,有两个问题需要解决:
- 每一轮学习应该如何改变数据的概率分布
- 如何将各个基分类器组合起来
Boosting集成方法的特点:
- 他的基分类器是决策树或者 OneR 方法。
- 数学过程复杂,但是计算的开销较小;整个过程建立在迭代的采样过程和加权的投票(voting)上。
- 通过迭代的方式不断的拟合残差信息,最终保证模型的精度。
- 比bagging方法的计算开销要大一些。
- 在实际的应用中,boosting的方法略有过拟合的倾向(但是不严重)。
- 可能是最佳的词分类器(gradient boosting)。
5.3.1 演进法实例:AdaBoost
Adaptive Boosting(自适应增强算法):是一种顺序的集成方法(随机森林和 Bagging 都属于并行的集成算法)。
具体方法:
有T个基分类器: C 1 , C 2 , . . . , C i , . . , C T C_{1},C_{2},...,C_{i},..,C_{T} C1,C2,...,Ci,..,CT。
训练集表示为 { x i , y j ∣ j = 1 , 2 , . . . , N } \left \{ x_{i},y_{j}|j=1,2,...,N \right \} {xi,yj∣j=1,2,...,N}。
初始化每个样本的权重都为 1 N \frac{1}{N} N1,即: { w j ( 1 ) = 1 N ∣ j = 1 , 2 , . . . , N } \left \{ w_{j}^{(1)=\frac{1}{N}}|j=1,2,...,N \right \} {wj(1)=N1∣j=1,2,...,N}。
在每个iteration i 中,都按照下面的步骤进行:
计算错误率 error rate
ξ i = ∑ j = 1 N w j ( i ) δ ( C j ( x j ) ≠ y j ) \xi _{i}=\sum _{j=1}^{N} w_{j}^{(i)}\delta (C_{j}(x_{j})\neq y_{j}) ξi=∑j=1Nwj(i)δ(Cj(xj)=yj)
δ ( ) \delta \left ( \right) δ()是一个indicator函数,当函数的条件满足的时候函数值为1;即,当弱分类器 C i C_{i} Ci对样本 x j x_{j} xj进行分类的时候如果分错了就会累积 w j w_{j} wj。
使用 ξ i \xi _{i} ξi来计算每个基分类器 C i C_{i} Ci的重要程度(给这个基分类器分配权重 α i \alpha _{i} αi)
α i = 1 2 l n 1 − ε i ε i \alpha _{i}=\frac{1}{2}ln\frac{1-\varepsilon _{i}}{\varepsilon _{i}} αi=21lnεi1−εi
从这个公式也能看出来,当 C i C_{i} Ci 判断错的样本量越多,得到的 ξ i \xi _{i} ξi就越大,相应的 α i \alpha _{i} αi就越小(越接近0)
根据 α i \alpha _{i} αi来更新每一个样本的权重参数,为了第i+1个iteration做准备:
w j ( i + 1 ) = w j ( i ) Z ( i ) × { e − α i i f C i ( x j ) = y j e α i i f C i ( x j ) ≠ y j w_{j}^{(i+1)}=\frac{w_{j}^{(i)}}{Z^{(i)}}\times \left\{\begin{matrix} e^{-\alpha _{i}} &ifC_{i}(x_{j})=y_{j} \\ e^{\alpha _{i}} & ifC_{i}(x_{j})\neq y_{j} \end{matrix}\right. wj(i+1)=Z(i)wj(i)×{e−αieαiifCi(xj)=yjifCi(xj)=yj
样本j的权重由 w j ( i ) w_{j}^{(i)} wj(i)变成 w j ( i + 1 ) w_{j}^{(i+1)} wj(i+1)这个过程中发生的事情是:如果这个样本在第i个iteration中被判断正确了,他的权重就会在原本KaTeX parse error: Expected '}', got 'EOF' at end of input: w_{j}^{(i)}的基础上乘以 e − α i e^{-\alpha _{i}} e−αi;根据上面的知识 α i > 0 \alpha _{i} > 0 αi>0因此 − α i < 0 -\alpha _{i} < 0 −αi<0所以根据公式我们可以知道,那些被分类器预测错误的样本会有一个大的权重;而预测正确的样本则会有更小的权重。
Z ( i ) Z^{(i)} Z(i)是一个normalization项,为了保证所有的权重相加之和为1。
最终将所有的 C i C_{i} Ci按照权重进行集成
持续完成从i=2,…,T的迭代过程,但是当 ε i > 0.5 \varepsilon_{i} > 0.5 εi>0.5的时候需要重新初始化样本的权重最终采用的集成模型进行分类的公式:
C ∗ ( x ) = a r g m a x y ∑ i = 1 T α i δ ( C i ( x ) = y ) C^{*}(x)=argmax_{y}\sum _{i=1}^{T}\alpha _{i}\delta (C_{i}(x)=y) C∗(x)=argmaxy∑i=1Tαiδ(Ci(x)=y)
这个公式的意思大概是:例如我们现在已经得到了3个基分类器,他们的权重分别是0.3, 0.2, 0.1所以整个集成分类器可以表示为:
C ( x ) = ∑ i = 1 T α i C i ( x ) = 0.3 C 1 ( x ) + 0.2 C 2 ( x ) + 0.1 C 3 ( x ) C(x)=\sum _{i=1}^{T}\alpha _{i}C_{i}(x)=0.3C_{1}(x)+0.2C_{2}(x)+0.1C_{3}(x) C(x)=∑i=1TαiCi(x)=0.3C1(x)+0.2C2(x)+0.1C3(x)
如果类别标签一共只有0, 1那就最终的C(x)对于0的值大还是对于1的值大了。
只要每一个基分类器都比随机预测的效果好,那么最终的集成模型就会收敛到一个强很多的模型。
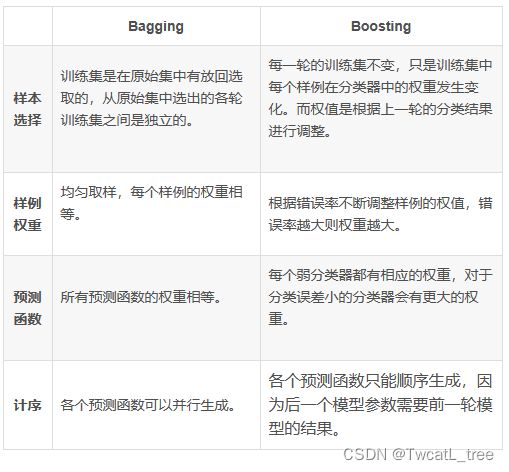
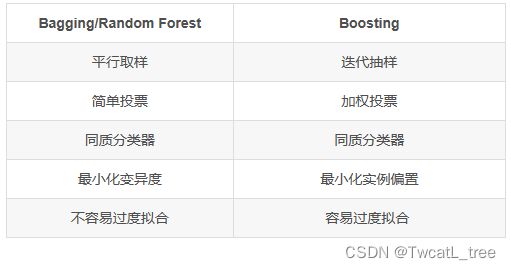
5.3.2 装袋法/随机森林和演进法对比
5.4 堆叠法 Stacking
堆叠法的思想源于在不同偏置的算法范围内平滑误差的直觉。
方法:采用多种算法,这些算法拥有不同的偏置
在基分类器(level-0 model) 的输出上训练一个元分类器(meta-classifier)也叫level-1 model
了解哪些分类器是可靠的,并组合基分类器的输出 使用交叉验证来减少偏置
Level-0:基分类器
给定一个数据集 ( X , y ) 可以是SVM, Naive Bayes, DT等
Level-1:集成分类器
在Level-0分类器的基础上构建新的attributes
每个Level-0分类器的预测输出都会加入作为新的attributes;如果有M个Level-0分离器最终就会加入M个attributes
删除或者保持原本的数据X 考虑其他可用的数据(NB概率分数,SVM权重) 训练meta-classifier来做最终的预测
stacking方法的特点:
- 结合多种不同的分类器
- 数学表达简单,但是实际操作耗费计算资源
- 通常与基分类器相比,stacking的结果一般好于最好的基分类器
PS:读到这里你大概已经了解集成学习了,如果你想更深入了解的话可以继续读下去
6. 深入介绍集成技术
6.1 集成学习介绍
我们通过一个例子来理解集成学习的概念。假设你是一名电影导演,你依据一个非常重要且有趣的话题创作了一部短片。现在,你想在公开发布前获得影片的初步反馈(评级)。有哪些可行的方法呢?
A:可以请一位朋友为电影打分。
于是完全有可能出现这种结果:你所选择的人由于非常爱你,并且不希望给你这部糟糕的影片打1星评级来伤害你脆弱的小心脏。
B:另一种方法是让你的5位同事评价这部电影。
这个办法应该更好,可能会为电影提供更客观诚实的评分。但问题依然存在。这5个人可能不是电影主题方面的“专家”。当然,他们可能懂电影摄制,镜头或音效,但他们可能并不是黑色幽默的最佳评判者。
C:让50个人评价这部电影呢?
其中一些可以是你的朋友,可以是你的同事,甚至是完完全全的陌生人。
在这种情况下,回应将更加普遍化和多样化,因为他们拥有不同的技能。事实证明,与我们之前看到的情况相比,这是获得诚实评级的更好方法。
通过这些例子,你可以推断,与个人相比,不同群体的人可能会做出更好的决策。与单一模型相比,各种不同模型也是这个道理。机器学习中的多样化是通过称为集成学习(Ensemble learning)的技术实现的。
现在你已经掌握了集成学习的要旨,接下来让我们看看集成学习中的各种技术及其实现。
6.2 简单集成技术
这一节中,我们会看一些简单但是强大的技术,比如:
- 最大投票法
- 平均法
- 加权平均法
6.2.1 最大投票法
最大投票方法通常用于分类问题。这种技术中使用多个模型来预测每个数据点。每个模型的预测都被视为一次“投票”。大多数模型得到的预测被用作最终预测结果。
例如,当你让5位同事评价你的电影时(最高5分); 我们假设其中三位将它评为4,而另外两位给它一个5。由于多数人评分为4,所以最终评分为4。你可以将此视为采用了所有预测的众数(mode)。
最大投票的结果有点像这样:
示例代码:
这里x_train由训练数据中的自变量组成,y_train是训练数据的目标变量。验证集是x_test(自变量)和y_test(目标变量)。
model1 = tree.DecisionTreeClassifier()
model2 = KNeighborsClassifier()
model3= LogisticRegression()
model1.fit(x_train,y_train)
model2.fit(x_train,y_train)
model3.fit(x_train,y_train)
pred1=model1.predict(x_test)
pred2=model2.predict(x_test)
pred3=model3.predict(x_test)
final_pred = np.array([])
for i in range(0,len(x_test)):
final_pred =np.append(final_pred, mode([pred1[i], pred2[i], pred3[i]]))
或者,你也可以在sklearn中使用“VotingClassifier”模块,如下所示:
from sklearn.ensemble import VotingClassifier
model1 = LogisticRegression(random_state=1)
model2 = tree.DecisionTreeClassifier(random_state=1)
model = VotingClassifier(estimators=[(‘lr’, model1), (‘dt’, model2)], voting=‘hard’)
model.fit(x_train,y_train)
model.score(x_test,y_test)
6.2.2 平均法
类似于最大投票技术,这里对每个数据点的多次预测进行平均。在这种方法中,我们从所有模型中取平均值作为最终预测。平均法可用于在回归问题中进行预测或在计算分类问题的概率时使用。
例如,在下面的情况中,平均法将取所有值的平均值。
即(5 + 4 + 5 + 4 + 4)/ 5 = 4.4

示例代码:
model1 = tree.DecisionTreeClassifier()
model2 = KNeighborsClassifier()
model3= LogisticRegression()
model1.fit(x_train,y_train)
model2.fit(x_train,y_train)
model3.fit(x_train,y_train)
pred1=model1.predict_proba(x_test)
pred2=model2.predict_proba(x_test)
pred3=model3.predict_proba(x_test)
finalpred=(pred1+pred2+pred3)/3
2.3 加权平均法
这是平均法的扩展。为所有模型分配不同的权重,定义每个模型的预测重要性。例如,如果你的两个同事是评论员,而其他人在这方面没有任何经验,那么与其他人相比,这两个朋友的答案就更加重要。
计算结果为[(5 * 0.23)+(4 * 0.23)+(5 * 0.18)+(4 * 0.18)+(4 * 0.18)] = 4.41。

示例代码:
model1 = tree.DecisionTreeClassifier()
model2 = KNeighborsClassifier()
model3= LogisticRegression()
model1.fit(x_train,y_train)
model2.fit(x_train,y_train)
model3.fit(x_train,y_train)
pred1=model1.predict_proba(x_test)
pred2=model2.predict_proba(x_test)
pred3=model3.predict_proba(x_test)
finalpred=(pred1 0.3+pred20.3+pred3*0.4)
6.3 高级集成技术
我们已经介绍了基础的集成技术,让我们继续了解高级的技术。
6.3.1 堆叠(Stacking)
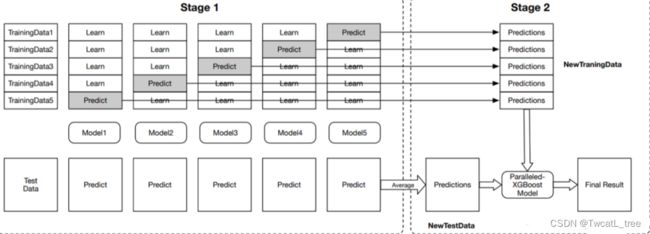
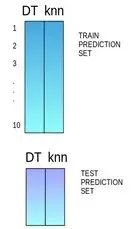
堆叠是一种集成学习技术,它使用多个模型(例如决策树,knn或svm)的预测来构建新模型。该新模型用于对测试集进行预测。以下是简单堆叠集成法的逐步解释:
第一步:把训练集分成10份

第二步:基础模型(假设是决策树)在其中9份上拟合,并对第10份进行预测。
第三步:对训练集上的每一份如此做一遍。

第四步:然后将基础模型(此处是决策树)拟合到整个训练集上。
第五步:使用此模型,在测试集上进行预测。

第六步:对另一个基本模型(比如knn)重复步骤2到4,产生对训练集和测试集的另一组预测。

第七步:训练集预测被用作构建新模型的特征。
第八步:该新模型用于对测试预测集(test prediction set,上图的右下角)进行最终预测。
示例代码:
我们首先定义一个函数来对n折的训练集和测试集进行预测。此函数返回每个模型对训练集和测试集的预测。
def Stacking(model,train,y,test,n_fold):
folds=StratifiedKFold(n_splits=n_fold,random_state=1)
test_pred=np.empty((test.shape[0],1),float)
train_pred=np.empty((0,1),float)
for train_indices,val_indices in folds.split(train,y.values):
x_train,x_val=train.iloc[train_indices],train.iloc[val_indices]
y_train,y_val=y.iloc[train_indices],y.iloc[val_indices]
model.fit(X=x_train,y=y_train)
train_pred=np.append(train_pred,model.predict(x_val))
test_pred=np.append(test_pred,model.predict(test))
return test_pred.reshape(-1,1),train_pred
现在我们将创建两个基本模型:决策树和knn。
model1 = tree.DecisionTreeClassifier(random_state=1)
test_pred1 ,train_pred1=Stacking(model=model1,n_fold=10, train=x_train,test=x_test,y=y_train)
train_pred1=pd.DataFrame(train_pred1)
test_pred1=pd.DataFrame(test_pred1)
model2 = KNeighborsClassifier()
test_pred2 ,train_pred2=Stacking(model=model2,n_fold=10,train=x_train,test=x_test,y=y_train)
train_pred2=pd.DataFrame(train_pred2)
test_pred2=pd.DataFrame(test_pred2)
创建第三个模型,逻辑回归,在决策树和knn模型的预测之上。
df = pd.concat([train_pred1, train_pred2], axis=1)
df_test = pd.concat([test_pred1, test_pred2], axis=1)
model = LogisticRegression(random_state=1)
model.fit(df,y_train)
model.score(df_test, y_test)
为了简化上面的解释,我们创建的堆叠模型只有两层。决策树和knn模型建立在零级,而逻辑回归模型建立在第一级。其实可以随意的在堆叠模型中创建多个层次。
6.3.2 混合(Stacking)
混合遵循与堆叠相同的方法,但仅使用来自训练集的一个留出(holdout)/验证集来进行预测。换句话说,与堆叠不同,预测仅在留出集上进行。留出集和预测用于构建在测试集上运行的模型。以下是混合过程的详细说明:
第一步:原始训练数据被分为训练集合验证集。

第二步:在训练集上拟合模型。
第三步:在验证集和测试集上进行预测。

第四步:验证集及其预测用作构建新模型的特征。
第五步:该新模型用于对测试集和元特征(meta-features)进行最终预测。
示例代码:
我们将在训练集上建立两个模型,决策树和knn,以便对验证集进行预测。
model1 = tree.DecisionTreeClassifier()
model1.fit(x_train, y_train)
val_pred1=model1.predict(x_val)
test_pred1=model1.predict(x_test)
val_pred1=pd.DataFrame(val_pred1)
test_pred1=pd.DataFrame(test_pred1)
model2 = KNeighborsClassifier()
model2.fit(x_train,y_train)
val_pred2=model2.predict(x_val)
test_pred2=model2.predict(x_test)
val_pred2=pd.DataFrame(val_pred2)
test_pred2=pd.DataFrame(test_pred2)
结合元特征和验证集,构建逻辑回归模型以对测试集进行预测。
df_val=pd.concat([x_val, val_pred1,val_pred2],axis=1)
df_test=pd.concat([x_test, test_pred1,test_pred2],axis=1)
model = LogisticRegression()
model.fit(df_val,y_val)
model.score(df_test,y_test)
6.3.3 Bagging
Bagging背后的想法是结合多个模型的结果(例如,所有决策树)来获得泛化的结果。这有一个问题:如果在同样一组数据上创建所有模型并将其组合起来,它会有用吗?这些模型极大可能会得到相同的结果,因为它们获得的输入相同。那我们该如何解决这个问题呢?其中一种技术是自举(bootstrapping)。
Bootstrapping是一种采样技术,我们有放回的从原始数据集上创建观察子集,子集的大小与原始集的大小相同。
Bagging(或Bootstrap Aggregating)技术使用这些子集(包)来获得分布的完整概念(完备集)。为bagging创建的子集的大小也可能小于原始集。
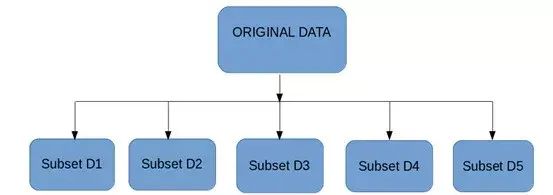
第一步:从原始数据集有放回的选择观测值来创建多个子集。
第二步:在每一个子集上创建一个基础模型(弱模型)。
第三步:这些模型同时运行,彼此独立。
第四步:通过组合所有模型的预测来确定最终预测。
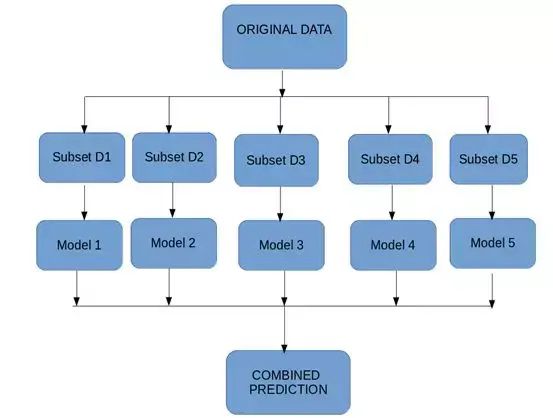
6.3.4 Boosting
在我们进一步讨论之前,这里有另一个问题:如果第一个模型错误地预测了某一个数据点,然后接下来的模型(可能是所有模型),将预测组合起来会提供更好的结果吗?Boosting就是来处理这种情况的。
Boosting是一个顺序过程,每个后续模型都会尝试纠正先前模型的错误。后续的模型依赖于之前的模型。接下来一起看看boosting的工作方式:
第一步:从原始数据集创建一个子集。
第二步:最初,所有数据点都具有相同的权重。
第三步:在此子集上创建基础模型。
第四步:该模型用于对整个数据集进行预测。

第五步:使用实际值和预测值计算误差。
第六步:预测错误的点获得更高的权重。(这里,三个错误分类的蓝色加号点将被赋予更高的权重)
第七步:创建另一个模型并对数据集进行预测(此模型尝试更正先前模型中的错误)。
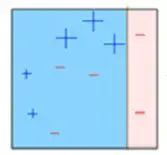
第八步:类似地,创建多个模型,每个模型校正先前模型的错误。
第九步:最终模型(强学习器)是所有模型(弱学习器)的加权平均值。
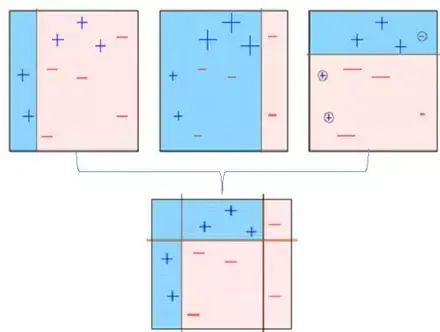
因此,boosting算法结合了许多弱学习器来形成一个强学习器。单个模型在整个数据集上表现不佳,但它们在数据集的某些部分上表现很好。因此,每个模型实际上提升了集成的整体性能。

6.4基于Bagging和Boosting的算法
Bagging和Boosting是机器学习中最常用的两种技术。在本节中,我们将详细介绍它们。以下是我们将关注的算法:
Bagging 算法:
- Bagging meta-estimator
- 随机森林
Boosting算法:
- AdaBoost
- GBM
- XGBM
- Light GBM
- CatBoost
对于本节中讨论的所有算法,我们将遵循以下顺序:
- 算法介绍
- 示例代码
- 参数
本文中,我使用了贷款预测问题。你可以从此处下载数据集。请注意,对于每种算法,某些代码(读取数据,划分训练测试集等)将是相同的。为了避免重复,我在下面编写了相同的代码,并且只对算法相关的代码进行进一步讨论。
#importing important packages
import pandas as pd
import numpy as np
#reading the dataset
df=pd.read_csv(“/home/user/Desktop/train.csv”)
#filling missing values
df[‘Gender’].fillna(‘Male’, inplace=True)
同理,对所有列进行值填充。本文只考虑所讨论的主题,已跳过EDA,缺失值和异常值处理等步骤。要了解这些主题,可以阅读此文:Ultimate guide for Data Explorationin Python using NumPy, Matplotlib and Pandas.
#split dataset into train and test
from sklearn.model_selection import train_test_split
train, test = train_test_split(df, test_size=0.3, random_state=0)
x_train=train.drop(‘Loan_Status’,axis=1)
y_train=train[‘Loan_Status’]
x_test=test.drop(‘Loan_Status’,axis=1)
y_test=test[‘Loan_Status’]
#create dummies
x_train=pd.get_dummies(x_train)
x_test=pd.get_dummies(x_test)
让我们来探索bagging和boosting算法。
6.4.1 Bagging meta-estimator
Bagging meta-estimator是一种集成算法,可用于分类(BaggingClassifier)和回归(BaggingRegressor)问题。它采用典型的bagging技术进行预测。以下是Bagging meta-estimator算法的步骤:
第一步:从原始数据集(Bootstrapping)创建随机子集。
第二步:数据集的子集包括所有特征。
第三步用户指定的基础估计器在这些较小的集合上拟合。
第四步:将每个模型的预测结合起来得到最终结果。
示例代码:
from sklearn.ensemble import BaggingClassifier
from sklearn import tree
model = BaggingClassifier(tree.DecisionTreeClassifier(random_state=1))
model.fit(x_train, y_train)
model.score(x_test,y_test)
0.75135135135135134
回归问题示例代码:
from sklearn.ensemble import BaggingRegressor
model = BaggingRegressor(tree.DecisionTreeRegressor(random_state=1))
model.fit(x_train, y_train)
model.score(x_test,y_test)
算法中用到的参数:
- base_estimator
-
- 定义了在随机子集上拟合所用的基础估计器
- 没有指明时,默认使用决策树
- n_estimators
-
- 创建的基础估计器数量
- 要小心微调这个参数,因为数字越大运行时间越长,相反太小的数字可能无法提供最优结果
- max_samples
-
- 该参数控制子集的大小
- 它是训练每个基础估计器的最大样本数量
- max_features
-
- 控制从数据集中提取多少个特征
- 它是训练每个基础估计器的最大特征数量
- n_jobs
-
- 同时运行的job数量
- 将这个值设为你系统的CPU核数
- 如果设为-1,这个值会被设为你系统的CPU核数
- random_state
-
- 定义了随机分割的方法。当两个模型的random_state值一样时,它们的随机选择也一样
- 如果你想对比不同的模型,这个参数很有用
6.4.2 随机森林
随机森林是另一种遵循bagging技术的集成机器学习算法。它是bagging-estimator算法的扩展。随机森林中的基础估计器是决策树。与bagging meta-estimator不同,随机森林随机选择一组特征,这些特征用于决定决策树的每个节点处的最佳分割。
随机森林的具体步骤如下:
第一步:从原始数据集(Bootstrapping)创建随机子集。
第二步:在决策树中的每个节点处,仅考虑一组随机特征来决定最佳分割。
第三步:在每个子集上拟合决策树模型。
第四步:通过对所有决策树的预测求平均来计算最终预测。
注意:随机林中的决策树可以构建在数据和特征的子集上。特别地,sklearn中的随机森林使用所有特征作为候选,并且候选特征的随机子集用于在每个节点处分裂。
总而言之,随机森林随机选择数据点和特征,并构建多个树(森林)。
示例代码:
from sklearn.ensemble import RandomForestClassifier
model= RandomForestClassifier(random_state=1)
model.fit(x_train, y_train)
model.score(x_test,y_test)
0.77297297297297296
你可以通过在随机林中使用model.feature_importances_来查看特征重要性。
for i, j in sorted(zip(x_train.columns, model.feature_importances_)):
print(i, j)
结果如下:
ApplicantIncome 0.180924483743
CoapplicantIncome 0.135979758733
Credit_History 0.186436670523
.
.
.
Property_Area_Urban 0.0167025290557
Self_Employed_No 0.0165385567137
Self_Employed_Yes 0.0134763695267
回归问题示例代码:
from sklearn.ensemble import RandomForestRegressor
model= RandomForestRegressor()
model.fit(x_train, y_train)
model.score(x_test,y_test)
参数:
- n_estimators
-
- 定义随机森林中要创建的决策树数量
- 通常,越高的值会让预测更强大更稳定,但是过高的值会让训练时间很长
- criterion
-
- 定义了分割用的函数
- 该函数用来衡量使用每个特征分割的质量从而选择最佳分割
- max_features
-
- 定义了每个决策树中可用于分割的最大特征数量
- 增加最大特征数通常可以改善性能,但是一个非常高的值会减少各个树之间的差异性
- max_depth
-
- 随机森林有多个决策树,此参数定义树的最大深度
- min_samples_split
-
- 用于在尝试拆分之前定义叶节点中所需的最小样本数
- 如果样本数小于所需数量,则不分割节点
- min_samples_leaf
-
- 定义了叶子节点所需的最小样本数
- 较小的叶片尺寸使得模型更容易捕获训练数据中的噪声
- max_leaf_nodes
-
- 此参数指定每个树的最大叶子节点数
- 当叶节点的数量变得等于最大叶节点时,树停止分裂
- n_jobs
-
- 这表示并行运行的作业数
- 如果要在系统中的所有核心上运行,请将值设置为-1
- random_state
-
- 此参数用于定义随机选择
- 它用于各种模型之间的比较
6.4.3 AdaBoost
自适应增强或AdaBoost是最简单的boosting算法之一。通常用决策树来建模。创建多个顺序模型,每个模型都校正上一个模型的错误。AdaBoost为错误预测的观测值分配权重,后续模型来正确预测这些值。
以下是执行AdaBoost算法的步骤:
第一步:最初,数据集中的所有观察值都具有相同的权重。
第二步:在数据子集上建立一个模型。
第三步:使用此模型,可以对整个数据集进行预测。
第四步:通过比较预测值和实际值来计算误差。
第五步:在创建下一个模型时,会给预测错误的数据点赋予更高的权重。
第六步:可以使用误差值确定权重。例如,误差越大,分配给观察值的权重越大。
第七步:重复该过程直到误差函数没有改变,或达到估计器数量的最大限制。
示例代码:
from sklearn.ensemble import AdaBoostClassifier
model = AdaBoostClassifier(random_state=1)
model.fit(x_train, y_train)
model.score(x_test,y_test)
0.81081081081081086
回归问题示例代码:
from sklearn.ensemble import AdaBoostRegressor
model = AdaBoostRegressor()
model.fit(x_train, y_train)
model.score(x_test,y_test)
参数:
- base_estimators
-
- 它用于指定基础估计器的类型,即用作基础学习器的机器学习算法
- n_estimators
-
- 它定义了基础估计器的数量
- 默认值为10,但可以设为较高的值以获得更好的性能
- learning_rate
-
- 此参数控制估计器在最终组合中的贡献
- 在learning_rate和n_estimators之间需要进行权衡
- max_depth
-
- 定义单个估计器的最大深度
- 调整此参数以获得最佳性能
- n_jobs
-
- 指定允许使用的处理器数
- 将值设为-1,可以使用允许的最大处理器数量
- random_state
-
- 用于指定随机数据拆分的整数值
- 如果给出相同的参数和训练数据,random_state的确定值将始终产生相同的结果
6.4.4 Gradient Boosting(梯度提升GBM)
Gradient Boosting或GBM是另一种集成机器学习算法,适用于回归和分类问题。GBM使用boosting技术,结合了许多弱学习器,以形成一个强大的学习器。回归树用作基础学习器,每个后续的树都是基于前一棵树计算的错误构建的。
我们将使用一个简单的例子来理解GBM算法。我们会使用以下数据预测一群人的年龄:

第一步:假设平均年龄是数据集中所有观测值的预测值。
第二步:使用该平均预测值和年龄的实际值来计算误差:

第三步:使用上面计算的误差作为目标变量创建树模型。我们的目标是找到最佳分割以最小化误差。
第四步:该模型的预测与预测1相结合:
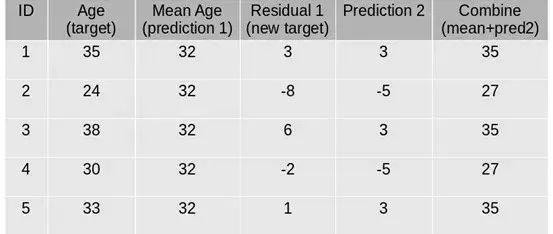
第五步:上面计算的这个值是新的预测。
第六步:使用此预测值和实际值计算新误差:

第七步:重复步骤2到6,直到最大迭代次数(或误差函数不再改变)
示例代码:
from sklearn.ensemble import GradientBoostingClassifier
model= GradientBoostingClassifier(learning_rate=0.01,random_state=1)
model.fit(x_train, y_train)
model.score(x_test,y_test)
0.81621621621621621
回归问题示例代码:
from sklearn.ensemble import GradientBoostingRegressor
model= GradientBoostingRegressor()
model.fit(x_train, y_train)
model.score(x_test,y_test)
参数:
- min_samples_split
-
- 定义考虑被拆分的节点中所需的最小样本数(或观察值数)
- 用于控制过配合。较高的值会阻止模型学习关系,这种关系可能对为一棵树选择的特定样本高度特定
- min_samples_leaf
-
- 定义终端或叶节点中所需的最小样本数
- 一般来说,应该为不平衡的分类问题选择较低的值,因为少数群体占大多数的地区将非常小
- min_weight_fraction_leaf
-
- 与min_samples_leaf类似,但定义为观察总数的一个比例而不是整数
- max_depth
-
- 树的最大深度。
- 用于控制过拟合,因为更高的深度将让模型学习到非常特定于某个样本的关系
- 应该使用CV进行调整
- max_leaf_nodes
-
- 树中终端节点或叶子的最大数量
- 可以用于代替max_depth。由于创建了二叉树,因此深度’n’将产生最多2 ^ n个叶子
- 如果它被定义,则GBM会忽略max_depth
- max_features
-
- 搜索最佳拆分时要考虑的特征数量。这些特征将被随机选择。
- 作为一个经验法则,特征总数的平方根效果很好,但我们可以尝试直到特征总数的30-40%。
- 较高的值可能导致过度拟合,但通常取决于具体情况。
6.4.5 XGBoost
XGBoost(extreme Gradient Boosting)是梯度提升算法的高级实现。实践证明,XGBoost是一种高效的ML算法,广泛应用于机器学习竞赛和黑客马拉松。 XGBoost具有很高的预测能力,几乎比其他梯度提升技术快10倍。它还包括各种正规化,可减少过拟合并提高整体性能。因此,它也被称为“正则化提升”技术。
让我们看看XGBoost为何比其他技术更好:
- 正则化:
-
- 标准GBM实现没有像XGBoost那样的正则化
- 因此,XGBoost还有助于减少过拟合
- 并行处理:
-
- XGBoost实现并行处理,并且比GBM更快
- XGBoost还支持Hadoop上的实现
- 高灵活性:
-
- XGBoost允许用户自定义优化目标和评估标准,为模型添加全新维度
- 处理缺失值:
-
- XGBoost有一个内置的例程来处理缺失值
- 树剪枝:
-
- XGBoost先进行分割,直到指定的max_depth,然后开始向后修剪树并删除没有正向增益的分割
- 内置交叉验证:
-
- XGBoost允许用户在提升过程的每次迭代中运行交叉验证,因此很容易在一次运行中获得精确的最佳提升迭代次数
示例代码:
由于XGBoost会自行处理缺失值,因此你不必再处理。你可以跳过上述代码中缺失值插补的步骤。如下展示了如何应用xgboost:
import xgboost as xgb
model=xgb.XGBClassifier(random_state=1,learning_rate=0.01)
model.fit(x_train, y_train)
model.score(x_test,y_test)
0.82702702702702702
回归问题示例代码:
import xgboost as xgb
model=xgb.XGBRegressor()
model.fit(x_train, y_train)
model.score(x_test,y_test)
参数:
- nthread
-
- 这用于并行处理,应输入系统中的核心数
- 如果你希望在所有核心上运行,请不要输入此值。该算法将自动检测
- eta
-
- 类似于GBM中的学习率
- 通过缩小每一步的权重,使模型更加健壮
- min_child_weight
-
- 定义子节点中所有观察值的最小权重和
- 用于控制过拟合。较高的值会阻止模型学习关系,这种关系可能高度特定于为某个树所选的具体样本
- max_depth
-
- 它用于定义最大深度
- 更高的深度将让模型学习到非常特定于某个样本的关系
- max_leaf_nodes
-
- 树中终端节点或叶子的最大数量
- 可以用来代替max_depth。由于创建了二叉树,因此深度’n’将产生最多2 ^ n个叶子
- 如果已定义,则GBM将忽略max_depth
- gamma
-
- 仅当产生的分割能给出损失函数的正向减少时,才分割节点。Gamma指定进行分割所需的最小损失减少量。
- 使算法保守。值可能会根据损失函数而有所不同,因此应进行调整
- subsample
-
- 与GBM的子样本相同。表示用于每棵树随机采样的观察值的比例。
- 较低的值使算法更加保守并防止过拟合,但是太小的值可能导致欠拟合。
- colsample_bytree
-
- 它类似于GBM中的max_features
- 表示要为每个树随机采样的列的比例
6.4.6 Light GBM
在讨论Light GBM如何工作之前,先理解为什么在我们有如此多其他算法时(例如我们上面看到的算法)我们还需要这个算法。当数据集非常大时,Light GBM会击败所有其他算法。与其他算法相比,Light GBM在较大的数据集上运行所需的时间较短。
LightGBM是一个梯度提升框架,它使用基于树的算法并遵循逐叶子的方式(leaf-wise),而其他算法以逐层级(level-wise)模式工作。下图帮助你更好地理解二者差异:


逐叶子方式可能在较小的数据集上导致过拟合,但可以通过使用’max_depth’参数来避免这种情况。你可以在本文中阅读有关Light GBM及其与XGB比较的更多信息。
示例代码:
import lightgbm as lgb
train_data=lgb.Dataset(x_train,label=y_train)
#define parameters
params = {‘learning_rate’:0.001}
model= lgb.train(params, train_data, 100)
y_pred=model.predict(x_test)
for i in range(0,185):
if y_pred[i]>=0.5:
y_pred[i]=1
else:
y_pred[i]=0
0.81621621621621621
回归问题示例代码:
import lightgbm as lgb
train_data=lgb.Dataset(x_train,label=y_train)
params = {‘learning_rate’:0.001}
model= lgb.train(params, train_data, 100)
from sklearn.metrics import mean_squared_error
rmse=mean_squared_error(y_pred,y_test)**0.5
参数:
- num_iterations
-
- 它定义了要执行的提升迭代次数
- num_leaves
-
- 此参数用于设置要在树中形成的叶子数
- 在Light GBM的情况下,由于拆分是按逐叶子方式而不是深度方式进行的,因此num_leaves必须小于2 ^(max_depth),否则可能导致过拟合
- min_data_in_leaf
-
- 非常小的值可能导致过拟合
- 它也是处理过拟合的最重要的参数之一
- max_depth
-
- 它指定树可以生长到的最大深度或级别
- 此参数的值非常高可能会导致过拟合
- bagging_fraction
-
- 它用于指定每次迭代使用的数据比例
- 此参数通常用于加速训练
- max_bin
-
- 定义特征值将被分桶的最大分箱数
- 较小的max_bin值可以节省大量时间,因为它在离散分箱中存储特征值,这在计算开销上是便宜的
6.4.7 CatBoost
处理类别型变量是一个繁琐的过程,尤其是你有大量此类变量时。当你的类别变量有很多标签(即它们是高度基数)时,对它们执行one-hot编码会指数级的增加维度,会让数据集的使用变得非常困难。
CatBoost可以自动处理类别型变量,并且不需要像其他机器学习算法那样进行大量数据预处理。这篇文章详细解释了CatBoost。
示例代码:
CatBoost算法有效地处理类别型变量。因此,无需对变量执行one-hot编码。只需加载文件,估算缺失值,就可以了:
from catboost import CatBoostClassifier
model=CatBoostClassifier()
categorical_features_indices = np.where(df.dtypes != np.float)[0]
model.fit(x_train,y_train,cat_features=([ 0, 1, 2, 3, 4, 10]),eval_set=(x_test, y_test))
model.score(x_test,y_test)
0.80540540540540539
回归问题示例代码:
from catboost import CatBoostRegressor
model=CatBoostRegressor()
categorical_features_indices = np.where(df.dtypes != np.float)[0]
model.fit(x_train,y_train,cat_features=([ 0, 1, 2, 3, 4, 10]),eval_set=(x_test, y_test))
model.score(x_test,y_test)
参数:
- loss_function
-
- 定义用于训练的度量标准
- iterations
-
- 可以构建最多多少棵树
- 树的最终数量可能小于或等于此数字
- learning_rate
-
- 定义学习率
- 用于减少梯度步骤
- border_count
-
- 它指定数值型特征的拆分数
- 它类似于max_bin参数
- depth
-
- 定义树的深度
- random_seed
-
- 此参数类似于我们之前看到的’random_state’参数
- 它是一个整数值,用于定义训练的随机种子
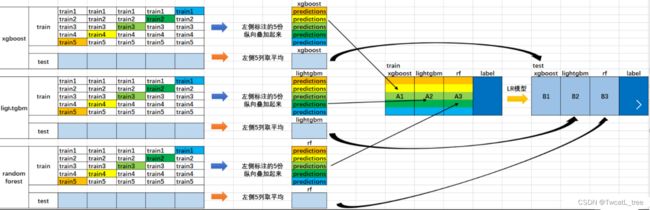
7. 给kaggle新手的入门教程(中文完全注释):7种模型集成学习建模方法(xgBst/eNet…)
#
#给kaggle新手的入门教程(中文完全注释):7种模型集成学习建模方法(xgBst/eNet...)
#
#
#
#
#
#
#
#
# 作者:KeithFish
# GitHub:KeithFish (https://github.com/KeithFish)
# 欢迎留言交流,转载请注明出处
#
#
#
#
#
#
#
#
#
#导入计算模块,对模块大致功能注解:
#numpy支持矩阵运算
#pandas用来做数据清洗,像是python中的excel(支持将数据以.csv格式输出至本地)
#sklearn用来进一步制作数据集(支持数据的导入和数据的导出),含有SVM支持向量机、DT决策树、KNN近邻、LR逻辑回归等封装好的模型,支持对数据进行交叉验证以调参。
#mlxtend用来实现集成学习:bagging, boosting, stacking
#lightgbm内有boosting tree(相比xgboost,改进了生成节点的方式)
#xgboost内有boosting tree
#os用来读取文件
import numpy as np # linear algebra
import pandas as pd #
from datetime import datetime
from scipy.stats import skew # for some statistics
from scipy.special import boxcox1p
from scipy.stats import boxcox_normmax
from sklearn.linear_model import ElasticNetCV, LassoCV, RidgeCV
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.svm import SVR
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import RobustScaler
from sklearn.model_selection import KFold, cross_val_score
from sklearn.metrics import mean_squared_error
from mlxtend.regressor import StackingCVRegressor
from xgboost import XGBRegressor
from lightgbm import LGBMRegressor
import os
#######################################################数据导入和特征提取-【开始】################################################################################
#显示当前编译器的Draft Environment下的文件;将文件夹下的对应名称csv文件储存为矩阵对象。
print(os.listdir("../input"))
train = pd.read_csv('../input/house-prices-advanced-regression-techniques/train.csv')
test = pd.read_csv('../input/house-prices-advanced-regression-techniques/test.csv')
#显示矩阵对象的维数,核查是否导入成功
print("Train set size:", train.shape)
print("Test set size:", test.shape)
#记录运算开始的时间
print('START data processing', datetime.now(), )
#取出train矩阵(或者称之为“数据帧”dataframe)中title为'Id'的列,赋值给train_ID。所以train_ID是一维列向量了。test_ID类似。
#train_ID和test_ID根本就没有使用,完全可以删除。
#train_ID = train['Id']
#test_ID = test['Id']
##################删除训练集和测试集中的标签列-【开始】#################
#将train矩阵中的'Id'列删除(原地删除,故将inplace设为true),因为原始数据中的数据索引和预测模型的构建没有关系。
#test矩阵类似。
train.drop(['Id'], axis=1, inplace=True)
test.drop(['Id'], axis=1, inplace=True)
##################删除训练集和测试集中的标签列-【结束】#################
###############删除训练集中的极端值和进行数据index更新-【开始】#########
#使用条件筛选操作,通过覆值的方式剔除原始数据train矩阵中的极端值(极端值也被称为outliers),帮助预防房价预测模型出现过拟合。剔除操作也可以视为前剪枝。
train = train[train.GrLivArea < 4500]
#由于删去了部分行,故此时train矩阵中的index列并不连续。使用reset_index命令,在固定非index数据的顺序的前提下(inplace=True),重新对index编号(drop=True)。
train.reset_index(drop=True, inplace=True)
###############删除训练集中的极端值和进行数据index更新-【结束】#########
##########对预测目标数值进行对数变换和特征矩阵对象的创建-【开始】#######
# log1p就是log(1+x),用来对房价数据进行数据预处理,它的好处是转化后的数据更加服从高斯分布,有利于后续的分类结果。
# 需要注意,最后需要将预测出的平滑数据还原,而还原过程就是log1p的逆运算expm1。
train["SalePrice"] = np.log1p(train["SalePrice"])
#单独取出训练数据中的房价列信息,存入y对象。
#y = train.SalePrice.reset_index(drop=True) #.reset_index(drop=True)方法:在原有的索引列重置索引,不再另外添加新列。有必要使用reset_index吗?有必要的,不这样做y将有两套index,作为df的y将有两列。
y = train['SalePrice'].reset_index(drop=True) #对上式的改写
#沿着水平的方向寻找列名为'SalePrice'的列(们),把它们对应的列统统删掉。得到了单纯的特征矩阵,存入train_features对象中。
train_features = train.drop(['SalePrice'], axis=1)
#test本来就没有房价列,所以它本来就是单纯的特征矩阵。
test_features = test
##########对预测目标数值进行对数变换和特征矩阵对象的创建-【结束】#######
##合并训练数据特征矩阵与测试数据特征矩阵,以便统一进行特征处理-【开始】##
#将训练数据中的特征矩阵和测试数据中的特征矩阵合并(.concat[矩阵1,矩阵2]),并对合并后的矩阵index重新编号(.reset_index(drop=True))。
features = pd.concat([train_features, test_features]).reset_index(drop=True)
#检查合并后的矩阵的维数,核查合并结果。
print("剔除训练数据中的极端值后,将其特征矩阵和测试数据中的特征矩阵合并,维度为:",features.shape)
##合并训练数据特征矩阵与测试数据特征矩阵,以便统一进行特征处理-【结束】##
#######################################################数据导入和特征提取-【结束】################################################################################
##############################################################特征处理-【开始】###################################################################################
#对于列名为'MSSubClass'、'YrSold'、'MoSold'的特征列,将列中的数据类型转化为string格式。
features['MSSubClass'] = features['MSSubClass'].apply(str)
features['YrSold'] = features['YrSold'].astype(str)
features['MoSold'] = features['MoSold'].astype(str)
###############################填充空值-【开始】##########################
#按照以下各个特征列的实际情况,依次处理各个特征列中的空值(.fillna()方法)
features['Functional'] = features['Functional'].fillna('Typ') #空值填充为str型数据'Typ'
features['Electrical'] = features['Electrical'].fillna("SBrkr") #空值填充为str型数据"SBrkr"
features['KitchenQual'] = features['KitchenQual'].fillna("TA") #空值填充为str型数据"TA"
features["PoolQC"] = features["PoolQC"].fillna("None") #空值填充为str型数据"None"
#对于列名为'Exterior1st'、'Exterior2nd'、'SaleType'的特征列,使用列中的众数填充空值。
# 1.先查找数据列中的众数:使用df.mode()[]方法
# 解释:df.mode(0或1,0表示对列查找,1表示对行查找)[需要查找众数的df列的index(就是df中的第几列)],将返回数据列中的众数
# 2.使用.fillna()方法进行填充
features['Exterior1st'] = features['Exterior1st'].fillna(features['Exterior1st'].mode()[0])
features['Exterior2nd'] = features['Exterior2nd'].fillna(features['Exterior2nd'].mode()[0])
features['SaleType'] = features['SaleType'].fillna(features['SaleType'].mode()[0])
#对于列名为'GarageYrBlt', 'GarageArea', 'GarageCars'的特征列,使用0填充空值。
for col in ('GarageYrBlt', 'GarageArea', 'GarageCars'):
features[col] = features[col].fillna(0)
#对于列名为'GarageType', 'GarageFinish', 'GarageQual', 'GarageCond'的特征列,使用字符串'None'填充空值。
for col in ['GarageType', 'GarageFinish', 'GarageQual', 'GarageCond']:
features[col] = features[col].fillna('None')
#对于列名为'BsmtQual', 'BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinType2'的特征列,使用字符串'None'填充空值。
for col in ('BsmtQual', 'BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinType2'):
features[col] = features[col].fillna('None')
#聚合函数(按某一列关键字分组)groupby,它的特点是:将返回与传入方法的矩阵维度相同的单个序列。
#transform是与groupby(pandas中最有用的操作之一)通常组合使用,它对传入方法的矩阵进行维度不变的变换。具体变换方法写在括号中,通常会使用匿名函数,对传入矩阵的所有元素进行操作。
#对于features矩阵,按照'MSSubClass'列中的元素分布进行分组,被分组的数据列是'MSZoning'列。feature.groupby(被作为索引的列的名称)[被分组的数据列的名称]
#features.groupby('MSSubClass')['MSZoning']后,得到的是一个以'MSSubClass'为索引,以'MSZoning'为数据列的矩阵。
#.transform()方法将对'MSZoning'数据列进行()内的变换,它将返回和传入矩阵同样维度的矩阵。
#括号内是匿名函数,将对传入矩阵中的空值进行填充,使用的填充元素是传入矩阵中的众数。
features['MSZoning'] = features.groupby('MSSubClass')['MSZoning'].transform(lambda x: x.fillna(x.mode()[0]))
#判断出features矩阵中列为对象的列,将列名存入objects叔祖。对于features矩阵中的各个列对象,将其列中的空值填充为'None'
objects = []
for i in features.columns:
if features[i].dtype == object:
objects.append(i)
features.update(features[objects].fillna('None'))
#使用传入矩阵('LotFrontage'列)的中位数对传入矩阵中的空值进行填充。
#先以'Neighborhood'为标签,以'LotFrontage'为被汇总序列。然后使用被汇总序列中的中位数,对原始矩阵'LotFrontage'列中的空值进行填充。
#transform的特性是同维操作,最后输出结果的顺序和原始数据在序号上完全匹配。
features['LotFrontage'] = features.groupby('Neighborhood')['LotFrontage'].transform(lambda x: x.fillna(x.median()))
#对于整型和浮点型数据列,使用0填充其中的空值。
numeric_dtypes = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64']
numerics = []
for i in features.columns:
if features[i].dtype in numeric_dtypes:
numerics.append(i)
features.update(features[numerics].fillna(0))
###############################填充空值-【结束】##########################
######################数字型数据列偏度校正-【开始】#######################
#使用skew()方法,计算所有整型和浮点型数据列中,数据分布的偏度(skewness)。
#偏度是统计数据分布偏斜方向和程度的度量,是统计数据分布非对称程度的数字特征。亦称偏态、偏态系数。
numeric_dtypes = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64']
numerics2 = []
for i in features.columns:
if features[i].dtype in numeric_dtypes:
numerics2.append(i)
skew_features = features[numerics2].apply(lambda x: skew(x)).sort_values(ascending=False)
#以0.5作为基准,统计偏度超过此数值的高偏度分布数据列,获取这些数据列的index。
high_skew = skew_features[skew_features > 0.5]
skew_index = high_skew.index
#对高偏度数据进行处理,将其转化为正态分布。
#Box和Cox提出的变换可以使线性回归模型满足线性性、独立性、方差齐次以及正态性的同时,又不丢失信息。
for i in skew_index:
features[i] = boxcox1p(features[i], boxcox_normmax(features[i] + 1))#这是boxcox1p的使用方法,参数的具体意义暂时不解释
######################数字型数据列偏度校正-【结束】#######################
######################特征删除和融合创建新特征-【开始】###################
#删除一些特征。df.drop(‘列名’, axis=1)代表将‘列名’对应的列标签(们)沿着水平的方向依次删掉。
features = features.drop(['Utilities', 'Street', 'PoolQC',], axis=1)
#融合多个特征,生成新特征。
features['YrBltAndRemod']=features['YearBuilt']+features['YearRemodAdd']
features['TotalSF']=features['TotalBsmtSF'] + features['1stFlrSF'] + features['2ndFlrSF']
features['Total_sqr_footage'] = (features['BsmtFinSF1'] + features['BsmtFinSF2'] +
features['1stFlrSF'] + features['2ndFlrSF'])
features['Total_Bathrooms'] = (features['FullBath'] + (0.5 * features['HalfBath']) +
features['BsmtFullBath'] + (0.5 * features['BsmtHalfBath']))
features['Total_porch_sf'] = (features['OpenPorchSF'] + features['3SsnPorch'] +
features['EnclosedPorch'] + features['ScreenPorch'] +
features['WoodDeckSF'])
#简化特征。对于某些分布单调(比如100个数据中有99个的数值是0.9,另1个是0.1)的数字型数据列,进行01取值处理。
features['haspool'] = features['PoolArea'].apply(lambda x: 1 if x > 0 else 0)
features['has2ndfloor'] = features['2ndFlrSF'].apply(lambda x: 1 if x > 0 else 0)
features['hasgarage'] = features['GarageArea'].apply(lambda x: 1 if x > 0 else 0)
features['hasbsmt'] = features['TotalBsmtSF'].apply(lambda x: 1 if x > 0 else 0)
features['hasfireplace'] = features['Fireplaces'].apply(lambda x: 1 if x > 0 else 0)
#检查特征处理后,特征矩阵的维数,核查特征处理结果。
print("删除了3个特征,又融合创建了10个新特征,处理之后的特征矩阵维度为:",features.shape)
######################特征删除和融合创建新特征-【结束】###################
####################特征投影、特征矩阵拆解和截取-【开始】#################
#使用.get_dummies()方法对特征矩阵进行类似“坐标投影”操作。获得在新空间下的特征表达。
final_features = pd.get_dummies(features).reset_index(drop=True)
#打印新空间下的特征维数,也是新空间的维数。
print("使用get_dummies()方法“投影”特征矩阵,即分解出更多特征,得到更多列。投影后的特征矩阵维度为:",final_features.shape)
#进行特征空间降阶。截取前len(y)行,存入X阵(因为之前进行了训练数据和测试数据的合并,所以从合并矩阵中取出前len(y)行,就得到了训练数据集的处理后的特征矩阵)。
#截取剩余部分,即从序号为len(y)的行开始,至矩阵结尾的各行,存入X_sub阵。此为完成特征变换后的测试集特征矩阵。
#注:len(df)是行计数方法
X = final_features.iloc[:len(y), :] #y是列向量,存储了训练数据中的房价列信息。截取后得到的X阵的维度是len(y)*(final_features的列数)。
X_sub = final_features.iloc[len(y):, :]#使用len命令,求矩阵X的长度,得到的是矩阵对象的长度,即有矩阵中有多少列,而不是每列上有多少行。
print("删除了3个特征,又融合创建了10个新特征,处理之后的特征矩阵维度为:",'X', X.shape, 'y', y.shape, 'X_sub', X_sub.shape)
#在新生特征空间中,剔除X阵和y阵中有着极端值的各行数据(因为X和y阵在水平方向上是一致的,所以要一起删除同样的行)。outliers数值中给出了极端值的列序号。
#df.drop(df.index[序号])将删除指定序号的各行。再使用=对df覆值。
outliers = [30, 88, 462, 631, 1322]
X = X.drop(X.index[outliers])#因为X阵是经过对特征矩阵进行类似“坐标投影”操作后得到的,列向量y中的行号对应着X阵中的列号。
y = y.drop(y.index[outliers])
####################特征投影、特征矩阵拆解和截取-【结束】#################
######################消除截取后特征矩阵的过拟合-【开始】####################### 这一步的目的是处理X阵和X_sub阵。
#在新生特征空间中,删除将产生过拟合的数据列。
#这种数据列具有如下特征:
overfit = []#用来记录产生过拟合的数据列的序号
for i in X.columns:#遍历截取后特征矩阵的每一列
counts = X[i].value_counts()#使用.value_counts()方法,查看在X矩阵的第i列中,不同的取值分别出现了多少次,默认按次数最高到最低做降序排列。返回一个df。
zeros = counts.iloc[0]#通过行号索引行数据,取出counts列中第一个元素,即出现次数最多的取值到底是出现了多少次,存入zeros
if zeros / len(X) * 100 > 99.94:
#判断某一列是否将产生过拟合的条件:
#截取后的特征矩阵有len(X)列,如果某一列中的某个值出现的次数除以特征矩阵的列数超过99.94%,即其几乎在被投影的各个维度上都有着同样的取值,并不具有“主成分”的性质,则记为过拟合列。
overfit.append(i)
#找到将产生过拟合的数据列的位置后,在特征矩阵中进行删除操作。
overfit = list(overfit)
#overfit.append('MSZoning_C (all)')#这条语句有用吗?是要把训练数据特征矩阵X中的列标签为'MSZoning_C (all)'的列也删除吗?但是训练数据中并没有任何一个列标签名称为MSZoning_C (all)。
X = X.drop(overfit, axis=1)#.copy()#删除截取后特征矩阵X中的过拟合列。因为drop并不影响原数据,所以使用copy。直接覆值应该也可以。
X_sub = X_sub.drop(overfit, axis=1)#.copy()
######################消除截取后特征矩阵的过拟合-【结束】#######################
print("删除极端值及过拟合列后,训练数据特征矩阵的维数为,特征:",'X', X.shape, '对应于特征的对数变换后的房价y', y.shape, '测试数据的特征矩阵(它应该在行、列上未被删减)X_sub', X_sub.shape)
##############################################################特征处理-【结束】###################################################################################
##############################################################机器学习-【开始】###################################################################################
print('特征处理已经完成。开始对训练数据进行机器学习', datetime.now())
#设置k折交叉验证的参数。
kfolds = KFold(n_splits=10, shuffle=True, random_state=42)
#定义均方根对数误差(Root Mean Squared Logarithmic Error ,RMSLE)
def rmsle(y, y_pred):
return np.sqrt(mean_squared_error(y, y_pred))
#创建模型评分函数,根据不同模型的表现打分
#cv表示Cross-validation,交叉验证的意思。
def cv_rmse(model, X=X):
rmse = np.sqrt(-cross_val_score(model, X, y, scoring="neg_mean_squared_error", cv=kfolds))
return (rmse)
#############个体机器学习模型的创建(即模型声明和参数设置)-【开始】############
alphas_alt = [14.5, 14.6, 14.7, 14.8, 14.9, 15, 15.1, 15.2, 15.3, 15.4, 15.5]
alphas2 = [5e-05, 0.0001, 0.0002, 0.0003, 0.0004, 0.0005, 0.0006, 0.0007, 0.0008]
e_alphas = [0.0001, 0.0002, 0.0003, 0.0004, 0.0005, 0.0006, 0.0007]
e_l1ratio = [0.8, 0.85, 0.9, 0.95, 0.99, 1]
#定义ridge岭回归模型(使用二范数作为正则化项。不论是使用一范数还是二范数,正则化项的引入均是为了降低过拟合风险。)
#注:正则化项如果使用二范数,那么对于任何需要寻优的参数值,在寻优终止时,它都无法将某些参数值变为严格的0,尽管某些参数估计值变得非常小以至于可以忽略。即使用二范数会保留变量的所有信息,不会进行类似PCA的变量凸显。
#注:正则化项如果使用一范数,它比L2范数更易于获得“稀疏(sparse)”解,即它的求解结果会有更多的零分量。
ridge = make_pipeline(RobustScaler(), RidgeCV(alphas=alphas_alt, cv=kfolds))
#定义LASSO收缩模型(使用L1范数作为正则化项)(由于对目标函数的求解结果中将得到很多的零分量,它也被称为收缩模型。)
#注:正则化项如果使用二范数,那么对于任何需要寻优的参数值,在寻优终止时,它都无法将某些参数值变为严格的0,尽管某些参数估计值变得非常小以至于可以忽略。即使用二范数会保留变量的所有信息,不会进行类似PCA的变量凸显。
#注:正则化项如果使用一范数,它比L2范数更易于获得“稀疏(sparse)”解,即它的求解结果会有更多的零分量。
lasso = make_pipeline(RobustScaler(), LassoCV(max_iter=1e7, alphas=alphas2, random_state=42, cv=kfolds))
#定义elastic net弹性网络模型(弹性网络实际上是结合了岭回归和lasso的特点,同时使用了L1和L2作为正则化项。)
elasticnet = make_pipeline(RobustScaler(), ElasticNetCV(max_iter=1e7, alphas=e_alphas, cv=kfolds, l1_ratio=e_l1ratio))
#定义SVM支持向量机模型
svr = make_pipeline(RobustScaler(), SVR(C= 20, epsilon= 0.008, gamma=0.0003,))
#定义GB梯度提升模型(展开到一阶导数)
gbr = GradientBoostingRegressor(n_estimators=3000, learning_rate=0.05, max_depth=4, max_features='sqrt', min_samples_leaf=15, min_samples_split=10, loss='huber', random_state =42)
#定义lightgbm模型
lightgbm = LGBMRegressor(objective='regression',
num_leaves=4,
learning_rate=0.01,
n_estimators=5000,
max_bin=200,
bagging_fraction=0.75,
bagging_freq=5,
bagging_seed=7,
feature_fraction=0.2,
feature_fraction_seed=7,
verbose=-1,
#min_data_in_leaf=2,
#min_sum_hessian_in_leaf=11
)
#定义xgboost模型(展开到二阶导数)
xgboost = XGBRegressor(learning_rate=0.01, n_estimators=3460,
max_depth=3, min_child_weight=0,
gamma=0, subsample=0.7,
colsample_bytree=0.7,
objective='reg:linear', nthread=-1,
scale_pos_weight=1, seed=27,
reg_alpha=0.00006)
#############个体机器学习模型的创建(即模型声明和参数设置)-【结束】############
###########################集成多个个体学习器-【开始】##########################
###!!!!!!!!!!!!
###!!!!!!!!!!!!
###!!!regressors=(...)中并没有纳入前面的svr模型,怎么回事?
###!!!!!!!!!!!!
###!!!!!!!!!!!!
stack_gen = StackingCVRegressor(regressors=(ridge, lasso, elasticnet, gbr, xgboost, lightgbm),
meta_regressor=xgboost,
use_features_in_secondary=True)#regressors=(...)中并没有纳入前面的svr模型
###########################集成多个个体学习器-【结束】##########################
############################进行交叉验证打分-【开始】###########################
#进行交叉验证,并对不同模型的表现打分
#(由于是交叉验证,将使用不同的数据集对同一模型进行评分,故每个模型对应一个得分序列。展示模型得分序列的平均分、标准差)
print('进行交叉验证,计算不同模型的得分TEST score on CV')
#打印二范数rideg岭回归模型的得分
score = cv_rmse(ridge)
print("二范数rideg岭回归模型的得分: {:.4f} ({:.4f})\n".format(score.mean(), score.std()), datetime.now(), )
#打印一范数LASSO收缩模型的得分
score = cv_rmse(lasso)
print("一范数LASSO收缩模型的得分: {:.4f} ({:.4f})\n".format(score.mean(), score.std()), datetime.now(), )
#打印elastic net弹性网络模型的得分
score = cv_rmse(elasticnet)
print("elastic net弹性网络模型的得分: {:.4f} ({:.4f})\n".format(score.mean(), score.std()), datetime.now(), )
#打印SVR支持向量机模型的得分
score = cv_rmse(svr)
print("SVR支持向量机模型的得分: {:.4f} ({:.4f})\n".format(score.mean(), score.std()), datetime.now(), )
#打印lightgbm轻梯度提升模型的得分
score = cv_rmse(lightgbm)
print("lightgbm轻梯度提升模型的得分: {:.4f} ({:.4f})\n".format(score.mean(), score.std()), datetime.now(), )
#打印gbr梯度提升回归模型的得分
score = cv_rmse(gbr)
print("gbr梯度提升回归模型的得分: {:.4f} ({:.4f})\n".format(score.mean(), score.std()), datetime.now(), )
#打印xgboost模型的得分
score = cv_rmse(xgboost)
print("xgboost模型的得分: {:.4f} ({:.4f})\n".format(score.mean(), score.std()), datetime.now(), )
############################进行交叉验证打分-【结束】###########################
#########使用训练数据特征矩阵作为输入,训练数据对数处理后的预测房价作为输出,进行各个模型的训练-【开始】#########
#开始集合所有模型,使用stacking方法
print('进行模型参数训练 START Fit')
print(datetime.now(), '对stack_gen集成器模型进行参数训练')
stack_gen_model = stack_gen.fit(np.array(X), np.array(y))
print(datetime.now(), '对elasticnet弹性网络模型进行参数训练')
elastic_model_full_data = elasticnet.fit(X, y)
print(datetime.now(), '对一范数lasso收缩模型进行参数训练')
lasso_model_full_data = lasso.fit(X, y)
print(datetime.now(), '对二范数ridge岭回归模型进行参数训练')
ridge_model_full_data = ridge.fit(X, y)
print(datetime.now(), '对svr支持向量机模型进行参数训练')
svr_model_full_data = svr.fit(X, y)
print(datetime.now(), '对GradientBoosting梯度提升模型进行参数训练')
gbr_model_full_data = gbr.fit(X, y)
print(datetime.now(), '对xgboost二阶梯度提升模型进行参数训练')
xgb_model_full_data = xgboost.fit(X, y)
print(datetime.now(), '对lightgbm轻梯度提升模型进行参数训练')
lgb_model_full_data = lightgbm.fit(X, y)
#########使用训练数据特征矩阵作为输入,训练数据对数处理后的预测房价作为输出,进行各个模型的训练-【结束】#########
############################进行交叉验证打分-【结束】###########################
########定义个体学习器的预测值融合函数,检测预测值融合策略的效果-【开始】#######
#综合多个模型产生的预测值,作为多模型组合学习器的预测值
def blend_models_predict(X):
return ((0.1 * elastic_model_full_data.predict(X)) + \
(0.05 * lasso_model_full_data.predict(X)) + \
(0.1 * ridge_model_full_data.predict(X)) + \
(0.1 * svr_model_full_data.predict(X)) + \
(0.1 * gbr_model_full_data.predict(X)) + \
(0.15 * xgb_model_full_data.predict(X)) + \
(0.1 * lgb_model_full_data.predict(X)) + \
(0.3 * stack_gen_model.predict(np.array(X))))
#打印在上述模型配比下,多模型组合学习器的均方根对数误差(Root Mean Squared Logarithmic Error ,RMSLE)
#使用训练数据对创造的模型进行k折交叉验证,以训练创造出的模型的参数配置。交叉验证训练过程结束后,将得到模型的参数配置。使用得出的参数配置下,在全体训练数据上进行验证,验证模型对全体训练数据重构的误差。
print('融合后的训练模型对原数据重构时的均方根对数误差RMSLE score on train data:')
print(rmsle(y, blend_models_predict(X)))
########定义个体学习器的预测值融合函数,检测预测值融合策略的效果-【结束】#######
########将测试集的特征矩阵作为输入,传入训练好的模型,得出的输出写入.csv文件的第2列-【开始】########
print('使用测试集特征进行房价预测 Predict submission', datetime.now(),)
submission = pd.read_csv("../input/house-prices-advanced-regression-techniques/sample_submission.csv")
#函数注释:.iloc[:,1]是基于索引位来选取数据集,[索引1:索引2],左闭右开。
submission.iloc[:,1] = np.floor(np.expm1(blend_models_predict(X_sub)))
########将测试集的特征矩阵作为输入,传入训练好的模型,得出的输出写入.csv文件的第2列-【结束】########
#---------------------------------------------------------------------------------------------------------------------------#
#---------------------------------------------------------------------------------------------------------------------------#
#---------------------------------------------------------------------------------------------------------------------------#
# 当对平台未公开的测试集进行预测时,前述模型的误差是0.114 this kernel gave a score 0.114
# 为了提高模型的得分,引入其他模型的优秀预测结果,与前述模型的预测结果进行混合(有点类似抄别人的答案,但实质是扩大集成模型的规模,引入更多的模型) let's up it by mixing with the top kernels
######################模型输出结果融合-【开始】#############################
#在多模型集成学习器预测结果的基础上,融合其他优秀模型(即平台上其他均方根对数误差小的模型)的预测结果。
#这步操作是为了降低多模型集成学习器的方差。
print('融合其他优秀模型的预测结果 Blend with Top Kernals submissions', datetime.now(),)
sub_1 = pd.read_csv('../input/top-10-0-10943-stacking-mice-and-brutal-force/House_Prices_submit.csv')
sub_2 = pd.read_csv('../input/hybrid-svm-benchmark-approach-0-11180-lb-top-2/hybrid_solution.csv')
sub_3 = pd.read_csv('../input/lasso-model-for-regression-problem/lasso_sol22_Median.csv')
submission.iloc[:,1] = np.floor((0.25 * np.floor(np.expm1(blend_models_predict(X_sub)))) +
(0.25 * sub_1.iloc[:,1]) +
(0.25 * sub_2.iloc[:,1]) +
(0.25 * sub_3.iloc[:,1]))
######################模型输出结果融合-【结束】#############################
####################融合结果的极端值剔除-【开始】###########################
#处理融合后结果中的极端值。把太大的数值(降序排列时,位于顶部往下0.005的数值,就是只有0.005的数比它大)缩小一点(乘以0.77),把太小的数值(降序排列时,位于顶部往下0.99的数值)放大一点(乘以1.1)
q1 = submission['SalePrice'].quantile(0.005)
q2 = submission['SalePrice'].quantile(0.995)
submission['SalePrice'] = submission['SalePrice'].apply(lambda x: x if x > q1 else x*0.77)
submission['SalePrice'] = submission['SalePrice'].apply(lambda x: x if x < q2 else x*1.1)
####################融合结果的极端值剔除-【结束】###########################
#以csv文件的形式输出预测值
submission.to_csv("House_price_submission.csv", index=False)
print('融合结果.csv文件输出成功 Save submission', datetime.now())
##############################################################机器学习-【结束】###################################################################################