算法:如何理解“栈”
如何理解“栈”?
关于“栈”,有一个非常贴切的例子,就是一摞叠在一起的盘子。我们平时放盘子的时候,都是从下往上一个一个放;取的时候,我们也是从上往下一个一个地依次取,不能从中间任意抽出。后进者先出,先进者后出,这就是典型的“栈”结构。

从栈的操作特性上来看,栈是一种“操作受限”的线性表,只允许在一端插入和删除数据。
问题是,相比数组和链表,栈带给我们的只有限制,并没有任何优势,为什么不直接使用数组或者链表呢?为什么非得用这个“操作受限”的“栈”呢?
- 事实上,从功能上来说,数组和链表确实可以替代栈,但是必须明确的是,特定的数结构是对特定场景的抽象,而且,数组或链表暴露了太多的操作接口,操作上的确灵活自由,但使用时就比较不可控,自然也更容易出错。
- 当某个数据集合只涉及在一端插入和删除数据,并且满足后进先出、先进后出的特性,我们就应该选择“栈”这种数据结构
如何实现一个“栈”
从刚才栈的定义里,我们可以看出,栈主要包含两个操作,入栈和出栈,也就是在栈顶插入一个数据和从栈顶删除一个数据。理解了栈的定义之后,我们来看一看如何用代码实现一个栈。
实际上,栈既可以用数组来实现,也可以用链表来实现。
- 用数组实现的栈,我们叫作顺序栈
- 用链表实现的栈,我们叫作链式栈
下面用java实现了一个数组栈
// 基于数组实现的顺序栈
public class ArrayStack {
private String[] items; // 数组
private int count; // 栈中元素个数
private int n; // 栈的大小
// 初始化数组,申请一个大小为 n 的数组空间
public ArrayStack(int n) {
this.items = new String[n];
this.n = n;
this.count = 0;
}
// 入栈操作
public boolean push(String item) {
// 数组空间不够了,直接返回 false,入栈失败。
if (count == n) return false;
// 将 item 放到下标为 count 的位置,并且 count 加一
items[count] = item;
++count;
return true;
}
// 出栈操作
public String pop() {
// 栈为空,则直接返回 null
if (count == 0) return null;
// 返回下标为 count-1 的数组元素,并且栈中元素个数 count 减一
String tmp = items[count-1];
--count;
return tmp;
}
}
了解了定义和基本操作,那它的操作的时间、空间复杂度是多少呢?
- 不管是顺序栈还是链式栈,我们存储数据只需要一个大小为n的数组就足够了。在入栈和出栈的过程中,只需要一两个临时变量存储空间,所以空间复杂度是O(1)
- 注意,这里存储数据需要一个大小为n的数组,并不是说空间复杂度就是O(n)。因为,这n个空间是必须的,无法省掉。所以我们说空间复杂度的时候,是指除了原本的数据存储空间,算法运行还需要额外的存储空间
- 对于时间复杂度,不管是顺序栈还是链式栈,入栈、出栈只涉及栈顶个别数据的操作,所以时间复杂度也是O(1)
支持动态扩容的顺序栈
上面的数组栈,是一个固定大小的栈,也就是说,在初始化栈的时候需要事先指定栈的大小。当栈满之后,就无法再往栈里添加数据了。尽管链式栈的大小不受限,但要存储next指针,内存消耗相对比较多。那我们如果基于数组实现一个可以支持动态扩容的栈呢?
要实现一个支持动态扩容的栈,我们只需要底层依赖一个支持动态扩容的数组就可以了。。当栈满了之后,我们就申请一个更大的数组,将原来的数据搬移到新数组中。如下:
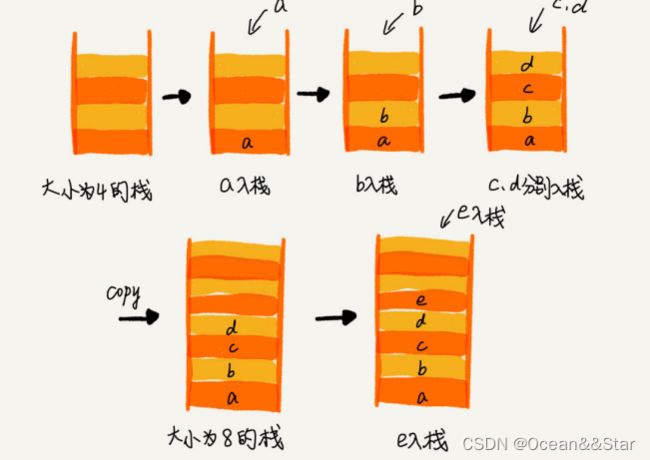
实际上,支持动态扩容的顺序栈,我们平时开发中并不常用到。我们重点来看一下复杂度分析
(1) 对于出栈操作来说,我们不会涉及内存的重新申请和数据的搬移,所以出栈的时间复杂度仍然是O(1)。但是,对于出栈操作来说,当栈中有空闲空间时,入栈操作的时间复杂度是O(1);当空间不够时,就需要重新申请内存和数据搬移,所以时间复杂度就是O(n)
(2)也就是说,对于入栈操作来说,最好情况时间复杂度是O(1),最坏情况时间复杂度就是O(n)。
(3)那平均情况时间复杂度又是多少呢?
为了分析的方便,我们需要事先做一些假设和定义
- 栈空间不够时,我们重新申请一个是原来大小两倍的数组
- 为了简化分析,加入只有入栈操作没有出栈操作
- 定义不涉及内存搬移的入栈操作为 simple-push 操作,时间复杂度为 O(1)。
如果当前栈大小为k,并且已满,当再有新的数据要入栈时,就需要重新申请2倍大小的内存,并且做k个数据的搬移操作,然后再入栈。但是,接下来的k-1次入栈操作,我们都不需要再重新申请内存和搬移数据,所以这k-1次入栈操作都只需要一个 simple-push操作就可以完成。

可以看的出来,这K次入栈操作,总共涉及了K个数据的搬移,以及K次simple-push操作。将k个数据搬移均摊到K次入栈操作,那每个入栈操作只需要一个数据搬移和一个simple-push操作。以此类推,入栈操作的均摊时间复杂度就位O(1)
通过这个例子的实战分析,也印证了均摊时间复杂度一般都等于最好情况时间复杂度这个结论。因为在大部分情况下,入栈操作的时间复杂度O都是O(1),只有在个别时刻才会退化为O(n),所以把耗时多的入栈操作的时间均摊到其他入栈操作上,平均情况下的耗时就会接近O(1)
应用
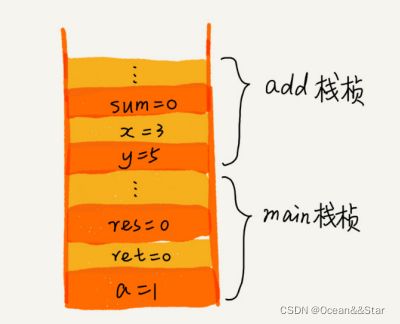
栈在函数调用中的应用
我们知道,操作系统给每个线程分配了一块独立的内存空间,这块内存被组织成“栈”这种结构,用来存储函数调用时的临时变量。每进入一个函数,都会将临时变量作为一个栈帧入栈,当被调用函数执行完成,返回之后,将这个函数对应的栈帧出栈。
看个例子
int main() {
int a = 1;
int ret = 0;
int res = 0;
ret = add(3, 5);
res = a + ret;
printf("%d", res);
reuturn 0;
}
int add(int x, int y) {
int sum = 0;
sum = x + y;
return sum;
}
从代码中我们可以看出,main() 函数调用了 add() 函数,获取计算结果,并且与临时变量a 相加,最后打印 res 的值。在执行到add() 函数时,函数调用栈的情况如下:
为什么函数调用要用“栈”来保存临时变量呢?用其他数据结构不行吗?
- 其实,我们不一定非要用栈来保存临时变量,只不过如果这个函数调用符合后进先出的特性,用栈这种数据结构来实现,是最顺理成章的选择。
- 函数调用之所以用栈,是因为函数调用中经常嵌套,栗子:A调用B,B又调用C,那么就需要先把C执行完,结果赋值给B中的临时变量,B的执行结果再赋值给A的临时变量,嵌套越深的函数越需要被先执行,这样刚好符合栈的特点,因此每次遇到函数调用,只需要压栈,最后依次从栈顶弹出依次执行即可
- 函数调用和返回符合后进先出原则,而局部变量的生命周期应该和函数一致,所以用栈保存局部变量是合适的,函数出栈的时候同时销毁局部变量
编译器如何利用栈来实现表达式求值的
举个例子,对于算术表达式,计算机是怎么计算的呢?
- 实际上,编译器就是通过两个栈来实现的。其中一个保存操作数的栈,另一个是保证运算符的栈。
- 我们从左到右遍历表达式,当遇到数字,我们就直接压入操作数栈;当遇到运算符,就与运算符栈的栈顶元素进行比较
- 如果比运算符栈顶元素的优先级高,就将当前运算符压入栈;如果比运算符栈顶元素的优先级低或者相同,从运算符栈中取栈顶运算符,从操作数栈的栈顶取 2 个操作数,然后进行计算,再把计算完的结果压入操作数栈,继续比较。
比如对于将 3+5*8-6,计算过程如下:
栈在括号匹配中的应用
假设表达式中只包含三种括号,圆括号 ()、方括号 [] 和花括号{},并且它们可以任意嵌套。比如,{[{}]}或 [{()}([])] 等都为合法格式,而{[}()] 或 [({)] 为不合法的格式。那现在给你一个包含三种括号的表达式字符串,如何检查它是否合法呢?
- 这里也可以用栈来解决。我们用栈来保存未匹配的左括号,从左到右依次扫描字符串。
- 当扫描到左括号时,则将其压入栈中;当扫描到右括号时,从栈顶取出一个左括号。
- 如果能够匹配,比如“(”跟“)”匹配,“[”跟“]”匹配,“{”跟“}”匹配,则继续扫描剩下的字符串。如果扫描的过程中,遇到不能配对的右括号,或者栈中没有数据,则说明为非法格式。
- 当所有的括号都扫描完成之后,如果栈为空,则说明字符串为合法格式;否则,说明有未匹配的左括号,为非法格式。
#include 利用栈实现浏览器的前进和后退功能
申请两个栈,X 和 Y,
- 把首次浏览的页面依次压入栈 X
- 当点击后退按钮时,再依次从栈 X 中出栈,并将出栈的数据依次放入栈 Y
- 当点击前进按钮时,我们依次从栈Y 中取出数据,放入栈 X 中
- 当栈 X 中没有数据时,那就说明没有页面可以继续后退浏览了。当栈 Y 中没有数据,那就说明没有页面可以点击前进按钮浏览了。
比如你顺序查看了 a,b,c 三个页面,我们就依次把 a,b,c 压入栈,这个时候,两个栈的数据就是这个样子:
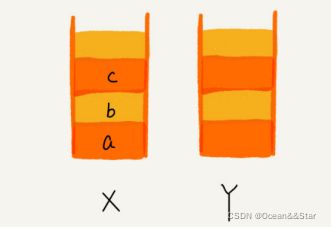
当你通过浏览器的后退按钮,从页面 c 后退到页面 a 之后,我们就依次把 c 和 b 从栈 X 中弹出,并且依次放入到栈 Y。这个时候,两个栈的数据就是这个样子:
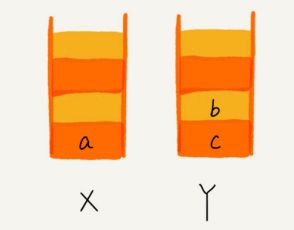
这个时候你又想看页面 b,于是你又点击前进按钮回到 b 页面,我们就把 b 再从栈 Y 中出栈,放入栈 X 中。此时两个栈的数据是这个样子:

这个时候,你通过页面 b 又跳转到新的页面 d 了,页面 c 就无法再通过前进、后退按钮重复查看了,所以需要清空栈 Y。此时两个栈的数据这个样子:
实现栈
golang使用切片实现数组栈(切片使用技巧)
准备
- 切片的头部插入一个元素
slice := []int{1, 2, 3, 4};
value := -1
slice = append([]int{value}, slice...)
- 切片的尾部插入一个元素
slice := []int{1, 2, 3, 4};
value := -1
slice = append(slice, value)
make([]interface{}, 0)和make([]interface{}, 10)的区别,这个对s.values = append(s.values, item)有很大的影响
- 删除第一个元素
slice = slice[1:]
- 删除切片中某个索引的元素:
slice := []int{1, 2, 3, 4};
pos := 2 // 待删除元素的位置
slice = append(slice[:pos], slice[pos + 1:]...)
版本一:容量不受限制的数组栈
stack.go
package main
import "fmt"
type Stack struct {
values []interface{} // 用来存储数据
top int // 栈顶元素索引
}
func NewStack() *Stack {
return &Stack{
values: make([]interface{}, 0),
top: -1,
}
}
// 放置元素
func (s *Stack)Push(item interface{}) {
s.values = append(s.values, item)
s.top++
}
// 获取栈顶元素但是不删除它
func (s *Stack)Peek()(interface{}, error) {
if s.top < 0 {
return nil, fmt.Errorf("[ERR] Index out of range")
}
item := s.values[s.top]
return item, nil
}
// 栈中多少个元素
func (s *Stack)Size() int {
return s.top + 1
}
// 弹出栈顶元素
func (s *Stack) Pop()(interface{}, error) {
if s.top < 0 {
return nil, fmt.Errorf("[ ERR ] Index out of range")
}
item := s.values[s.top]
s.values = append(s.values[:s.top], s.values[s.top + 1:]...)
s.top--
return item, nil
}
stack_test.go
package main
import "testing"
func TestStackPushAndPop(t *testing.T) {
s := NewStack()
s.Push("test_1")
if v, err := s.Pop(); err == nil {
if "test_1" != v && s.top == 0 {
t.Errorf("Failed to Pop")
}
} else {
t.Errorf("Failed to Pop")
}
if s.top != -1 {
t.Errorf("The top should be -1. Instead: %d", s.top)
}
s.Push("test_2")
s.Push("test_3")
if s.top != 1 {
t.Errorf("The top should be 1. Instead: %d", s.top)
}
if v, err := s.Pop(); err == nil {
if "test_3" != v && s.top == 1 {
t.Errorf("Failed to Pop")
}
} else {
t.Errorf("Failed to Pop")
}
}
func TestStackSize(t *testing.T) {
s := NewStack()
if s.Size() != 0 {
t.Errorf("The size of the stack should be 0. Instead %d", s.Size())
}
s.Push("Test")
s.Push("Test_2")
s.Push("Test_3")
if s.Size() != 3 {
t.Errorf("The size of the stack should be 3. Instead %d", s.Size())
}
}
版本二:容量受限的数组栈
package main
import (
"fmt"
)
type StackArray interface {
Push(v interface{}) error
Peek() (interface{}, error)
Pop()(interface{}, error)
Get() []interface{}
Size() int
IsEmpty() bool
Clear()
IsFull() bool //是否满了
}
type Stack struct {
values []interface{} // 用来存储数据
top int // 栈顶元素索引
capacity int // 栈最多能够存放多少元素,默认不限制
}
func NewStack() *Stack{
return &Stack{
values: make([]interface{}, 0),
top: -1,
capacity: -1,
}
}
func NewStackSize(capacity int) *Stack {
return &Stack{
values: make([]interface{}, capacity),
top: -1,
capacity: capacity,
}
}
func (s *Stack) Size() int {
return s.top + 1
}
func (s *Stack) IsEmpty() bool {
return s.top == -1
}
func (s *Stack) IsFull() bool{
if s.capacity == -1 {
return false
}
return s.Size() == s.capacity
}
func (s *Stack)Clear() {
s.top = -1
s.values = []interface{}{}
}
func (s *Stack) Push(v interface{}) error {
if s.IsFull() {
return fmt.Errorf("[ERR] Stack full");
}
//s.values = append(s.values, v) --- error []
s.values[s.top + 1] = v
s.top++;
return nil
}
func (s *Stack) Peek() (interface{}, error) {
if s.IsEmpty() {
return nil, fmt.Errorf("[ERR] Stack is empty")
}
item := s.values[s.top]
return item, nil
}
// 弹出最顶端的数据
func (s *Stack)Pop()(interface{}, error) {
if s.IsEmpty(){
return nil, fmt.Errorf("[ERR] Stack is empty")
}
oldValue := s.values[s.top]
s.values[s.top] = nil
//s.values = append(s.values[:s.top], s.values[s.top + 1:]...)
s.top--
return oldValue, nil
}
// 返回所有压入的数据
func (s *Stack)Get() []interface{} {
return s.values[:s.top + 1]
}
func (s *Stack) SetSize(capacity int) error {
if capacity < 0 {
return fmt.Errorf("capacity must >= 0");
}
s.capacity = capacity
if capacity < s.Size() {
s.values = s.values[:capacity] // 只保留前capacity个元素
s.top = capacity - 1
}
return nil
}
func main() {
//var stack StackArray;
var stack *Stack;
stack = NewStackSize(12)
stack.Push(1)
stack.Push(2)
stack.Push(3)
stack.Push(1)
stack.Push(2)
stack.Push(3)
stack.Push(1)
stack.Push(2)
stack.Push(3)
stack.Push(1)
stack.Push(2)
stack.Push(3)
//stack.Clear()
//fmt.Println(stack.IsFull(), "--------" , stack.Size())
//
//for i := 3; i > 0; i--{
// item, _ := stack.Pop()
//
// fmt.Println(item)
//}
stack.SetSize(3);
fmt.Println(stack.Get())
}
版本三:线程安全、容量不受限制的数组栈
package main
import (
"fmt"
"sync"
)
var errEmptyStack = fmt.Errorf("[ERR], stack is empty\n")
type Stack struct {
stack []interface{}
len int
lock sync.Mutex
}
func NewStack()*Stack {
return &Stack{
stack: make([]interface{}, 0),
len: 0,
lock: sync.Mutex{},
}
}
// 数组头部插入
func (s *Stack)Push(v interface{}) {
s.lock.Lock()
defer s.lock.Unlock()
s.stack = append([]interface{}{v}, s.stack...) // ...是必须的
s.len++
}
func (s *Stack) Peek() (interface{}, error) {
s.lock.Lock()
defer s.lock.Unlock()
if s.len == 0 {
return nil, errEmptyStack
}
return s.stack[0], nil
}
func (s *Stack)Pop() (interface{}, error) {
s.lock.Lock()
defer s.lock.Unlock()
if s.len == 0 {
return nil, errEmptyStack
}
var item interface{}
item, s.stack = s.stack[0], s.stack[1:]
s.len--
return item, nil
}
func (s *Stack)Len() int{
s.lock.Lock()
defer s.lock.Unlock()
return s.len
}
func (s *Stack)Empty() bool{
return s.len == 0
}
测试
package main
import (
"fmt"
"testing"
)
func TestNew(t *testing.T) {
s := NewStack()
if !s.Empty() || s.len != 0 || s.Len() != 0 {
t.Error()
}
s.Push(1)
s.Push(2)
s.Push(3)
if s.stack[0] != 3 ||
s.stack[1] != 2 ||
s.stack[2] != 1 {
fmt.Println(s.stack)
t.Error()
}
if s.Len() != 3 {
t.Error()
}
a, _ := s.Pop()
if a != 3 || s.Len() != 2 {
t.Error()
}
b, _ := s.Peek()
if b != 2 {
t.Error()
}
}
golang实现链式栈
版本一:用哑节点简化操作
- 这个版本是看图说话
package main
import (
"fmt"
)
// 先进先出
type myInterface interface {
Push(data interface{})
Pop() (interface{}, error)
Peek() (interface{}, error)
Clear()
Print()
Empty() bool
}
type node struct {
data interface{}
next *node
}
func newNode(data interface{}) *node {
return &node{
data: data,
next: nil,
}
}
type LinkedStack struct {
top *node
}
func New() *LinkedStack {
return &LinkedStack{
top: newNode(nil),
}
}
func (l *LinkedStack)Empty() bool{
return l.top.next == nil
}
func (l *LinkedStack)Peek() (interface{}, error){
if l.Empty() {
return nil, fmt.Errorf("stack empty");
}
return l.top.next.data, nil
}
func (l *LinkedStack)Push(data interface{}){
if data == nil {
return
}
node := newNode(data)
node.next = l.top.next;
l.top.next = node
}
func (l *LinkedStack) Pop() (interface{}, error){
if l.Empty() {
return nil, fmt.Errorf("stack empty");
}
// 至少有一个
res := l.top.next
l.top.next = l.top.next.next
res.next = nil
return res.data, nil
}
func (l *LinkedStack)Clear(){
l.top.next = nil
}
func (l *LinkedStack)Print(){
curr := l.top.next
for curr != nil{
fmt.Print(curr.data);
fmt.Printf("\t<---\t");
curr = curr.next
}
if peek, err := l.Peek(); err == nil {
fmt.Print("|\t" , peek)
}
fmt.Println()
}
func main(){
ls := New();
for i := 0; i < 10; i++{
ls.Push(i);
}
ls.Print();
for i := 0; i < 12; i++{
_, _ = ls.Pop()
ls.Print();
}
}
版本二:没有哑节点
低质量代码。对于链表节点,无论什么操作,都请用哑节点来简化操作
package main
import "fmt"
type stackItem struct {
item interface{}
next *stackItem
}
type Stack struct {
sp *stackItem
depth int // 元素个数
}
func NewStack() *Stack {
return &Stack{
sp: nil,
depth: 0,
}
}
// 放置元素
func (s *Stack)Push(v interface{}) error {
// 新元素的next指向原来的栈顶元素
item := &stackItem{
item: v,
next: s.sp,
}
// 新元素变成栈顶元素
s.sp = item
s.depth++
return nil
}
// 获取栈顶元素但是不删除它
func (s *Stack)Peek()(interface{}, error) {
if s.depth <= 0 {
return nil, fmt.Errorf("[ ERR ] Stack is empty")
}
return s.sp.item, nil
}
// 栈中多少个元素
func (s *Stack)Size() int {
return s.depth
}
// 弹出栈顶元素
func (s *Stack) Pop()(interface{}, error) {
if s.depth <= 0 {
return nil, fmt.Errorf("[ ERR ] Stack is empty")
}
// 拿到栈顶元素
item := s.sp.item
// 修改栈顶元素
s.sp = s.sp.next
s.depth--
return item, nil
}
func (s *Stack) IsEmpty() bool {
return s.depth == 0
}
测试
func TestStack(t *testing.T) {
var stack *Stack = NewStack()
stack.Push(1)
stack.Push(2)
stack.Push(3)
stack.Push(4)
stack.Push(5)
for i := 5; i > 0; i-- {
item, _ := stack.Pop()
if item != i {
t.Error("TestStack failed...", i)
}
}
}