知识蒸馏论文翻译(7)—— Knowledge Distillation from Internal Representations(内部表征)
知识蒸馏论文翻译(7)—— Knowledge Distillation from Internal Representations(内部表征)
文章目录
-
- 知识蒸馏论文翻译(7)—— Knowledge Distillation from Internal Representations(内部表征)
- 摘要
- 一、介绍
- 二、相关工作
- 三、方法
- 四、实验
- 五、结论
摘要
知识提炼通常是通过训练一个小模型(学生)来模仿一个大而笨重的模型(老师)。其想法是通过使用输出概率作为软标签来优化学生,从而压缩来自教师的知识。然而,当教师人数相当大时,无法保证教师的内部知识会转移到学生身上;即使学生与软标签非常匹配,其内部表现也可能有很大不同。这种内部不匹配可能会破坏原本打算从教师转移到学生身上的泛化能力。在本文中,我们建议将一个大型模型(如BERT)的内部表示提取为它的简化版本。我们制定了两种提取这种表示的方法和各种算法来进行提取。我们对GLUE基准测试中的数据集进行了实验,一致表明,从内部表示中添加知识提取比仅使用软标签提取更有效。
一、介绍
基于Transformer的模型通过在大量任务中建立新的最先进的结果,极大地推进了自然语言处理领域。具体而言,BERT(Devlin等人,2018年)、GPT(Radford等人,2018年)、GPT-2(Radford等人,2019年)、XLM(Lample and Conneau,2019年)、XLNet(Yang等人,2019年)和RoBERTa(Liu等人,2019c)负责文本分类、情感分析、语义角色标记、问答等任务。然而,大多数模型都有数亿个参数,这大大降低了训练过程和推理时间。此外,大量参数需要大量内存消耗,这使得此类模型难以在计算资源严格受限的生产环境中采用。
由于这些限制,已经提出了许多方法来减小模型的大小,同时仍然提供类似的性能。最有效的技术之一是师生环境中的知识提炼(KD)(Hinton、Vinyals和Dean 2015),其中一个笨重的已经优化的模型(即教师)产生输出概率,用于训练简化模型(即学生)。与“one-hot标签”培训不同,在“one-hot标签”培训中,课程是相互排斥的,使用概率分布可以提供有关样本相似性的更多信息,这是师生蒸馏的关键部分。
尽管学生需要的参数较少,但表现仍与老师相似,但最近的研究表明,从巨大的模型中提取信息很困难。Mirzadeh等人(2019年)指出,当教师和学生之间的差距很大时(例如,浅层和深层神经网络),学生很难接近教师。他们建议使用中级助教(TA)模型从教师那里提取信息,然后使用TA模型向学生提取信息。然而,我们认为,大型教师获取的抽象仅通过输出概率暴露,这使得学生很难推断教师(或TA模型)的内部知识。这可能会让学生产生非常不同的内部表征,破坏最初打算从教师那里转移的泛化能力。
在本文中,我们建议将KD应用于内部表示。我们的方法允许学生通过有效地转移其语言属性,在内部表现为教师。我们在老师的不同内部点进行蒸馏,这使学生能够系统地学习和压缩大模型的中间层的蒸馏。通过包含内部表征,我们表明,我们的学生优于其在真实值标签、软标签或两者上训练的同源模型。
二、相关工作
知识提取已成为将大型模型压缩为更简单、更快模型的最有效、最简单的技术之一。该框架的多功能性允许KD扩展到不同任务中的一组专家模型将其知识提取到一个统一的多任务学习网络中的场景(Clark et al.2019b),以及将多任务模型集成到一个特定任务网络中的相反场景(Liu et al.2019a;2019b)。通过将相同的原理应用于内部表示,我们用不同的公式扩展了知识提取框架。
Romero等人(2014)最初探索了使用内部表征来指导学生模型的培训。他们提出了FITNET,这是一个卷积的学生网络,比老师更薄、更深,同时使用的参数也少得多。在他们的工作中,他们在教师和学生模型中建立了一个中点,以比较内部表征。由于教师和学生之间的维度不同,他们使用卷积回归模型将这些向量映射到同一个空间,这增加了大量的学习参数。此外,他们主要关注于提供比教师更深的学生网络,利用卷积网络中深度的特殊优势。我们的工作不同于他们的不同方面:
- 在中间层使用单点损失主要有一个规则化效果,但不能保证从老师那里转移内部知识;
- 我们的蒸馏方法适用于所有学生层,有效地将教师的层组压缩为学生的单层;
- 我们使用内部表示,而不是依赖额外的参数来执行蒸馏;
- 我们不关注比老师更深的模型,因为这会减慢推理时间,而且这不一定是基于变压器的模型的优势。
在这项工作的同时,研究了类似的变压器蒸馏技术。Sanh等人(2019年)提出了DistilBERT,它在训练前对BERT进行压缩,以提供更小的通用模型。他们使用蒙面语言建模损失、隐藏状态下的余弦嵌入损失和师生蒸馏损失对模型进行预训练。相反,Sun等人(2019年)在特定任务的微调过程中,利用隐藏状态的MSE损失和软标签和硬标签的交叉熵损失提取他们的模型。虽然我们的工作与他们的工作相似,但最相关的差异是1)在自我注意概率下使用KL发散损失,这已被证明可以捕获语言知识(Clark等人,2019a),以及2)引入新算法从教师那里提取内部知识(即渐进式和堆叠式知识提取)。
课程学习(CL)(Bengio 2009)是另一个研究方向,通过建立简单的概念来关注复杂任务的教学。虽然目标与我们的类似,但CL是分阶段进行的,首先关注简单的任务,然后逐步转移到更复杂的任务。然而,这种方法需要在初步任务之间进行注释,并且必须仔细挑选这些注释,以便构建任务之间的顺序和关系有助于模型。与CL不同的是,我们专注于教授优化复杂模型的内部表示,假设该模型具有感兴趣任务的初步构建知识。
其他模型压缩技术包括量化(Hubara et al.2017;He et al.2016;Courbariaux et al.2016)和权重修剪(Han、Mao和Dally 2015)。第一种是通过降低每个参数的精度,将大模型近似为小模型。这些宽容侧重于将权重移除到对模型性能没有实质性影响的网络中。这些技术是我们在本文中提出的方法的补充,这可能会导致更有效的整体压缩方法。
三、方法
在本节中,我们将详细介绍从内部表示中提取知识的过程。首先,我们描述了标准KD框架(Hinton、Vinyals和Dean 2015),这是我们方法的重要组成部分。然后,我们将目标函数形式化,以提取基于变压器的模型的内部知识。最后,我们提出了各种算法来进行内部蒸馏过程。
知识蒸馏:Hinton、Vinyals和Dean(2015)提出了知识蒸馏(KD)作为一个框架,将一个大型模型压缩为一个简化模型,以获得类似的结果。该框架使用教师-学生设置,学生从教师提供的真实值标签(如果可用)和软标签中学习。与软标签中每个类相关的概率质量允许学生了解关于给定样本标签相似性的更多信息。考虑软标签和硬标签的KD公式如下所示:
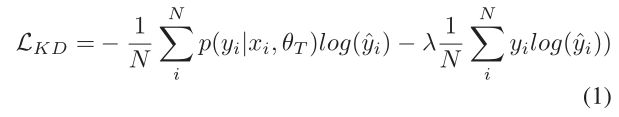
其中 θ T \theta_T θT表示教师的参数, p ( y i ∣ x i , θ T ) p(y_i|x_i,\theta_T) p(yi∣xi,θT)是其软标签; y ^ i \hat{y}_i y^i是由 p ( y i ∣ x i , θ S ) p(y_i|x_i,\theta_S) p(yi∣xi,θS)给出的学生预测,其中 θ S \theta_S θS表示其参数, λ \lambda λ是一个小的标量,用于加权硬标签损失。由于软标签通常呈现高熵,梯度往往比硬标签的梯度小。因此, λ \lambda λ通过减少硬损失的影响来平衡术语。
匹配内部表示:为了使学生模型表现为教师模型,通过教师输出的软标签对学生进行优化。此外,学生还通过匹配其内部表示来获得隐藏在教师中的抽象。也就是说,我们希望通过将教师的多层知识压缩为学生的单层知识,来教会学生如何在内部行为。图1显示了一个教师的层数是学生的两倍,其中彩色框表示学生被教授教师内部表示的层。在这种情况下,学生将两层压缩为一层,同时保留跨教师层的语言行为。
我们研究了基于变压器模型的内部KD,特别是BERT和简化版本(即更少的变压器层)的情况。我们使用损失函数中的两个项来定义内部KD。给定一对要匹配的变压器层(见图1),我们计算(1)所有变压器头1的自我注意概率的Kullback-Leibler(KL)发散损失,以及(2)给定层的[CLS]激活向量之间的余弦相似性损失。

图1:从内部表示中提取知识。我们展示了教师(左)提取到学生(右)中的内部层。
KL发散损失:考虑 A A A作为自关注矩阵,它包含由 A = s o f t m a x ( d a 0.5 Q K T ) A=softmax(d^{0.5}_aQK^T) A=softmax(da0.5QKT)给出的序列中每个令牌的行概率分布(Vaswani等人,2017年)。对于变压器层中的给定磁头,我们使用KL发散损耗,如下所示:

其中 L L L是序列的长度, A T i A_{T_i} ATi和 A S i A_{S_i} ASi分别描述教师和学生的自我注意矩阵的第i行。将这种损失函数应用于自我注意矩阵的动机来自最近的研究,该研究记录了伯特的注意概率所捕获的语言模式(Clark等人,2019a)。强迫自我注意概率分布之间的差异尽可能小,可以保留学生的语言行为。
余弦相似性损失:对于内部蒸馏损失的第二项,我们使用余弦相似性,如下所示:
![]()
其中, h T h_T hT和 h S h_S hS分别是教师和学生[CLS]标记的隐藏向量表示。我们将这个术语包含在我们的内部 K D KD KD公式中,考虑在通过网络的激活中类似的行为。也就是说,尽管 K L KL KL散度关注于自我关注矩阵,但最终传递到上层的是加权隐藏向量,而不是概率。即使我们强迫自我注意概率相似,也不能保证传递给上层的最终激活是相似的。因此,使用这个额外的术语,我们可以将样本的上下文表示规范化,使其与教师的上下文表示相似。

如何提取内部知识?
教师的不同层面捕捉到不同的语言概念。最近的研究表明,当我们从网络的底部向顶部移动时,伯特构建的语言属性变得更加复杂(Clark et al.2019a)。由于模型建立在底部表示的基础上,除了同时蒸馏所有内部层,我们还考虑蒸馏知识逐步匹配自下而上的内部表示。更具体地说,我们考虑以下情景:
(1)所有层的内部蒸馏。学生的所有层次都经过优化,以匹配每个时代老师的层次。在图1中,蒸馏同时发生在圆圈数字1、2、3和4上。
(2)渐进式内部蒸馏(PID)。我们首先从底层(接近输入)提取知识,然后逐步移动到上层,直到模型只关注分类提取。一次只优化一层。在图1中,损失将由1→2→3→4过渡产生。
(3)堆叠内部蒸馏(SID)。我们首先从较低的层中提取知识,但不是专门从一层移动到另一层,而是在移动到顶层时将前一层产生的损失进行叠加。到达顶端后,我们只执行分类(参见算法1)。在图1中,损耗由1→1+2→1+2+3→4过渡产生。
对于最后两个场景,要移动到上层,学生要么达到每层有限的历元数,要么达到余弦损失阈值,不管先发生什么(参见算法1中的第24行)。此外,这两种情况可以随时与分类损失相结合,而不仅仅是在模型到达顶层之前。