一起学数据结构(10)——排序
从本文开始,通过若干篇文章展开对于数据结构中——排序的介绍。
1. 排序的概念:
将一堆杂乱无章的数据,通过一定的规律顺序排列起来。即将一个无序序列排列成一个有序序(由小到大或者由大到小)的运算。
在数据的排序中需要注意,如果需要排序的对象同时有多个数据域(例如对学生进行排序,往往有学号,班级等多个数据域),排序往往是针对于其中一个数据域进行的。
2. 排序的种类:
对于排序,本文及下面的文章中将着重介绍下列给出的排序:插入排序、希尔排序、选择排序、冒泡排序、快速排序、归并排序、计数排序。
3. 插入排序:
3.1 思路分析:
对于插入排序,其基本思想可以概括为:每一步都将待排序的对象,按照该对象与已有数据的大小关系,插入到前面已经排好序的一组数据的合适的位置中。因此,插入排序可以看作一个一边进行插入,一边保持已有序列有序的排序。
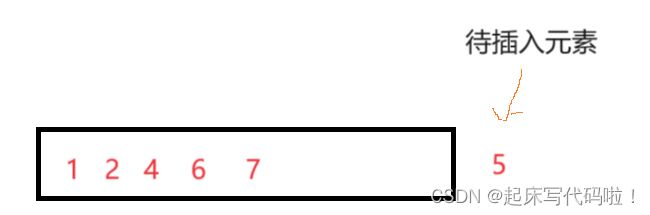
为了便于理解插入排序的基本思想,下面给出一个例子:
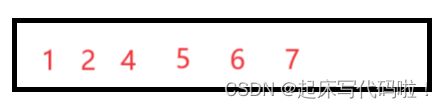
对于上面给出的例子,按照上面插入排序的基本思想来进行排序,则需要首先比较待插入元素![]() 与数组中已有元素进行比较。直到插入到一个合适的位置。所以对上述的案例进行排序后,最终结果为;
与数组中已有元素进行比较。直到插入到一个合适的位置。所以对上述的案例进行排序后,最终结果为;
对于上面给出的插入排序的过程需要理解,并不是真的对数组不断插入新的元素进行排序。而是将数组中的一部分看作插入的部分,例如对于下面的数组:
将已经有序的序列,即数组中的![]() 称为有序序列。将后面的数组成的序列称之为无序序列。如果这个序列进行插入排序,只是将元素
称为有序序列。将后面的数组成的序列称之为无序序列。如果这个序列进行插入排序,只是将元素![]() 看作待插入元素。通过不断比对待插入元素与数组中元素的大小关系,来调整元素
看作待插入元素。通过不断比对待插入元素与数组中元素的大小关系,来调整元素![]() 至合适的位置。
至合适的位置。
为了方便后续编写插入排序的代码,将有序序列的最后一位的下标记为![]() ,将待插入元素的下标记为
,将待插入元素的下标记为![]() 。所以,
。所以,![]() 一开始所对应的下标就是数组第一个元素的下标,即
一开始所对应的下标就是数组第一个元素的下标,即![]() ,待插入元素的下标就是
,待插入元素的下标就是![]() ,即数组中的第二个元素。对比调整后,数组中前两个元素会变为有序序列。接着按照上面的步骤循环,即令
,即数组中的第二个元素。对比调整后,数组中前两个元素会变为有序序列。接着按照上面的步骤循环,即令![]() ,即有序序列的第二个元素,或者说数组中的第一个元素。待插入元素的下标等于
,即有序序列的第二个元素,或者说数组中的第一个元素。待插入元素的下标等于![]() ,即数组中的第二个元素。。。。。。。
,即数组中的第二个元素。。。。。。。
3.2 代码演示:
通过上面给出的思路,可以总结出下面代码:
void InsertSort(int* a, int n)
{
int end = 0;
for (end = 0; end < n - 1; end++)
{
int tmp = a[end + 1];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + 1] = a[end];
}
else
{
break;
}
end--;
}
a[end + 1] = tmp;
}
}对于插入排序,因为没有开辟额外的空间,所以插入排序的空间复杂度为![]() ,当数组完全逆序时,插入排序需要执行的次数可以看作一个等差数列,所以插入排序的时间复杂度为
,当数组完全逆序时,插入排序需要执行的次数可以看作一个等差数列,所以插入排序的时间复杂度为![]()
3.3 插入排序测试:
测试函数如下:
void TestInsertsort()
{
int a[] = { 2,1,3,4,6,9,5,8 };
int size = sizeof(a) / sizeof(int);
InsertSort(a, size);
ArrayPrint(a, size);
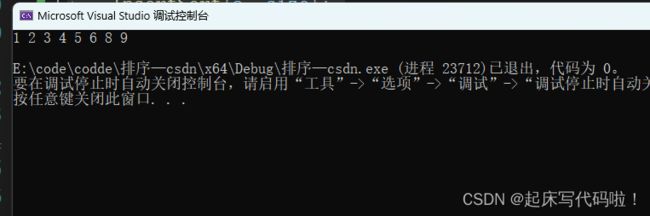
}其中函数![]() 是用于打印数组的函数,原理过于简单,不予解释,运行效果如下:
是用于打印数组的函数,原理过于简单,不予解释,运行效果如下:
4. 希尔排序:
4.1 思路分析及代码演示:
对于上面给出的插入排序中提到,如果插入排序需要排序的数组是逆序的,则插入排序的时间复杂度为![]() ,如果需要排序的数组为顺序的,则时间复杂度为
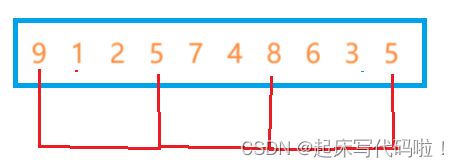
,如果需要排序的数组为顺序的,则时间复杂度为![]() ,为了优化插入排序在排序逆序数组时较大的时间复杂度,可以尝试在对数组进行插入排序之间,先对数组进行依次预排序,让数组中某些元素是顺序的。对于先进行预处理,再进行一次插入排序的排序,就是文章本部分要介绍的希尔排序。例如下面的数组:
,为了优化插入排序在排序逆序数组时较大的时间复杂度,可以尝试在对数组进行插入排序之间,先对数组进行依次预排序,让数组中某些元素是顺序的。对于先进行预处理,再进行一次插入排序的排序,就是文章本部分要介绍的希尔排序。例如下面的数组:
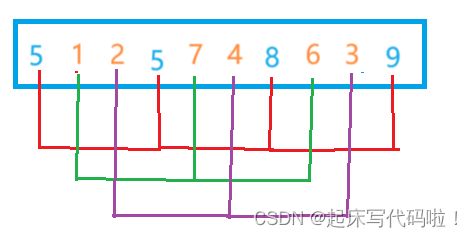
对于预排序,其步骤如下:首先确定一个间隔数,这里将这个间隔数命名为![]() ,通过利用
,通过利用 ![]() 将数组分为若干个区间。并且对相邻区间的首元素进行一次类插入排序的操作。具体步骤将通过下面的图形进行演示:
将数组分为若干个区间。并且对相邻区间的首元素进行一次类插入排序的操作。具体步骤将通过下面的图形进行演示:
1. 假设![]() ,则利用
,则利用![]() 分组后的数组可以表示为:
分组后的数组可以表示为:
继续利用上面方法对数组中未分组的元素进行分组,可以表示为下面的图片,图中不同颜色的图形用于区分不同的组:
2. 接着,对于一组中的元素进行一次类插入排序的操作,即比较同一组的不同区间的首元素的大小关系,将小的元素放到前面。例如,对于红线组中的元素进行上述操作:
对于本部分的操作,可以利用插入排序的思想来实现,依旧定义![]() 表示本组第一个元素的下标,例如红线组的
表示本组第一个元素的下标,例如红线组的![]() ,
,![]() 则表示本组下一个区间的首元素的坐标,再创建一个变量
则表示本组下一个区间的首元素的坐标,再创建一个变量![]() 用于存储
用于存储![]() 所对应的元素。例如红线组的
所对应的元素。例如红线组的![]() 。由于
。由于![]() 所对应的元素>
所对应的元素>![]() 所对应的元素。所以让
所对应的元素。所以让![]() 代表的元素覆盖到
代表的元素覆盖到![]() 的位置。再让
的位置。再让![]() 覆盖到
覆盖到![]() 位置。该过程可用代码表示为:
位置。该过程可用代码表示为:
void ShellSort(int* a, int n)
{
int end = 0;
int gab = 3;
int tmp = a[end + gab];
if (a[end] > tmp)
{
a[end + gab] = a[end];
}
a[end] = tmp;
}但是,上面的过程并不完整,并且只能交换一次,加入遇到下面的情景:
假设 ![]() 所对应的元素为
所对应的元素为![]() ,
,![]() 所对应的元素为
所对应的元素为![]() ,按照上面的代码交换一次后:
,按照上面的代码交换一次后:
可以看到,![]() 这两个元素的大小关系还是不满足。因此,并不能向上面仅仅对
这两个元素的大小关系还是不满足。因此,并不能向上面仅仅对 ![]() ,
,![]() 的元素的大小关系进行判断,还需要对交换后前面的元素的关系重新进行一次判断,如果不满足则再次交换。方法为:再进行一次交换后,令
的元素的大小关系进行判断,还需要对交换后前面的元素的关系重新进行一次判断,如果不满足则再次交换。方法为:再进行一次交换后,令![]() ,此时
,此时![]() 对应的元素为
对应的元素为![]() ,
,![]() 对应的元素为
对应的元素为![]() ,对二者再次进行一次交换。
,对二者再次进行一次交换。
为了满足多次交换的目的需要利用到循环。所以对于循环的结束条件有两条:1是![]() ,2是元素的大小关系不符合。
,2是元素的大小关系不符合。
即使在加上上面的补充后,代码也只能用于单个组中一组![]() ,
,![]() 元素的交换,为了完成整租的交换,需要让
元素的交换,为了完成整租的交换,需要让![]() 所对应的下标不断向后
所对应的下标不断向后![]() 个位置。所以可以将上述代码优化为:
个位置。所以可以将上述代码优化为:
//希尔排序
void ShellSort(int* a, int n)
{
int gab = 3;
for (int end = 0; end < n - gab; end += gab)
{
int tmp = a[end + gab];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gab] = a[end];
end -= gab;
}
else
{
break;
}
}
a[end + gab] = tmp;
}
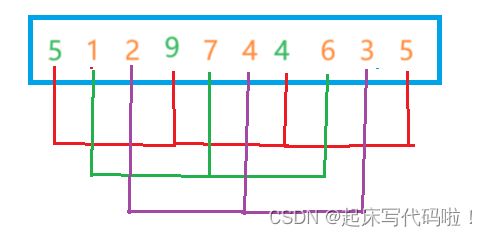
}完善后的代码,可以一次性完成一组的预排序。但是在预排序的过程中需要对多组数据进行排序。通过对下面图形的观察可以得知,当![]() 初始值就为
初始值就为![]() 时,此时进行预排序的就是紫色线条对应的组,也就是需要预排序的最后一组。所以,可以在将上面的代码进行一次优化,让其能够处理多组预排序
时,此时进行预排序的就是紫色线条对应的组,也就是需要预排序的最后一组。所以,可以在将上面的代码进行一次优化,让其能够处理多组预排序
并且,对于![]() 的值也是变化的,
的值也是变化的,![]() 的值越大,数组中大的元素向后移动的距离越长,
的值越大,数组中大的元素向后移动的距离越长,![]() 越小,移动的距离也越小,当
越小,移动的距离也越小,当![]() ,数组为有序。
,数组为有序。
代码如下:
//希尔排序
void ShellSort(int* a, int n)
{
int gab = n;
while (gab > 1)
{
gab = gab / 2;
for (int i = 0; i < gab; i++)
{
for (int end = i; end < n - gab; end += gab)
{
int tmp = a[end + gab];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gab] = a[end];
end -= gab;
}
else
{
break;
}
}
a[end + gab] = tmp;
}
}
}
}对于预排序部分的代码,还有另一种更简洁的部分,这里先给出相应代码,再进行逻辑分析:
//希尔排序
void ShellSort1(int* a, int n)
{
int gab = n;
while (gab > 1)
{
gab = gab / 2;
for (int i = 0; i < n - gab; i++)
{
int end = i;
int tmp = a[end + gab];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gab] = a[end];
end -= gab;
}
else
{
break;
}
}
a[end + gab] = tmp;
}
}
}观察上面给出的代码,可以发现,相对于上面给出的预排序,这种预排序省略了一个![]() 循环。逻辑也不同。对于现在给出的预排序,并不是按照严格分组,先进行完一组,再进行一组。而是在确定了
循环。逻辑也不同。对于现在给出的预排序,并不是按照严格分组,先进行完一组,再进行一组。而是在确定了![]() 之后,直接按照数组下标的顺序进行预排序,例如:
之后,直接按照数组下标的顺序进行预排序,例如:
对于前面一种的预排序,是先对![]() 进行预排序,再对
进行预排序,再对![]() 进行预排序,再对
进行预排序,再对![]() 进行预排序,此时,红线所对应的组完成了预排序,于是再对绿线所对应的组的元素开始预排序,顺序为:
进行预排序,此时,红线所对应的组完成了预排序,于是再对绿线所对应的组的元素开始预排序,顺序为:![]() ,
,![]() 。
。
但是对于现在给出的预排序,预排序的顺序为:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,。。。。。。
,。。。。。。
由于希尔排序的时间复杂度的计算极其复杂,这里直接给出结论,希尔排序的时间复杂度大致在![]() 左右。空间复杂度为
左右。空间复杂度为![]() 。
。
4.2 希尔排序测试:
测试函数如下:
void TestShellSort()
{
int b[] = { 9,1,2,5,7,4,8,6,3,5 };
int size = sizeof(b) / sizeof(int);
ShellSort(b, size);
printf("希尔排序:");
ArrayPrint(b, size);
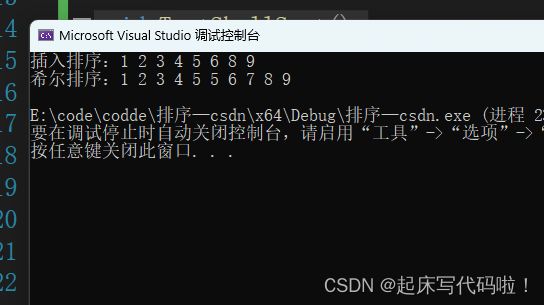
}结果如下:
5. 冒泡排序:
5.1 代码演示:
对于冒泡排序的相关原理,可以在文章C语言——冒泡排序和qsort排序-CSDN博客浏览,文章在本部分只给出冒泡排序的相关代码以及测试结果,对实现原理不做论述。
void BubbleSort(int* a, int n)
{
for (int j = 0; j < n; j++)
{
int exchange = 0;
for (int i = 1; i < n; i++)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
{
break;
}
}
}5.2 冒泡排序测试:
测试函数如下:
//冒泡排序
void BubbleSort(int* a, int n)
{
for (int j = 0; j < n; j++)
{
int exchange = 0;
for (int i = 1; i < n; i++)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
{
break;
}
}
}void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}结果如下:
6. 堆排序 :
对于堆排序的相关原理及代码实现,在之前的文章如何利用堆来模拟堆排序-CSDN博客已经做了详细的解释,这里不再进行多余论述。
7. 选择排序:
7.1 思路分析以及代码演示:
对于选择排序的原理,总结下来只有一句话,即每次排序时,选出数组中最小的值以及最大的值,将最小的值换到数组的最左边,最大的值换到数组的最右边。
为了达成上述目的,可以创建![]() 两个变量,通过遍历数组将二者选择出来,再通过交换函数,让两个值在数组中的位置分别达到最左边,最右边。
两个变量,通过遍历数组将二者选择出来,再通过交换函数,让两个值在数组中的位置分别达到最左边,最右边。
代码如下:
void SelectSort(int* a, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
int mini = begin, maxi = begin;
for (int i = begin + 1; i <= end; i++)
{
if (a[i] > a[maxi])
{
maxi = i;
}
if (a[i] < a[mini])
{
mini = i;
}
}
Swap(&a[begin], &a[mini]);
if (maxi == begin)
{
maxi = mini;
}
Swap(&a[end], &a[maxi]);
begin++;
end--;
}
}7.2 选择排序测试:
测试函数如下:
TestSelectSort()
{
int d[] = { 7,8,1,4,5,9,2,3,6};
int size = sizeof(d) / sizeof(int);
SelectSort(d, size);
printf("选择排序:");
ArrayPrint(d, size);
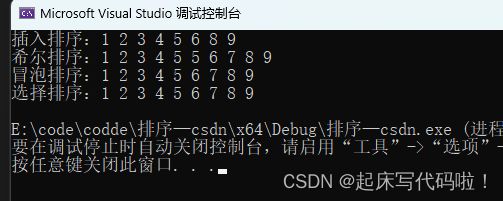
}结果如下:
对于选择排序,显而易见,时间复杂度为![]() ,空间复杂度为
,空间复杂度为![]() 。
。