【刷题篇】回溯算法（深度优先搜索（二））

岛屿数量

给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。
岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外，你可以假设该网格的四条边均被水包围。

class Solution {
public:
    int num=0;
    int next[4][2]={{1,0},{-1,0},{0,-1},{0,1}};
public:
    void findisland(vector<vector<char>>& grid,int row,int col,vector<vector<int>>& sign,int nowr,int nowc)
    {
        if(grid[nowr][nowc]=='1'&&sign[nowr][nowc]==0)
        {
            sign[nowr][nowc]=1;
            for(int i=0;i<4;i++)
            {    
                int newsr=nowr+next[i][0];
                int newsc=nowc+next[i][1];
                //防止越界
                if(newsr>=row||newsr<0||newsc>=col||newsc<0)
                    continue;
                findisland(grid,row,col,sign,newsr,newsc);
            }
        }
    }
    int numIslands(vector<vector<char>>& grid) {
        if(grid.empty())
            return 0;
        int row=grid.size();
        int col=grid[0].size();
        //创建标记数组，防止重复访问
        vector<vector<int>> sign(row,vector<int>(col,0));
        for(int i=0;i<row;i++)
        {
            for(int j=0;j<col;j++)
            {    //要确保他是岛屿并且没有被标记过，才会继续访问，来怎加岛屿数量
                if(grid[i][j]=='1'&&sign[i][j]==0)
                {
                    findisland(grid,row,col,sign,i,j);
                    num++; 
                }
            }
        }
        return num;
    }
};

电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

map<char,string> numMap={{'2',"abc"},{'3',"def"},{'4',"ghi"},{'5',"jkl"},{'6',"mno"},{'7',"pqrs"},{'8',"tuv"},{'9',"wxyz"}};
class Solution {
public:
    void DFS(string & digit,vector<string>& allRet,string curStr,int digitIdx)
    {
        //放入数组
        if(digitIdx==digit.size())
        {
            allRet.push_back(curStr);
            return;
        }
        //获取数字对应的字符映射
        string strMap=numMap[digit[digitIdx]];
        for(char e: strMap)
        {
            DFS(digit,allRet,curStr+e,digitIdx+1);
        }
    }

    vector<string> letterCombinations(string digits) {
        vector<string> vec;
        if(digits.empty())
        {
            return vec;
        }
        DFS(digits,vec,"",0);
        return vec;
    }
};

组合总和

给定一个无重复元素的正整数数组 candidates 和一个正整数 target ，找出 candidates 中所有可以使数字和为目标数 target 的唯一组合。
candidates 中的数字可以无限制重复被选取。如果至少一个所选数字数量不同，则两种组合是不同的。
对于给定的输入，保证和为 target 的唯一组合数少于 150 个。

class Solution {
public:
    void DFS(vector<int>& candidates,vector<vector<int>>& allsum,vector<int>& cursum, int target,int sum,int prev)
    {
        if(sum>=target)
        {
            if(sum==target)
            {//相等的话就插入最终的数组
                allsum.push_back(cursum);
            }
            //只大于的话就返回并pop出一个数据
            return;
        }
        for(int i=prev;i<candidates.size();i++)
        {//插入临时数组进行保存
            cursum.push_back(candidates[i]);
            DFS(candidates,allsum,cursum,target,sum+candidates[i],i);
            cursum.pop_back();//回溯
        }
    }
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        //用来存放最终返回的结果，
        vector<vector<int>> allsum;
        //用来记录临时储存的结果
        vector<int> cursum;
        //记录数据大小与target的比较
        int sum=0;
        //DFS当中的prev也就是0的作用是用来控制循环
        DFS(candidates,allsum,cursum,target,sum,0);
        return allsum;
    }
};

活字印刷

你有一套活字字模 tiles，其中每个字模上都刻有一个字母 tiles[i]。返回你可以印出的非空字母序列的数目。
注意：本题中，每个活字字模只能使用一次。

class Solution {
public:
    void DFS(string& tiles,string curstr,unordered_set<string>& allret,vector<int>& book)
    {
        if(!curstr.empty())
        {
            allret.insert(curstr);
        }
        for(int i=0;i<tiles.size();i++)
        {
            if(book[i]==0)
            {
                book[i]=1;
                DFS(tiles,curstr+tiles[i],allret,book);
                book[i]=0;//回溯
            }
        }
    }
    int numTilePossibilities(string tiles) {
        if(tiles.empty())
        {
            return 0;
        }
        //使用它也已去重
        unordered_set<string> allret;
        //标记，回溯
        vector<int> book(tiles.size(),0);
        //临时
        string curstr;
        DFS(tiles,curstr,allret,book);
        return allret.size();
    }
};

N皇后

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。
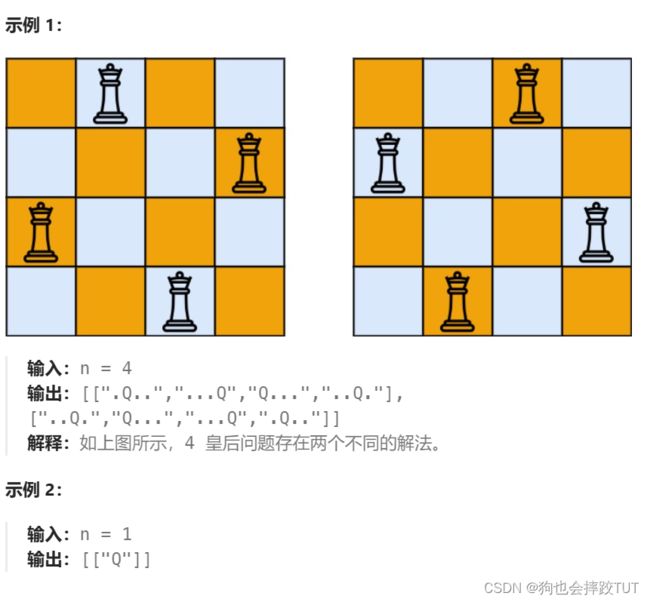
给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

class Solution {
public:
    void DFS(vector<vector<pair<int,int>>>& allsign,vector<pair<int,int>>& partsign,int partRow,int n)
    {
        //下面表示没有冲突，存入数组当中
        if(partRow==n)
        {
            allsign.push_back(partsign);
            return;
        }
        //判断是否有冲突并且遍历回溯
        for(int i=0;i<n;i++)
        {
            //判断是否冲突
            if(isconflict(partsign,partRow,i))
            {
                partsign.push_back(make_pair(partRow,i));
                //换行
                DFS(allsign,partsign,partRow+1,n);
                //回溯
                partsign.pop_back();
            }
        }
    }

    bool isconflict(vector<pair<int,int>>& partsign,int Row,int Col)
    {
        for(pair<int,int> pos : partsign)
        {   //判断是否冲突的条件是在不能在同一列，在一条斜线上不行
            if(pos.second==Col || pos.first+pos.second == Row+Col || pos.first-pos.second == Row-Col )
            {
                return false;
            }
        }
        return true;
    }

    //将标记映射为皇后
    vector<vector<string>> Mapping(vector<vector<pair<int,int>>>& allsign,int n)
    {
        vector<vector<string>> allmat;
        for(vector<pair<int,int>> partsign : allsign)
        {
            //一种排放方式
            vector<string> partmat(n,string(n,'.'));
            for(pair<int,int> pos: partsign)
            {   //替换
                partmat[pos.first][pos.second]='Q';
            }
            allmat.push_back(partmat);
        }
        return allmat;
    }
    vector<vector<string>> solveNQueens(int n) {
        vector<vector<pair<int,int>>> allsign;
        vector<pair<int,int>> partsign;
        DFS(allsign,partsign,0,n);
        return Mapping(allsign,n);
    }
};