2-SAT问题合集-ybtoj

所谓2-SAT问题，就是有两个SAT的问题（误

SAT 是适定性（Satisfiability）问题的简称。一般形式为 k - 适定性问题，简称 k-SAT。而当 $k>2$ 时该问题为 NP 完全的。所以我们只研究k = 1 $k>2$ 的情况。

一、2-SAT问题的定义：

2-SAT，简单的说就是给出 $n$ 个集合，每个集合有两个元素，已知若干个 $<a,b>$，表示 $a$ 与 $b$ 矛盾（其中 $a$与 $b$ 属于不同的集合）。然后从每个集合选择一个元素，判断能否一共选 $n$个两两不矛盾的元素。显然可能有多种选择方案，一般题中只需要求出一种即可。

简单地说：给出 $n$ 个集合，每个集合有 $2$ 个元素，
给出 $m$ 个式子表示不同集合的元素间的关系，要求从 $n$ 个集合中，在每个集合中选取一个元素，形成一个新的集合，该集合满足上述 $m$ 个式子所表述的情况。

(甚至可以简单地理解为有$n$个元素，每个元素有两种取值，给出$m$个限制条件，求合法的$n$的取值集合。)

当然，给问题存在有多个解、有唯一解、无解这三种情况。

二、2-SAT问题的解决：

先给出引例：一个经典的2-SAT问题

有 $n$ 个元素，每个元素可以取 $0$ 或 $1$,给出$m$个限制条件，判断是否有解，如果有解，请求出任意一组合法的解。

（一）如何建立模型：

<1>点的建立

显然这个问题和差分约束有着相似之处，而图论的本质就是表示两个点之间的关系，因此很容易想到将每个元素的两种取值分别看作一个点，将$m$个限制条件看作在不同的点之间建立边的关系，建立一张 有向图（一般情况下都有环）。

具体地说，在2-SAT的建模中，将第 $i$ 个元素拆分成点$i$和点$i+n$,点$i$表示第$i$个元素取$1$，点$i+n$表示第$i$个元素取$0$。
(这个没有特殊要求，按个人习惯即可)

<2>边的建立

每一条有向边，从点$a$指向点$b$,表示当点a所代表的元素选择点a所代表的取值时，点b所代表的元素必须选择点b所代表的取值。
（我的表述能力有限。。可能说的有一些奇怪就是了）

再举一个例子就更好理解了。

现有一个限制条件：
对于元素a和元素b，至少有一个取值为1

那么分类讨论一下：
<1>当$a=0$时，必有$b=1$,因此建边$<a+n,b>$，即$a$取$0$时，$b$必须取$1$.
<2>当$a=1$时，$b$取$0$或$1$均可。
注意：由于建边强调地是表述一定成立的条件，因此对于不确定的取值不能建边，即不确定$a=1$时$b$取什么值，那么就不建边
<3>当$b=0$时,必有$a=1$,因此建边$<b+n,a>$
<4>当$b=1$时，$a$的取值任意，故不建边。

理解了上文所有的表述和引例之后，相信你对2-SAT所处理的问题情景和建模方式已经有了最基本的了解~~

(二）求解2-SAT问题的算法：Tarjan

先回顾一下我们需要解决什么问题：

需要解决的问题分为两类，一类是 判断是否有解 ,一类是 求出任意一组解 (有时对所求的解有特殊要求，随题意应变即可)。

那么显然是使用tarjan+缩点求解。
正确性是显然的。
考虑边和点的意义，那么一个强连通分量中就代表着取一个该强连通分量中的一个点，则必须取其中的所有点。

因此也就得出了如何判断是否有解的方法：
对于每一个元素i，判断点i与点i+n是否在同一个强连通分量中，如果在，那么就无解，如果都不在，则有解。

然后思考如何得出一个可行解。
根据伍昱 -《由对称性解 2-sat 问题》，可得：
如果要输出 2-SAT 问题的一个可行解，只需要在 tarjan 缩点后所得的 DAG 上自底向上地进行选择和删除。
即按照逆拓扑序求解。

方法一：
可以在DAG上通过拓扑dp求得逆拓扑序，在按照逆拓扑序的顺序处理。

方法二：
建DAG的反图，跑一边拓扑dp，效果和方法一相同。

方法三：这是最简单最常用的一个方法。
根据 tarjan 缩点后，所属连通块编号越小，节点越靠近叶子节点这一性质，优先对所属连通块编号小的节点进行选择。

具体实现选择方法三，即对于一个元素$i$,如果点$i$所在的强连通分量编号较小，则$i$取$1$,否则元素$i$取$0$。

三、解决一些具体问题：（ybtoj例题及洛谷题目）

2-SAT的实际问题解决基本就只有以下几个关键点：
<1>考虑一个变量0/1取值的实际意义
<2>解决题目的特殊要求：例如：要求使n个变量之和最大

T1：洛谷P4782 【模板】2-SAT 问题

一个模板，根据上文的实现思路实现即可。
我出现过的错误：建边的时候建错了一条边，所以说一定要提前固定好点$i$和点$i+n$的实际意义，
出错之后第一之间检查建边是否错误。

Code如下：

#include
using namespace std;
const int maxn=2e6+60;
int n,m;
int dfn[maxn],low[maxn],tot,col[maxn],ans[maxn];
int s[maxn],top,tim;
int head[maxn],ecnt=-1;
struct mint
{
	int nxt,v;	
}e[maxn<<1];
inline void addline(int u,int v)
{
	e[++ecnt].nxt=head[u];
	e[ecnt].v=v;
	head[u]=ecnt;
}
void tarjan(int now)
{
	dfn[now]=low[now]=++tim;
	s[++top]=now;
	for(int i=head[now];~i;i=e[i].nxt)
	{
		int v=e[i].v;
		if(!dfn[v])
		{
			tarjan(v);
			low[now]=min(low[now],low[v]);
		}	
		else if(!col[v]) low[now]=min(low[now],dfn[v]);
	}
	if(dfn[now]==low[now])
	{
		int cur;
		++tot;
		do
		{
			cur=s[top--];
			col[cur]=tot;
		}while(cur!=now);
	}
}
int main()
{
	memset(head,-1,sizeof(head));
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;++i)
	{
		int x,y,a,b;
		scanf("%d%d%d%d",&x,&a,&y,&b);
		if(a==1&&b==1)//b=0 -> a=1 , a=0 ->b=1 
		{
			addline(x+n,y);
			addline(y+n,x);
		}
		if(a==1&&b==0)// a=0 -> b=0 , b=1 -> a=1
		{
			addline(y,x);
			addline(x+n,y+n);	
		}
		if(a==0&&b==1)// a=1 -> b=1 , b=0 -> a=0
		{
			addline(x,y);
			addline(y+n,x+n);		
		}
		if(a==0&&b==0)//a=1 -> b=0 , b=1 -> a=0
		{
			addline(x,y+n);
			addline(y,x+n);
		}
	}
	for(int i=1;i<=n*2;++i) if(!dfn[i]) tarjan(i);
	for(int i=1;i<=n;++i)
	{
		if(col[i]==col[i+n])
		{
			printf("IMPOSSIBLE\n");
			return 0;	
		}
		ans[i]=col[i]<col[i+n];	
	}
	printf("POSSIBLE\n"); 
	for(int i=1;i<=n;++i) printf("%d ",ans[i]);
	return 0;	
}

T2:HDU 3062 Party & YBTOJ |2-SAT| A. 【例题1】聚会

我没有杭电OJ的链接QWQ
题面如下.

显然这是一个2-SAT模板问题，要求判定是否有解即可。
关键在于如何构建模型。
注意这种问题下，虽然表述是n个元素每个元素对应两个人，但是本质上还是n个元素而非2n个元素，即不能将两个人分别当作一个元素，而是要把两个人共同的状态当作元素的意义。
可以发现一对夫妻不能同时出现，那么直接令$1$表示丈夫出席，$0$表示妻子出席。
最终判定有无可行解就是判定一个元素拆成的两点是否在同一个强连通分量中。

Code

#include
using namespace std;
const int maxn=1e6+60;
int n,m;
int head[maxn],ecnt=-1;
int dfn[maxn],low[maxn],col[maxn],tot;
int s[maxn],top,tim;
struct mint
{
	int nxt,v;	
}e[maxn<<1];
inline void addline(int u,int v)
{
	e[++ecnt].nxt=head[u];
	e[ecnt].v=v;
	head[u]=ecnt;	
}
void tarjan(int now)
{
	dfn[now]=low[now]=++tim;
	s[++top]=now;
	for(int i=head[now];~i;i=e[i].nxt)
	{
		int v=e[i].v;
		if(!dfn[v])
		{
			tarjan(v);
			low[now]=min(low[now],low[v]);
		}
		else if(!col[v]) low[now]=min(low[now],dfn[v]);
	}
	if(dfn[now]==low[now])
	{
		int cur;
		++tot;
		do
		{
			cur=s[top--];
			col[cur]=tot;
		}while(cur!=now);
	}
}
int main()
{
	while(scanf("%d",&n)!=EOF)
	{
		scanf("%d",&m);
		memset(dfn,0,sizeof(dfn));
		memset(low,0,sizeof(low));
		memset(col,0,sizeof(col)); 
		ecnt=-1;
		tot=tim=0;
		memset(head,-1,sizeof(head));
		for(int i=1;i<=m;++i)
		{
			int a1,a2,c1,c2;
			scanf("%d%d%d%d",&a1,&a2,&c1,&c2);
			a1=(a1<<1)+c1;
			a2=(a2<<1)+c2;
			addline(a1,a2^1);
			addline(a2,a1^1);
		}
		for(int i=0;i<(n<<1);++i) if(!dfn[i]) tarjan(i);
		int flag=0;
		for(int i=0;i<n;++i)
		{
			if(col[i<<1]==col[(i<<1)^1])
			{
				flag=1;	
				break;	
			}
		}
		if(flag) printf("NO\n");
		else printf("YES\n");	
	}
	return 0;
}

这里再引出一个关键点：关于拆点编号的表示问题

一定要记住，一般情况下，一个元素对应的图上的点一定有且只有两个。
拆点的方法选取一定要满足要求：便于从一个状态迅速找到它的反状态

常见的拆点方法有三种：
<1>将元素 $i$ 拆成 点 $i$ 和点$i+n$。
<2>将元素 $i$ 拆成元素 $i<<1$ 和元素 $(i<<1)+1$(或元素$(i<<1)-1$)
<3>将元素$i$拆成元素$i<<1$ 和 元素 $(i<<1{)}^1$
有时可以直接从$i$找到它的反状态，但是如果无法确定题中给出的输入量是$i$还是$i+n$时，就可以借助一个小函数来找到它的反状态。

int get_id(int x)
{
	return x<n ? x+n : x-n;
}

总之随机应变即可。

T3：UVA11294 Wedding & YBTOJ-B. 【例题2】婚礼

这道题的UVA完整题面是是一个极其混乱的情感大戏
提醒一下：每天UVA都会有一段维护时间，如果你绑定了UVA的账号但是waiting了很久的话，不如换个时间再交

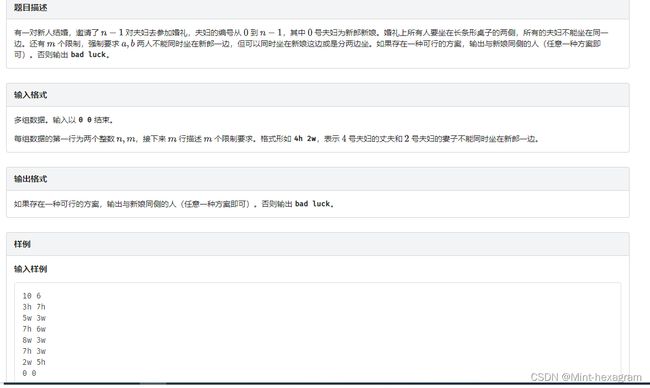
考虑如何建模：
对于一个元素$i$,即一对夫妇，令$0$表示丈夫坐在新郎同侧,$1$表示妻子坐在新郎同侧。
跑一遍2-SAT模板，根据强连通分量的编号序即逆拓扑序这一性质，直接从小到大选即可。

#include
using namespace std;
const int maxn=1e3+30,maxm=1e5+50;
int n,m;
int head[maxn<<2],ecnt=-1;
int dfn[maxn<<2],low[maxn<<2],col[maxn<<2],tot;
int s[maxn<<2],tim,top;
struct mint
{
	int nxt,v;	
}e[maxm<<2];
inline void addline(int u,int v)
{
	e[++ecnt].nxt=head[u];
	e[ecnt].v=v;
	head[u]=ecnt;	
}
void tarjan(int now)
{
	dfn[now]=low[now]=++tim;
	s[++top]=now;
	for(int i=head[now];~i;i=e[i].nxt)
	{
		int v=e[i].v;
		if(!dfn[v])
		{
			tarjan(v);
			low[now]=min(low[now],low[v]);	
		}
		else if(!col[v]) low[now]=min(low[now],dfn[v]);
	}
	if(dfn[now]==low[now])
	{
		int cur;
		++tot;
		do
		{
			cur=s[top--];
			col[cur]=tot;
		}while(cur!=now);
	}
}
int get_id(int x)
{
	if(x<=n) return x+n;
	return x-n;
}
int main()
{
	while(1)
	{
		scanf("%d%d",&n,&m);
		if(n==0&&m==0) return 0;
		memset(head,-1,sizeof(head));
		ecnt=-1;
		memset(dfn,0,sizeof(dfn));
		memset(low,0,sizeof(low));
		memset(col,0,sizeof(col));
		tot=tim=0; 
		for(int i=1;i<=m;++i)
		{
			int x,y,c1=0,c2=0;
			char a,b;
			scanf("%d",&x);
			cin>>a;
			scanf("%d",&y);
			cin>>b;//1~n=w , n+1~n*2=h 
			++x;++y;
			if(a=='h') x+=n;
			if(b=='h') y+=n;
			addline(x,get_id(y));
			addline(y,get_id(x)); 
		}
		addline(1,1+n);
		for(int i=1;i<=2*n;++i) if(!dfn[i]) tarjan(i);
		int flag=0;
		for(int i=1;i<=n;++i)
		{
			if(col[i]==col[i+n])
			{
				flag=1;
				break;
			}
		}
		if(flag)
		{
			printf("bad luck\n");
			continue;
		}
		for(int i=2;i<=n;++i)
		{
			if(col[i]<col[i+n]) printf("%d%c ",i-1,'h');
			else printf("%d%c ",i-1,'w');	
		}
		printf("\n");
	}
	return 0;
}

T4:P5782 [POI2001] 和平委员会 & YBTOJ-D. 和平委员会

说一个有意思的小事情，这道题我先是再ybtoj上过了，然后去csdn搜双倍经验，搜题面第一句话搜不出任何结果，搜后几句就找到了。。。这是什么情况有无大佬解读一下。

继续看题。
一个元素代表一个党派，一个党派必须在议会中有且只有一个席位。
对于元素$i$,考虑$0$表示$2i-1$号代表在议会中，$1$表示$2i$号代表在议会。
跑一遍2-SAT模板然后按照强连通分量编号由小到大选择即可。

#include
using namespace std;
const int maxn=8e3+30,maxm=2e4+50;
int n,m;
int head[maxn<<1],ecnt=-1;
int dfn[maxn<<1],low[maxn<<1],col[maxn<<1],tot;
int s[maxn<<1],top,tim;
struct mint
{
	int nxt,v;	
}e[maxm<<2];
inline void addline(int u,int v)
{
	e[++ecnt].nxt=head[u];
	e[ecnt].v=v;
	head[u]=ecnt;	
}
void tarjan(int now)
{
	dfn[now]=low[now]=++tim;
	s[++top]=now;
	for(int i=head[now];~i;i=e[i].nxt)
	{
		int v=e[i].v;
		if(!dfn[v])
		{
			tarjan(v);
			low[now]=min(low[now],low[v]);
		}
		else if(!col[v]) low[now]=min(low[now],dfn[v]);
	}
	if(dfn[now]==low[now])
	{
		int cur;
		++tot;
		do
		{
			cur=s[top--];
			col[cur]=tot;
		}while(cur!=now);
	}
}
int get_id(int x)
{
	if(x%2==0) return x-1;
	return ++x;	
}
int main()
{
	memset(head,-1,sizeof(head));
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;++i)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		addline(x,get_id(y));
		addline(y,get_id(x));
	}
	for(int i=1;i<=n*2;++i) if(!dfn[i]) tarjan(i);
	int flag=0;
	for(int i=1;i<=n;++i)
	{
		if(col[(i<<1)]==col[(i<<1)-1])
		{
			flag=1;
			break;
		}
	}
	if(flag) 
	{
		printf("NIE\n");
		return 0;	
	}
	for(int i=1;i<=n;++i)
	{
		if(col[(i<<1)]<col[(i<<1)-1]) printf("%d\n",i<<1);
		else printf("%d\n",(i<<1)-1); 
	}
	return 0;
}

我的2-SAT模板跑的还算比较快吧，基本都在最优解前2~3页z左右。

T5:P4171 [JSOI2010] 满汉全席 & YBTOJ-F. 满汉全席

这个题面描述属实是太恶心了，翻译成人话就是：
给出 $n$ 个元素，每个元素有 $0/1$ 两个取值，给出 $m$ 个限制条件，判断有无一个可行解。
水，实在是太水了。
考虑建模，
对于元素 $i$，$0$表示满式做法，$1$表示汉式做法，跑一遍模板，判断是否有解。
水，很水。
但是由于题面过于混乱所以很容易建边建错。。
要注意这一点。
最后，我觉得oi是算法竞赛不是阅读理解竞赛。。。。。
Code

#include
using namespace std;
const int maxn=105,maxm=1005;
int n,m,k;
int head[maxn<<1],ecnt=-1;
int dfn[maxn<<1],low[maxn<<1],col[maxn<<1],tot;
int s[maxn<<1],tim,top;
struct mint
{
	int nxt,v;	
}e[maxm<<1];
inline void addline(int u,int v)
{
	e[++ecnt].nxt=head[u];
	e[ecnt].v=v;
	head[u]=ecnt;	
}
void tarjan(int now)
{
	dfn[now]=low[now]=++tim;
	s[++top]=now;
	for(int i=head[now];~i;i=e[i].nxt)
	{
		int v=e[i].v;
		if(!dfn[v])
		{
			tarjan(v);
			low[now]=min(low[now],low[v]);
		}
		else if(!col[v]) low[now]=min(low[now],dfn[v]);
	}
	if(dfn[now]==low[now])
	{
		int cur;
		++tot;
		do
		{
			cur=s[top--];
			col[cur]=tot;
		}while(cur!=now);
	}
}
int main()
{
	scanf("%d",&k);
	for(int q=1;q<=k;++q)
	{
		scanf("%d%d",&n,&m);	
		memset(head,-1,sizeof(head));
		ecnt=-1;
		memset(dfn,0,sizeof(dfn));
		memset(col,0,sizeof(col));
		memset(low,0,sizeof(low));
		tot=tim=0;
		memset(s,0,sizeof(s));
		top=0;
		int cnt=0;
		for(int i=1;i<=m;++i)
		{
			char a,b;
			int x,y;
			cin>>a;
			scanf("%d",&x);
			cin>>b;
			scanf("%d",&y);
			if(a=='m'&&b=='m')//b=1->a=0 , a=1-->b=0
			{
				addline(y,x+n);
				addline(x,y+n);	
			}
			if(a=='m'&&b=='h')//b=0->a=0 , a=1->b=1
			{
				addline(y+n,x+n);
				addline(x,y);
			}
			if(a=='h'&&b=='m')//b=1->a=1 , a=0->b=0
			{
				addline(x+n,y+n);
				addline(y,x);
			}
			if(a=='h'&&b=='h')//b=0->a=1 , a=0->b=1
			{
				addline(y+n,x);
				addline(x+n,y);
			}
		}
		for(int i=1;i<=n*2;++i) if(!dfn[i]) tarjan(i);
		int flag=0;
		for(int i=1;i<=n;++i)
		{
			if(col[i]==col[i+n])
			{
				flag=1;
				break;
			}
		}
		if(flag) printf("BAD\n");
		else printf("GOOD\n"); 
	}
	return 0;	
}

T6:P3209 [HNOI2010] 平面图判定 & E. 平面图

这是目前提到的6道题中最难也是最好的一道，可惜难点并不在2-SAT上。。。。
题面中提到了平面图，因此肯定要想到平面图的相关定理和相关性质。

平面图就是一张可以画在二维平面上后满足任意两条边不在除顶点意外的位置相交。

首先，题目中给出的$m<=100000$其实是一个假的数据范围，因为根据平面图的性质，
一个平面图一定满足$m<=3\ast n-6$,因此实际上$m$的最大值也才$600$左右。
关于平面图以后我会写博客但是如果想现在了解，请前往OIWIKI的平面图部分。
此处略过。

哈密尔顿路径是一个环。
很容易发现对于一条不在哈密尔顿路径上的边，可以画在哈密尔顿路径内部和外部。
同时，如果两条路径在哈密尔顿路径内部时相交，那么同时在外部时它们也一定相交。

考虑如何建模，将每条不在哈密尔顿路径上的边拆为两个点，分别表示该边画在环内和环外。
对于任意两条非哈密尔顿路径上的边，判断它们同时位于环内时是否相交，
并以此建立限制条件。

图都建完了直接跑一遍模板就可以了。
都做到这一题了判断是否有解应该不是什么问题了。

#include
using namespace std;
const int maxn=250,maxm=1e6+50;
int n,m;
int head[maxm],ecnt=-1;
int dfn[maxm],low[maxm],col[maxm],tot;
int s[maxm],top,tim;
int id[maxm],pla[maxm];
int x[maxm],y[maxm];
bool G[maxn][maxn];
int cnt;
struct mint
{
	int nxt,v;	
}e[maxm<<2];
struct edge
{
	int u,v;
}E[maxm];
inline void addline(int u,int v)
{
	e[++ecnt].nxt=head[u];
	e[ecnt].v=v;
	head[u]=ecnt;	
}
void tarjan(int now)
{
	dfn[now]=low[now]=++tim;
	s[++top]=now;
	for(int i=head[now];~i;i=e[i].nxt)
	{
		int v=e[i].v;
		if(!dfn[v])
		{
			tarjan(v);
			low[now]=min(low[now],low[v]);	
		}
		else if(!col[v]) low[now]=min(low[now],dfn[v]);
	}
	if(dfn[now]==low[now])
	{
		int cur;
		++tot;
		do
		{
			cur=s[top--];
			col[cur]=tot;
		}while(cur!=now);
	}
}
int main()
{
	int t;
	scanf("%d",&t);
	for(int q=1;q<=t;++q)
	{
		memset(head,-1,sizeof(head));
		ecnt=-1;
		memset(dfn,0,sizeof(dfn));
		memset(low,0,sizeof(low));
		memset(col,0,sizeof(col));
		memset(pla,0,sizeof(pla)); 
		memset(G,0,sizeof(G));
		cnt=tim=tot=0;
		scanf("%d%d",&n,&m);
		for(int i=1;i<=m;++i)
		{
			scanf("%d%d",&x[i],&y[i]);	
		}
		for(int i=1;i<=n;++i)
		{
			scanf("%d",&id[i]);
			pla[id[i]]=i;
			G[id[i]][id[i-1]]=G[id[i-1]][id[i]]=1;	
		}
		G[id[1]][id[n]]=G[id[n]][id[1]]=1;
		if(m>3*n-6) 
		{
			printf("NO\n");
			continue;	
		}
		for(int i=1;i<m;++i)
		{
			int a=x[i],b=y[i];
			if(G[a][b]) continue;
			for(int j=i+1;j<=m;++j)
			{
				int c=x[j],d=y[j];
				if(pla[a]>pla[b]) swap(a,b);
				if(pla[c]>pla[d]) swap(c,d);
				if((pla[a]<pla[c] && pla[c]<pla[b] && pla[b]<pla[d]) || (pla[c]<pla[a] && pla[a]<pla[d] && pla[d]<pla[b]))
				{
					addline(i,j+m);
					addline(j,i+m);
					addline(i+m,j);
					addline(j+m,i);
				}
			}
		}
		for(int i=1;i<=m*2;++i) if(!dfn[i]) tarjan(i);
		int flag=0;
		for(int i=1;i<=m;++i)
		{
			if(col[i]==col[i+m]) 
			{
				flag=1;
				break;
			}
		}
		if(flag) printf("NO\n");
		else printf("YES\n");
	}
	return 0;
}	

如何判断两条边在环内相交是一个很重要的小细节：
很容易发现，当一条边和另一条边相交时，一定存在两条边各有一个顶点位于另一条边的两点之间的情况。
手玩一下，多画几种情况就能发现这个结论是恒成立的。

直觉上可能会觉得当一条边跨越n到1时会出现问题，但是事实上任意一条边都可以认为是没有跨过n再到1的。
因此这个结论不会因为是否跨过环的某一位置发生错误

四、后记：

这篇博客存在的意义就是方便大家找到各种双倍经验总结一下2-SAT问题的各种解决思路、错误，以及一些小细节。
实际上这篇博客只是2-SAT的部分题解，很多关键内容例如求出有特殊的集合等都没有被纳入其中。
因此会有下一篇作为补充！耶

一些废话：
所以说其实2-SAT这种代码比较简单模型比较通用的题目似乎不会考的很多啊。。
要不就是一考就出一些看不出是2-SAT的题或者想BJOI完美塔防这样的2-SAT只是次要内容的大模拟。。