最强英文开源模型LLaMA架构探秘,从原理到源码
导读:
LLaMA 65B是由Meta AI(原Facebook AI)发布并宣布开源的真正意义上的千亿级别大语言模型,发布之初(2023年2月24日)曾引起不小的轰动。LLaMA的横空出世,更像是模型大战中一个搅局者。虽然它的效果(performance)和GPT-4仍存在差距,但GPT-4毕竟是闭源的商业模型,LLaMA系列的开源给了世界上其他团队研究和使用千亿大语言模型的机会。
读完本文,你可能觉得LLaMA会开源并不令人惊讶,因为它的架构可以说是站在巨人肩膀上摘苹果——基本上可以说使用其他模型的组件作为“积木”搭了一个新模型出来,并没有太多实质意义上的创新,但这种敢于开源的勇气和做法使得LLaMA足以在大语言模型上的开源发展历程上成为一个标志性的里程碑。
 Introducing LLaMA: A foundational, 65-billion-parameter large language model
Introducing LLaMA: A foundational, 65-billion-parameter large language model
LLaMA开源地址:https://github.com/facebookresearch/llama(llama在llama_v1代码分支上)
正文
llama英文中指大羊驼,是一种分布在南美洲的骆驼科羊驼属动物
LLaMA是一个基于transformer架构的大语言模型,同Google的PaLM一样,针对原始的transformer架构进行了一些“小改进”。整体而言,初版LLaMA的架构和原始transformer有3个大的差异点:
- 前置归一化(Pre-Normalization)[受GPT3启发]:为了提升训练时的稳定性,LLaMA归一化了transformer子层的输入而不是输出,具体使用的正则化方法是
RMSNorm。 - SwiGLU激活函数 [受PaLM启发]:LLaMA使用了和PaLM一样的
SwiGLU激活函数来替代原始的ReLU以提升模型效果。细节上,LLaMA使用dimension为 2 3 4 d \frac{2}{3}4d 324d而不是 4 d 4d 4d。 - 旋转位置编码(Rotary Embedding, Rotary Position Embedding)[受GPTNeo启发]:LLaMA没有使用绝对位置编码(BERT的位置 s i n sin sin、 c o s cos cos编码是一种绝对位置编码),而是使用了相对位置编码
RoPE。
除此之外,一些训练上的细节:
- LLaMA使用
adamW优化器,设置超参数 β 1 = 0.9 \beta_1=0.9 β1=0.9, β 2 = 0.95 \beta_2=0.95 β2=0.95。 - 使用cosine学习率调度,即最终的学习率是最大学习率的10%。
- 权重衰减设置为0.1。
- 梯度剪枝设置为1。
- 2000步热启动(warmup)。
- 不同尺寸的模型使用不同的学习率和batch size。
下面我们来深入了解一下架构上3个差异点的技术细节。
RMSNorm
详细推到过程见原论文:Root Mean Square Layer Normalization
前置归一化(Pre-Normalization)可以使得训练过程更加稳定,这种设计将第一层的归一化设在多头注意力层之前,第二层的归一化移动到全连接层之前,同时将shortcut设置在multi-attention层与FNN层之间。如下如所示:

LLaMA在归一化过程中使用RMSNorm,针对输入向量 a a a,RMSNorm的计算公式如下:
R M S ( a ) = 1 n ∑ i = 1 n a i 2 RMS(a)=\sqrt{\frac{1}{n}\sum_{i=1}^{n}}a_i^2 RMS(a)=n1i=1∑nai2
a i ˉ = a i R M S ( a ) \bar{a_i}=\frac{a_i}{RMS(a)} aiˉ=RMS(a)ai
相较于原始的RMSNorm,LLaMA加入了一个缩放因子 g i g_i gi和一个偏移参数 b i b_i bi(均为可学习参数),最终得到:
a i ˉ = a i R M S ( a ) g i + b i \bar{a_i}=\frac{a_i}{RMS(a)}g_i+b_i aiˉ=RMS(a)aigi+bi
HuggingFace Transformer 库中的LLaMA RMSNorm实现如下:
class LlamaRMSNorm(nn.Module):
def __init__(self, hidden_size, eps=1e-6):
"""
LlamaRMSNorm is equivalent to T5LayerNorm
"""
super().__init__()
self.weight = nn.Parameter(torch.ones(hidden_size))
self.variance_epsilon = eps # eps 防止取倒数之后分母为 0
def forward(self, hidden_states):
input_dtype = hidden_states.dtype
variance = hidden_states.to(torch.float32).pow(2).mean(-1, keepdim=True) hidden_states = hidden_states * torch.rsqrt(variance + self.variance_epsilon) # weight 是末尾乘的可训练参数, 即 g_i
return (self.weight * hidden_states).to(input_dtype)
SwiGLU激活函数
详细推导过程见原论文:GLU Variants Improve Transformer
LLaMA使用的SwiGLU激活函数同时也在PaLM等多个LLM应用,相较于ReLU能在很多评测数据集上提升明显。
LLaMA全连接层使用SwiGLU激活函数的计算公式如下:
F F N S w i G L U ( x , W , V , W 2 ) = S w i G L U ( x , W , V ) W 2 FFN_{SwiGLU}(x,W,V,W_2)=SwiGLU(x,W,V)W_2 FFNSwiGLU(x,W,V,W2)=SwiGLU(x,W,V)W2
S w i G L U ( x , W , V ) = S w i s h β ( x W ) ⊗ x V SwiGLU(x,W,V)=Swish_\beta(xW) \otimes xV SwiGLU(x,W,V)=Swishβ(xW)⊗xV
S w i s h β = x σ ( β x ) Swish_\beta=x\sigma(\beta x) Swishβ=xσ(βx)
其中 σ \sigma σ即sigmoid函数。
S w i s h β Swish_\beta Swishβ函数在参数 β \beta β取值不同时形状不同,如下图:
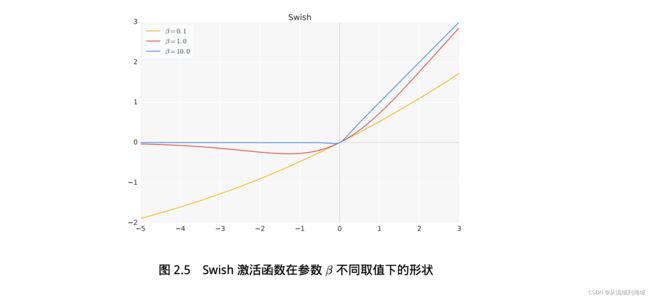
- 当 β → 0 \beta \rightarrow 0 β→0时, S w i s h β → 直线 y = x Swish_\beta \rightarrow 直线 y=x Swishβ→直线y=x
- 当 β → ∞ \beta \rightarrow \infin β→∞时, S w i s h β → R e L U Swish_\beta \rightarrow ReLU Swishβ→ReLU
LLaMA中 β = 1 \beta=1 β=1,维度缩放为 2 3 4 d \frac{2}{3}4d 324d:
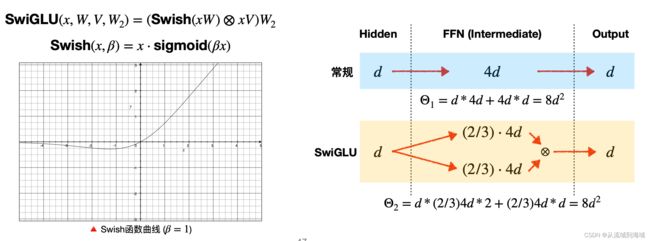
SwishGLU一定程度上引入了Gating机制,原论文实验结果证明了基于Gating的方法普遍优于单纯的激活函数(ReLU
/GELU/Swish)
旋转位置编码 RoPE (Rotary Position Embeddings)
详细推导过程见原论文:ROFORMER: ENHANCED TRANSFORMER WITH ROTARY POSITION EMBEDDING
LLaMA使用RoPE代替原有的绝对位置编码(指BERT的 s i n sin sin、 c o s cos cos位置编码是按固定值计算的,逻辑上表示的位置也是固定的),以取得更好效果。RoPE的数学推导借助了复数的思想,原作者期望通过数学方法基于绝对位置编码的方式实现相对位置编码,进一步讲,存在向量 q q q和 k k k,通过如下运算可以给它们添加绝对位置信息:
q ~ m = f ( q , m ) , k ~ n \tilde{\mathbf{q}}_m=f(\mathbf{q},m),\tilde{\mathbf{k}}_n q~m=f(q,m),k~n
q ~ m \tilde{\mathbf{q}}_m q~m和 k ~ n \tilde{\mathbf{k}}_n k~n具备了 m m m和 n n n的绝对位置信息。
f ( q , m ) ) f(\mathbf{q},m)) f(q,m))经推导如下:
f ( q , m ) ) = R f ( q , m ) e i Θ f ( q , m ) = ∣ ∣ q ∣ ∣ e i ( Θ ( q ) + m θ ) = q e i m θ f(\mathbf{q},m))=R_f(\mathbf{q},m)e^{i\varTheta_f(\mathbf{q},m)}=||\mathbf{q}||e^{i(\varTheta(q)+m\theta)}=\mathbf{q}e^{im\theta} f(q,m))=Rf(q,m)eiΘf(q,m)=∣∣q∣∣ei(Θ(q)+mθ)=qeimθ
(详细推导过程参见源论文)
根据复数乘法的几何意义,上述变换实际上对应向量旋转操作,因而得名“旋转位置编码”,矩阵形式可能能提供不一样的理解:
f ( q , m ) ) = ( c o s m θ − s i n c o s m θ s i n m θ c o s m θ ) ( q 0 q 1 ) f(\mathbf{q},m))=\begin{pmatrix} cos \ m\theta & -sin \ cos \ m\theta \\ sin \ m\theta & cos \ m\theta \end{pmatrix} \begin{pmatrix} \mathbf{q_0} \\ \mathbf{q_1} \end{pmatrix} f(q,m))=(cos mθsin mθ−sin cos mθcos mθ)(q0q1)
根据内积满足线性叠加的性质,任意偶数维上的RoPE,都可以表示为二维情形的拼接,进一步将公式转化为:

上述稀疏矩阵可以使用逐位相乘 ⊗ \otimes ⊗加快计算速度,因而RoPE在HuggingFace Transformer 库中代码实现如下所示:
class LlamaRotaryEmbedding(torch.nn.Module):
def __init__(self, dim, max_position_embeddings=2048, base=10000, device=None):
super().__init__()
inv_freq = 1.0 / (base ** (torch.arange(0, dim, 2).float().to(device) / dim))
self.register_buffer("inv_freq", inv_freq)
# Build here to make `torch.jit.trace` work.
self.max_seq_len_cached = max_position_embeddings
t = torch.arange(self.max_seq_len_cached, device=self.inv_freq.device,
dtype=self.inv_freq.dtype)
freqs = torch.einsum("i,j->ij", t, self.inv_freq)
# Different from paper, but it uses a different permutation
# in order to obtain the same calculation
emb = torch.cat((freqs, freqs), dim=-1)
dtype = torch.get_default_dtype()
self.register_buffer("cos_cached", emb.cos()[None, None, :, :].to(dtype), persistent=False)
self.register_buffer("sin_cached", emb.sin()[None, None, :, :].to(dtype), persistent=False)
def forward(self, x, seq_len=None):
# x: [bs, num_attention_heads, seq_len, head_size]
# This `if` block is unlikely to be run after we build sin/cos in `__init__`. # Keep the logic here just in case.
if seq_len > self.max_seq_len_cached:
self.max_seq_len_cached = seq_len
t = torch.arange(self.max_seq_len_cached, device=x.device, dtype=self.inv_freq.dtype) freqs = torch.einsum("i,j->ij", t, self.inv_freq)
# Different from paper, but it uses a different permutation
# in order to obtain the same calculation
emb = torch.cat((freqs, freqs), dim=-1).to(x.device) self.register_buffer("cos_cached", emb.cos()[None, None, :, :].to(x.dtype),
persistent=False)
self.register_buffer("sin_cached", emb.sin()[None, None, :, :].to(x.dtype),
persistent=False)
return (
self.cos_cached[:, :, :seq_len, ...].to(dtype=x.dtype), self.sin_cached[:, :, :seq_len, ...].to(dtype=x.dtype),
)
def rotate_half(x):
"""Rotates half the hidden dims of the input."""
x1 = x[..., : x.shape[-1] // 2]
x2 = x[..., x.shape[-1] // 2 :]
return torch.cat((-x2, x1), dim=-1)
def apply_rotary_pos_emb(q, k, cos, sin, position_ids):
# The first two dimensions of cos and sin are always 1, so we can `squeeze` them. cos = cos.squeeze(1).squeeze(0) # [seq_len, dim]
sin = sin.squeeze(1).squeeze(0) # [seq_len, dim]
cos = cos[position_ids].unsqueeze(1) # [bs, 1, seq_len, dim]
sin = sin[position_ids].unsqueeze(1) # [bs, 1, seq_len, dim]
q_embed = (q * cos) + (rotate_half(q) * sin)
k_embed = (k * cos) + (rotate_half(k) * sin)
return q_embed, k_embed
不同参数规模的LLaMA模型
基于我们前面讲解的内容,可以实现一个完整的LLaMA Decoder,HuggingFace Transformer库中的实现代码实现如下所示:
class LlamaDecoderLayer(nn.Module):
def __init__(self, config: LlamaConfig):
super().__init__()
self.hidden_size = config.hidden_size
self.self_attn = LlamaAttention(config=config)
self.mlp = LlamaMLP(
hidden_size=self.hidden_size,
intermediate_size=config.intermediate_size,
hidden_act=config.hidden_act,
)
self.input_layernorm = LlamaRMSNorm(config.hidden_size, eps=config.rms_norm_eps)
self.post_attention_layernorm = LlamaRMSNorm(config.hidden_size, eps=config.rms_norm_eps)
def forward(self,
hidden_states: torch.Tensor,
attention_mask: Optional[torch.Tensor] = None,
position_ids: Optional[torch.LongTensor] = None,
past_key_value: Optional[Tuple[torch.Tensor]] = None,
output_attentions: Optional[bool] = False,
use_cache: Optional[bool] = False,
) -> Tuple[torch.FloatTensor, Optional[Tuple[torch.FloatTensor, torch.FloatTensor]]]:
residual = hidden_states
hidden_states = self.input_layernorm(hidden_states)
# Self Attention
hidden_states, self_attn_weights, present_key_value = self.self_attn(
hidden_states=hidden_states,
attention_mask=attention_mask,
position_ids=position_ids,
past_key_value=past_key_value,
output_attentions=output_attentions,
use_cache=use_cache,
)
hidden_states = residual + hidden_states
# Fully Connected
residual = hidden_states
hidden_states = self.post_attention_layernorm(hidden_states)
hidden_states = self.mlp(hidden_states)
hidden_states = residual + hidden_states
outputs = (hidden_states,)
if output_attentions:
outputs += (self_attn_weights,)
if use_cache:
outputs += (present_key_value,)
return outputs
再按架构即可可以实现整个LLaMA模型。
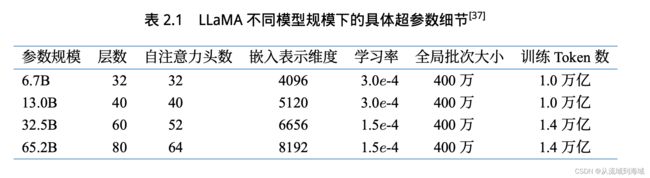
Meta一共发布了4种尺寸的LLaMA,不同尺寸模型的的细节区别如下:
预训练 Pre-Training
预训练数据集对模型效果有深刻影响,LLaMA使用的混合数据集配比以及大小如下:

预训练数据集经token化之后总计1.4T个token,对于大多数预训练token仅使用一次,但Wikipedia和Books数据集训练了2轮。
指令精调 Instruction Finetuning
在LLaMA论文里,原作者尝试对LLaMA做了一个简单的指令精调,结果在MMLU数据集上有5.4%提升:

指令精调的细节参见:Scaling Instruction-Finetuned Language Models,作者为了针对模型效果作对比采用了同样的流程。
结语
LLaMA的架构探秘止步于此。
随着大模型的参数逐步增大,模型的整体架构已不足以对最终效果决定性影响,反而数据集和架构上的一些小细节决定了模型的最终效果。LLaMA虽然没有特别亮眼的创新,但是它的一些实验性的结论,也对后面的模型设计和训练提供了良好的借鉴意义。作为第一个开源的由业界顶尖公司发布的大模型,LLaMA实际上起到了大模型开源进程的奠基作用。
希望未来能看到越来越多的大模型开源,也希望自然语言处理能真正为人类的生产力带来更多可实地落地的突破。
参考文献
- LLaMA: Open and Efficient Foundation Language Models
- Introducing LLaMA: A foundational, 65-billion-parameter large language model
- 大规模语言模型:从原理到实践(复旦NLP教材)
- 大规模预训练语言模型方法与实践 (崔一鸣 北京·BAAI 2023年8月26日)
- Root Mean Square Layer Normalization
- GLU Variants Improve Transformer
- ROFORMER: ENHANCED TRANSFORMER WITH ROTARY POSITION EMBEDDING
- Scaling Instruction-Finetuned Language Models