算法刷题-链表

算法刷题-链表

203. 移除链表元素

给你一个链表的头节点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的节点，并返回 新的头节点 。

示例 1：

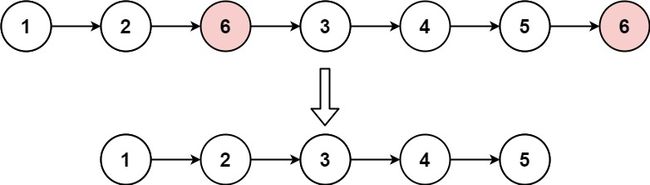
输入：head = [1,2,6,3,4,5,6], val = 6
输出：[1,2,3,4,5]

思路

建立一个虚拟头节点，指向链表的头节点，然后再遍历链表删除值为val的节点，这样比较好方便删除头节点

代码

    ListNode* removeElements(ListNode* head, int val) {
        ListNode* head2 =new ListNode(0);
        head2->next=head;
        ListNode* cur=head2;
        while(cur->next!=NULL){
            if(cur->next->val==val){
                ListNode* tmp=cur->next;
                cur->next=tmp->next;
                delete tmp;
            }else{
                cur=cur->next;
            }
        }
        head=head2->next;
        delete head2;
        return head;
    }

707. 设计链表

你可以选择使用单链表或者双链表，设计并实现自己的链表。

单链表中的节点应该具备两个属性：val 和 next 。val 是当前节点的值，next 是指向下一个节点的指针/引用。

如果是双向链表，则还需要属性 prev 以指示链表中的上一个节点。假设链表中的所有节点下标从 0 开始。

实现 MyLinkedList 类：

• MyLinkedList() 初始化 MyLinkedList 对象。
• int get(int index) 获取链表中下标为 index 的节点的值。如果下标无效，则返回 -1 。
• void addAtHead(int val) 将一个值为 val 的节点插入到链表中第一个元素之前。在插入完成后，新节点会成为链表的第一个节点。
• void addAtTail(int val) 将一个值为 val 的节点追加到链表中作为链表的最后一个元素。
• void addAtIndex(int index, int val) 将一个值为 val 的节点插入到链表中下标为 index 的节点之前。如果 index 等于链表的长度，那么该节点会被追加到链表的末尾。如果 index 比长度更大，该节点将 不会插入 到链表中。
• void deleteAtIndex(int index) 如果下标有效，则删除链表中下标为 index 的节点。

思路

注意野指针

代码

class MyLinkedList {
public:
    struct node {
        int val;
        node *next;

        node(int x) : val(x), next(nullptr) {}
    };

    MyLinkedList() {
        sz = 0;
        head = new node(0);
    }

    int get(int index) {
        node *cur = head->next;
        if (index < 0 || index >= sz) return -1;
        while (index--) cur = cur->next;
        return cur->val;
    }

    void addAtHead(int val) {
        addAtIndex(0, val);
    }

    void addAtTail(int val) {
        addAtIndex(sz, val);
    }

    void addAtIndex(int index, int val) {
        if (index > sz)return;
        if (index < 0) index = 0;
        node *cur = head;
        while (index-- > 0) cur = cur->next;
        node *tmp = new node(val);
        tmp->next = cur->next;
        cur->next = tmp;
        sz++;
    }

    void deleteAtIndex(int index) {
        if (index < 0 || index >= sz)return;
        node *cur = head;
        while (index--) cur = cur->next;
        node *tmp = cur->next;
        cur->next = tmp->next;
        delete tmp;
        tmp = nullptr;//防止野指针
        sz--;
    }

private:
    int sz;
    node *head;
};

206. 反转链表

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

思路

让每个节点指向前面的节点即可

代码

    ListNode* reverseList(ListNode* head) {
        ListNode* right;
        ListNode* cur=head;
        ListNode* pre=nullptr;
        while(cur){
            right=cur->next;
            cur->next=pre;
            pre=cur;
            cur=right;
        }
        return  pre;
    }

24. 两两交换链表中的节点

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

示例 1：

输入：head = [1,2,3,4]
输出：[2,1,4,3]

思路

参考代码随想录中的反转步骤，还是用到虚拟头节点：

代码

    ListNode *swapPairs(ListNode *head) {
        ListNode *dummyHead = new ListNode(0);
        dummyHead->next = head;
        ListNode *cur = dummyHead;
        while (cur->next != nullptr && cur->next->next != nullptr) {
            ListNode *node1 = cur->next;
            ListNode *node2 = node1->next;
            ListNode *node3 = node2->next;
            cur->next = node2;
            node2->next = node1;
            node1->next = node3;
            cur = node1;
        }
        return dummyHead->next;
    }

19. 删除链表的倒数第 N 个结点

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例 1：

输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

思路

双指针，让快指针先走n+1步，然后慢指针从头节点开始和快指针一起走，

当快指针走到最后的时候，此时慢指针的下一个节点就是倒数第N个节点，删除即可

代码

    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummy =new ListNode(0);
        dummy->next=head;
        ListNode* fast= dummy;
        ListNode* slow =dummy;
        n++;
        while(n--) fast=fast->next;
        while(fast!=nullptr) fast=fast->next,slow=slow->next;
        ListNode* tmp=slow->next;
        slow->next=tmp->next;
        delete tmp;
        return dummy->next;
    }

面试题 02.07. 链表相交

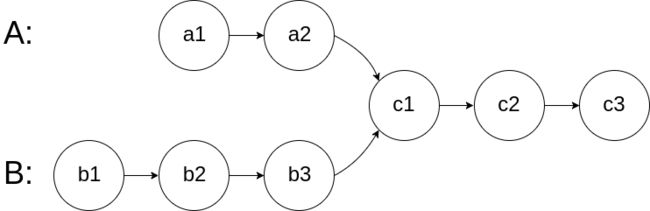
给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。

图示两个链表在节点 c1 开始相交**：**

题目数据 保证 整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

思路

因为相交肯定是从最后一个开始香蕉

先计算两个链表的长度，然后让链表长度长的先把多出来的部分走完，再一起往前走，知道相同为止

代码

    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        int n=0,m=0;
        ListNode *dummy=headA;
        while(dummy!=nullptr) n++,dummy=dummy->next;
        dummy=headB;
        while(dummy!=nullptr) m++,dummy=dummy->next;
        ListNode* curA=headA;
        ListNode* curB=headB;
        if(m>n) swap(curA,curB),swap(n,m);
        while(n>m) curA=curA->next,n--;
        while(curA!=nullptr){
            if(curA==curB) return curA;
            curA=curA->next,curB=curB->next;
        }
        return nullptr;
    }

142. 环形链表 II

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

思路

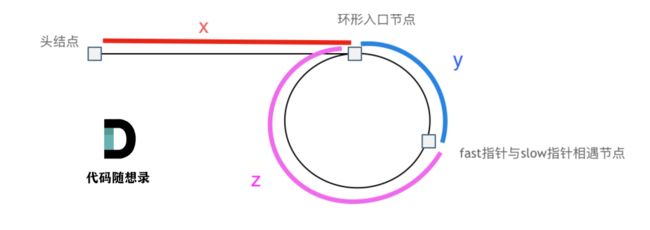
代码随想录：

相遇时：

slow指针走了$x+y$

fast指针走了$x+y+n(y+z)$

因此：$2(x+y)=x+y+n(y+z)$

化简得：$x=n(y+z)-y$

整理得:$x=(n-1)(y-z)+z$

当$n=1$的时候，$x=z$

也就是说：从相遇点和头节点开始同时走，他们第一次相遇的时候就是环形的入口。

代码

    ListNode *detectCycle(ListNode *head) {
        ListNode *fast=head;
        ListNode *slow=head;
        while(fast!=nullptr &&fast->next!=nullptr){
            slow=slow->next;
            fast=fast->next->next;
            if(slow==fast){
                ListNode *a=head;
                ListNode *b=fast;
                while(a!=b) a=a->next,b=b->next;
                return a;
            }
        }
        return nullptr;
    }