算法笔记:双指针法(数组移除元素)
1 数组移除元素
给定一个数组nums和一个值val,在不使用额外数组空间的情况下移除数组中所有数值等于val的元素,并返回数组的新长度,数组中超出新长度后面的元素无需考虑。
注:数组的元素在内存地址中是连续的,无法单独删除数组中的某个元素,只能对数组元素作覆盖。
2 解法
2.1 暴力解法
2.1.1 解题思路
嵌套两层 for 循环,外层遍历数组元素,找到要移除的元素后,内层循环更新数组。
时间复杂度:O(n2)
空间复杂度:O(1)
2.1.2 图解移除元素过程
2.1.3 Java 代码实现
public int removeElement(int[] nums, int val) {
// 数组长度
int length = nums.length;
// 外层遍历数组元素,查找要移除的元素
for (int i = 0; i < length; i++) {
if (nums[i] == val) {
// 找到要移除的元素,就将后面的元素整体向前移动一位
for (int j = i + 1; j < length; j++) {
nums[j - 1] = nums[j];
}
// 下标 i 后的数组元素均向前移动了一位,故 i 也向前移动一位
i--;
// 数组长度-1
length--;
}
}
return length;
}
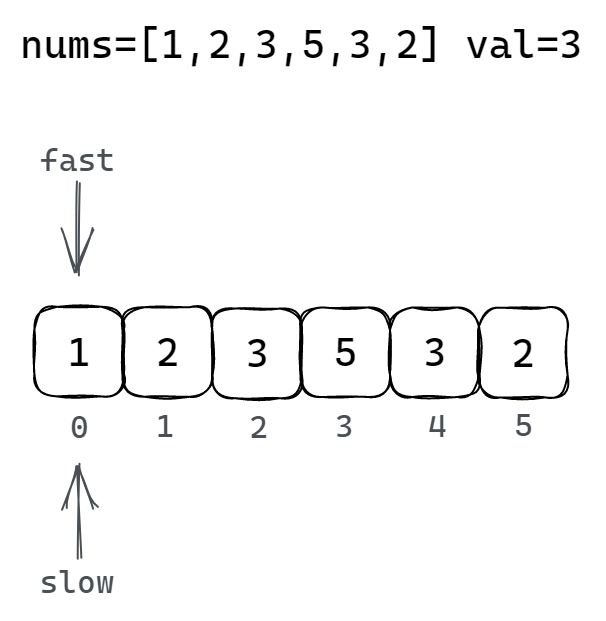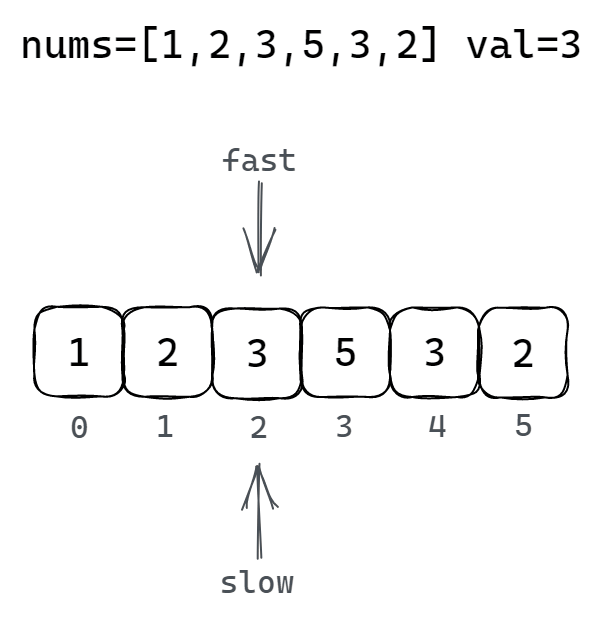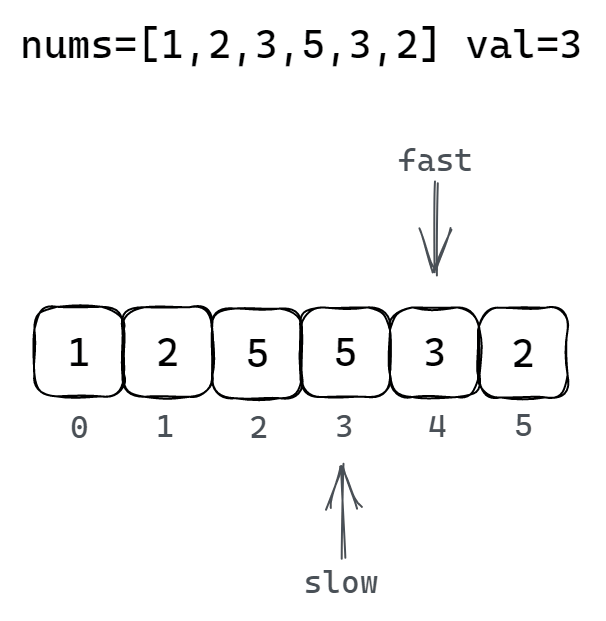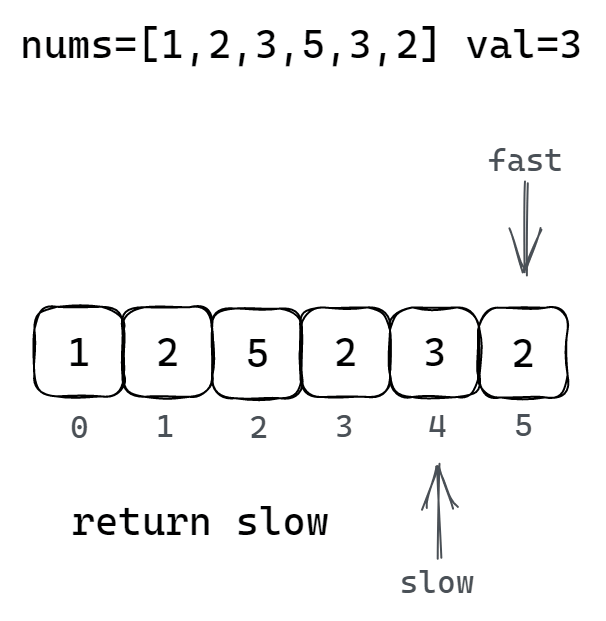
2.2 双指针法
2.2.1 解题思路
通过一个快指针和一个慢指针在一个 for 循环下完成移除元素的查找和数组元素的移动更新两个操作:
快指针:循环遍历数组所有元素,然后将快指针指向的非移除元素的元素值覆盖慢指针所指向的元素
慢指针:指向要覆盖的元素位置(只有发生了被覆盖的操作慢指针才会继续向后移动)
2.2.2 图解移除元素过程
2.2.3 Java 代码实现
public static int removeElement02(int[] nums, int val) {
int slowIndex = 0;
// 快指针遍历所有元素
for (int fastIndex = 0; fastIndex < nums.length; fastIndex++) {
// 非要移除的元素,则将快指针的元素值覆盖慢指针的元素值
if (nums[fastIndex] != val) {
nums[slowIndex] = nums[fastIndex];
// 覆盖操作后,慢指针继续向后移动
slowIndex++;
}
}
// 最后得到数组的新长度即为慢指针的下标值
return slowIndex;
}
2.2.4 优化双指针
2.2.4.1 优化思路
题目描述允许元素顺序改变,所以可以使用相向的双指针遍历,只覆盖要移除的元素位置,避免了需要保留的元素的重复赋值
2.2.4.2 图解移除元素过程
2.2.4.3 代码实现
public static int removeElement03(int[] nums, int val) {
// 左指针:指向第一个元素
int left = 0;
// 右指针:指向最后一个元素
int right = nums.length - 1;
// 当 left == right + 1 时,左右指针遍历完数组中所有的元素
while (left <= right) {
// 如果左指针指向的元素是要移除的元素,则将右指针的元素覆盖左指针,然后右指针向左移动,否则左指针继续向右移动
if (nums[left] == val) {
nums[left] = nums[right];
right--;
} else {
left++;
}
}
// 最后得到数组的新长度即为右指针的下标值
return left;
}
3 相关题目(题目来源:Leetcode)
3.1 删除排序数组中的重复项
3.1.1 题目描述
给你一个 升序排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。
由于在某些语言中不能改变数组的长度,所以必须将结果放在数组 nums 的第一部分。更规范地说,如果在删除重复项之后有 k 个元素,那么 nums 的前 k 个元素应该保存最终结果。
将最终结果插入 nums 的前 k 个位置后返回 k 。
不要使用额外的空间,你必须在 原地 并在使用 O(1) 额外空间的条件下完成。
判题标准:
系统会用下面的代码来测试你的题解:
int[] nums = [...]; // 输入数组
int[] expectedNums = [...]; // 长度正确的期望答案
int k = removeDuplicates(nums); // 调用
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums[i] == expectedNums[i];
}
如果所有断言都通过,那么您的题解将被 通过。
示例 1
输入:nums = [1,1,2]
输出:2, nums = [1,2,_]
解释:函数应该返回新的长度 2 ,并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
示例 2
输入:nums = [0,0,1,1,1,2,2,3,3,4]
输出:5, nums = [0,1,2,3,4]
解释:函数应该返回新的长度 5 , 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
题目来源
- 26. 删除有序数组中的重复项 - 力扣(Leetcode)
3.1.2 解题思路
双指针法
3.1.3 Java 代码实现
public int removeDuplicates(int[] nums) {
int slowIndex = 0;
// 快指针遍历所有元素
for (int fastIndex = 0; fastIndex < nums.length; fastIndex++) {
// 快指针找到不同元素后,将慢指针向后移动,并将新的元素赋值给慢指针
if (nums[fastIndex] != nums[slowIndex]) {
slowIndex++;
nums[slowIndex] = nums[fastIndex];
}
}
// 此时慢指针指向的是新数组的最后一个元素,返回新数组长度则加1
return slowIndex + 1;
}
3.2 移动零
3.2.1 题目描述
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2
输入: nums = [0]
输出: [0]
题目来源
- 283. 移动零 - 力扣(Leetcode)
3.2.2 解题思路
双指针,q指针遍历所有元素找到非0值则与p指针交换元素值,然后p指针指向下一元素值
3.2.3 Java 代码实现
public void moveZeroes(int[] nums) {
int p = 0;
for (int q = 0; q < nums.length; q++) {
// q指针指向的当前元素非0,则与p指针交换元素值,然后p指针指向下一元素值
if (nums[q] != 0) {
int tmp = nums[p];
nums[p] = nums[q];
nums[q] = tmp;
p++;
}
}
}
3.3 比较含退格的字符串
3.3.1 题目描述
给定 s 和 t 两个字符串,当它们分别被输入到空白的文本编辑器后,如果两者相等,返回 true 。# 代表退格字符。
**注意:**如果对空文本输入退格字符,文本继续为空。
示例 1
输入:s = "ab#c", t = "ad#c"
输出:true
解释:s 和 t 都会变成 "ac"。
示例 2
输入:s = "ab##", t = "c#d#"
输出:true
解释:s 和 t 都会变成 ""。
示例 3
输入:s = "a#c", t = "b"
输出:false
解释:s 会变成 "c",但 t 仍然是 "b"。
题目来源
- 844. 比较含退格的字符串 - 力扣(Leetcode)
3.3.2 解题思路
3.3.2.1 重构字符串
重构字符串,将字符串中的退格符以及需要删除的字符去掉,得到的两个字符串进行比较
使用栈处理:如果是退格符则将栈顶字符弹出;非退格符则压入栈中
3.3.2.2 双指针
双指针,分别指向两个字符串的末端,往前遍历,记录需要退格的数量
直至两个字符串都能确定一个字符时,比较两个字符,不相同则返回false,相同则继续遍历直至结束
3.3.3 Java 代码实现
3.3.3.1 重构字符串
public boolean backspaceCompare(String s, String t) {
return build(s).equals(build(t));
}
/**
* 重构字符串
*/
private String build(String str) {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < str.length(); i++) {
if (str.charAt(i) == '#') {
// 说明栈顶有值,将该字符从栈顶弹出
if (sb.length() != 0) {
sb.deleteCharAt(sb.length() - 1);
}
} else {
// 非退格符,将该字符压入栈中
sb.append(str.charAt(i));
}
}
return sb.toString();
}
3.3.3.2 双指针
public boolean backspaceCompare(String s, String t) {
// 定义两个指针,分别指向两个字符串的末端
int i = s.length() - 1;
int j = t.length() - 1;
// 定义两个记录退格数的变量
int skipS = 0;
int skipT = 0;
while (i >= 0 || j >= 0) {
// 确定s字符串的字符
while (i >= 0) {
if (s.charAt(i) == '#') {
skipS++;
i--;
} else if (skipS != 0) {
skipS--;
i--;
} else {
break;
}
}
// 确定t字符串的字符
while (j >= 0) {
if (t.charAt(j) == '#') {
skipT++;
j--;
} else if (skipT != 0) {
skipT--;
j--;
} else {
break;
}
}
if (i < 0 || j < 0) {
// 当 i < 0,j > 0 或者 i > 0,j < 0 时,两个字符串必不相同,返回 false
// 当 i < 0,j < 0 时,两个字符串都是空串,返回 true
return i < 0 && j < 0;
}
// 当 i >= 0,j >= 0 时,才会走到这里去进行字符的比较
// 比较两个字符
if (s.charAt(i) != t.charAt(j)) {
return false;
}
i--;
j--;
}
return true;
}
3.4 有序数组的平方
3.4.1 题目描述
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]
示例 2
输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]
题目来源
- 977. 有序数组的平方 - 力扣(Leetcode)
3.4.2 解题思路
3.4.2.1 暴力解法
数组每个元素平方,得到新数组后进行排序,时间复杂度为O(nlog n)
3.4.2.2 双指针法
双指针法,题干说明数组是非递减顺序排序,所以数组中存在以下三种情况:
(1)全是非负数,则平方后的数组单调递增;
(2)全是负数,则平方后的数组单调递减;
(3)正负数都有,则平方后的数组先单调递减再单调递增。
无论上述哪种情况,最大值都是在数组两端,往中间逐渐递减。
分别在两端定义两个指针,往中间遍历,每次循环找到当前最大值存入新数组,时间复杂度为O(n)
3.4.3 Java 代码实现
3.4.3.1 暴力解法
public int[] sortedSquares(int[] nums) {
// 先平方
for (int i = 0; i < nums.length; i++) {
nums[i] = nums[i] * nums[i];
}
// 后排序
Arrays.sort(nums);
return nums;
}
3.4.3.2 双指针法
public int[] sortedSquares(int[] nums) {
// p指针指向最左侧
int p = 0;
// q指针指向最右侧
int q = nums.length - 1;
// 定义一个和nums一样长度的新数组
int i = nums.length;
int[] ans = new int[i];
// 当 p > q 时,所有元素均已遍历,循环终止
while (p <= q) {
// 两端值的平方,较大者存入新数组,对应指针向中间移动
if (nums[p] * nums[p] > nums[q] * nums[q]) {
ans[i - 1] = nums[p] * nums[p];
p++;
} else {
ans[i - 1] = nums[q] * nums[q];
q--;
}
// 新数组下标左移一位
i--;
}
return ans;
}