Leetcode刷题113. 路径总和 II

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

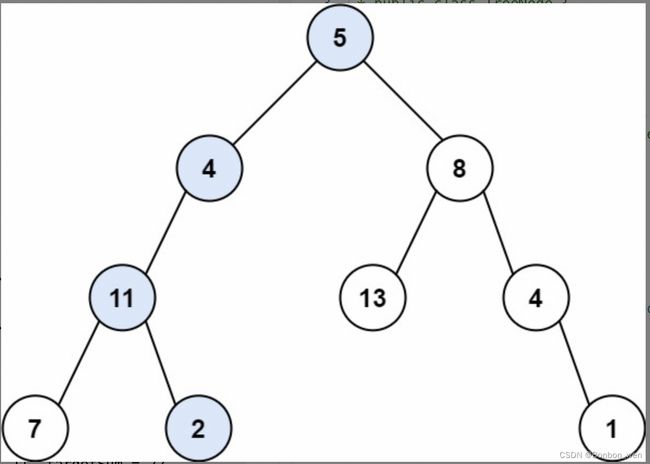
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：

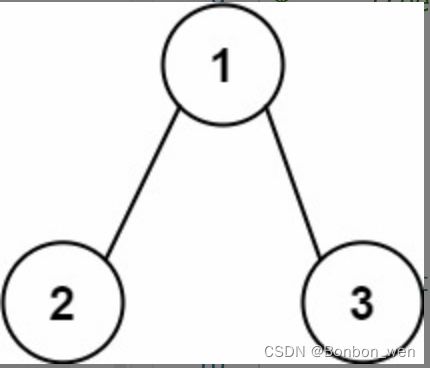
输入：root = [1,2,3], targetSum = 5
输出：[]

示例 3：

输入：root = [1,2], targetSum = 0
输出：[]

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/path-sum-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

class Solution {
    public List> pathSum(TreeNode root, int targetSum) {
//		return pathSumI(root, targetSum);
//		return pathSumII(root, targetSum);
//		return pathSumIII(root, targetSum);
		return pathSumIIII(root, targetSum);
	}

	//方法四：与102题类似，使用栈，利用后序遍历
	private List> pathSumIIII(TreeNode root, int targetSum) {
		List> result = new ArrayList<>();
		if (root == null) {
			return result;
		}
		Stack stack = new Stack<>();
		List tempList = new ArrayList<>();
		TreeNode prev = null;
		int curSum = 0;
		while (!stack.isEmpty() || root != null) {
			while (root != null) {
				stack.push(root);
				tempList.add(root.val);
				curSum += root.val;
				root = root.left;
			}
			TreeNode node = stack.peek();
			if (node.left == null && node.right == null && curSum == targetSum) {
				result.add(new ArrayList<>(tempList));
			}
			if (node.right != null && node.right != prev) {
				root = node.right;
			} else {
				TreeNode pop = stack.pop();
				curSum -= pop.val;
				tempList.remove(tempList.size() - 1);
				prev = node;
			}
		}
		return result;
	}

	//方法三：BFS遍历，时间复杂度O(N^2)，空间复杂度O(N)
	private List> pathSumIII(TreeNode root, int targetSum) {
		List> result = new ArrayList<>();
		if (root == null) {
			return result;
		}
		Queue queue = new LinkedList<>();
		queue.offer(root);
		List list = new ArrayList<>();
		list.add(root.val);
		Queue> queueList = new LinkedList<>();
		queueList.offer(list);
		while (!queue.isEmpty()) {
			int size = queue.size();
			while (size-- > 0) {
				TreeNode node = queue.poll();
				List tempList = queueList.poll();
				if (node.left == null && node.right == null && node.val == targetSum) {
					result.add(tempList);
				}
				if (node.left != null) {
					tempList.add(node.left.val);
					queueList.offer(new ArrayList<>(tempList));
					node.left.val += node.val;
					queue.offer(node.left);
					//这里为了防止分支污染，需要将刚刚添加的元素剔除
					tempList.remove(tempList.size() - 1);
				}
				if (node.right != null) {
					tempList.add(node.right.val);
					queueList.offer(new ArrayList<>(tempList));
					node.right.val += node.val;
					queue.offer(node.right);
					tempList.remove(tempList.size() - 1);
				}
			}
		}
		return result;
	}

	//方法二：方法一在递归时为了防止分支污染每次都要创建新的List，其实还可以把使用过的值在返回的时候把它给remove掉
	//时间复杂度O(N^2)，空间复杂度O(N)
	private List> pathSumII(TreeNode root, int targetSum) {
		List> result = new ArrayList<>();
		if (root == null) {
			return result;
		}
		recursive(root, targetSum, result, new ArrayList<>());
		return result;
	}

	private void recursive(TreeNode root, int sum, List> result, List list) {
		if (root == null) {
			return;
		}
		//这里使用前序遍历，是因为前序位置的代码在刚刚进入一个二叉树节点的时候执行，这里就是刚进入节点时进行判断
		list.add(root.val);
		if (root.left == null && root.right == null && sum == root.val) {
			result.add(new ArrayList<>(list));
		}
		recursive(root.left, sum - root.val, result, list);
		recursive(root.right, sum - root.val, result, list);
		//递归结束后，要把之前加入的元素删除，不要影响到其他分支的list
		list.remove(list.size() - 1);
	}

	//方法一：递归，时间复杂度O(N^2)，空间复杂度O(N)
	private List> pathSumI(TreeNode root, int targetSum) {
		List> result = new ArrayList<>();
		if (root == null) {
			return result;
		}
		dfs(root, targetSum, result, new ArrayList<>());
		return result;
	}

	private void dfs(TreeNode root, int sum, List> result, List list) {
		if (root == null) {
			return;
		}
		//这里为了防止递归的时候分支污染，我们要在每个路径中都要新建一个subList
		List subList = new ArrayList<>(list);
		subList.add(root.val);
		if (root.left == null && root.right == null && root.val == sum) {
			result.add(subList);
		}
		dfs(root.left, sum - root.val, result, subList);
		dfs(root.right, sum - root.val, result, subList);
	}
}