CAD模型旋转和AX=B的数值方法——《数值计算方法》
《数值计算方法》系列总目录
第一章 误差序列实验
第二章 非线性方程f(x)=0求根的数值方法
第三章 CAD模型旋转和AX=B的数值方法
第四章 插值与多项式逼近的数值计算方法
第五章 曲线拟合的数值方法
第六章 数值微分计算方法
第七章 数值积分计算方法
第八章 数值优化方法
第三章
- 一、算法原理
-
-
- 1、CAD模型旋转原理
- 2、三角分解法原理
- 3、雅可比迭代法和高斯-赛德尔迭代法
-
- 二、实验内容及核心算法代码
-
-
- 1、CAD模型旋转原理实现
- 2、三角分解法原理
- 3、雅可比迭代法和高斯-赛德尔迭代法实现
-
- 三、实验数据结果分析
-
-
- 1、CAD模型旋转
- 三角分解法
- 雅可比迭代法和高斯-赛德尔迭代法
-
- 四、结论
一、算法原理
1、CAD模型旋转原理
设 U = [ x y z ] ’ U=[x y z]’ U=[xyz]’是一个 3 × 1 3×1 3×1矩阵,可将 U U U矩阵视为一个笛卡尔坐标系中的三维列向量,设A是一个 3 × 3 3×3 3×3矩阵,那么定义乘积矩阵 V = A U V=AU V=AU为另外一个 3 × 1 3×1 3×1矩阵,为 U U U矩阵表示的空间向量的一个线性变换,其中得到的矩阵 U U U为变换后所表示的三维列向量。那么,不难看出,只要给定一个三维列向量 U U U,任意一种变换都有唯一一个矩阵A与之一一对应。因此,在计算机图形学领域中,可以通过仔细设计矩阵A来进行对坐标的任意变换。下面考虑三个特殊的三维矩阵:
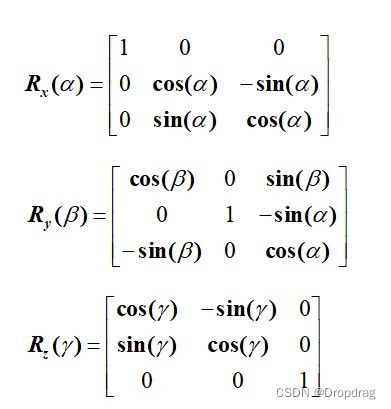
根据矩阵的运算性质,以第一个矩阵的线性变换为例,设 U = [ x y z ] ’ U=[x y z]’ U=[xyz]’是一个 3 × 1 3×1 3×1矩阵,设 V V V矩阵为进行线性变换后的矩阵,则可知矩阵V= R x ( α ) {R_x}(\alpha ) Rx(α)×U的结果如下:
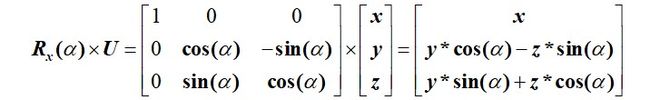
则可知,变换后的U向量以角度 α α α绕 x x x轴旋转。以此类推,矩阵 R x ( α ) {R_x}(\alpha ) Rx(α)、 R y ( β ) {R_y}(\beta ) Ry(β)、 R z ( γ ) {R_z}(\gamma ) Rz(γ)分别用来对向量U进行以角度 α 、 β α、β α、β和 γ γ γ绕 x x x轴、 y y y轴和 z z z轴旋转。他们的反向为 R x ( − α ) {R_x}(-\alpha ) Rx(−α)、 R y ( − β ) {R_y}(-\beta ) Ry(−β)、 R z ( − γ ) {R_z}(-\gamma ) Rz(−γ),在x轴、y轴和z轴上旋转的角度分别是 − α 、 − β -α、-β −α、−β和 − γ -γ −γ。因此,定义一个三维立方体,对其各个顶点的列向量用以上三个矩阵进行线性变换,便是CAD模型旋转的基本原理。换言之,就是用以上三个三维矩阵与三维空间中一个列向量的矩阵相乘,得到的新的三维矩阵即是进行旋转后的三位列向量。
2、三角分解法原理
三角分解法的基本思想为,一个方阵可分解成两个矩阵的乘积,当给定一些约束后,这些分解将是唯一的。对矩阵进行三角分解实际上只是将矩阵分解成上三角矩阵和下三角矩阵的乘积,这样对任意方程组的求解问题就转化为三角形方程组的求解问题,方便利用回代算法计算。
对LU分解法的定义为,对于一个矩阵A,若存在n阶下三角方阵L和上三角方阵U,使得A=LU,则称方阵A有三角分解或LU分解。其中,下三角矩阵的特点为其主对角线上的元素全为1。其分解后的形式如下
对于一个4×4矩阵,其LU分解后的形式为

不难证明,如果矩阵A为奇异矩阵,则其不存在LU分解。对A进行分解以后,线性方程组便可以写成
A X = B ⇒ L U X = B AX = B \Rightarrow LUX = B AX=B⇒LUX=B
则线性方程组的求解可以化简为求解两个上三角矩阵构成的线性方程组的求解问题,大大简化了计算量。其两个上三角矩阵构成的线性方程组如下:
l e t U X = Y ⇒ L Y = B a n d U X = Y let{\rm{ UX = Y}} \Rightarrow {\rm{LY = B and UX = Y}} letUX=Y⇒LY=BandUX=Y
LU分解的基本原理为,对于任意一个矩阵A,由于其是可逆矩阵,则其可以看成是多个初等矩阵的乘积。其中,对于某个可逆矩阵
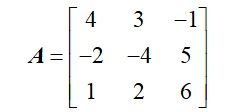
其可以写成为
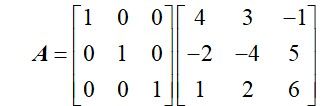
于是,对A进行行初等变换,即在A矩阵左边乘以行初等变换的矩阵,便将右边矩阵转化为上三角矩阵,类似于高斯消元过程。
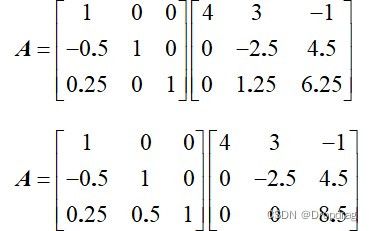
其中,L下三角矩阵保留了进行行初等变换的系数,利用高斯消元的步骤可以求出L矩阵的具体数值。
LU分解法的大致过程为,对于第1行开始,将高斯消元法的系数保留在下三角矩阵中的第1列中,并对以下的每一行(除去第一列)施以高斯消元的步骤
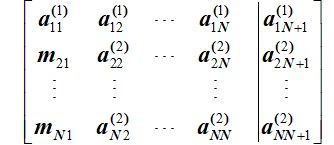
于是,以下的第k行进行同样的变换,最终便可得到L、U矩阵。
3、雅可比迭代法和高斯-赛德尔迭代法
迭代法求解线性方程组的解的基本思想是,给定一个初始的近似解,利用线性方程组进行迭代,每次迭代产生一个比原来解更接近精确解的向量,直到最终解向量收敛于精确解向量,即小于给定精度范围。但是,有时候迭代法会产生一个发散的序列,则此时迭代法便是失效的。雅可比迭代法和高斯-赛德尔迭代法的基本步骤如下。
对于一个给定的线性方程组
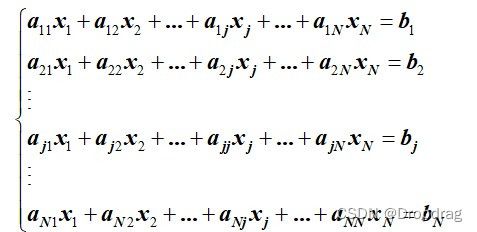
其雅可比迭代法每一次迭代的迭代式为
J a c o b i : x j ( k + 1 ) = b j − a j 1 x 1 ( k ) − . . . − a j j − 1 x j − 1 ( k ) − a j j + 1 x j + 1 ( k ) − . . . − a j N x N ( k ) a j j Jacobi:x_j^{(k + 1)} = \frac{{{b_j} - {a_{j1}}x_1^{(k)} - ... - {a_{jj - 1}}x_{j - 1}^{(k)} - {a_{jj + 1}}x_{j + 1}^{(k)} - ... - {a_{jN}}x_N^{(k)}}}{{{a_{jj}}}} Jacobi:xj(k+1)=ajjbj−aj1x1(k)−...−ajj−1xj−1(k)−ajj+1xj+1(k)−...−ajNxN(k)
高斯-赛德尔迭代法每一次迭代的迭代式为
G a u s s − S e i d e l : x j ( k + 1 ) = b j − a j 1 x 1 ( k + 1 ) − . . . − a j j − 1 x j − 1 ( k + 1 ) − a j j + 1 x j + 1 ( k ) − . . . − a j N x N ( k ) a j j Gauss - Seidel:x_j^{(k + 1)} = \frac{{{b_j} - {a_{j1}}x_1^{(k + 1)} - ... - {a_{jj - 1}}x_{j - 1}^{(k + 1)} - {a_{jj + 1}}x_{j + 1}^{(k)} - ... - {a_{jN}}x_N^{(k)}}}{{{a_{jj}}}} Gauss−Seidel:xj(k+1)=ajjbj−aj1x1(k+1)−...−ajj−1xj−1(k+1)−ajj+1xj+1(k)−...−ajNxN(k)
可以看出,高斯-赛德尔迭代法相较于雅可比迭代法而言,其每次迭代时所用的解都是尽可能新的,而雅可比迭代法则是完全采用上一组近似解的值,所以对于方程组 A X = B AX=B AX=B,高斯-赛德尔迭代法和雅可比迭代法都收敛,且高斯-赛德尔迭代法比雅可比迭代法收敛快。但是有些情况下,可能会出现高斯-赛德尔迭代法不收敛而雅可比迭代法收敛的情况。
决定迭代法是否收敛,是否可用于该方程组,主要需要考虑的其实就是系数矩阵 A A A。对于迭代法的收敛性,定义以下判断其收敛性。
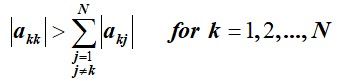
如果矩阵满足此不等式,则称矩阵具有严格对角优势.于是对于雅可比迭代法,对于任意一个初始解向量,向量序列都会收敛到 P P P。
二、实验内容及核心算法代码
1、CAD模型旋转原理实现
由第一节原理部分可知,设 U = [ x y z ] ’ U=[x y z]’ U=[xyz]’是一个笛卡尔坐标系中的三维列向量,设A是一个 3 × 3 3×3 3×3矩阵,那么乘积矩阵 V = A U V=AU V=AU表示空间向量的一个线性变换,其中得到的矩阵U为变换后所表示的三维列向量。并且三个变换矩阵 R x ( α ) {R_x}(\alpha ) Rx(α)、 R y ( β ) {R_y}(\beta ) Ry(β)、 R z ( γ ) {R_z}(\gamma ) Rz(γ)分别实现的功能为绕特定坐标轴旋转。于是,实现CAD模型旋转只需要用定义的变换矩阵乘以列向量即可。
实现CAD模型旋转的步骤如下。
- 定义一个位于第一象限的单位立方体,一个顶点位于原点。8个顶点即8个三维列向量,可以用一个 8 × 3 8×3 8×3矩阵表示,矩阵的每一列表示一个顶点的坐标。 8 × 3 8×3 8×3矩阵记作立方体的坐标矩阵,记为 U U U。
- 定义三个变换矩阵 R x ( α ) {R_x}(\alpha ) Rx(α)、 R y ( β ) {R_y}(\beta ) Ry(β)、 R z ( γ ) {R_z}(\gamma ) Rz(γ),其中三个角度分别为绕 x , y , z x,y,z x,y,z轴旋转的角度。
- 用变换矩阵 R x ( α ) {R_x}(\alpha ) Rx(α)、 R y ( β ) {R_y}(\beta ) Ry(β)、 R z ( γ ) {R_z}(\gamma ) Rz(γ)乘以 U U U,由矩阵的乘法性质可知,得到的新的矩阵 U ' U' U'仍是一个 8 × 3 8×3 8×3矩阵,其每一个列向量表示变换后的对应的立方体8个顶点的坐标。可以通过不同的变换矩阵实现不同的立方体旋转效果,实现CAD模型旋转。
其实现的流程图大致为

以下通过一个实例来进行CAD模型旋转的实验。 - 定义一个位于第一象限的单位立方体,一个顶点位于原点。首先,以角度 π 6 \frac{\pi }{6} 6π沿y轴旋转,然后,以角度 π 4 \frac{\pi }{4} 4π沿z轴旋转,求解旋转后的立方体。
由CAD模型旋转的步骤可知,应当以矩阵 R y ( π 6 ) {R_y}(\frac{\pi }{6}) Ry(6π)、 R z ( π 4 ) {R_z}(\frac{\pi }{4}) Rz(4π)乘以立方体坐标矩阵,从而实现立方体的旋转。其核心算法的函数代码(MATLAB)为:
%输入参数说明
%cor为定义的立方体的坐标矩阵
%Ry,Rz为定义的绕y轴,z轴旋转的变换矩阵
%n为控制动画的采样数
function temp1(cor,Ry,Rz,n)
M=moviein(n);
for i=1:2*n
if(i<=n)
cor=Ry*cor;
set(gca,'ydir','reverse');
plot3(cor(1,:),cor(2,:),cor(3,:));
axis equal;
axis tight;
axis([-1,1.5,-1,1.8,-0.5,1]);
xlabel('x');ylabel('y');zlabel('z');
grid on;
M(i)=getframe;
end
if(i>n)
cor=Rz*cor;
set(gca,'ydir','reverse');
plot3(cor(1,:),cor(2,:),cor(3,:));
axis equal;
axis tight;
axis([-1,1.5,-1,1.8,-0.5,1]);
xlabel('x');ylabel('y');zlabel('z');
grid on;
M(i)=getframe;
end
end
movie(M,1,5);
end
2、三角分解法原理
由 L U LU LU分解法的基本原理可知,一个方阵可分解成两个矩阵的乘积,当给定一些约束后,这些分解将是唯一的。对矩阵进行三角分解实际上只是将矩阵分解成上三角矩阵和下三角矩阵的乘积,这样对任意方程组的求解问题就转化为三角形方程组的求解问题,方便利用回代算法计算。于是其基本过程为:
- 首先对矩阵进行偏序选主元操作。对于第1行开始,将高斯消元法的系数保留在下三角矩阵中的第1列中,并对以下的第k行(除去第k列)施以高斯消元的步骤。得到 A = L U A=LU A=LU。
- 将方程变为 L U X = B LUX=B LUX=B。令 U X = Y UX=Y UX=Y,先利用回代法求解下三角矩阵 L Y = B LY=B LY=B,其回代法是从第一行开始进行。解除Y矩阵。
- 对方程组 U X = Y UX=Y UX=Y进行回代法,其回代法是从最后一行开始执行。得到最终的解 X X X。
以下通过1个实例来进行三角分解法的实验。
- 求解线性方程组AX=B其中A= [ a i j ] N × N {[{a_{ij}}]_{N \times N}} [aij]N×N, [ a i j ] = i j − 1 [{a_{ij}}]{\rm{ = }}{i^{j - 1}} [aij]=ij−1;而且B= [ b i j ] N × 1 {[{b_{ij}}]_{N \times 1}} [bij]N×1, b 11 {b_{11}} b11 = N =N =N,当 i ≥ 2 i≥2 i≥2时, b i 1 = ( i N − 1 ) / ( i − 1 ) {b_{i1}} = ({i^N} - 1)/(i - 1) bi1=(iN−1)/(i−1)。对 N = 3 , 7 , 11 N=3,7,11 N=3,7,11的形况进行分别求解。
由 L U LU LU分解法具体过程可知,仅需要生成矩阵,并对其进行 L U LU LU分解操作,再将其转化为求解两个上三角和下三角的矩阵的回答过程,并判断矩阵是否为奇异矩阵,即可得出解。
其核心代码如下
//first,pivote the matrix by partial pivote
//from the startr to find the pivote,and return the row number
int FindtheMaxrow(float** mat, int startr, int N)
{
float mval = mat[startr][startr];
int maxr = startr;
//find the maxvalue row
for (int i = startr + 1; i < N; ++i)
{
if (mval < mat[i][startr])
{
maxr = i;
}
}
return maxr;
}
//the function is to exchange the p and k row of the matrix and the B vector
void ExchangewithMaxrow(float** mat, float* B, int p, int k, int N)
{
float tempv;
for (int i = 0; i < N; ++i)
{
tempv = mat[p][i];
mat[p][i] = mat[k][i];
mat[k][i] = tempv;
}
tempv = B[p];
B[p] = B[k];
B[k] = tempv;
}
//this is a integrate function to finish the partial pivote task
void PartialPivotingmethodtoLinearsystem(float** mat, float* B, float* X, int N)
{
int maxr;
//finish the pivote work
for (int i = 0; i < N - 1; ++i)
{
//find the max row of i row
maxr = FindtheMaxrow(mat, i, N);
if (maxr != i)
{
//exchange them
ExchangewithMaxrow(mat, B, i, maxr, N);
}
}
}
// do the LU fac
void LUFacMatrix(float** mat, int n)
{
float mrp;
for (int i = 0; i < n - 1; ++i)
{
for (int j = i + 1; j < n; ++j)
{
mrp = mat[j][i] / mat[i][i];
mat[j][i] = mrp;
for (int c = i + 1; c < n; ++c)
{
mat[j][c] -= mat[i][c] * mrp;
}
}
}
}
//as become the LUX=B,let Y=UX,solve the LY=B
void solveLYlinearsystem(float** L, float* Y, float* B, int n)
{
float sval;
//the first row
Y[0] = B[0];
//solve the 2,3,4... row
for (int r = 1; r < n; ++r)
{
sval = 0;
for (int c = 0; c < r; ++c)
{
sval += L[r][c] * Y[c];
}
Y[r] = B[r] - sval;
}
}
//as the Y matrix has been solved,solve the UX=Y
void solveUXlinearsystem(float** U, float* X, float* Y, int n)
{
float sval;
for (int r = n - 1; r >= 0; --r)
{
sval = 0;
for (int c = r + 1; c < n; ++c)
{
sval += U[r][c] * X[c];
}
X[r] = (Y[r] - sval) / U[r][r];
}
}
//the LU matrix has the L and U,and when be used,they are not clash
void SolveLinearsystembyLU(float** LU, float* X, float* B, int n)
{
float* Y;
Y = MallocArr(n);
//get the Y matrix
solveLYlinearsystem(LU, Y, B, n);
//get the Y matrix
solveUXlinearsystem(LU, X, Y, n);
FreeArr(Y);
}
3、雅可比迭代法和高斯-赛德尔迭代法实现
由雅可比迭代法和高斯-赛德尔迭代法的基本原理可知,给定一个初始的近似解,利用线性方程组进行迭代,每次迭代产生一个比原来解更接近精确解的向量,直到最终解向量收敛于精确解向量,即小于给定精度范围。以下通过1个实例来进行雅可比迭代法和高斯-赛德尔迭代法的实验。
设由两个带状稀疏矩阵

充分利用矩阵的稀疏特性求解方程组。其基本过程如下:
- 写出每一行的迭代公式,因为矩阵具有稀疏性,所以每一个迭代公式仅仅只用写出前后几个元素,从而大大提高迭代效率。
- 设置初始解向量X=[1,1,1,1…1],将X带入迭代公式,分别利用雅可比迭代法和高斯-赛德尔迭代法进行迭代计算。
- 设置误差精度为eps=1e-7,通过第i个和i+1个解向量的范数大小来判断结束的条件,并且设置最大迭代次数,以免发散序列一直进行。最终输出结果。
其核心代码如下
//求解X1和X2向量的范数,n为向量的维数
float ErrofNorm(float* X1, float* X2, const int n)
{
float norm = 0;
for (int i = 0; i < n; ++i)
{
norm += (X1[i] - X2[i]) * (X1[i] - X2[i]);
}
return sqrt(norm);
}
//A,B,X为方程组中的AX=B值,MaxIter为最大迭代次数,nIter为迭代次数,n为矩阵维数,eps为设置的误差
void Itermethodfor365_3byJacobi(float **A,float *X,float *B,const int MaxIter,int &nIter,const int n,const float eps)
{
float* preX;
float err;
preX = MallocArr(n);
do
{
if (nIter > MaxIter)
{
cout << "cannot find the precise solution within the max iteration time" << endl;
return;
}
//let preX store the old num
memcpy(preX, X, n * sizeof(float));//the third parameter is the byte size
//the first and the last row only contain two element
X[0] = (B[0] - A[0][1] * X[1]) / A[0][0];
X[n - 1] = (B[n - 1] - A[n - 1][n - 2] * X[n - 2]) / A[n - 1][n - 1];
float valf, valb;
//every row only i-1,i,i+1 column have element,so just add two number every step
//it can make use of the sparse nature of the matrix
for (int i = 1; i < n - 1; ++i)
{
//sum the front and back number of the nth solution
valf = A[i][i-1]*preX[i-1], valb = A[i][i + 1] * preX[i + 1];
X[i] = (B[i] - valf - valb) / A[i][i];
}
err = ErrofNorm(X, preX, n);
++nIter;
} while (err > eps);
//remember to free the allocated memory
FreeArr(preX);
}
//A,B,X为方程组中的AX=B值,MaxIter为最大迭代次数,nIter为迭代次数,n为矩阵维数,eps为设置的误差
void Itermethodfor365_3byGauss_Seidel(float** A, float* X, float* B, const int MaxIter, int& nIter, const int n, const float eps)
{
float* preX;
float err;
preX = MallocArr(n);
do
{
if (nIter > MaxIter)
{
cout << "cannot find the precise solution within the max iteration time" << endl;
return;
}
//let preX store the old num
memcpy(preX, X, n * sizeof(float));//the third parameter is the byte size
//the first and the last row only contain two element
X[0] = (B[0] - A[0][1] * X[1]) / A[0][0];
float valf, valb;
//every row only i-1,i,i+1 column have element,so just add two number every step
//it can make use of the sparse nature of the matrix
for (int i = 1; i < n - 1; ++i)
{
//sum the front and back number of the nth solution
//use the newest coordinate,instead of preX[i-1]
valf = A[i][i - 1] * X[i - 1], valb = A[i][i + 1] * X[i + 1];
X[i] = (B[i] - valf - valb) / A[i][i];
}
//move this step to the last to use the newest coordinate
X[n - 1] = (B[n - 1] - A[n - 1][n - 2] * X[n - 2]) / A[n - 1][n - 1];
err = ErrofNorm(X, preX, n);
++nIter;
} while (err > eps);
//remember to free the allocated memory
FreeArr(preX);
三、实验数据结果分析
1、CAD模型旋转
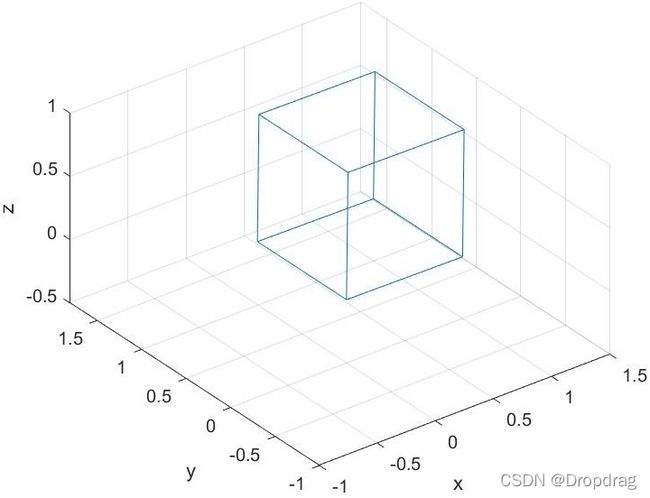
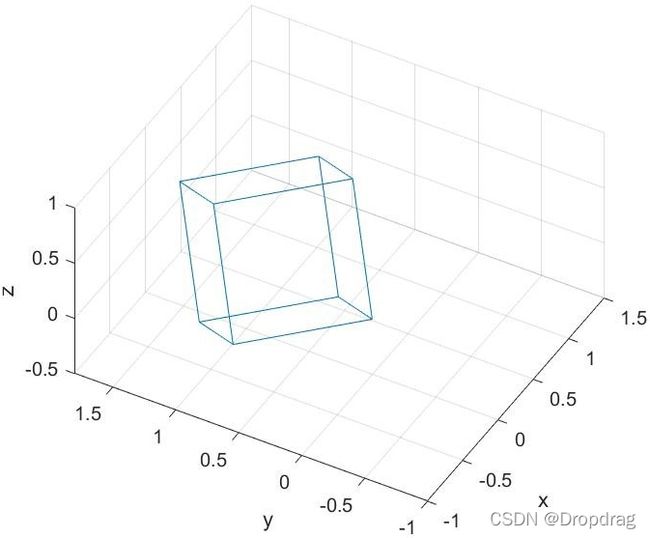
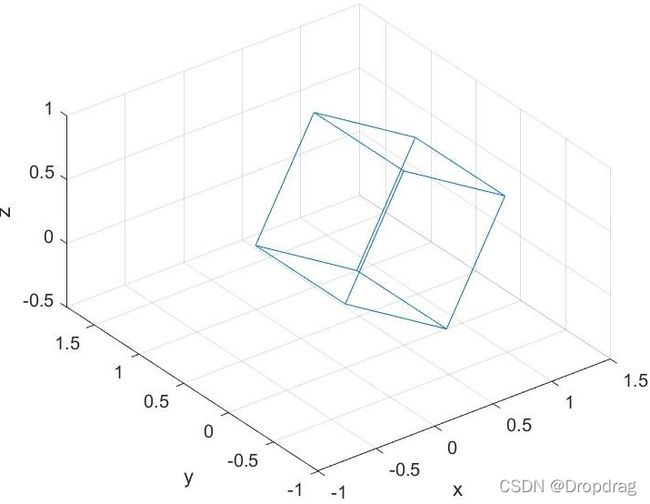
利用旋转变换矩阵可以实现对图形的处理,此实例为简单的绕固定转轴旋转,通过仔细设计变换矩阵,可以实现图形的平移、伸缩和更加复杂的变换,而且通过矩阵具有高性能可并行计算的特点,因此在计算机图形学中可以更加高效的控制图像,实现更加复杂的变换。
三角分解法
由实例结果可知,通过对矩阵进行LU分解,得到的矩阵不仅仅具有准确度高的特点,而且能够提高计算速度。其中,实例一中当N=11时计算结果与前面两组结果出现明显差异,其原因可能是由于系数矩阵的主对角元没有进行按比例偏序选主元步骤,导致由于截断误差的存在使得传播误差变大,使结果失真。在实列二计算矩阵行列式中LU分解法表现出良好的特性,得到的结果完全正确。所以当进行大规模或大数值的矩阵运算时,应当先对矩阵进行可逆性的判断以及偏序选主元法的操作,以此来降低在使用LU分解法过程中造成的误差的放大。
实验数据已上传至文末资源,请大家自行下载!
雅可比迭代法和高斯-赛德尔迭代法
由结果可以看出,在给定最大迭代次数 M a x I t e r = 100 MaxIter=100 MaxIter=100,精度范围 e p s = 1 e − 9 eps=1e-9 eps=1e−9的条件下,雅可比迭代法和高斯-赛德尔迭代法都具有特别好的收敛性,而且两种方法的迭代结果一致,说明二者在求解线性方程组中均具有明显作用。然而实际上,记录二者的迭代次数会发现,在实例一中雅可比迭代法的迭代次数为100,而高斯-赛德尔迭代法的迭代次数为3;在实例二中雅可比迭代法的迭代次数为26,而高斯-赛德尔迭代法的迭代次数为1。于是可以看出在二者均收敛的情况下,高斯-赛德尔迭代法比雅可比迭代法具有更快的收敛速度。所以在实际计算中,当保证了系数矩阵具有严格对角优势的前提下,应当尽可能选用高斯-赛德尔迭代法以获得更小的时间复杂度与计算时间。
四、结论
在基于矩阵的运算性质上,可以通过设计矩阵进行空间的变换;在计算线性方程组 A X = B AX=B AX=B的过程中,我们也可以利用特殊矩阵的性质进行矩阵的初等变换,在不改变矩阵的解的情况下,让矩阵化简成易于迭代计算的形式。所以,掌握矩阵的特殊变换以及通过设计特殊的矩阵对于高性能的矩阵并行计算具有重大的意义,我们可以通过基于矩阵运算的性质来计算更为庞大的方程组,并且通过合理的判据条件以及计算过程得到更为精确的数值解。
声明:本系列《数值计算方法》所有章节源代码均为作者编写,大家可以自行下载,仅供学习交流使用,欢迎大家评论留言或者私信交流,请勿用于任何商业行为。其中,各章实验数据结果也在资源链接中,大家可以自行实验对照,欢迎大家批评指正!文件中每个算法均由作者进行初步测试,部分算法可直接用于工程开发作为模块参考。
各章算法源代码(C++)