运动学与雅可比矩阵举例
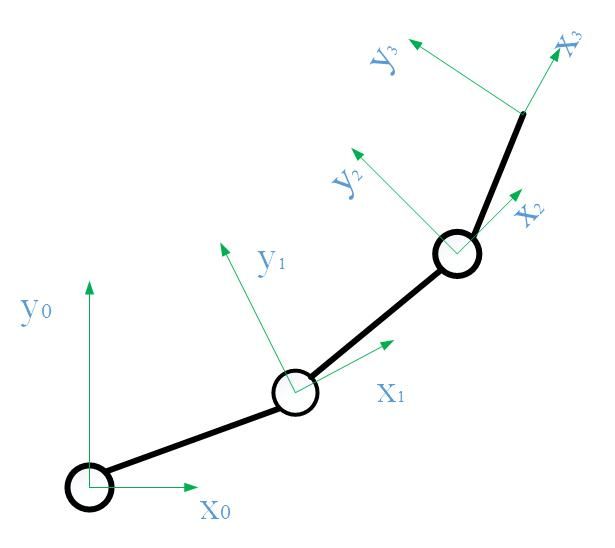
以三连杆平面机械臂为例,来说明D-H矩阵和雅可比矩阵的求法,并且比较后置法和前置法的异同和运动学末端位姿的一致性和雅可比矩阵的一致性。
一、 后置法。
如图建立个连杆的坐标系,D-H参数如下表所示:
| 连杆 | a | alpha | d | theta |
|---|---|---|---|---|
| 1 | a1 | 0 | 0 | theta1 |
| 2 | a2 | 0 | 0 | theta2 |
| 3 | a3 | 0 | 0 | theta3 |
对应的齐次矩阵是:
Ti−1i(θi)=⎡⎣⎢⎢⎢cisi00−sici000010aiciaisi01⎤⎦⎥⎥⎥ T i i − 1 ( θ i ) = [ c i − s i 0 a i c i s i c i 0 a i s i 0 0 1 0 0 0 0 1 ]
(3)、运动学方程。
To3(q)=⎡⎣⎢⎢⎢c123s12300−s123c123000010a1c1+a1c12+a1c123a1s1+a1s12+a1s12301⎤⎦⎥⎥⎥ T 3 o ( q ) = [ c 123 − s 123 0 a 1 c 1 + a 1 c 12 + a 1 c 123 s 123 c 123 0 a 1 s 1 + a 1 s 12 + a 1 s 123 0 0 1 0 0 0 0 1 ]
(4)、雅可比矩阵。
To1(q)=⎡⎣⎢⎢⎢c1s100−s1c1000010a1c1a1s101⎤⎦⎥⎥⎥ T 1 o ( q ) = [ c 1 − s 1 0 a 1 c 1 s 1 c 1 0 a 1 s 1 0 0 1 0 0 0 0 1 ]
T02(q)=⎡⎣⎢⎢⎢c12s1200−s12c12000010a1c1+a1c12a1s1+a1s1201⎤⎦⎥⎥⎥ T 2 0 ( q ) = [ c 12 − s 12 0 a 1 c 1 + a 1 c 12 s 12 c 12 0 a 1 s 1 + a 1 s 12 0 0 1 0 0 0 0 1 ]
根据以上方程,可以得到:
z0=z1=z2=z3=⎡⎣⎢001⎤⎦⎥ z 0 = z 1 = z 2 = z 3 = [ 0 0 1 ]
p0=⎡⎣⎢000⎤⎦⎥ p 0 = [ 0 0 0 ]
p1=⎡⎣⎢a1c1a1s10⎤⎦⎥ p 1 = [ a 1 c 1 a 1 s 1 0 ]
p2=⎡⎣⎢a1c1+a1c12a1s1+a1s120⎤⎦⎥ p 2 = [ a 1 c 1 + a 1 c 12 a 1 s 1 + a 1 s 12 0 ]
p3=⎡⎣⎢a1c1+a1c12+a1c123a1s1+a1s12+a1s1230⎤⎦⎥ p 3 = [ a 1 c 1 + a 1 c 12 + a 1 c 123 a 1 s 1 + a 1 s 12 + a 1 s 123 0 ]
根据旋转关节的雅可比计算公式,
JPi=[Zi−1∗(Pe−Pi−1)Zi−1] J P i = [ Z i − 1 ∗ ( P e − P i − 1 ) Z i − 1 ]
可以得到:
J=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢−s1(a2c2+a3c23)c1(a2c2+a3c23)0001−c1(a2s2+a3s23)−s1(a2s2+a3s23)a2c2+a3c23s1−c10−a3c1s23−a3s1s23a3c23s1−c10⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥ J = [ − s 1 ( a 2 c 2 + a 3 c 23 ) − c 1 ( a 2 s 2 + a 3 s 23 ) − a 3 c 1 s 23 c 1 ( a 2 c 2 + a 3 c 23 ) − s 1 ( a 2 s 2 + a 3 s 23 ) − a 3 s 1 s 23 0 a 2 c 2 + a 3 c 23 a 3 c 23 0 s 1 s 1 0 − c 1 − c 1 1 0 0 ]
二、 前置法。
如图建立个连杆的坐标系,D-H参数如下表所示:
| 连杆 | a | alpha | d | theta |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | theta1 |
| 2 | a1 | 0 | 0 | theta2 |
| 3 | a2 | 0 | 0 | theta3 |
| 4 | a3 | 0 | 0 |
对应的齐次矩阵是:
To1(θ1)=⎡⎣⎢⎢⎢c1s100−s1c10000100001⎤⎦⎥⎥⎥ T 1 o ( θ 1 ) = [ c 1 − s 1 0 0 s 1 c 1 0 0 0 0 1 0 0 0 0 1 ]
Ti−1i(θi)=⎡⎣⎢⎢⎢cisi00−sici000010ai−1ciai−1si01⎤⎦⎥⎥⎥i=2,3 T i i − 1 ( θ i ) = [ c i − s i 0 a i − 1 c i s i c i 0 a i − 1 s i 0 0 1 0 0 0 0 1 ] i = 2 , 3
T34(θi)=⎡⎣⎢⎢⎢100001000010a3001⎤⎦⎥⎥⎥ T 4 3 ( θ i ) = [ 1 0 0 a 3 0 1 0 0 0 0 1 0 0 0 0 1 ]
(3)、运动学方程。
To4(q)=⎡⎣⎢⎢⎢c123s12300−s123c123000010a1c1+a1c12+a1c123a1s1+a1s12+a1s12301⎤⎦⎥⎥⎥ T 4 o ( q ) = [ c 123 − s 123 0 a 1 c 1 + a 1 c 12 + a 1 c 123 s 123 c 123 0 a 1 s 1 + a 1 s 12 + a 1 s 123 0 0 1 0 0 0 0 1 ]
(4)、雅可比矩阵。
To1(θ1)=⎡⎣⎢⎢⎢c1s100−s1c10000100001⎤⎦⎥⎥⎥ T 1 o ( θ 1 ) = [ c 1 − s 1 0 0 s 1 c 1 0 0 0 0 1 0 0 0 0 1 ]
To2(q)=⎡⎣⎢⎢⎢c1s100−s1c1000010a1c1a1s101⎤⎦⎥⎥⎥ T 2 o ( q ) = [ c 1 − s 1 0 a 1 c 1 s 1 c 1 0 a 1 s 1 0 0 1 0 0 0 0 1 ]
T03(q)=⎡⎣⎢⎢⎢c12s1200−s12c12000010a1c1+a1c12a1s1+a1s1201⎤⎦⎥⎥⎥ T 3 0 ( q ) = [ c 12 − s 12 0 a 1 c 1 + a 1 c 12 s 12 c 12 0 a 1 s 1 + a 1 s 12 0 0 1 0 0 0 0 1 ]
根据以上方程,可以得到:
z0=z1=z2=z3=z4=⎡⎣⎢001⎤⎦⎥ z 0 = z 1 = z 2 = z 3 = z 4 = [ 0 0 1 ]
p0=p1=⎡⎣⎢000⎤⎦⎥ p 0 = p 1 = [ 0 0 0 ]
p2=⎡⎣⎢a1c1a1s10⎤⎦⎥ p 2 = [ a 1 c 1 a 1 s 1 0 ]
p3=⎡⎣⎢a1c1+a1c12a1s1+a1s120⎤⎦⎥ p 3 = [ a 1 c 1 + a 1 c 12 a 1 s 1 + a 1 s 12 0 ]
p4=⎡⎣⎢a1c1+a1c12+a1c123a1s1+a1s12+a1s1230⎤⎦⎥ p 4 = [ a 1 c 1 + a 1 c 12 + a 1 c 123 a 1 s 1 + a 1 s 12 + a 1 s 123 0 ]
根据旋转关节的雅可比计算公式,
JPi=[Zi∗(Pe−Pi)Zi] J P i = [ Z i ∗ ( P e − P i ) Z i ]
可以得到:
J=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢−s1(a2c2+a3c23)c1(a2c2+a3c23)0001−c1(a2s2+a3s23)−s1(a2s2+a3s23)a2c2+a3c23s1−c10−a3c1s23−a3s1s23a3c23s1−c10⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥ J = [ − s 1 ( a 2 c 2 + a 3 c 23 ) − c 1 ( a 2 s 2 + a 3 s 23 ) − a 3 c 1 s 23 c 1 ( a 2 c 2 + a 3 c 23 ) − s 1 ( a 2 s 2 + a 3 s 23 ) − a 3 s 1 s 23 0 a 2 c 2 + a 3 c 23 a 3 c 23 0 s 1 s 1 0 − c 1 − c 1 1 0 0 ]
三、 比较说明。
通过比较可以发现,后置法和前置法计算的运动学方程和雅可比矩阵是相同的。
四、 参考文献
1) John J Craig, 机器人学导论(第三版),机械工业出版社,2006.6.
2) Saeed B.Niku 等,机器人学导论——分析、系统及应用,电子工业出版社,2004.1.
3) Bruno Siciliano 等,机器人学 建模、规划与控制,西安交通大学出版社,2013.11.