基础算法思想:贪心
一、贪心的基本概念:
贪心是最容易理解的基础算法思想:把整个问题分解成多个步骤,在每个步骤都选取当前步骤的最优方案,直到所有的步骤结束;在每一步都不考虑对后续步骤的影响,在后续步骤中也不再回头改变前面的选择。简单的说,其思想就是“走一步看一步”“目光短浅”。
贪心应用广泛。例如图论中的最小生成树算法、单源最短路径算法Dijkstra。
二、例题:
例题1:LeetCode11.盛最多水的容器
1、题目:
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i,height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
提示:
n == height.length2 <= n <= 1050 <= height[i] <= 104
2、题目分析:
核心:双指针 + 贪心
头指针表示左边界位置,尾指针表示右边界位置。
每次比较左右边界高度:若左边界高度<右边界高度,最大面积=max(最大面积,左边界高度×当前宽度),左边界右移;
否则最大面积=max(最大面积,右边界高度×当前宽度),右边界左移。
3、参考代码:
class Solution {
public:
int maxArea(vector& height) {
int l=0, r=height.size()-1,Max=0;
while(l 例题2:LeetCode45.跳跃游戏II
1、题目:
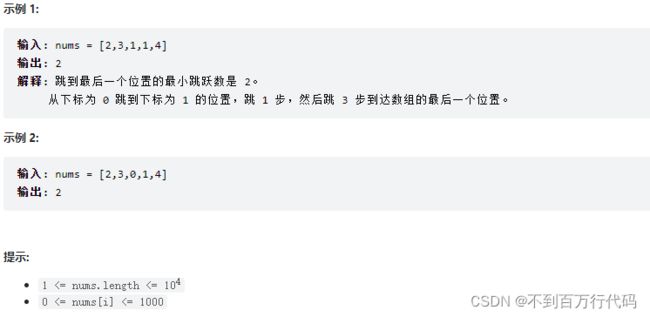
给你一个非负整数数组 nums ,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
假设你总是可以到达数组的最后一个位置。
2、题目分析:
(1)维护一个max表示step步数下能够到达的最远的位置
(2)每次遍历当前位置到max位置,并更新max
(3)本题也可以用动态规划的思想来做(在此不做赘述)
3、参考代码:
class Solution {
public:
int jump(vector& nums) {
int n = nums.size();
if(n == 1) return 0;
//max表示step步数下能跳到的最远距离
int max = nums[0];
int step = 1;
for(int i=0;i 附:
本来是打算出下面这个知识点的相关题的,但是由于本人水平有限,搞到一半发现自己好像理解不了,所以换了一个知识点,如果有感兴趣的同学可以写一下。
1、知识点:线段树之点修改
2、题目链接:2182 -- Lost Cows
题目描述(Description):
N (2 <= N <= 8,000) cows have unique brands in the range 1..N. In a spectacular display of poor judgment, they visited the neighborhood 'watering hole' and drank a few too many beers before dinner. When it was time to line up for their evening meal, they did not line up in the required ascending numerical order of their brands.
Regrettably, FJ does not have a way to sort them. Furthermore, he's not very good at observing problems. Instead of writing down each cow's brand, he determined a rather silly statistic: For each cow in line, he knows the number of cows that precede that cow in line that do, in fact, have smaller brands than that cow.
Given this data, tell FJ the exact ordering of the cows.
( N (2 <= N <= 8,000) 头奶牛在 1..N 范围内有独特的品牌。他们在晚饭前参观了附近的“水坑”,并喝了太多啤酒,表现出判断力差的惊人表现。到了排队吃晚饭的时候,他们没有按照品牌要求的升序排列。
遗憾的是,FJ 没有办法对它们进行排序。此外,他不太善于观察问题。他没有写下每头奶牛的品牌,而是确定了一个相当愚蠢的统计数据:对于排队的每头奶牛,他知道排在该奶牛之前的奶牛的数量,事实上,这些奶牛的品牌比那头奶牛小。
给定这些数据,告诉 FJ 奶牛的确切顺序。)
Input
* Line 1: A single integer, N
* Lines 2..N: These N-1 lines describe the number of cows that precede a given cow in line and have brands smaller than that cow. Of course, no cows precede the first cow in line, so she is not listed. Line 2 of the input describes the number of preceding cows whose brands are smaller than the cow in slot #2; line 3 describes the number of preceding cows whose brands are smaller than the cow in slot #3; and so on.
(* 第 1 行:单个整数,N
* 第 2..N 行:这些 N-1 行描述了排在给定奶牛之前且品牌小于该奶牛的奶牛数量。当然,没有奶牛排在第一头奶牛之前,所以她没有被列出。输入的第 2 行描述了品牌小于插槽 #2 中的奶牛的前面奶牛的数量;第 3 行描述了品牌小于槽#3 中的奶牛的前面奶牛的数量;等等 )
Output
* Lines 1..N: Each of the N lines of output tells the brand of a cow in line. Line #1 of the output tells the brand of the first cow in line; line 2 tells the brand of the second cow; and so on.
(* 第 1..N 行:N 行输出中的每一行都说明了一头母牛的品牌。输出的第 1 行告诉第一头奶牛的品牌;第 2 行告诉第二头牛的品牌;等等。)
Sample Input
5 1 2 1 0
Sample Output
2 4 5 3 1
3、参考代码:
(1)暴力法:
(2)用完全二叉树实现线段树