数组相关算法题(一)
数组相关算法题:
1 、二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示:
你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。
class Solution {
public int search(int[] nums, int target) {
int left = 0, right = nums.length - 1,mid = 0;
while(left <= right){
mid = left + ((right -left) >> 1);
if(nums[mid] == target){
return mid;
}else if(nums[mid] > target){
right = mid - 1;
}else{
left = mid + 1;
}
}
return -1;
}2、移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以「引用」方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参作任何拷贝
int len = removeElement(nums, val);
// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
print(nums[i]);
}
示例 1:
输入:nums = [3,2,2,3], val = 3
输出:2, nums = [2,2]
解释:函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 ,而 nums = [2,2,3,3] 或 nums = [2,2,0,0],也会被视作正确答案。
示例 2:
输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,4,0,3]
解释:函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。
提示:
0 <= nums.length <= 100
0 <= nums[i] <= 50
0 <= val <= 100
此题使用双指针:快慢指针
class Solution {
public int removeElement(int[] nums, int val) {
int fastIndex=0,slowIndex=0;
for(fastIndex = 0 ; fastIndex < nums.length ; fastIndex ++ ){
if(nums[fastIndex] != val){
nums[slowIndex] = nums[fastIndex];
slowIndex ++;
}
}
return slowIndex;
}
}3、长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
提示:
1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105
双for循环
时间复杂度为O(n^2)的写法
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int sum ,result = Integer.MAX_VALUE,sublength = 0 ;
for(int i = 0 ; i < nums.length; i++){
sum = 0;
for(int j = i; j < nums.length; j++){
sum+=nums[j];
if(sum >= target){
sublength = j - i + 1;
result = result > sublength ? sublength : result;
break;
}
}
}
return result == Integer.MAX_VALUE ? 0 : result;
}
}操作数组的滑动窗口写法
时间复杂度为O(n)的写法
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int sum=0 ,result = Integer.MAX_VALUE,sublength = 0 ;int j = 0;
for(int i = 0 ; i < nums.length; i++){
sum += nums[i];
while(sum >= target){
sublength = i - j + 1;
result = result > sublength ? sublength : result;
sum-=nums[j++];
}
}
return result == Integer.MAX_VALUE ? 0 : result;
}
}4、螺旋矩阵
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
![]()
示例 2:输入:n = 1
输出:[[1]]
提示:
1 <= n <= 20
class Solution {
public int[][] generateMatrix(int n) {
int[][] result = new int[n][n];
int loop = n/2 , starX=0,starY=0,count = 1,offset=1;
while(loop > 0){
int i = starX,y = starY;
//最上边从左到右
for( ; y < n +starY - offset ; y++){
result[i][y] = count ++;
}
//最右边上从到下
for( ;i < n +starX - offset;i++ ){
result[i][y] = count ++;
}
//最下边从右到左
for( ; y > starY; y--){
result[i][y] = count ++;
}
//最z左边从下到上
for( ; i > starX ; i--){
result[i][y] = count ++;
}
loop --;
starX ++;
starY ++;
offset += 2;
}
if(n % 2 == 1){
int mid = n / 2;
result[mid][mid] = count ++;
}
return result;
}
}5 、删除有序数组中的重复项
给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以「引用」方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参做任何拷贝
int len = removeDuplicates(nums);
// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
print(nums[i]);
}
示例 1:
输入:nums = [1,1,2]
输出:2, nums = [1,2]
解释:函数应该返回新的长度 2 ,并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
示例 2:
输入:nums = [0,0,1,1,1,2,2,3,3,4]
输出:5, nums = [0,1,2,3,4]
解释:函数应该返回新的长度 5 , 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
class Solution {
public int removeDuplicates(int[] nums) {
if( nums == null || nums.length == 0){
return 0;
}
int slow = 0;
for(int fast = 0 ; fast < nums.length -1 ; fast ++){
if(nums[fast] != nums[fast+1]){
nums[++slow] = nums[fast+1];
}
}
return slow + 1 ;
}
}6、搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
你可以假设数组中无重复元素。
示例 1:
输入: [1,3,5,6], 5
输出: 2
示例 2:
输入: [1,3,5,6], 2
输出: 1
示例 3:
输入: [1,3,5,6], 7
输出: 4
示例 4:
输入: [1,3,5,6], 0
输出: 0
class Solution {
public int searchInsert(int[] nums, int target) {
for(int i = 0 ; i < nums.length ; i++){
if(nums[i] >= target){
return i;
}
}
return nums.length;
}
}7、最大子序列和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [0]
输出:0
示例 4:
输入:nums = [-1]
输出:-1
示例 5:
输入:nums = [-100000]
输出:-100000
解题思路:当前N 的值与前面K个值的和相加,如若前面k个值的和 < 0 ,则N 的值与前k个值的和相加是没有意义的,故求和的值会是从当前值算起。只有与正数值相加 才会得到更大的值
class Solution {
public int maxSubArray(int[] nums) {
int res = nums[0];
int sum = 0;
for (int num : nums) {
if (sum > 0)
sum += num;
else
sum = num;
res = Math.max(res, sum);
}
return res;
}
}8、加一
给定一个由 整数 组成的 非空 数组所表示的非负整数,在该数的基础上加一。
最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。
你可以假设除了整数 0 之外,这个整数不会以零开头。
示例 1:
输入:digits = [1,2,3]
输出:[1,2,4]
解释:输入数组表示数字 123。
示例 2:
输入:digits = [4,3,2,1]
输出:[4,3,2,2]
解释:输入数组表示数字 4321。
示例 3:
输入:digits = [0]
输出:[1]
class Solution {
public int[] plusOne(int[] digits) {
for(int i = digits.length -1 ; i >= 0 ; i--){
if(digits[i] != 9){
digits[i] ++;
return digits;
}
digits[i] = 0;
}
int[] newDigits = new int[digits.length +1];
newDigits[0] = 1;
return newDigits;
}
}9、将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
示例 1:
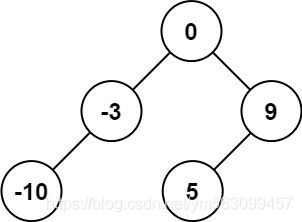
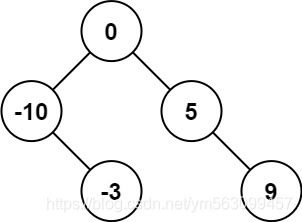
输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
示例 2:
输入:nums = [1,3]
输出:[3,1]
解释:[1,3] 和 [3,1] 都是高度平衡二叉搜索树。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
return getBST(nums,0,nums.length -1);
}
public static TreeNode getBST(int[] nums,int left,int right){
if(left > right){
return null;
}
TreeNode treeNode = new TreeNode();
int mid = left + ((right - left)/2 );
int midval = nums[mid];
treeNode.val = midval ;
treeNode.left = getBST(nums,left,mid -1);
treeNode.right = getBST(nums,mid+1,right);
return treeNode;
}
}10、杨辉三角
给定一个非负整数 numRows,生成杨辉三角的前 numRows 行。
在杨辉三角中,每个数是它左上方和右上方的数的和。
示例:
输入: 5
输出:
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]
class Solution {
public List> generate(int numRows) {
List> generateList = new ArrayList<>();
for(int i = 0 ; i < numRows ; i++){
List list = new ArrayList<>();
for(int j = 0 ; j <= i; j++){
if(j == 0 || j == i) {
list.add(1);
}else{
list.add(generateList.get(i-1).get(j-1)+generateList.get(i-1).get(j));
}
}
generateList.add(list);
}
return generateList;
}
} 11、杨辉三角2
给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行。
在杨辉三角中,每个数是它左上方和右上方的数的和。
示例:
输入: 3
输出: [1,3,3,1]
进阶:
你可以优化你的算法到 O(k) 空间复杂度吗?
class Solution {
public List getRow(int rowIndex) {
List rowIndexList = new ArrayList();
rowIndexList.add(1);
if(rowIndex == 0){
return rowIndexList;
}
List preRowList = getRow(rowIndex - 1);
for(int i = 0 ; i < preRowList.size() - 1; i ++){
rowIndexList.add(preRowList.get(i) + preRowList.get(i+1));
}
rowIndexList.add(1);
return rowIndexList;
}
} 12、买股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
class Solution {
public int maxProfit(int[] prices) {
int max = 0;
int min = prices[0];
for(int i = 1 ; i < prices.length ; i++){
if(prices[i] < min){
min = prices[i];
}else{
max =Math.max(max,prices[i] - min);
}
}
return max;
}
}13、买卖股票的最佳时机2
给定一个数组 prices ,其中 prices[i] 是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: prices = [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: prices = [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: prices = [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
class Solution {
public int maxProfit(int[] prices) {
int sum = 0;
for(int i =1 ; i < prices.length ; i ++){
int differ = prices[i] - prices[i -1] ;
if(differ > 0){
sum += differ;
}
}
return sum;
}
}14、只出现一次的数字
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
输入: [2,2,1]
输出: 1
示例 2:
输入: [4,1,2,1,2]
输出: 4
使用异或的方式处理
4^1^2^1^2 相当于 (1^1)^(2^2)^4,(1^1)=0 ,(2^2) = 0 ,0^X = X;
class Solution {
public int singleNumber(int[] nums) {
int result = nums[0];
for(int i = 1 ; i < nums.length ; i++){
result = result^nums[i];
}
return result;
}
}15、 两数之和 输入有序数组
给定一个已按照 升序排列 的整数数组 numbers ,请你从数组中找出两个数满足相加之和等于目标数 target 。
函数应该以长度为 2 的整数数组的形式返回这两个数的下标值。numbers 的下标 从 1 开始计数 ,所以答案数组应当满足 1 <= answer[0] < answer[1] <= numbers.length 。
你可以假设每个输入只对应唯一的答案,而且你不可以重复使用相同的元素。
示例 1:
输入:numbers = [2,7,11,15], target = 9
输出:[1,2]
解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。
示例 2:
输入:numbers = [2,3,4], target = 6
输出:[1,3]
示例 3:
输入:numbers = [-1,0], target = -1
输出:[1,2]
class Solution {
public int[] twoSum(int[] numbers, int target) {
int i = 0, j = numbers.length - 1; //初始化左右指针
while(i <= j) {
if(numbers[i] + numbers[j] == target) //和等于目标值
return new int[]{i + 1, j + 1};
else if(numbers[i] + numbers[j] < target)
//和小于目标值,我们将左指针往右移,使得和变大
i++;
else //大于目标值,我们将右指针往左移,使得和变小
j--;
}
return new int[0];
}
}16、 多数元素
给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:[3,2,3]
输出:3
示例 2:
输入:[2,2,1,1,1,2,2]
输出:2
进阶:
尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。
使用摩尔算法 :
class Solution {
public int majorityElement(int[] nums) {
int count = 1;
int result = nums[0];
for(int i = 1 ;i < nums.length ; i++){
if(nums[i] == result){
count ++;
}else{
count --;
}
if(count == 0){
result = nums[i];
count=1;
}
}
return result;
}
}17、 存在重复元素
给定一个整数数组,判断是否存在重复元素。
如果存在一值在数组中出现至少两次,函数返回 true 。如果数组中每个元素都不相同,则返回 false 。
示例 1:
输入: [1,2,3,1]
输出: true
示例 2:
输入: [1,2,3,4]
输出: false
示例 3:
输入: [1,1,1,3,3,4,3,2,4,2]
输出: true
方式一
class Solution {
public boolean containsDuplicate(int[] nums) {
return Arrays.stream(nums).distinct().count() != nums.length;
}
}方式二
class Solution {
public boolean containsDuplicate(int[] nums) {
Map map = new HashMap();
for(int i = 0 ; i < nums.length ; i++){
if(map.containsKey(nums[i])){
return true;
}else{
map.put(nums[i],i);
}
}
return false;
}
}方式三
class Solution {
public boolean containsDuplicate(int[] nums) {
Set set = new HashSet<>();
for(int i = 0 ; i < nums.length ; i++){
set.add(nums[i]);
}
if(set.size() == nums.length) return false;
return true;
}
} 18、存在重复元素2
给定一个整数数组和一个整数 k,判断数组中是否存在两个不同的索引 i 和 j,使得 nums [i] = nums [j],并且 i 和 j 的差的 绝对值 至多为 k。
示例 1:
输入: nums = [1,2,3,1], k = 3
输出: true
示例 2:
输入: nums = [1,0,1,1], k = 1
输出: true
示例 3:
输入: nums = [1,2,3,1,2,3], k = 2
输出: false
class Solution {
public boolean containsNearbyDuplicate(int[] nums, int k) {
Map map = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
if(map.containsKey(nums[i]) && Math.abs(map.get(nums[i]) - i ) <= k){
return true;
}else{
map.put(nums[i],i);
}
}
return false;
}
} 19、丢失的数字
给定一个包含 [0, n] 中 n 个数的数组 nums ,找出 [0, n] 这个范围内没有出现在数组中的那个数。
进阶:
你能否实现线性时间复杂度、仅使用额外常数空间的算法解决此问题?
示例 1:
输入:nums = [3,0,1]
输出:2
解释:n = 3,因为有 3 个数字,所以所有的数字都在范围 [0,3] 内。2 是丢失的数字,因为它没有出现在 nums 中。
示例 2:
输入:nums = [0,1]
输出:2
解释:n = 2,因为有 2 个数字,所以所有的数字都在范围 [0,2] 内。2 是丢失的数字,因为它没有出现在 nums 中。
示例 3:
输入:nums = [9,6,4,2,3,5,7,0,1]
输出:8
解释:n = 9,因为有 9 个数字,所以所有的数字都在范围 [0,9] 内。8 是丢失的数字,因为它没有出现在 nums 中。
示例 4:
输入:nums = [0]
输出:1
解释:n = 1,因为有 1 个数字,所以所有的数字都在范围 [0,1] 内。1 是丢失的数字,因为它没有出现在 nums 中。
class Solution {
public int missingNumber(int[] nums) {
int sum =0;
int numlength = nums.length;
for(int i = 0 ; i < numlength ; i++){
sum +=nums[i];
}
return numlength * (numlength + 1) / 2 - sum;
}
}class Solution {
public int missingNumber(int[] nums) {
Arrays.sort(nums);
for(int i = 0 ; i < nums.length ; i++){
if(nums[i] != i) return i;
}
return nums.length;
}
}20、两个数组的交集
给定两个数组,编写一个函数来计算它们的交集。
示例 1:
输入:nums1 = [1,2,2,1], nums2 = [2,2]
输出:[2,2]
示例 2:
输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出:[4,9]
说明:
输出结果中每个元素出现的次数,应与元素在两个数组中出现次数的最小值一致。
我们可以不考虑输出结果的顺序。
解题思路:
创建一个指针 i 指向 nums1 数组首位,指针 j 指向nums2 数组首位。
创建一个临时栈,用于存放结果集。
开始比较指针 i 和指针 j 的值大小,若两个值不等,则数字小的指针,往右移一位。
若指针 i和指针 j 的值相等,则将交集压入栈。
若 nums1 或 nums2 有一方遍历结束,代表另一方的剩余值,都是唯一存在,且不会与之产生交集的。
class Solution {
public int[] intersect(int[] nums1, int[] nums2) {
Arrays.sort(nums1);
Arrays.sort(nums2);
int length1 = nums1.length, length2 = nums2.length;
int[] intersection = new int[Math.min(length1, length2)];
int index1 = 0, index2 = 0, index = 0;
while (index1 < length1 && index2 < length2) {
if (nums1[index1] < nums2[index2]) {
index1++;
} else if (nums1[index1] > nums2[index2]) {
index2++;
} else {
intersection[index] = nums1[index1];
index1++;
index2++;
index++;
}
}
return Arrays.copyOfRange(intersection, 0, index);
}
}21、第三大的数
给你一个非空数组,返回此数组中 第三大的数 。如果不存在,则返回数组中最大的数。
示例 1:
输入:[3, 2, 1]
输出:1
解释:第三大的数是 1 。
示例 2:
输入:[1, 2]
输出:2
解释:第三大的数不存在, 所以返回最大的数 2 。
示例 3:
输入:[2, 2, 3, 1]
输出:1
解释:注意,要求返回第三大的数,是指在所有不同数字中排第三大的数。
此例中存在两个值为 2 的数,它们都排第二。在所有不同数字中排第三大的数为 1 。
提示:
1 <= nums.length <= 104
-231 <= nums[i] <= 231 - 1
进阶:你能设计一个时间复杂度 O(n) 的解决方案吗?
class Solution {
public int thirdMax(int[] nums) {
long minValue = (long)Integer.MIN_VALUE -1;
long maxFirst = minValue;
long maxSecond = minValue;
long maxThird = minValue;
for(int i = 0 ; i< nums.length ; i++){
if(nums[i] > maxFirst){
maxThird = maxSecond;
maxSecond = maxFirst;
maxFirst = nums[i];
}else if(maxSecond < nums[i] && nums[i] < maxFirst ){
maxThird = maxSecond;
maxSecond = nums[i];
}else if(maxThird < nums[i] && nums[i] < maxSecond){
maxThird = nums[i];
}
}
return (int)(maxThird == minValue ? maxFirst: maxThird);
}
}22、找到所有数组中消失的数字
给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。
示例 1:
输入:nums = [4,3,2,7,8,2,3,1]
输出:[5,6]
示例 2:
输入:nums = [1,1]
输出:[2]
提示:
n == nums.length
1 <= n <= 105
1 <= nums[i] <= n
进阶:你能在不使用额外空间且时间复杂度为 O(n) 的情况下解决这个问题吗? 你可以假定返回的数组不算在额外空间内
class Solution {
public List findDisappearedNumbers(int[] nums) {
int n = nums.length;
List result = new ArrayList<>();
for (int i = 0; i < n; i++) {
int x = (nums[i] - 1) % n; // 找到数字x存放在顺序数组中的下标
nums[x] += n;
}
for (int i = 0; i < n; i++) {
if (nums[i] <= n)
result.add(i + 1);
}
return result;
}
} 23、最小操作次数使数组元素相等
给定一个长度为 n 的 非空 整数数组,每次操作将会使 n - 1 个元素增加 1。找出让数组所有元素相等的最小操作次数。
示例:
输入:
[1,2,3]
输出:
3
解释:
只需要3次操作(注意每次操作会增加两个元素的值):
[1,2,3] => [2,3,3] => [3,4,3] => [4,4,4]
此题转换下思路就是 每个数要减多少个1 才能等于最小数
[1,2,3] 总共三次的计算方式
2 -1 = 1次
3-1 =2 次
[1,2,3,4] 总共六次的计算方式
2-1 = 1 次
3-1 = 2次
4-1 = 3次class Solution {
public int minMoves(int[] nums) {
int min=nums[0];int sum=0;
for(int n:nums){
min=min24、分发饼干
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
示例 1:
输入: g = [1,2,3], s = [1,1]
输出: 1
解释:
你有三个孩子和两块小饼干,3个孩子的胃口值分别是:1,2,3。
虽然你有两块小饼干,由于他们的尺寸都是1,你只能让胃口值是1的孩子满足。
所以你应该输出1。
示例 2:
输入: g = [1,2], s = [1,2,3]
输出: 2
解释:
你有两个孩子和三块小饼干,2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
使用贪心算法
class Solution {
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int count = 0;
int start = 0;
for(int i = 0 ; i < s.length && start < g.length; i++){
if(s[i] >= g[start]){
start ++;
count ++;
}
}
return count;
}
}25、岛屿的周长
给定一个 row x col 的二维网格地图 grid ,其中:grid[i][j] = 1 表示陆地, grid[i][j] = 0 表示水域。
网格中的格子 水平和垂直 方向相连(对角线方向不相连)。整个网格被水完全包围,但其中恰好有一个岛屿(或者说,一个或多个表示陆地的格子相连组成的岛屿)。
岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。
示例 1:
输入:grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
输出:16
解释:它的周长是上面图片中的 16 个黄色的边
示例 2:
输入:grid = [[1]]
输出:4
示例 3:
输入:grid = [[1,0]]
输出:4
grid[i][y]为 1 时 周长是4 当上下左右有陆地的话就要减1
class Solution {
public int islandPerimeter(int[][] grid) {
int sum = 0 ;
for(int i = 0 ; i < grid.length ; i++){
for(int j = 0 ; j < grid[i].length ; j++){
if(grid[i][j] == 1){
int count = 4;
if( (i - 1) >= 0 && grid[i -1][j] == 1){
count -- ;
}
if((i + 1) < grid.length && grid[i + 1][j] == 1){
count -- ;
}
if((j - 1) >= 0 && grid[i][j - 1] == 1){
count -- ;
}
if((j + 1) < grid[i].length && grid[i][j + 1] == 1){
count -- ;
}
sum += count;
}
}
}
return sum;
}
}26、最大连续1的个数
给定一个二进制数组, 计算其中最大连续 1 的个数。
示例:
输入:[1,1,0,1,1,1]
输出:3
解释:开头的两位和最后的三位都是连续 1 ,所以最大连续 1 的个数是 3.
提示:
输入的数组只包含 0 和 1 。
输入数组的长度是正整数,且不超过 10,000。
遇到1 count加1 遇到0 count清0
class Solution {
public int findMaxConsecutiveOnes(int[] nums) {
int fastIndex = 0;
int max = 0;
int count = 0;
for(int i =0 ; i < nums.length ; i++){
if(nums[i] == 1){
count ++;
max = count > max ? count : max;
}else{
count = 0;
}
}
return max;
}
}27、提莫攻击
在《英雄联盟》的世界中,有一个叫 “提莫” 的英雄,他的攻击可以让敌方英雄艾希(编者注:寒冰射手)进入中毒状态。现在,给出提莫对艾希的攻击时间序列和提莫攻击的中毒持续时间,你需要输出艾希的中毒状态总时长。
你可以认为提莫在给定的时间点进行攻击,并立即使艾希处于中毒状态。
示例1:
输入: [1,4], 2
输出: 4
原因: 第 1 秒初,提莫开始对艾希进行攻击并使其立即中毒。中毒状态会维持 2 秒钟,直到第 2 秒末结束。
第 4 秒初,提莫再次攻击艾希,使得艾希获得另外 2 秒中毒时间。
所以最终输出 4 秒。
示例2:
输入: [1,2], 2
输出: 3
原因: 第 1 秒初,提莫开始对艾希进行攻击并使其立即中毒。中毒状态会维持 2 秒钟,直到第 2 秒末结束。
但是第 2 秒初,提莫再次攻击了已经处于中毒状态的艾希。
由于中毒状态不可叠加,提莫在第 2 秒初的这次攻击会在第 3 秒末结束。
所以最终输出 3 。
class Solution {
public int findPoisonedDuration(int[] timeSeries, int duration) {
int sum = duration;
for(int i = 1 ; i < timeSeries.length ; i++){
if(timeSeries[i] - timeSeries[i -1] >= duration ){
sum +=duration;
}else{
sum +=timeSeries[i] - timeSeries[i -1];
}
}
return sum;
}
}28、键盘行
给你一个字符串数组 words ,只返回可以使用在 美式键盘 同一行的字母打印出来的单词。键盘如下图所示。
美式键盘 中:
第一行由字符 "qwertyuiop" 组成。
第二行由字符 "asdfghjkl" 组成。
第三行由字符 "zxcvbnm" 组成。
示例 1:
输入:words = ["Hello","Alaska","Dad","Peace"]
输出:["Alaska","Dad"]
示例 2:
输入:words = ["omk"]
输出:[]
示例 3:
输入:words = ["adsdf","sfd"]
输出:["adsdf","sfd"]
class Solution {
public String[] findWords(String[] words) {
String s1 = "qwertyuiop";
String s2 = "asdfghjkl";
String s3 = "zxcvbnm";
ArrayList list = new ArrayList<>();
for(String str: words){
int strLength = str.length();
int n1=0,n2=0,n3=0;
for(int i=0;i 29、 相对名次
给出 N 名运动员的成绩,找出他们的相对名次并授予前三名对应的奖牌。前三名运动员将会被分别授予 “金牌”,“银牌” 和“ 铜牌”("Gold Medal", "Silver Medal", "Bronze Medal")。
(注:分数越高的选手,排名越靠前。)
输入: [5, 4, 3, 2, 1]
输出: ["Gold Medal", "Silver Medal", "Bronze Medal", "4", "5"]
解释: 前三名运动员的成绩为前三高的,因此将会分别被授予 “金牌”,“银牌”和“铜牌” ("Gold Medal", "Silver Medal" and "Bronze Medal").
余下的两名运动员,我们只需要通过他们的成绩计算将其相对名次即可。
- N 是一个正整数并且不会超过 10000。
- 所有运动员的成绩都不相同
class Solution {
public String[] findRelativeRanks(int[] score) {
int[][] map = new int[score.length][2];
for(int i = 0; i < score.length; i++) {
map[i][0] = score[i];
map[i][1] = i;
}
Arrays.sort(map, (a, b) -> b[0] - a[0]);
String[] res = new String[score.length];
for(int i = 0; i < map.length; i++) {
if(i == 0) {
res[map[i][1]] = "Gold Medal";
} else if(i == 1) {
res[map[i][1]] = "Silver Medal";
} else if(i == 2) {
res[map[i][1]] = "Bronze Medal";
} else {
res[map[i][1]] = "" + (i + 1);
}
}
return res;
}
}30、 数组拆分1
给定长度为 2n 的整数数组 nums ,你的任务是将这些数分成 n 对, 例如 (a1, b1), (a2, b2), ..., (an, bn) ,使得从 1 到 n 的 min(ai, bi) 总和最大。
返回该 最大总和 。
示例 1:
输入:nums = [1,4,3,2]
输出:4
解释:所有可能的分法(忽略元素顺序)为:
1. (1, 4), (2, 3) -> min(1, 4) + min(2, 3) = 1 + 2 = 3
2. (1, 3), (2, 4) -> min(1, 3) + min(2, 4) = 1 + 2 = 3
3. (1, 2), (3, 4) -> min(1, 2) + min(3, 4) = 1 + 3 = 4
所以最大总和为 4
示例 2:
输入:nums = [6,2,6,5,1,2]
输出:9
解释:最优的分法为 (2, 1), (2, 5), (6, 6). min(2, 1) + min(2, 5) + min(6, 6) = 1 + 2 + 6 = 9
class Solution {
public int arrayPairSum(int[] nums) {
Arrays.sort(nums);
int sum = 0;
for(int i =0 ; i < nums.length ; i+=2){
sum+=nums[i];
}
return sum;
}
}31、 重塑矩阵
在MATLAB中,有一个非常有用的函数 reshape,它可以将一个矩阵重塑为另一个大小不同的新矩阵,但保留其原始数据。
给出一个由二维数组表示的矩阵,以及两个正整数r和c,分别表示想要的重构的矩阵的行数和列数。
重构后的矩阵需要将原始矩阵的所有元素以相同的行遍历顺序填充。
如果具有给定参数的reshape操作是可行且合理的,则输出新的重塑矩阵;否则,输出原始矩阵。
示例 1:
输入:
nums =
[[1,2],
[3,4]]
r = 1, c = 4
输出:
[[1,2,3,4]]
解释:
行遍历nums的结果是 [1,2,3,4]。新的矩阵是 1 * 4 矩阵, 用之前的元素值一行一行填充新矩阵。
示例 2:
输入:
nums =
[[1,2],
[3,4]]
r = 2, c = 4
输出:
[[1,2],
[3,4]]
解释:
没有办法将 2 * 2 矩阵转化为 2 * 4 矩阵。 所以输出原矩阵。
class Solution {
public int[][] matrixReshape(int[][] mat, int r, int c) {
if(r*c != mat.length*mat[0].length){
return mat;
}
int x=0,y=0;
int[][] reshape = new int[r][c];
for (int i = 0; i < mat.length; i++) {
for(int j = 0; j < mat[i].length; j++){
reshape[x][y] = mat[i][j];
y++;
if(y == c){
x++;
y = 0;
}
}
}
return reshape;
}
}32、 分糖果
给定一个偶数长度的数组,其中不同的数字代表着不同种类的糖果,每一个数字代表一个糖果。你需要把这些糖果平均分给一个弟弟和一个妹妹。返回妹妹可以获得的最大糖果的种类数。
示例 1:
输入: candies = [1,1,2,2,3,3]
输出: 3
解析: 一共有三种种类的糖果,每一种都有两个。
最优分配方案:妹妹获得[1,2,3],弟弟也获得[1,2,3]。这样使妹妹获得糖果的种类数最多。
示例 2 :
输入: candies = [1,1,2,3]
输出: 2
解析: 妹妹获得糖果[2,3],弟弟获得糖果[1,1],妹妹有两种不同的糖果,弟弟只有一种。这样使得妹妹可以获得的糖果种类数最多。
class Solution {
public int distributeCandies(int[] candyType) {
Set s = new HashSet();
int eachNum = candyType.length/2;
for (int i : candyType) {
s.add(i);
}
if(s.size() >= eachNum){
return eachNum;
}else{
return s.size();
}
}
} 33、 最长和谐子序列
和谐数组是指一个数组里元素的最大值和最小值之间的差别 正好是 1 。
现在,给你一个整数数组 nums ,请你在所有可能的子序列中找到最长的和谐子序列的长度。
数组的子序列是一个由数组派生出来的序列,它可以通过删除一些元素或不删除元素、且不改变其余元素的顺序而得到。
示例 1:
输入:nums = [1,3,2,2,5,2,3,7]
输出:5
解释:最长的和谐子序列是 [3,2,2,2,3]
示例 2:
输入:nums = [1,2,3,4]
输出:2
示例 3:
输入:nums = [1,1,1,1]
输出:0
使用双指针的方式
class Solution {
public int findLHS(int[] nums) {
Arrays.sort(nums);
int max = 0;
for(int i = 0 ,j = 0; i < nums.length ; i++){
while(nums[i] - nums[j] > 1){
j++;
}
if(nums[i] - nums[j] == 1){
max = Math.max(max,i-j+1);
}
}
return max;
}
}34、范围求和
给定一个初始元素全部为 0,大小为 m*n 的矩阵 M 以及在 M 上的一系列更新操作。
操作用二维数组表示,其中的每个操作用一个含有两个正整数 a 和 b 的数组表示,含义是将所有符合 0 <= i < a 以及 0 <= j < b 的元素 M[i][j] 的值都增加 1。
在执行给定的一系列操作后,你需要返回矩阵中含有最大整数的元素个数。
示例 1:
输入:
m = 3, n = 3
operations = [[2,2],[3,3]]
输出: 4
解释:
初始状态, M =
[[0, 0, 0],
[0, 0, 0],
[0, 0, 0]]
执行完操作 [2,2] 后, M =
[[1, 1, 0],
[1, 1, 0],
[0, 0, 0]]
执行完操作 [3,3] 后, M =
[[2, 2, 1],
[2, 2, 1],
[1, 1, 1]]
M 中最大的整数是 2, 而且 M 中有4个值为2的元素。因此返回 4。
此题只需要记录交集区域的右下角即可
class Solution {
public int maxCount(int m, int n, int[][] ops) {
for(int i = 0 ; i < ops.length ;i++){
m = Math.min(ops[i][0],m);
n = Math.min(ops[i][1],n);
}
return m *n ;
}
}35、两个列表的最小索引综总和
假设Andy和Doris想在晚餐时选择一家餐厅,并且他们都有一个表示最喜爱餐厅的列表,每个餐厅的名字用字符串表示。
你需要帮助他们用最少的索引和找出他们共同喜爱的餐厅。 如果答案不止一个,则输出所有答案并且不考虑顺序。 你可以假设总是存在一个答案。
示例 1:
输入:
["Shogun", "Tapioca Express", "Burger King", "KFC"]
["Piatti", "The Grill at Torrey Pines", "Hungry Hunter Steakhouse", "Shogun"]
输出: ["Shogun"]
解释: 他们唯一共同喜爱的餐厅是“Shogun”。
示例 2:
输入:
["Shogun", "Tapioca Express", "Burger King", "KFC"]
["KFC", "Shogun", "Burger King"]
输出: ["Shogun"]
解释: 他们共同喜爱且具有最小索引和的餐厅是“Shogun”,它有最小的索引和1(0+1)。
class Solution {
public String[] findRestaurant(String[] list1, String[] list2) {
List < String > res = new ArrayList < > ();
for (int sum = 0; sum < list1.length + list2.length - 1; sum++) {
for (int i = 0; i <= sum; i++) {
if (i < list1.length && sum - i < list2.length && list1[i].equals(list2[sum - i]))
res.add(list1[i]);
}
if (res.size() > 0)
break;
}
return res.toArray(new String[res.size()]);
}
}36、种花问题
假设有一个很长的花坛,一部分地块种植了花,另一部分却没有。可是,花不能种植在相邻的地块上,它们会争夺水源,两者都会死去。
给你一个整数数组 flowerbed 表示花坛,由若干 0 和 1 组成,其中 0 表示没种植花,1 表示种植了花。另有一个数 n ,能否在不打破种植规则的情况下种入 n 朵花?能则返回 true ,不能则返回 false。
示例 1:
输入:flowerbed = [1,0,0,0,1], n = 1
输出:true
示例 2:
输入:flowerbed = [1,0,0,0,1], n = 2
输出:false
class Solution {
public boolean canPlaceFlowers(int[] flowerbed, int n) {
for(int i=0;i37、 三个数的最大乘积
给你一个整型数组 nums ,在数组中找出由三个数组成的最大乘积,并输出这个乘积。
示例 1:
输入:nums = [1,2,3]
输出:6
示例 2:
输入:nums = [1,2,3,4]
输出:24
示例 3:
输入:nums = [-1,-2,-3]
输出:-6
class Solution {
public int maximumProduct(int[] nums) {
Arrays.sort(nums);
int n = nums.length;
return Math.max(nums[0] * nums[1] * nums[n - 1], nums[n - 3] * nums[n - 2] * nums[n - 1]);
}
}38、子数组最大平均数
给定 n 个整数,找出平均数最大且长度为 k 的连续子数组,并输出该最大平均数。
示例:
输入:[1,12,-5,-6,50,3], k = 4
输出:12.75
解释:最大平均数 (12-5-6+50)/4 = 51/4 = 12.75
使用滑动窗口解决
class Solution {
public double findMaxAverage(int[] nums, int k) {
double sum = 0;
for(int i = 0 ; i < k ;i ++){
sum += nums[i];
}
double max = sum;
int len = nums.length;
for(int i = k ; i < len ;i ++){
sum = sum - nums[i - k ]+nums[i];
max = Math.max(max,sum);
}
return max/k;
}
}
来源力扣(LeetCode)
链接:https://leetcode-cn.com/problems/convert-sorted-array-to-binary-search-tree